7.7: Resolver desigualdades racionales
- Page ID
- 112749
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Resolver desigualdades racionales
- Resolver una desigualdad con funciones racionales
Antes de comenzar, toma este cuestionario de preparación.
- Encuentra el valor de\(x-5\) cuando ⓐ\(x=6\) ⓑ\(x=-3\) ⓒ\(x=5\)
Si te perdiste este problema, revisa Ejemplo 1.2.16. - Resolver:\(8-2 x<12\)
Si te perdiste este problema, revisa el Ejemplo 2.6.13. - Escribe en notación de intervalos:\(-3 \leq x<5 \)
Si te perdiste este problema, revisa Ejemplo 2.6.4.
Resolver desigualdades racionales
Aprendimos a resolver desigualdades lineales después de aprender a resolver ecuaciones lineales. Las técnicas fueron muy similares con una excepción importante. Cuando multiplicamos o dividimos por un número negativo, el signo de desigualdad se invirtió.
Acabando de aprender a resolver ecuaciones racionales, ahora estamos listos para resolver las desigualdades racionales. Una desigualdad racional es una desigualdad que contiene una expresión racional.
Una desigualdad racional es una desigualdad que contiene una expresión racional.
Desigualdades como\(\quad \dfrac{3}{2 x}>1, \quad \dfrac{2 x}{x-3}<4, \quad \dfrac{2 x-3}{x-6} \geq x,\quad\) y\(\quad \dfrac{1}{4}-\dfrac{2}{x^{2}} \leq \dfrac{3}{x}\quad \) son desigualdades racionales ya que cada una contiene una expresión racional.
Cuando resolvemos una desigualdad racional, utilizaremos muchas de las técnicas que empleamos para resolver desigualdades lineales. Especialmente debemos recordar que cuando multiplicamos o dividimos por un número negativo, el signo de desigualdad debe revertirse.
Otra diferencia es que debemos considerar cuidadosamente qué valor podría hacer indefinida la expresión racional y por lo tanto hay que excluir.
Cuando resolvemos una ecuación y el resultado es\(x=3\), sabemos que hay una solución, que es 3.
Cuando resolvemos una desigualdad y el resultado es\(x>3\), sabemos que hay muchas soluciones. Graficamos el resultado para ayudar a mostrar mejor todas las soluciones, y comenzamos con 3. Tres se convierte en un punto crítico y luego decidimos si sombrear a la izquierda o a la derecha del mismo. Los números a la derecha de 3 son mayores que 3, así que sombreamos a la derecha.

Para resolver una desigualdad racional, primero debemos escribir la desigualdad con un solo cociente a la izquierda y 0 a la derecha.
A continuación determinamos los puntos críticos a utilizar para dividir la recta numérica en intervalos. Un punto crítico es un número que hace que la expresión racional sea cero o indefinida.
Luego evaluaremos los factores del numerador y denominador, y encontraremos el cociente en cada intervalo. Esto identificará el intervalo, o intervalos, que contiene todas las soluciones de la desigualdad racional.
Escribimos la solución en notación de intervalos teniendo cuidado de determinar si los puntos finales están incluidos.
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{x-1}{x+3} \geq 0\)
Solución
Paso 1. Escribe la desigualdad como un cociente a la izquierda y cero a la derecha.
Nuestra desigualdad está en esta forma. \[\dfrac{x-1}{x+3} \geq 0 \nonumber \]
Paso 2. Determinar los puntos críticos, los puntos donde la expresión racional será cero o indefinida.
La expresión racional será cero cuando el numerador sea cero. Desde\(x-1=0\) cuando\(x=1\), entonces 1 es un punto crítico.
La expresión racional quedará indefinida cuando el denominador sea cero. Desde\(x+3=0\) cuando\(x=-3\), entonces -3 es un punto crítico.
Los puntos críticos son 1 y -3.
Paso 3. Utilice los puntos críticos para dividir la recta numérica en intervalos.
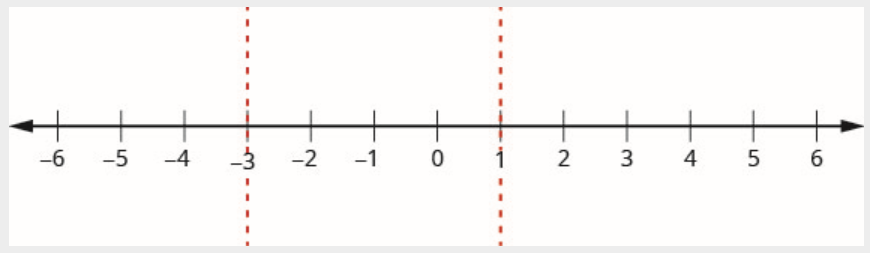
La línea numérica se divide en tres intervalos:
\[(-\infty,-3) \quad (-3,1) \quad (1,\infty) \nonumber \]
Paso 4. Probar un valor en cada intervalo. Por encima de la recta numérica se muestra el signo de cada factor de la expresión racional en cada intervalo. Debajo de la línea numérica se muestra el signo del cociente.
Para encontrar el signo de cada factor en un intervalo, elegimos cualquier punto en ese intervalo y lo usamos como punto de prueba. Cualquier punto en el intervalo le dará a la expresión el mismo signo, por lo que podemos elegir cualquier punto en el intervalo.
\[\text { Interval }(-\infty,-3) \nonumber \]
El número -4 está en el intervalo\((-\infty,-3)\). Prueba\(x=-4\) en la expresión en el numerador y el denominador.
El numerador:
\[\begin{array}{l} {x-1} \\ {-4-1} \\ {-5} \\ {\text {Negative}} \end{array} \nonumber \]
El denominador:
\[\begin{array}{l} {x+3} \\ {-4+3} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
Por encima de la recta numérica, marque el factor\(x-1\) negativo y marque el factor\(x+3\) negativo.
Dado que un negativo dividido por un negativo es positivo, marcar el cociente positivo en el intervalo\((-\infty,-3)\)
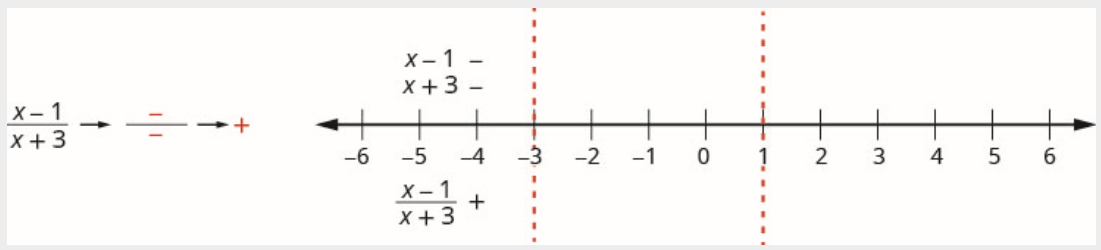
\[\text {Interval } (-3,1) \nonumber \]
El número 0 está en el intervalo\((-3,1)\). Prueba\(x=0\).
El numerador:
\[\begin{array}{l} {x-1} \\ {0-1} \\ {-1} \\ {\text {Negative}} \end{array} \nonumber \]
El denominador:
\[\begin{array}{l} {x+3} \\ {0+3} \\ {3} \\ {\text {Positive}} \end{array} \nonumber \]
Por encima de la recta numérica, marque el factor\(x-1\) negativo y marque\(x+3\) positivo.
Dado que un negativo dividido por un positivo es negativo, el cociente se marca negativo en el intervalo\((-3,1)\).
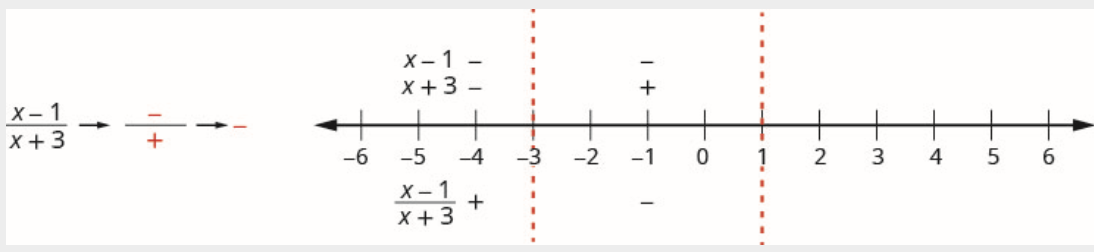
\[\text {Interval }(1, \infty) \nonumber \]
El número 2 está en el intervalo\((1, \infty)\). Prueba\(x=2\).
El numerador:
\[\begin{array}{l} {x-1} \\ {2-1} \\ {1} \\ {\text {Positive}} \end{array} \nonumber \]
El denominador:
\[\begin{array}{l} {x+3} \\ {2+3} \\ {5} \\ {\text {Positive}} \end{array} \nonumber \]
Por encima de la recta numérica, marque el factor\(x-1\) positivo y marque\(x+3\) positivo.
Dado que un positivo dividido por un positivo es positivo, marcar el cociente positivo en el intervalo\((1, \infty)\).
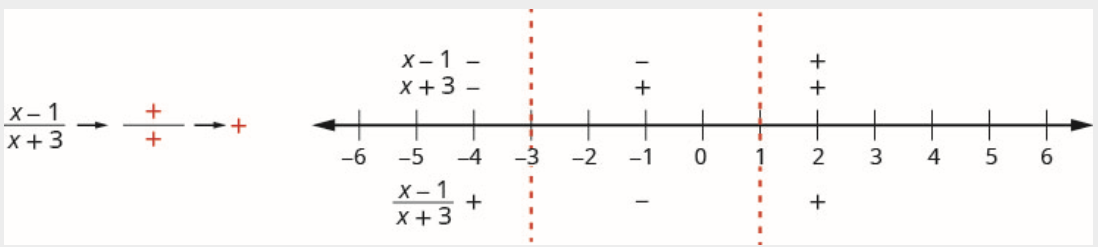
Paso 5. Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.
Queremos que el cociente sea mayor o igual a cero, por lo que los números en los intervalos\((-\infty,-3)\) y\((1, \infty) \) son soluciones.
Pero ¿qué pasa con los puntos críticos?
El punto crítico\(x=-3\) hace que el denominador sea 0, por lo que debe ser excluido de la solución y lo marcamos con un paréntesis.
El punto crítico\(x=1\) hace que toda la expresión racional sea 0. La desigualdad requiere que la expresión racional sea mayor o igual a. Entonces, 1 es parte de la solución y lo marcaremos con un soporte.
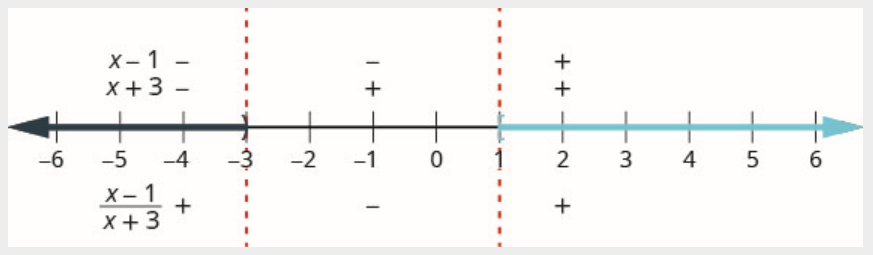
Recordemos que cuando tenemos una solución conformada por más de un intervalo utilizamos el símbolo de unión,\(\cup \), para conectar los dos intervalos. La solución en notación de intervalos es\((-\infty,-3) \cup[1, \infty)\).
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{x-2}{x+4} \geq 0\)
- Contestar
-
\((-\infty,-4) \cup[2, \infty)\)
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{x+2}{x-4} \geq 0\)
- Contestar
-
\((-\infty,-2] \cup(4, \infty)\)
Resumimos los pasos para una fácil referencia.
Paso 1. Escribe la desigualdad como un cociente a la izquierda y cero a la derecha.
Paso 2. Determinar los puntos críticos, los puntos donde la expresión racional será cero o indefinida.
Paso 3. Utilice los puntos críticos para dividir la recta numérica en intervalos.
Paso 4. Probar un valor en cada intervalo. Encima de la recta numérica muestran el signo de cada factor del numerador y denominador en cada intervalo. Debajo de la línea numérica se muestra el signo del cociente.
Paso 5. Determinar los intervalos donde la desigualdad es correcta. Escribe la solución en notación de intervalos.
El siguiente ejemplo requiere que primero obtengamos la desigualdad racional en la forma correcta.
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{4 x}{x-6}<1\)
Solución
\[\dfrac{4 x}{x-6}<1 \nonumber \]
Resta 1 para obtener cero a la derecha.
\[\dfrac{4 x}{x-6}-1<0 \nonumber \]
Reescribe 1 como una fracción usando la pantalla LCD.
\[\dfrac{4 x}{x-6}-\frac{x-6}{x-6}<0 \nonumber \]
Restar los numeradores y colocar la diferencia sobre el denominador común.
\[\dfrac{4 x-(x-6)}{x-6}<0 \nonumber \]
Simplificar.
\[\dfrac{3 x+6}{x-6}<0 \nonumber \]
Facturar el numerador para mostrar todos los factores.
\[\dfrac{3(x+2)}{x-6}<0 \nonumber \]
Encuentra los puntos críticos.
El cociente será cero cuando el numerador sea cero. El cociente es indefinido cuando el denominador es cero.
\[\begin{array}{rlrl} {x+2} & {=0} & {x-6} & {=0} \\ {x} & {=-2} & {x} & {=6} \end{array} \nonumber \]
Utilice los puntos críticos para dividir la recta numérica en intervalos.
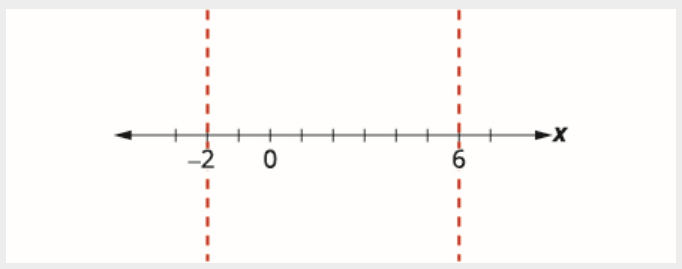
Probar un valor en cada intervalo.
| \((-\infty,-2)\) | \((-2,6)\) | \((6, \infty)\) | |
|---|---|---|---|
| \(x+2)\) | \ ((-\ infty, -2)\)” style="vertical-align:middle;” class="lt-math-5164">
x+2 -3+2 -1 - |
\ ((-2,6)\)” style="vertical-align:middle;” class="lt-math-5164">
x+2 0+2 2 + |
\ ((6,\ infty)\)” style="vertical-align:middle;” class="lt-math-5164">
x+2 7+2 9 + |
| \(x-6\) | \ ((-\ infty, -2)\)” style="vertical-align:middle;” class="lt-math-5164">
x-6 -3-6 -9 - |
\ ((-2,6)\)” style="vertical-align:middle;” class="lt-math-5164">
x-6 0-6 -6 - |
\ ((6,\ infty)\)” style="vertical-align:middle;” class="lt-math-5164">
x-6 7-6 1 + |
Por encima de la recta numérica se muestra el signo de cada factor de la expresión racional en cada intervalo. Debajo de la línea numérica se muestra el signo del cociente.
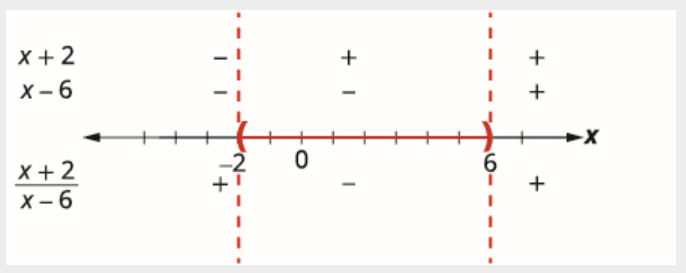
Determinar los intervalos donde la desigualdad es correcta. Queremos que el cociente sea negativo, por lo que la solución incluye los puntos entre −2 y 6. Dado que la desigualdad es estrictamente menor que, no se incluyen los puntos finales.
Escribimos la solución en notación de intervalos como (−2, 6).
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{3 x}{x-3}<1\).
- Contestar
-
\(\left(-\dfrac{3}{2}, 3\right)\)
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{3 x}{x-4}<2\).
- Contestar
-
\((-8,4)\)
En el siguiente ejemplo, el numerador siempre es positivo, por lo que el signo de la expresión racional depende del signo del denominador.
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{5}{x^{2}-2 x-15}>0\).
Solución
La desigualdad está en la forma correcta.
\[\dfrac{5}{x^{2}-2 x-15}>0 \nonumber \]
Facturar el denominador.
\[\dfrac{5}{(x+3)(x-5)}>0 \nonumber \]
Encuentra los puntos críticos. El cociente es 0 cuando el numerador es 0. Dado que el numerador es siempre 5, el cociente no puede ser 0.
El cociente quedará indefinido cuando el denominador sea cero.
\[\begin{aligned} &(x+3)(x-5)=0\\ &x=-3, x=5 \end{aligned} \nonumber \]
Utilice los puntos críticos para dividir la recta numérica en intervalos.
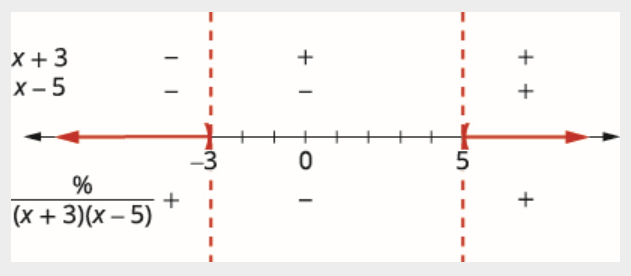
Valores de prueba en cada intervalo. Encima de la recta numérica muestran el signo de cada factor del denominador en cada intervalo. Debajo de la recta numérica, mostrar el signo del cociente.
Escribe la solución en notación de intervalos.
\[(-\infty,-3) \cup(5, \infty) \nonumber \]
Solve and write the solution in interval notation: \(\dfrac{1}{x^{2}+2 x-8}>0\).
- Answer
-
\((-\infty,-4) \cup(2, \infty)\)
Solve and write the solution in interval notation: \(\dfrac{3}{x^{2}+x-12}>0 \).
- Answer
-
\((-\infty,-4) \cup(3, \infty)\)
The next example requires some work to get it into the needed form.
Solve and write the solution in interval notation: \(\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x}\).
Solution
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}<\dfrac{5}{3 x} \nonumber \]
Subtract \(\dfrac{5}{3 x}\) to get zero on the right.
\[\dfrac{1}{3}-\dfrac{2}{x^{2}}-\dfrac{5}{3 x}<0 \nonumber \]
Rewrite to get each fraction with the LCD
\[\dfrac{1 \cdot x^{2}}{3 \cdot x^{2}}-\dfrac{2 \cdot 3}{x^{2} \cdot 3}-\dfrac{5 \cdot x}{3 x-x}<0 \nonumber \]
Simplify.
\[\dfrac{x^{2}}{3 x^{2}}-\dfrac{6}{3 x^{2}}-\dfrac{5 x}{3 x^{2}}<0 \nonumber \]
Subtract the numerators and place the difference over the common denominator.
\[\dfrac{x^{2}-5 x-6}{3 x^{2}}<0 \nonumber \]
Factor the numerator.
\[\dfrac{(x-6)(x+1)}{3 x^{2}}<0 \nonumber \]
Find the critical points.
\[\begin{array}{rlrl} {3 x^{2}=0} && {x-6=0} && {x+1=0} \\ {x=0} && {x=6} && {x=-1} \end{array} \nonumber \]
Use the critical points to divide the number line into intervals.
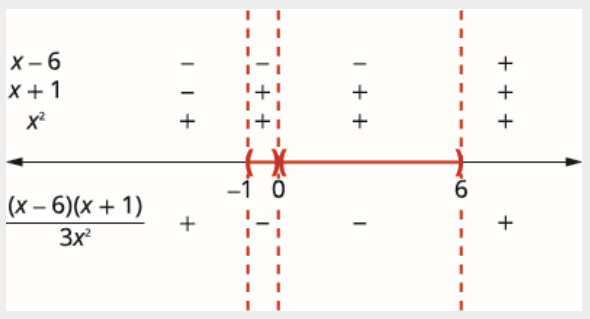
Por encima de la recta numérica se muestra el signo de cada factor en cada intervalo. Debajo de la recta numérica, mostrar el signo del cociente.
Ya que, se excluye 0, la solución son los dos\((-1,0) \cup(0,6)\) intervalos,\((-1,0)\) y\((0,6)\).
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{1}{2}+\dfrac{4}{x^{2}}<\dfrac{3}{x}\).
- Contestar
-
\((2,4)\)
Resuelve y escribe la solución en notación de intervalos:\(\dfrac{1}{3}+\dfrac{6}{x^{2}}<\dfrac{3}{x}\).
- Contestar
-
\((3,6)\)
Resolver una desigualdad con funciones racionales
Cuando se trabaja con funciones racionales, a veces es útil saber cuándo la función es mayor o menor que un valor particular. Esto lleva a una desigualdad racional.
Dada la función\(R(x)=\dfrac{x+3}{x-5}\), encuentra los valores de x que hacen que la función sea menor o igual a 0.
Solución
Queremos que la función sea menor o igual a 0.
\[R(x) \leq 0 \nonumber \]
Sustituir la expresión racional por\(R(x)\).
\[\dfrac{x+3}{x-5} \leq 0 \quad x \neq 5 \nonumber \]
Encuentra los puntos críticos.
\[\begin{array}{rlrl} {x+3=0} && {x-5=0} \\ {x=-3} && {x=5} \end{array} \nonumber \]
Utilice los puntos críticos para dividir la recta numérica en intervalos.
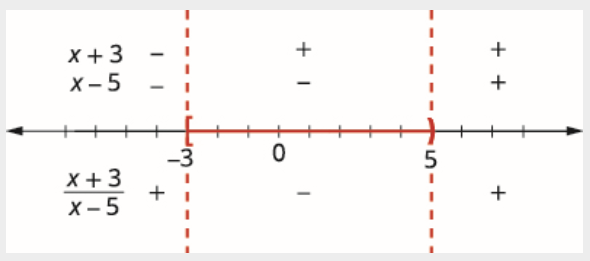
Valores de prueba en cada intervalo. Por encima de la recta numérica, mostrar el signo de cada factor en cada intervalo. Debajo de la recta numérica, mostrar el signo del cociente. Escribe la solución en notación de intervalos. Ya que 5 está excluido nosotros, no lo incluimos en el intervalo.
\[[-3,5) \nonumber \]
Given the function \(R(x)=\dfrac{x-2}{x+4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\((-4,2]\)
Given the function \(R(x)=\dfrac{x+1}{x-4}\), find the values of \(x\) that make the function less than or equal to 0.
- Answer
-
\([-1,4)\)
In economics, the function \(C(x)\) is used to represent the cost of producing \(x\) units of a commodity. The average cost per unit can be found by dividing \(C(x)\) by the number of items \(x\). Then, the average cost per unit is \(c(x)=\dfrac{C(x)}{x}).
The function\(C(x)=10 x+3000\) represents the cost to produce \(x\), number of items. Find:
- The average cost function, \(c(x)\)
- How many items should be produced so that the average cost is less than $40.
Solution
- \[C(x)=10 x+3000 \nonumber \]
The average cost function is \(c(x)=\dfrac{C(x)}{x})\). To find the average cost function, divide the cost function by \(x\).
\[\begin{aligned} &c(x)=\dfrac{C(x)}{x}\\ &c(x)=\dfrac{10 x+3000}{x} \end{aligned} \nonumber \]
The average cost function is \(c(x)=\dfrac{10 x+3000}{x} \)
- We want the function \(c(x)\) to be less than 40.
\[c(x)<40 \nonumber \]
Substitute the rational expression forc(x).
\[\dfrac{10 x+3000}{x}<40, \quad x \neq 0 \nonumber \]
Subtract 40 to get 0 on the right.
\[\dfrac{10 x+3000}{x}-40<0 \nonumber \]
Rewrite the left side as one quotient by finding the LCD and performing the subtraction.
\[\begin{aligned} \dfrac{10 x+3000}{x}-40\left(\dfrac{x}{x}\right) &<0\\ \dfrac{10 x+3000}{x}-\dfrac{40 x}{x} &<0\\ \dfrac{10 x+3000-40 x}{x} &<0 \\ \dfrac{-30 x+3000}{x} &<0 \end{aligned} \nonumber \]
Factor the numerator to show all factors.
\[\begin{array}{ll} {\dfrac{-30(x-100)}{x}<0} \\ {-30(x-100)=0} && {x=0} \end{array} \nonumber \]
Find the critical points.
\[\begin{array}{rl} {-30 \neq 0} & {x-100=0} \\ &{x=100} \end{array} \nonumber \]
More than 100 items must be produced to keep the average cost below $40 per item.
The function\(C(x)=20 x+6000\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $60.
- Answer
-
- \(c(x)=\dfrac{20 x+6000}{x}\)
- More than 150 items must be produced to keep the average cost below $60 per item.
The function\(C(x)=5 x+900\) represents the cost to produce \(x\), number of items. Find:
- How many items should be produced so that the average cost is less than $20.
- Answer
-
- \(c(x)=\dfrac{5 x+900}{x}\)
- More than 60 items must be produced to keep the average cost below $20 per item.


