8.2: Simplificar expresiones con raíces
- Page ID
- 112511
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Simplifica expresiones con raíces
- Estimar y aproximar raíces
- Simplificar expresiones variables con raíces
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar: a.\((−9)^{2}\) b.\(-9^{2}\) c.\((−9)^{3}\)
Si te perdiste este problema, revisa el Ejemplo 2.21. - Redondear\(3.846\) a la centésima más cercana.
Si te perdiste este problema, revisa el Ejemplo 1.34. - Simplificar: a.\(x^{3} \cdot x^{3}\) b.\(y^{2} \cdot y^{2} \cdot y^{2}\) c.\(z^{3} \cdot z^{3} \cdot z^{3} \cdot z^{3}\)
Si te perdiste este problema, revisa el Ejemplo 5.12.
Simplificar expresiones con raíces
En Fundaciones, nos fijamos brevemente en las raíces cuadradas. Recuerda que cuando un número real\(n\) se multiplica por sí mismo, lo escribimos\(n^{2}\) y leemos 'al\(n^{2}\) cuadrado'. Este número se llama el cuadrado de\(n\), y\(n\) se llama la raíz cuadrada. Por ejemplo,
\(13^{2}\)se lee "\(13\)cuadrado”
\(169\)se llama el cuadrado de\(13\), ya que\(13^{2}=169\)
\(13\)es una raíz cuadrada de\(169\)
Cuadrado
Si\(n^{2}=m\), entonces\(m\) es el cuadrado de\(n\).
Raíz cuadrada
Si\(n^{2}=m\), entonces\(n\) es una raíz cuadrada de\(m\).
Observe\((−13)^{2} = 169\) también, por lo que también\(−13\) es una raíz cuadrada de\(169\). Por lo tanto, ambos\(13\) y\(−13\) son raíces cuadradas de\(169\).
Entonces, cada número positivo tiene dos raíces cuadradas, una positiva y otra negativa. ¿Y si solo quisiéramos la raíz cuadrada positiva de un número positivo? Usamos un signo radical, y escribimos,\(\sqrt{m}\), que denota la raíz cuadrada positiva de\(m\). La raíz cuadrada positiva también se llama raíz cuadrada principal.
También utilizamos el signo radical para la raíz cuadrada de cero. Porque\(0^{2}=0, \sqrt{0}=0\). Observe que cero tiene solo una raíz cuadrada.
\(\sqrt{m}\)se lee “la raíz cuadrada de\(m\).”
Si\(n^{2}=m\), entonces\(n=\sqrt{m}\), para\(n\geq 0\).
Sabemos que cada número positivo tiene dos raíces cuadradas y el signo radical indica el positivo. Escribimos\(\sqrt{169}=13\). Si queremos encontrar la raíz cuadrada negativa de un número, colocamos un negativo frente al signo radical. Por ejemplo,\(-\sqrt{169}=-13\).
Simplificar:
- \(\sqrt{144}\)
- \(-\sqrt{289}\)
Solución:
a.
\(\sqrt{144}\)
Ya que\(12^{2}=144\).
\(12\)
b.
\(-\sqrt{289}\)
Desde\(17^{2}=289\) y lo negativo está frente al signo radical.
\(-17\)
Simplificar:
- \(-\sqrt{64}\)
- \(\sqrt{225}\)
- Responder
-
- \(-8\)
- \(15\)
Simplificar:
- \(\sqrt{100}\)
- \(-\sqrt{121}\)
- Responder
-
- \(10\)
- \(-11\)
¿Podemos simplificar\(-\sqrt{49}\)? ¿Hay un número cuyo cuadrado es\(-49\)?
\((\)___\( )^{2}=-49\)
Cualquier número positivo al cuadrado es positivo. Cualquier número negativo al cuadrado es positivo. No hay un número real igual a\(\sqrt{-49}\). La raíz cuadrada de un número negativo no es un número real.
Simplificar:
- \(\sqrt{-196}\)
- \(-\sqrt{64}\)
Solución:
a.
\(\sqrt{-196}\)
No hay un número real cuyo cuadrado sea\(-196\).
\(\sqrt{-196}\)no es un número real.
b.
\(-\sqrt{64}\)
El negativo está frente al radical.
\(-8\)
Simplificar:
- \(\sqrt{-169}\)
- \(-\sqrt{81}\)
- Responder
-
- no es un número real
- \(-9\)
Simplificar:
- \(-\sqrt{49}\)
- \(\sqrt{-121}\)
- Responder
-
- \(-7\)
- no es un número real
Hasta el momento sólo hemos hablado de cuadrados y raíces cuadradas. Extendamos ahora nuestro trabajo para incluir poderes superiores y raíces superiores.
Revisemos un poco de vocabulario primero.
\(\begin{array}{ll}{\text { We write: }} & {\text { We say: }} \\ {n^{2}} & {n \text { squared }} \\ {n^{3}} & {n \text { cubed }} \\ {n^{4}} & {n \text { to the fourth power }} \\ {n^{5}} & {n \text { to the fifth power }}\end{array}\)
Los términos 'cuadrado' y 'cubo' provienen de las fórmulas para área de un cuadrado y volumen de un cubo.
Será útil tener una tabla de los poderes de los enteros desde\(−5\) hasta\(5\). Ver Figura 8.1.2
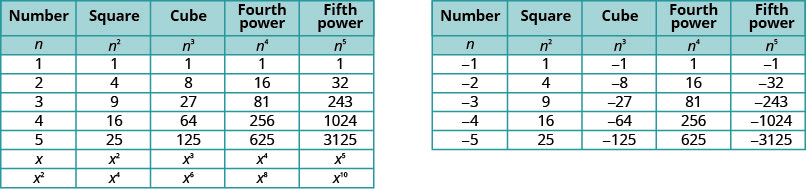
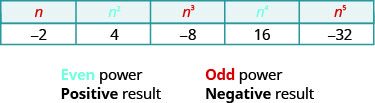
Observe los letreros en la tabla. Todos los poderes de los números positivos son positivos, claro. Pero cuando tenemos un número negativo, los poderes pares son positivos y los impares son negativos. Copiaremos la fila con los poderes de\(−2\) para ayudarte a ver esto.
Ahora extenderemos la definición de raíz cuadrada a raíces superiores.
Si\(b^{n}=a\), entonces\(b\) es una\(n^{th}\) raíz de\(a\).
La\(n^{th}\) raíz principal de\(a\) está escrita\(\sqrt[n]{a}\).
El\(n\) se llama el índice del radical.
Al igual que usamos la palabra 'cubos' para\(b^{3}\), usamos el término 'raíz cúbica' para\(\sqrt[3]{a}\).
Podemos referirnos a la Figura 8.1.2 para ayudar a encontrar raíces superiores.
\(\begin{aligned} 4^{3} &=64 & \sqrt[3]{64}&=4 \\ 3^{4} &=81 & \sqrt[4]{81}&=3 \\(-2)^{5} &=-32 & \sqrt[5]{-32}&=-2 \end{aligned}\)
¿Podríamos tener una raíz par de un número negativo? Sabemos que la raíz cuadrada de un número negativo no es un número real. Lo mismo es cierto para cualquier raíz par. Incluso las raíces de los números negativos no son números reales. Las raíces impares de números negativos son números reales.
Propiedades de\(\sqrt[n]{a}\)
Cuando\(n\) es un número par y
- \(a \geq 0\), entonces\(\sqrt[n]{a}\) es un número real.
- \(a<0\), entonces no\(\sqrt[n]{a}\) es un número real.
Cuando\(n\) es un número impar,\(\sqrt[n]{a}\) es un número real para todos los valores de\(a\).
Aplicaremos estas propiedades en los siguientes dos ejemplos.
Simplificar:
- \(\sqrt[3]{64}\)
- \(\sqrt[4]{81}\)
- \(\sqrt[5]{32}\)
Solución:
a.
\(\sqrt[3]{64}\)
Ya que\(4^{3}=64\).
\(4\)
b.
\(\sqrt[4]{81}\)
Ya que\((3)^{4}=81\).
\(3\)
c.
\(\sqrt[5]{32}\)
Ya que\((2)^{5}=32\).
\(2\)
Simplificar:
- \(\sqrt[3]{27}\)
- \(\sqrt[4]{256}\)
- \(\sqrt[5]{243}\)
- Responder
-
- \(3\)
- \(4\)
- \(3\)
Simplificar:
- \(\sqrt[3]{1000}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{243}\)
- Responder
-
- \(10\)
- \(2\)
- \(3\)
En este ejemplo estar alerta de los signos negativos así como de los poderes pares e impares.
Simplificar:
- \(\sqrt[3]{-125}\)
- \(\sqrt[4]{16}\)
- \(\sqrt[5]{-243}\)
Solución:
a.
\(\sqrt[3]{-125}\)
Ya que\((-5)^{3}=-125\).
\(-5\)
b.
\(\sqrt[4]{16}\)
Piensa,\((?)^{4}=-16\). Ningún número real elevado a la cuarta potencia es negativo.
No es un número real.
c.
\(\sqrt[5]{-243}\)
Ya que\((-3)^{5}=-243\).
\(-3\)
Simplificar:
- \(\sqrt[3]{-27}\)
- \(\sqrt[4]{-256}\)
- \(\sqrt[5]{-32}\)
- Responder
-
- \(-3\)
- no real
- \(-2\)
Simplificar:
- \(\sqrt[3]{-216}\)
- \(\sqrt[4]{-81}\)
- \(\sqrt[5]{-1024}\)
- Responder
-
- \(-6\)
- no real
- \(-4\)
Estimación y Aproximación de Raíces
Cuando vemos un número con un signo radical, muchas veces no pensamos en su valor numérico. Si bien probablemente sabemos que el\(\sqrt{4}=2\), ¿cuál es el valor de\(\sqrt{21}\) o\(\sqrt[3]{50}\)? En algunas situaciones una estimación rápida es significativa y en otras es conveniente tener una aproximación decimal.
Para obtener una estimación numérica de una raíz cuadrada, buscamos números cuadrados perfectos más cercanos al radicando. Para encontrar una estimación de\(\sqrt{11}\), vemos\(11\) es entre números cuadrados perfectos\(9\) y\(16\), más cerca de\(9\). Su raíz cuadrada entonces estará entre\(3\) y\(4\), pero más cerca de\(3\).
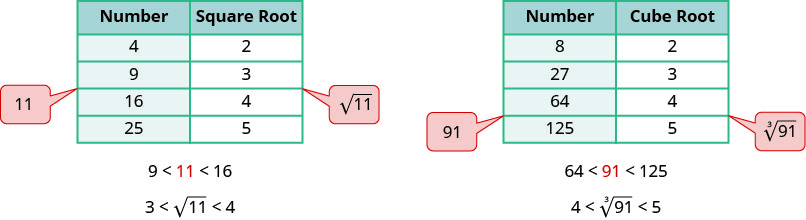
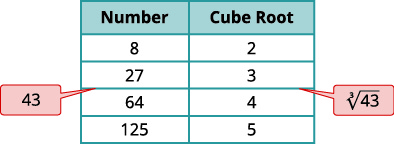
De igual manera, para estimar\(\sqrt[3]{91}\), vemos\(91\) es entre números de cubo perfectos\(64\) y\(125\). La raíz cubo entonces estará entre\(4\) y\(5\).
Estimar cada raíz entre dos números enteros consecutivos:
- \(\sqrt{105}\)
- \(\sqrt[3]{43}\)
Solución:
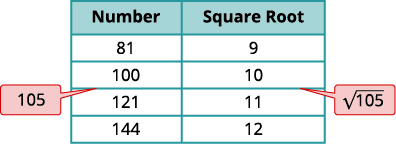
a. Piense en los números cuadrados perfectos más cercanos a\(105\). Haz una mesita de estos cuadrados perfectos y sus raíces cuadradas.
| \(\sqrt{105}\) | |
 |
|
| Localizar\(105\) entre dos cuadrados perfectos consecutivos. | \(100<\color{red}105 \color{black} <121\) |
| \(\sqrt{105}\)está entre sus raíces cuadradas. | \(10< \color{red}\sqrt{105}< \color{black}11\) |
b. de manera similar ubicamos\(43\) entre dos números de cubo perfectos.
| \(\sqrt[3]{43}\) | |
 |
|
| Localiza\(43\) entre dos cubos perfectos consecutivos. |  |
| \(\sqrt[3]{43}\)está entre sus raíces cubicas. |  |
Estimar cada raíz entre dos números enteros consecutivos:
- \(\sqrt{38}\)
- \(\sqrt[3]{93}\)
- Responder
-
- \(6<\sqrt{38}<7\)
- \(4<\sqrt[3]{93}<5\)
Estimar cada raíz entre dos números enteros consecutivos:
- \(\sqrt{84}\)
- \(\sqrt[3]{152}\)
- Responder
-
- \(9<\sqrt{84}<10\)
- \(5<\sqrt[3]{152}<6\)
Existen métodos matemáticos para aproximar raíces cuadradas, pero hoy en día la mayoría de la gente usa una calculadora para encontrar raíces cuadradas. Para encontrar una raíz cuadrada utilizará la\(\sqrt{x}\) clave en su calculadora. Para encontrar una raíz cúbica, o cualquier raíz con un índice más alto, utilizará la\(\sqrt[y]{x}\) clave.
Cuando usas estas claves, obtienes un valor aproximado. Se trata de una aproximación, precisa al número de dígitos que se muestran en la pantalla de tu calculadora. El símbolo para una aproximación es\(≈\) y se lee 'aproximadamente'.
Supongamos que su calculadora tiene una pantalla de\(10\) dígitos. Verías que
\(\sqrt{5} \approx 2.236067978\)redondeado a dos decimales es\(\sqrt{5} \approx 2.24\)
\(\sqrt[4]{93} \approx 3.105422799\)redondeado a dos decimales es\(\sqrt[4]{93} \approx 3.11\)
¿Cómo sabemos que estos valores son aproximaciones y no los valores exactos? Mira lo que sucede cuando los cuadramos:
\(\begin{aligned}(2.236067978)^{2} &=5.000000002 &(3.105422799)^{4}&=92.999999991 \\(2.24)^{2} &=5.0176 & (3.11)^{4}&=93.54951841 \end{aligned}\)
Sus cuadrados están cerca\(5\), pero no son exactamente iguales a\(5\). Los cuartos poderes son cercanos\(93\), pero no iguales a\(93\).
Redondear a dos decimales:
- \(\sqrt{17}\)
- \(\sqrt[3]{49}\)
- \(\sqrt[4]{51}\)
Solución:
a.
\(\sqrt{17}\)
Utilice la clave de raíz cuadrada de la calculadora.
\(4.123105626 \dots\)
Redondear a dos decimales.
\(4.12\)
\(\sqrt{17} \approx 4.12\)
b.
\(\sqrt[3]{49}\)
Utilice la\(\sqrt[y]{x}\) clave de la calculadora.
\(3.659305710 \ldots\)
Redondear a dos decimales.
\(3.66\)
\(\sqrt[3]{49} \approx 3.66\)
c.
\(\sqrt[4]{51}\)
Utilice la\(\sqrt[y]{x}\) clave de la calculadora.
\(2.6723451177 \ldots\)
Redondear a dos decimales.
\(2.67\)
\(\sqrt[4]{51} \approx 2.67\)
Redondear a dos decimales:
- \(\sqrt{11}\)
- \(\sqrt[3]{71}\)
- \(\sqrt[4]{127}\)
- Responder
-
- \(\approx 3.32\)
- \(\approx 4.14\)
- \(\approx 3.36\)
Redondear a dos decimales:
- \(\sqrt{13}\)
- \(\sqrt[3]{84}\)
- \(\sqrt[4]{98}\)
- Responder
-
- \(\approx 3.61\)
- \(\approx 4.38\)
- \(\approx 3.15\)
Simplificar expresiones variables con raíces
La raíz impar de un número puede ser positiva o negativa. Por ejemplo,
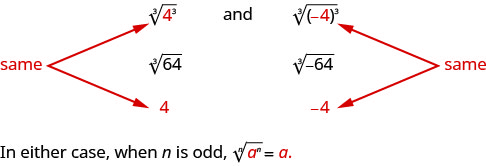
Pero, ¿qué pasa con una raíz par? Queremos la raíz principal, entonces\(\sqrt[4]{625}=5\).
Pero fíjate,
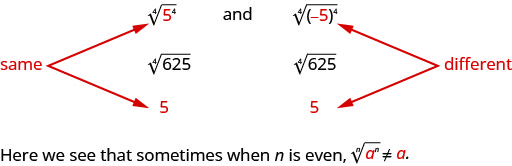
¿Cómo podemos asegurarnos de que sea la cuarta raíz de\(−5\) elevado a la cuarta potencia\(5\)? Podemos usar el valor absoluto. \(|−5|=5\). Entonces decimos que cuando\(n\) es parejo\(\sqrt[n]{a^{n}}=|a|\). Esto garantiza que la raíz principal sea positiva.
Para cualquier entero\(n\geq 2\),
cuando el índice\(n\) es impar\(\sqrt[n]{a^{n}}=a\)
cuando el índice\(n\) es par\(\sqrt[n]{a^{n}}=|a|\)
Debemos usar los signos de valor absoluto cuando tomamos una raíz par de una expresión con una variable en el radical.
Simplificar:
- \(\sqrt{x^{2}}\)
- \(\sqrt[3]{n^{3}}\)
- \(\sqrt[4]{p^{4}}\)
- \(\sqrt[5]{y^{5}}\)
Solución:
a. Utilizamos el valor absoluto para asegurarnos de obtener la raíz positiva.
\(\sqrt{x^{2}}\)
Dado que el índice\(n\) es parejo,\(\sqrt[n]{a^{n}}=|a|\).
b. Esta es una raíz impar indexada por lo que no hay necesidad de un signo de valor absoluto.
\(\sqrt[3]{m^{3}}\)
Dado que el índice\(n\) es impar,\(\sqrt[n]{a^{n}}=a\).
\(m\)
c.
\(\sqrt[4]{p^{4}}\)
Ya que el índice\(n\) es parejo\(\sqrt[n]{a^{n}}=|a|\).
\(|p|\)
d.
\(\sqrt[5]{y^{5}}\)
Dado que el índice\(n\) es impar,\(\sqrt[n]{a^{n}}=a\).
\(y\)
Simplificar:
- \(\sqrt{b^{2}}\)
- \(\sqrt[3]{w^{3}}\)
- \(\sqrt[4]{m^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- Responder
-
- \(|b|\)
- \(w\)
- \(|m|\)
- \(q\)
Simplificar:
- \(\sqrt{y^{2}}\)
- \(\sqrt[3]{p^{3}}\)
- \(\sqrt[4]{z^{4}}\)
- \(\sqrt[5]{q^{5}}\)
- Responder
-
- \(|y|\)
- \(p\)
- \(|z|\)
- \(q\)
¿Qué pasa con las raíces cuadradas de las potencias superiores de las variables? Dice la Propiedad de Poder de los Exponentes\(\left(a^{m}\right)^{n}=a^{m \cdot n}\). Entonces, si cuadramos\(a^{m}\), el exponente se convertirá\(2m\).
\(\left(a^{m}\right)^{2}=a^{2 m}\)
Mirando ahora a la raíz cuadrada.
\(\sqrt{a^{2 m}}\)
Ya que\(\left(a^{m}\right)^{2}=a^{2 m}\).
\(\sqrt{\left(a^{m}\right)^{2}}\)
Ya que\(n\) es parejo\(\sqrt[n]{a^{n}}=|a|\).
\(\left|a^{m}\right|\)
Entonces\(\sqrt{a^{2 m}}=\left|a^{m}\right|\).
Aplicamos este concepto en el siguiente ejemplo.
Simplificar:
- \(\sqrt{x^{6}}\)
- \(\sqrt{y^{16}}\)
Solución:
a.
\(\sqrt{x^{6}}\)
Ya que\(\left(x^{3}\right)^{2}=x^{6}\).
\(\sqrt{\left(x^{3}\right)^{2}}\)
Ya que el índice\(n\) es parejo\(\sqrt{a^{n}}=|a|\).
\(\left|x^{3}\right|\)
b.
\(\sqrt{y^{16}}\)
Ya que\(\left(y^{8}\right)^{2}=y^{16}\).
\(\sqrt{\left(y^{8}\right)^{2}}\)
Ya que el índice\(n\) es parejo\(\sqrt[n]{a^{n}}=|a|\).
\(y^{8}\)
En este caso no se necesita el signo de valor absoluto ya que\(y^{8}\) es positivo.
Simplificar:
- \(\sqrt{y^{18}}\)
- \(\sqrt{z^{12}}\)
- Responder
-
- \(|y^{9}|\)
- \(z^{6}\)
Simplificar:
- \(\sqrt{m^{4}}\)
- \(\sqrt{b^{10}}\)
- Responder
-
- \(m^{2}\)
- \(|b^{5}|\)
El siguiente ejemplo utiliza la misma idea para raíces superiores.
Simplificar:
- \(\sqrt[3]{y^{18}}\)
- \(\sqrt[4]{z^{8}}\)
Solución:
a.
\(\sqrt[3]{y^{18}}\)
Ya que\(\left(y^{6}\right)^{3}=y^{18}\).
\(\sqrt[3]{\left(y^{6}\right)^{3}}\)
Ya que\(n\) es impar,\(\sqrt[n]{a^{n}}=a\).
\(y^{6}\)
b.
\(\sqrt[4]{z^{8}}\)
Ya que\(\left(z^{2}\right)^{4}=z^{8}\).
\(\sqrt[4]{\left(z^{2}\right)^{4}}\)
Ya que\(z^{2}\) es positivo, no necesitamos un signo de valor absoluto.
\(z^{2}\)
Simplificar:
- \(\sqrt[4]{u^{12}}\)
- \(\sqrt[3]{v^{15}}\)
- Responder
-
- \(|u^{3}|\)
- \(v^{5}\)
Simplificar:
- \(\sqrt[5]{c^{20}}\)
- \(\sqrt[6]{d^{24}}\)
- Responder
-
- \(c^{4}\)
- \(d^{4}\)
En el siguiente ejemplo, ahora tenemos un coeficiente frente a la variable. El concepto\(\sqrt{a^{2 m}}=\left|a^{m}\right|\) funciona de la misma manera.
\(\sqrt{16 r^{22}}=4\left|r^{11}\right|\)porque\(\left(4 r^{11}\right)^{2}=16 r^{22}\).
Pero aviso\(\sqrt{25 u^{8}}=5 u^{4}\) y no se necesita signo de valor absoluto como siempre\(u^{4}\) es positivo.
Simplificar:
- \(\sqrt{16 n^{2}}\)
- \(-\sqrt{81 c^{2}}\)
Solución:
a.
\(\sqrt{16 n^{2}}\)
Ya que\((4 n)^{2}=16 n^{2}\).
\(\sqrt{(4 n)^{2}}\)
Ya que el índice\(n\) es parejo\(\sqrt[n]{a^{n}}=|a|\).
\(4|n|\)
b.
\(-\sqrt{81 c^{2}}\)
Ya que\((9 c)^{2}=81 c^{2}\).
\(-\sqrt{(9 c)^{2}}\)
Ya que el índice\(n\) es parejo\(\sqrt[n]{a^{n}}=|a|\).
\(-9|c|\)
Simplificar:
- \(\sqrt{64 x^{2}}\)
- \(-\sqrt{100 p^{2}}\)
- Responder
-
- \(8|x|\)
- \(-10|p|\)
Simplificar:
- \(\sqrt{169 y^{2}}\)
- \(-\sqrt{121 y^{2}}\)
- Responder
-
- \(13|y|\)
- \(-11|y|\)
Este ejemplo solo lleva la idea más lejos ya que tiene raíces de índice más alto.
Simplificar:
- \(\sqrt[3]{64 p^{6}}\)
- \(\sqrt[4]{16 q^{12}}\)
Solución:
a.
\(\sqrt[3]{64 p^{6}}\)
Reescribir\(64p^{6}\) como\(\left(4 p^{2}\right)^{3}\).
\(\sqrt[3]{\left(4 p^{2}\right)^{3}}\)
Toma la raíz cubicada.
\(4p^{2}\)
b.
\(\sqrt[4]{16 q^{12}}\)
Reescribir el radicando como un cuarto poder.
\(\sqrt[4]{\left(2 q^{3}\right)^{4}}\)
Toma la cuarta raíz.
\(2|q^{3}|\)
Simplificar:
- \(\sqrt[3]{27 x^{27}}\)
- \(\sqrt[4]{81 q^{28}}\)
- Responder
-
- \(3x^{9}\)
- \(3|q^{7}|\)
Simplificar:
- \(\sqrt[3]{125 q^{9}}\)
- \(\sqrt[5]{243 q^{25}}\)
- Responder
-
- \(5p^{3}\)
- \(3q^{5}\)
Los siguientes ejemplos tienen dos variables.
Simplificar:
- \(\sqrt{36 x^{2} y^{2}}\)
- \(\sqrt{121 a^{6} b^{8}}\)
- \(\sqrt[3]{64 p^{63} q^{9}}\)
Solución:
a.
\(\sqrt{36 x^{2} y^{2}}\)
Desde\((6 x y)^{2}=36 x^{2} y^{2}\)
\(\sqrt{(6 x y)^{2}}\)
Toma la raíz cuadrada.
\(6|xy|\)
b.
\(\sqrt{121 a^{6} b^{8}}\)
Desde\(\left(11 a^{3} b^{4}\right)^{2}=121 a^{6} b^{8}\)
\(\sqrt{\left(11 a^{3} b^{4}\right)^{2}}\)
Toma la raíz cuadrada.
\(11\left|a^{3}\right| b^{4}\)
c.
\(\sqrt[3]{64 p^{63} q^{9}}\)
Desde\(\left(4 p^{21} q^{3}\right)^{3}=64 p^{63} q^{9}\)
\(\sqrt[3]{\left(4 p^{21} q^{3}\right)^{3}}\)
Toma la raíz cubicada.
\(4p^{21}q^{3}\)
Simplificar:
- \(\sqrt{100 a^{2} b^{2}}\)
- \(\sqrt{144 p^{12} q^{20}}\)
- \(\sqrt[3]{8 x^{30} y^{12}}\)
- Responder
-
- \(10|ab|\)
- \(12p^{6}q^{10}\)
- \(2x^{10}y^{4}\)
Simplificar:
- \(\sqrt{225 m^{2} n^{2}}\)
- \(\sqrt{169 x^{10} y^{14}}\)
- \(\sqrt[3]{27 w^{36} z^{15}}\)
- Responder
-
- \(15|mn|\)
- \(13\left|x^{5} y^{7}\right|\)
- \(3w^{12}z^{5}\)
Acceda a este recurso en línea para obtener instrucción y práctica adicionales con expresiones simplificadas con raíces.
- Simplificación de Exponentes de Variables con Raíces usando Valores Absolutos
Conceptos clave
- Notación de raíz cuadrada
- \(\sqrt{m}\)se lee 'la raíz cuadrada de\(m\) '
- Si\(n^{2}=m\), entonces\(n=\sqrt{m}\), para\(n≥0\).
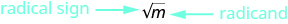
Figura 8.1.1 - La raíz cuadrada de\(m\),\(\sqrt{m}\), es un número positivo cuyo cuadrado es\(m\).
- n th Raíz de un número
- Si\(b^{n}=a\), entonces\(b\) es una\(n^{th}\) raíz de\(a\).
- La\(n^{th}\) raíz principal de\(a\) está escrita\(\sqrt[n]{a}\).
- \(n\)se llama el índice del radical.
- Propiedades de\(\sqrt[n]{a}\)
- Cuando\(n\) es un número par y
- \(a≥0\), entonces\(\sqrt[n]{a}\) es un número real
- \(a<0\), entonces no\(\sqrt[n]{a}\) es un número real
- Cuando\(n\) es un número impar,\(\sqrt[n]{a}\) es un número real para todos los valores de\(a\).
- Cuando\(n\) es un número par y
- Simplificación de raíces pares e impares
- Para cualquier entero\(n≥2\),
- cuando\(n\) es impar\(\sqrt[n]{a^{n}}=a\)
- cuando\(n\) es par\(\sqrt[n]{a^{n}}=|a|\)
- Debemos usar los signos de valor absoluto cuando tomamos una raíz par de una expresión con una variable en el radical.
- Para cualquier entero\(n≥2\),
Glosario
- cuadrado de un número
- Si\(n^{2}=m\), entonces\(m\) es el cuadrado de\(n\).
- raíz cuadrada de un número
- Si\(n^{2}=m\), entonces\(n\) es una raíz cuadrada de\(m\).


