2.9: Suplemento de ejercicio
- Page ID
- 112375
Suplemento de ejercicio
Símbolos y Notaciones
Para los siguientes problemas, simplifique las expresiones.
\(12 + 7(4 + 3)\)
- Responder
-
\(61\)
\(9(4 - 2) + 6(8 + 2) - 3(1 + 4)\)
\(6[1 + 8(7 + 2)]\)
- Responder
-
\(438\)
\(26 \div 2 - 10\)
\(\dfrac{(4+17+1)+4}{14-1}\)
- Responder
-
\(2\)
\(51 \div 3 \div 7\)
\((4 + 5)(4 + 6) - (4 + 7)\)
- Responder
-
\(79\)
\(8(2 \cdot 12 \div 13) + 2 \cdot 5 \cdot 11 - [1 + 4(1 + 2)]\)
\(\dfrac{3}{4} + \dfrac{1}{12}(\dfrac{3}{4} - \dfrac{1}{2})\)
- Responder
-
\(\dfrac{37}{47}\)
\(48 - 3[\dfrac{1 + 17}{6}]\)
\(\dfrac{29 + 11}{6 - 1}\)
- Responder
-
\(8\)
\(\dfrac{\dfrac{88}{11} + \dfrac{99}{9} + 1}{\dfrac{54}{9} - \dfrac{22}{11}}\)
\(\dfrac{8 \cdot 6}{2} + \dfrac{9 \cdot 9}{3} \dfrac{10 \cdot 4}{5}\)
- Responder
-
\(43\)
Para los siguientes problemas, escriba el símbolo de relación apropiado (=, <, >) en lugar de la ∗.
\(22 * 6\)
\(9[4 + 3(8)] * 6[1 + 8(5)]\)
- Responder
-
\(252 > 246\)
\(3(1.06 + 2.11) * 4(11.01 - 9.06)\)
\(2 * 0\)
- Responder
-
\(2 > 0\)
Para los siguientes problemas, indicar si las letras o símbolos son iguales o diferentes.
\(<\)y\(\not \ge\)
\(>\)y\(\not <\)
- Responder
-
Diferente
\(a = b\)y\(b = a\)
Representar la suma de\(c\) y\(d\) dos formas diferentes.
- Responder
-
\(c + d\);\(d + c\)
Para los siguientes problemas, use anotación algebraica.
\(8\)más\(9\)
\(62\)dividido por\(f\)
- Responder
-
\(\dfrac{62}{f}\)o\(62 \div f\)
\(8\)tiempos\((x + 4)\)
\(6\)veces\(x\), menos\(2\)
- Responder
-
\(6x - 2\)
\(x + 1\)dividido por\(x - 3\)
\(y + 11\)dividido por\(y + 10\), menos\(12\)
- Responder
-
\((y + 11) \div (y + 10) - 12\)o\(\dfrac{y + 11}{y + 10} - 12\)
cero menos\(a\) veces\(b\)
La línea numérica real y los números reales
¿Cada número natural es un número entero?
- Responder
-
Sí
¿Cada número racional es un número real?
Para los siguientes problemas, ubique los números en una recta numérica colocando un punto en su posición (aproximada).
\(2\)
- Responder
-
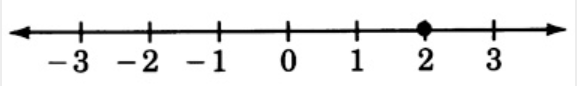
\(3.6\)
\(-1\dfrac{3}{8}\)
- Responder
-
\(0\)
\(-4\dfrac{1}{2}\)
- Responder
-
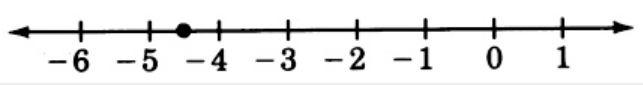
Dibuja una recta numérica que se extienda de 10 a 20. Coloque un punto en todos los enteros impares.
Dibuja una recta numérica que se extienda de\(−10\) a\(10\). Coloque un punto en todos los enteros impares negativos y en todos los enteros positivos pares.
- Responder
-
Dibuja una recta numérica que se extienda de\(−5\) a\(10\). Coloque un punto en todos los enteros que sean mayores entonces o iguales\(−2\) pero estrictamente menores que\(5\).
Dibuja una recta numérica que se extienda de\(−10\) a\(10\). Colocar un punto en todos los números reales que sean estrictamente mayores que\(−8\) pero menores o iguales a\(7\).
- Responder
-
Dibuja una recta numérica que se extienda de\(−10\) a\(10\). Coloque un punto en todos los números reales entre e incluyendo\(−6\) y\(4\).
Para los siguientes problemas, escriba el símbolo de relación apropiado (=, <, >).
\(-3\)\(0\)
- Responder
-
\(-3 < 0\)
\(-1\)\(1\)
\(-8\)\(-5\)
- Responder
-
\(-8 < -5\)
\(-5\)\(-5\dfrac{1}{2}\)
¿Hay un número entero de dos dígitos más pequeño? Si es así, ¿qué es?
- Responder
-
Sí,\(-99\)
¿Hay un número real de dos dígitos más pequeño? Si es así, ¿qué es?
Para los siguientes problemas, ¿qué enteros pueden sustituir a x para que las declaraciones sean verdaderas?
\(4 \le x \le 7\)
- Responder
-
\(4, 5, 6\)o\(7\)
\(-3 \le x < 1\)
\(-3\)\(0\)
- Responder
-
\(-3 < 0\)
\(-3 < x \le 2\)
- Responder
-
\(-2, -1, 0, 1\), o\(2\)
La temperatura hoy en Los Ángeles era de ochenta y dos grados. Representar esta temperatura por número real.
La temperatura hoy en Marbelhead era de seis grados bajo cero. Representar esta temperatura por número real.
- Responder
-
\(-6°\)
En la recta numérica, ¿cuántas unidades entre\(-3\) y\(2\)?
- Responder
-
\(-3 < 0\)
En la recta numérica, ¿cuántas unidades entre\(-4\) y\(0\)?
- Responder
-
\(4\)
Propiedades de los números reales
\(a + b = b + a\)es una ilustración de la propiedad de adición.
\(st = ts\)es una ilustración de la _________ propiedad de __________.
- Responder
-
conmutativo, multiplicación
Utilice las propiedades conmutativas de suma y multiplicación para escribir expresiones equivalentes para los siguientes problemas.
\(y + 12\)
\(a + 4b\)
- Responder
-
\(4b + a\)
\(6x\)
\(2(a-1)\)
- Responder
-
\((a-1)2\)
\((-8)(4)\)
\((6)(-9)(-2)\)
- Responder
-
\((-9)(6)(-2)\)o\((-9)(-2)(6)\) o\((6)(-2)(-9)\) o\((-2)(-9)(6)\)
\((x + y)(x - y)\)
\(△ \cdot ⋄\)
- Responder
-
\( ⋄\cdot △\)
Simplifique los siguientes problemas utilizando la propiedad conmutativa de la multiplicación. No es necesario utilizar la propiedad distributiva.
\(8x3y\)
\(16ab2c\)
- Responder
-
\(32abc\)
\(4axyc4d4e\)
\(3(x+2)5(x−1)0(x+6)\)
- Responder
-
\(0\)
\(8b(a−6)9a(a−4)\)
Para los siguientes problemas, utilice la propiedad distributiva para expandir las expresiones.
\(3(a + 4)\)
- Responder
-
\(3a + 12\)
\(a(b + 3c)\)
\(2g(4h + 2k\)
- Responder
-
\(8gh+4gk\)
\((8m+5n)6p\)
\(3y(2x+4z+5w)\)
- Responder
-
\(6xy+12yz+15wy\)
\((a+2)(b+2c)\)
\((x+y)(4a+3b)\)
- Responder
-
\(4ax+3bx+4ay+3by\)
\(10a_z(b_z + c)\)
Exponentes
Para los siguientes problemas, escriba las expresiones usando notación exponencial.
\(x\)a la quinta.
- Responder
-
\(x^5\)
\(y + 2\)en cubos.
\((a+2b)\)al cuadrado menos\((a+3b)\) al cuarto.
- Responder
-
\((a + 2b)^2 - (a + 3b)^4\)
\(x\)cubos más\(2\) veces\((y−x)\) hasta el séptimo.
\(aaaaaaa\)
- Responder
-
\(a^7\)
\(2 \cdot 2 \cdot 2 \cdot 2\)
\((−8)(−8)(−8)(−8)xxxyyyyy\)
- Responder
-
\((-8)^4x^3y^5\)
\((x-9)(x-9) + (3x + 1)(3x + 1)(3x + 1)\)
\(2zzyzyyy + 7zzyz(a - 6)^2(a-6)\)
- Responder
-
\(2y^4z^3 + 7yz^3(a-6)^3\)
Para los siguientes problemas, ampliar los términos para que no aparezcan exponentes.
\(x^3\)
\(3x^3\)
- Responder
-
\(3xxx\)
\(7^3x^2\)
\((4b)^2\)
- Responder
-
\(4b \cdot 4b\)
\((6a^2)^3(5c-4)^2\)
\((x^3+7)^2(y^2-3)^3(z+10)\)
- Responder
-
\((xxx+7)(xxx+7)(yy−3)(yy−3)(yy−3)(z+10)\)
Elija valores para\(a\) y\(b\) para mostrar que:
a. no siempre\(a+b)^2\) es igual a\(a^2 + b^2\)
b.\((a+b)^2\) Puede ser igual a\(a^2 + b^2\)
Elija el valor\(x\) para mostrar eso
a. no siempre\((4x)^2\) es igual a\(4x^2\).
b.\((4x)^2\) Puede ser igual a\(4x^2\)
- Responder
-
(a) cualquier valor excepto cero
(b) solo cero
Reglas de exponentes - Las reglas de poder para exponentes
Simplifica los siguientes problemas.
\(4^2 + 8\)
\(6^3 + 5(30)\)
- Responder
-
\(366\)
\(1^8 + 0^{10} + 3^2(4^2 + 2^3)\)
\(12^2 + 0.3(11)^2\)
- Responder
-
\(180.3\)
\(\dfrac{3^4 + 1}{2^2 + 4^2 + 3^2}\)
\(\dfrac{6^2 + 3^2}{2^2 + 1} + \dfrac{(1+4)^2 - 2^3 - 1^4}{2^5-4^2}\)
- Responder
-
\(10\)
\(a^4a^3\)
\(2b^52b^3\)
- Responder
-
\(4b^8\)
\(4a^3b^2c^8 \cdot 3ab^2c^0\)
\((6x^4y^{10})(xy^3)\)
- Responder
-
\(6x^5y^{13}\)
\((3xyz^2)(2x^2y^3)(4x^2y^2z^4)\)
\((3a)^4\)
- Responder
-
\(81a^4\)
\((10xy)^2\)
\((x^2y^4)^6\)
- Responder
-
\(x^{12}y^{24}\)
\((a^4b^7c^7z^{12})^9\)
\((\dfrac{3}{4}x^8y^6z^0a^{10}b^{15})^2\)
- Responder
-
\(\dfrac{9}{16}x^{16}y^{12}a^{20}b^{30}\)
\(\dfrac{14a^4b^6c^7}{2ab^3c^2}\)
- Responder
-
\(7a^3b^3c^5\)
\(\dfrac{11x^4}{11x^4}\)
\(x^4 \cdot \dfrac{x^{10}}{x^3}\)
- Responder
-
\(x^{11}\)
\(a^3b^7 \cdot \dfrac{a^9b^6}{a^5b^{10}}\)
\(\dfrac{(x^4y^6z^{10})^4}{(xy^5z^7)^3}\)
- Responder
-
\(x^{13}y^9z^{19}\)
\(\dfrac{(2x-1)^{13}(2x+5)^5}{(2x-1)^{10}(2x+5)}\)
\((\dfrac{3x^2}{4y^3})^2\)
- Responder
-
\(\dfrac{9x^4}{16y^6}\)
\(\dfrac{(x+y)^9(x-y)^4}{(x+y)^3}\)
\(x^n \cdot x^m\)
- Responder
-
\(x^{n+m}\)
\(a^{n+2}a^{n+4}\)
\(6b^{2n+7} \cdot 8b^{5n+2}\)
- Responder
-
\(48b^{7n+9}\)
\(\dfrac{18x^{4n+9}}{2x^{2n+1}}\)
\((x^{5t}y^{4r})^7\)
- Responder
-
\(x^{35t}y^{28r}\)
\((a^{2n}b^{3m}c^{4p})^{6r}\)
\(\dfrac{u^w}{u^k}\)
- Responder
-
\(u^{w-k}\)