9.6: Suma y resta de expresiones de raíz cuadrada
- Page ID
- 112378
La lógica detrás del proceso
Ahora estudiaremos métodos de simplificación de expresiones radicales como
\(4\sqrt{3} + 8\sqrt{3}\)o\(5\sqrt{2x} - 11\sqrt{2x} + 4(\sqrt{2x} + 1)\)
El procedimiento para sumar y restar expresiones de raíz cuadrada se hará evidente si pensamos en el procedimiento que utilizamos para simplificar expresiones polinómicas como
\(4x + 8x\) o\(5a - 11a + 4(a+1)\)
Las variables\(x\) y\(a\) son letras que representan algunas cantidades desconocidas (quizás\(x\) representa\(\sqrt{3}\) y\(a\) representa\(\sqrt{2x}\)). Combinar términos similares nos da
\ (\ begin {array} {vaciado izquierdo}
4x + 8x = 12x &\ text {o} & 4\ sqrt {3} + 8\ sqrt {3} = 12\ sqrt {3}\\ text {y}
\\
5a - 11a + 4 (a + 1) &\ text {o} & 5\ sqrt {2x} - 11\ sqrt {2x} + 4 (\ sqrt {2x} + 4 (\ sqrt rt {2x} + 1)\\
5a - 11a + 4a + 4 && 5\ sqrt {2x} - 11\ sqrt {2x} + 4\ sqrt {2x} + 4\\
-2a && -2\ sqrt {2x} + 4
\ end {array}\)
El Proceso
Consideremos la expresión\(4\sqrt{3} + 8\sqrt{3}\). Hay dos formas de ver el proceso de simplificación.
Estamos preguntando: “¿Cuántas raíces cuadradas de\(3\) tenemos?”
\(4 \sqrt{3}\)significa que tenemos\(4\) “raíces cuadradas de\(3\)”
Así, en conjunto tenemos\(12\) “raíces cuadradas de”\(3\).
También podemos usar la idea de combinar términos similares. Si recordamos, el proceso de combinación de términos similares se basa en la propiedad distributiva
\(4x + 8x = 12x\)porque\(4x + 8x = (4 + 8)x = 12x\)
Podríamos simplificar el\(4\sqrt{3} + 8\sqrt{3}\) uso de la propiedad distributiva.
4\ sqrt {3} + 8\ sqrt {3} = (4 + 8)\ sqrt {3} = 12\ sqrt {3}\)
Ambos métodos nos darán el mismo resultado. El primer método es probablemente un poco más rápido, pero ten en cuenta, sin embargo, que el proceso funciona porque se basa en una de las reglas básicas del álgebra, la propiedad distributiva de los números reales.
Conjunto de Muestras A
Simplifica las siguientes expresiones radicales.
\(-6\sqrt{10} + 11\sqrt{10} = 5\sqrt{10}\)
\(4\sqrt{32} + 5\sqrt{2} \text{ Simplify } \sqrt{32}\)
\ (\ begin {array} {ras izquierda}
4\ sqrt {16\ cdot 2} + 5\ sqrt {2} &= 4\ sqrt {16}\ sqrt {2} + 5\ sqrt {2}\\
&= 4\ cdot 4\ sqrt {2} + 5\ sqrt {2}\\
&= 16\ sqrt {2} + 5\ sqrt {2}}\\
&=21\ sqrt {2}
\ end {array}\)
\(-3x\sqrt{75} + 2x\sqrt{48} - x\sqrt{27} \text{ Simplify each of the three radicals}\)
\ (\ begin {array} {ras a la izquierda}
-3x\ sqrt {75} + 2x\ sqrt {48} - x\ sqrt {27} &= -3x\ sqrt {25\ cdot 3} + 2x\ sqrt {16\ cdot 3} - x\ sqrt {9\ cdot 2}\\
&= -15x\ sqrt {3} + 8x\ sqrt {3} - 3x\ sqrt {3}\\
& =( -15x + 8x - 3x)\ sqrt {3}\\
&=-10x\ sqrt {3}
\ end {array}\)
\(5a\sqrt{24a^3} - 7\sqrt{54a^5} + a^2\sqrt{6a} + 6a \text{ Simplify each radical}\)
\ (\ begin {array} {vaciado a la izquierda}
5a\ sqrt {24a^3} - 7\ sqrt {54a^5} + a^2\ sqrt {6a} + 6a &= 5a\ sqrt {4\ cdot 6\ cdot a^2\ cdot a} - 7\ sqrt {9\ cdot 6\ cdot a^4\ cdot a} + a^2\ sqrt {6a} + 6a\\
&= 10a^2\ sqrt {6a} - 21a^2\ sqrt {6a} + a^2\ sqrt {6a} + 6a\\
&= (10a^2 - 21a^2 + a^ 2)\ sqrt {6a} + 6a\\
&= -10a^2\ sqrt {6a} + 6a\
&= -2a (5a\ sqrt {6a} - 3)
\ end {array}\)
Conjunto de práctica A
Encuentra cada suma o diferencia.
\(4\sqrt{18} - 5\sqrt{8}\)
- Responder
-
\(2\sqrt{2}\)
\(6x\sqrt{48} + 8x\sqrt{75}\)
- Responder
-
\(64x\sqrt{3}\)
\(-7\sqrt{84x} - 12\sqrt{189x} + 2\sqrt{21x}\)
- Responder
-
\(-48\sqrt{21x}\)
\(9\sqrt{6} - 8\sqrt{6} + 3\)
- Responder
-
\(\sqrt{6} + 3\)
\(\sqrt{a^3} + 4a\sqrt{a}\)
- Responder
-
\(5a\sqrt{a}\)
\(4x\sqrt{54x^3} + \sqrt{36x^2} + 3\sqrt{24x^5} - 3x\)
- Responder
-
\(18x^2\sqrt{6x} + 3x\)
Conjunto de Muestras B

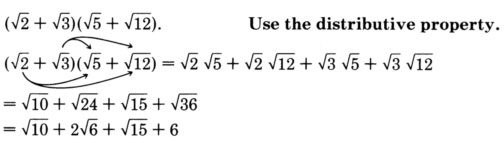
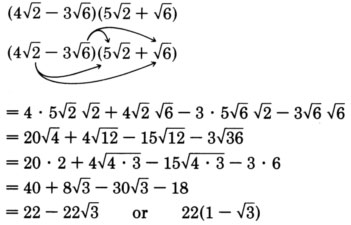
\(\dfrac{3 + \sqrt{8}}{3 - \sqrt{8}}\)Racionalizaremos el denominador multiplicando esta fracción por\(1\) en la forma\(\dfrac{3 + \sqrt{8}}{3 + \sqrt{8}}\).
\ (\ begin {array} {ras izquierda}
\ dfrac {3+\ sqrt {8}} {3-\ sqrt {8}}\ cdot\ frac {3+\ sqrt {8}} {3+\ sqrt {8}} &=\ dfrac {(3+\ sqrt {8}) (3+\ sqrt {8})} {3^ {2} - (\ sqrt {8})} {3^ {2} - (\ sqrt {8}) ^ {2}}\\
&=\ dfrac {9+3\ sqrt {8} +3\ sqrt {8} +\ sqrt {8}\ sqrt {8}} {9-8}\\
&=\ dfrac {9+6\ sqrt {8} +8} {1}\\
&=17+6\ sqrt {8}\\
&=17+6\ sqrt {4\ cdot 2}\\
&=17+12\ sqrt {2}
\ end {array}\)
\(\dfrac{2 + \sqrt{7}}{4 - \sqrt{3}}\). Racionalizar el denominador multiplicando esta fracción por\(1\) en la forma\(\dfrac{4 + \sqrt{3}}{4 + \sqrt{3}}\).
\ (\ begin {array} {vaciado izquierdo}
\ dfrac {2+\ sqrt {7}} {4-\ sqrt {3}}\ cdot\ dfrac {4+\ sqrt {3}} {4+\ sqrt {3}} &=\ dfrac {(2+\ sqrt {7}) (4+\ sqrt {3})} {4^ {2} - (\ sqrt {3}) ^ {2}}\\
&=\ dfrac {8+2\ sqrt {3} +4\ sqrt {7} +\ sqrt {21}} {16-3}\
&=\ dfrac {8+2\ sqrt {3} +4\ sqrt {7} +\ sqrt {21}} {13}
\ end {array}\)
Set de práctica B
Simplifique cada uno realizando la operación indicada.
\(\sqrt{5}(\sqrt{6} - 4)\)
- Responder
-
\(\sqrt{30} - 4\sqrt{5}\)
\((\sqrt{5} + \sqrt{7})(\sqrt{2} + \sqrt{8})\)
- Responder
-
\(3\sqrt{10} + 3\sqrt{14}\)
\((3\sqrt{2} - 2\sqrt{3})(4\sqrt{3} + \sqrt{8})\)
- Responder
-
\(8\sqrt{6} - 12\)
\(\dfrac{4 + \sqrt{5}}{3 - \sqrt{8}}\)
- Responder
-
\(12 + 8\sqrt{2} + 3\sqrt{5} + 2\sqrt{10}\)
Ejercicios
Para los siguientes problemas, simplifique cada expresión realizando la operación indicada.
\(4\sqrt{5} - 2\sqrt{5}\)
- Responder
-
\(2\sqrt{5}\)
\(10 \sqrt{2} + 8\sqrt{2}\)
\(-3\sqrt{6} - 12\sqrt{6}\)
- Responder
-
\(-15 \sqrt{6}\)
\(-\sqrt{10} - 2\sqrt{10}\)
\(3\sqrt{7x} + 2\sqrt{7x}\)
- Responder
-
\(5\sqrt{7x}\)
\(6\sqrt{3a} + \sqrt{3a}\)
\(2\sqrt{18} + 5\sqrt{32}\)
- Responder
-
\(26\sqrt{2}\)
\(4\sqrt{27} - 3\sqrt{48}\)
\(\sqrt{200} - \sqrt{128}\)
- Responder
-
\(2\sqrt{2}\)
\(4\sqrt{300} + 2\sqrt{500}\)
\(6\sqrt{40} + 8\sqrt{80}\)
- Responder
-
\(12\sqrt{10} + 32\sqrt{5}\)
\(2\sqrt{120} - 5\sqrt{30}\)
\(8\sqrt{60} - 3\sqrt{15}\)
- Responder
-
\(13\sqrt{15}\)
\(\sqrt{a^3} - 3a\sqrt{a}\)
\(\sqrt{4x^3} + x\sqrt{x}\)
- Responder
-
\(3x\sqrt{x}\)
\(2b\sqrt{a^3b^5} + 6a\sqrt{ab^7}\)
\(5xy\sqrt{2xy^3} - 3y^2\sqrt{2x^3y}\)
- Responder
-
\(2xy^2\sqrt{2xy}\)
\(5\sqrt{20} + 3\sqrt{45} - 3\sqrt{40}\)
\(\sqrt{24} - 2\sqrt{54} - 4\sqrt{12}\)
- Responder
-
\(-4\sqrt{6} - 8\sqrt{3}\)
\(6\sqrt{18} + 5\sqrt{32} + 4\sqrt{50}\)
\(-8\sqrt{20} - 9\sqrt{125} + 10\sqrt{180}\)
- Responder
-
\(-\sqrt{5}\)
\(2\sqrt{27} + 4\sqrt{3} - 6\sqrt{12}\)
\(\sqrt{14} + 2\sqrt{56} - 3\sqrt{136}\)
- Responder
-
\(5\sqrt{14} - 6\sqrt{34}\)
\(3\sqrt{2} + 2\sqrt{63} + 5\sqrt{7}\)
\(4ax\sqrt{3x} + 2\sqrt{3a^2x^3} + 7\sqrt{3a^2x^3}\)
- Responder
-
\(13ax\sqrt{3x}\)
\(3by\sqrt{5y} + 4\sqrt{5b^2y^3} - 2\sqrt{5b^2y^3}\)
\(\sqrt{2}(\sqrt{3} + 1)\)
- Responder
-
\(\sqrt{6} + \sqrt{2}\)
\(\sqrt{3}(\sqrt{5} - 3)\)
\(\sqrt{5}(\sqrt{3} - \sqrt{2})\)
- Responder
-
\(\sqrt{15} - \sqrt{10}\)
\(\sqrt{7}(\sqrt{6} - \sqrt{3})\)
\(\sqrt{8}(\sqrt{3} + \sqrt{2})\)
- Responder
-
\(2(\sqrt{6} + 2)\)
\(\sqrt{10}(\sqrt{10} - \sqrt{5})\)
\((1 + \sqrt{3})(2 - \sqrt{3})\)
- Responder
-
\(-1 + \sqrt{3}\)
\((5 + \sqrt{6})(4 - \sqrt{6})\)
\((3 - \sqrt{2})(4 - \sqrt{2})\)
- Responder
-
\(7(2 - \sqrt{2})\)
\((5 + \sqrt{7})(4 - \sqrt{7})\)
\((\sqrt{2} + \sqrt{5})(\sqrt{2} + 3\sqrt{5})\)
- Responder
-
\(17 + 4\sqrt{10}\)
\((2\sqrt{6} - \sqrt{3})(3\sqrt{6} + 2\sqrt{3})\)
\((4\sqrt{5} - 2\sqrt{3})(3\sqrt{5} + \sqrt{3})\)
- Responder
-
\(54 - 2\sqrt{15}\)
\((3\sqrt{8} - 2\sqrt{2})(4\sqrt{2} - 5\sqrt{8})\)
\((\sqrt{12} + 5\sqrt{3})(2\sqrt{3} - 2\sqrt{12})\)
- Responder
-
\(-42\)
\((1 + \sqrt{3})^2\)
\((3 + \sqrt{5})^2\)
- Responder
-
\(14 + 6\sqrt{5}\)
\((2 - \sqrt{6})^2\)
\((2 - \sqrt{7})^2\)
- Responder
-
\(11 - 4\sqrt{7}\)
\((1 + \sqrt{3x})^2\)
\((2 + \sqrt{5x})^2\)
- Responder
-
\(4 + 4\sqrt{5x} + 5x\)
\((3 - \sqrt{3x})^2\)
\((8 - \sqrt{6b})^2\)
- Responder
-
\(64 - 16\sqrt{6b} + 6b\)
\((2a + \sqrt{5a})^2\)
\((3y - \sqrt{7y})^2\)
- Responder
-
\(9y^2 - 6y\sqrt{7y} + 7y\)
\((3 + \sqrt{3})(3 - \sqrt{3})\)
\((2 + \sqrt{5})(2 - \sqrt{5})\)
- Responder
-
\(-1\)
\((8 + \sqrt{10})(8 - \sqrt{10})\)
\((6 + \sqrt{7})(6 - \sqrt{7})\)
- Responder
-
\(29\)
\((\sqrt{2} + \sqrt{3})(\sqrt{2} - \sqrt{3}\)
\((\sqrt{5} + \sqrt{2})(\sqrt{5} - \sqrt{2})\)
- Responder
-
\(3\)
\((\sqrt{a} + \sqrt{b})(\sqrt{a} - \sqrt{b})\)
\((\sqrt{x} + \sqrt{y})(\sqrt{x} - \sqrt{y})\)
- Responder
-
\(x - y\)
\(\dfrac{2}{5 + \sqrt{3}}\)
\(\dfrac{4}{6 + \sqrt{2}}\)
- Responder
-
\(\dfrac{2(6 - \sqrt{2})}{17}\)
\(\dfrac{1}{3 - \sqrt{2}}\)
\(\dfrac{1}{4 - \sqrt{3}}\)
- Contestar
-
\(\dfrac{4 + \sqrt{3}}{13}\)
\(\dfrac{8}{2 - \sqrt{6}}\)
\(\dfrac{2}{3 - \sqrt{7}}\)
- Contestar
-
\(3 + \sqrt{7}\)
\(\dfrac{\sqrt{5}}{3 + \sqrt{3}}\)
\(\dfrac{\sqrt{3}}{6 + \sqrt{6}}\)
- Contestar
-
\(\dfrac{2\sqrt{3} - \sqrt{2}}{10}\)
\(\dfrac{2 - \sqrt{8}}{2 + \sqrt{8}}\)
\(\dfrac{4 + \sqrt{5}}{4 - \sqrt{5}}\)
- Contestar
-
\(\dfrac{21 + 8\sqrt{5}}{11}\)
\(\dfrac{1 + \sqrt{6}}{1 - \sqrt{6}}\)
\(\dfrac{8 - \sqrt{3}}{2 + \sqrt{18}}\)
- Contestar
-
\(\dfrac{-16 + 2\sqrt{3} + 24\sqrt{2} - 3\sqrt{6}}{14}\)
\(\dfrac{6 - \sqrt{2}}{4 + \sqrt{12}}\)
\(\dfrac{\sqrt{3} - \sqrt{2}}{\sqrt{3} + \sqrt{2}}\)
- Contestar
-
\(5 - 2\sqrt{6}\)
\(\dfrac{\sqrt{6a} - \sqrt{8a}}{\sqrt{8a} + \sqrt{6a}}\)
\(\dfrac{\sqrt{2b} - \sqrt{3b}}{\sqrt{3b} + \sqrt{2b}}\)
- Contestar
-
\(2\sqrt{6} - 5\)
Ejercicios para revisión
Simplificar\((\dfrac{x^5y^3}{x^2y})^5\)
Simplificar\((8x^3y)^2(x^2y^3)^4\)
- Contestar
-
\(64x^{14}y^{14}\)
Escribe\((x-1)^4(x-1)^{-7}\) para que solo aparezcan exponentes positivos.
Simpify\(\sqrt{27x^5y^{10}z^3}\)
- Contestar
-
\(3x^2y^5z\sqrt{3xz}\)
Simplificar\(\dfrac{1}{2 + \sqrt{x}}\) racionalizando el denominador.


