9.5: División de expresiones de raíz cuadrada
- Page ID
- 112379
La División Propiedad de Raíces Cuadradas
En nuestro trabajo con la simplificación de expresiones de raíz cuadrada, señalamos que
\[\sqrt{\dfrac{x}{y}} = \dfrac{\sqrt{x}}{\sqrt{y}} \nonumber\]
Como esta es una ecuación, podemos escribirla como:
\[\dfrac{\sqrt{x}}{\sqrt{y}} = \sqrt{\dfrac{x}{y}} \nonumber\]
Para dividir dos expresiones de raíz cuadrada, utilizamos la propiedad de división de raíces cuadradas:
\[\dfrac{\sqrt{x}}{\sqrt{y}} = \sqrt{\dfrac{x}{y}}\]
El cociente de la raíz cuadrada es la raíz cuadrada del cociente.
Racionalización del denominador
Como podemos ver al observar el lado derecho de la ecuación que rige la división de raíces cuadradas, el proceso puede producir una fracción en el radicando. Esto significa, por supuesto, que la expresión de raíz cuadrada no está en forma simplificada. A veces es más útil racionalizar el denominador de una expresión de raíz cuadrada antes de realizar realmente la división.
Conjunto de Muestras A
Simplifica las expresiones de raíz cuadrada.
\[\sqrt{\dfrac{3}{7}} \nonumber\]
Esta expresión radical no está en forma simplificada ya que hay una fracción bajo el signo radical. Podemos eliminar este problema usando la propiedad de división de raíces cuadradas.
\[\sqrt{\dfrac{3}{7}} = \dfrac{\sqrt{3}}{\sqrt{7}} = \dfrac{\sqrt{3}}{\sqrt{7}} \cdot \dfrac{\sqrt{7}}{\sqrt{7}} = \dfrac{\sqrt{3} \sqrt{7}}{7} = \dfrac{\sqrt{21}}{7} \nonumber\]
\(\dfrac{\sqrt{5}}{\sqrt{3}}\)
Una aplicación directa de la regla produce\(\sqrt{\dfrac{5}{3}}\), la cual debe simplificarse. Racionalicemos el denominador antes de realizar la división.
\(\dfrac{\sqrt{5}}{\sqrt{3}}=\dfrac{\sqrt{5}}{\sqrt{3}} \cdot \dfrac{\sqrt{3}}{\sqrt{3}}=\dfrac{\sqrt{5} \sqrt{3}}{3}=\dfrac{\sqrt{15}}{3}\)
\(\dfrac{\sqrt{21}}{\sqrt{7}} = \sqrt{\dfrac{21}{7}} = \sqrt{3}\)
La regla produce el cociente rápidamente. También podríamos racionalizar primero el denominador y producir el mismo resultado.
\(\dfrac{\sqrt{21}}{\sqrt{7}}=\dfrac{\sqrt{21}}{7} \cdot \dfrac{\sqrt{7}}{\sqrt{7}}=\dfrac{\sqrt{21 \cdot 7}}{7}=\dfrac{\sqrt{3 \cdot 7 \cdot 7}}{7}=\dfrac{\sqrt{3 \cdot 7^{2}}}{7}=\dfrac{7 \sqrt{3}}{7}=\sqrt{3}\)
\(\dfrac{\sqrt{80 x^{9}}}{\sqrt{5 x^{4}}}=\sqrt{\dfrac{80 x^{9}}{5 x^{4}}}=\sqrt{16 x^{5}}=\sqrt{16} \sqrt{x^{4} x}=4 x^{2} \sqrt{x}\)
\(\dfrac{\sqrt{50 a^{3} b^{7}}}{\sqrt{5 a b^{5}}}=\sqrt{\dfrac{50 a^{3} b^{7}}{5 a b^{5}}}=\sqrt{10 a^{2} b^{2}}=a b \sqrt{10}\)
\(\dfrac{\sqrt{5a}}{\sqrt{b}}\)
Alguna observación muestra que una división directa de los radicandos producirá una fracción. Esto sugiere que primero racionalizamos el denominador.
\(\dfrac{\sqrt{5a}}{\sqrt{b}} = \dfrac{\sqrt{5a}}{\sqrt{b}} \cdot \dfrac{\sqrt{b}}{\sqrt{b}} = \dfrac{\sqrt{5a} \sqrt{b}}{b} = \dfrac{\sqrt{5ab}}{b}\)
\(\dfrac{\sqrt{m-6}}{\sqrt{m+2}} = \dfrac{\sqrt{m-6}}{\sqrt{m+2}} \cdot \dfrac{\sqrt{m+2}}{\sqrt{m+2}} = \dfrac{\sqrt{m^2 - 4m - 12}}{m + 2}\)
\(\dfrac{\sqrt{y^{2}-y-12}}{\sqrt{y+3}}=\sqrt{\dfrac{y^{2}-y-12}{y+3}}=\sqrt{\dfrac{(y+3)(y-4)}{(y+3)}}=\sqrt{\dfrac{\cancel{(y+3)}(y-4)}{\cancel{(y+3)}}}=\sqrt{y-4}\)
Conjunto de práctica A
Simplifica las expresiones de raíz cuadrada.
\(\dfrac{\sqrt{26}}{\sqrt{13}}\)
- Contestar
-
\(\sqrt{2}\)
\(\dfrac{\sqrt{7}}{\sqrt{3}}\)
- Contestar
-
\(\dfrac{\sqrt{21}}{3}\)
\(\dfrac{\sqrt{80m^5n^8}}{\sqrt{5m^2n}}\)
- Contestar
-
\(4mn^3 \sqrt{mn}\)
\(\dfrac{\sqrt{196(x+7)^8}}{\sqrt{2(x+7)^3}}\)
- Contestar
-
\(7(x+7)^2 \sqrt{2(x+7)}\)
\(\dfrac{\sqrt{n+4}}{\sqrt{n-5}}\)
- Contestar
-
\(\dfrac{\sqrt{n^2 - n - 20}}{n-5}\)
\(\dfrac{\sqrt{a^2 - 6a + 8}}{\sqrt{a-2}}\)
- Contestar
-
\(\sqrt{a-4}\)
\(\dfrac{\sqrt{x^{2n}}}{\sqrt{x^n}}\)
- Contestar
-
\(x^n\)
\(\dfrac{\sqrt{a^{3m-5}}}{\sqrt{a^{m-1}}}\)
- Contestar
-
\(a^{m-2}\)
Conjugados y racionalización del denominador
Para realizar una división que contenga un binomio en el denominador, tal como\(\dfrac{3}{4 + \sqrt{6}}\), multiplicamos el numerador y el denominador por un conjugado del denominador.
Un conjugado del binomio\(a + b\) es\(a-b\). De igual manera, un conjugado de\(a-b\) es\(a + b\).
Observe que cuando los conjugados\(a + b\) y\(a - b\) se multiplican juntos, producen una diferencia de dos cuadrados.
\((a+b)(a-b) = a^2 - ab + ab - b^2 = a^2 - b^2\)
Este principio nos ayuda a eliminar los radicales de raíz cuadrada, como se muestra en estos ejemplos que ilustran el producto de los conjugados.
\ (\ begin {array} {ruedado}
(5 +\ sqrt {2}) (5 -\ sqrt {2}) &= 5^2 - (\ sqrt {2}) ^2\\
&= 25 - 2\\
&= 23
\ end {array}\)
\ (\ begin {array} {ras a la izquierda}
(\ sqrt {6} -\ sqrt {7}) (\ sqrt {6} +\ sqrt {7}) &= (\ sqrt {6}) ^2 - (\ sqrt {7}) ^2\\
&= 6 - 7\
&= -1
\ end {array}\)
Conjunto de Muestras B
Simplifica las siguientes expresiones.
\(\dfrac{3}{4 + \sqrt{6}}\)
El conjugado del denominador es\(4 - \sqrt{6}\). Multiplicar la fracción por\(1\) en forma de\(\dfrac{4 - \sqrt{6}}{4 - \sqrt{6}}\)
\ (\ begin {array} {ras a la izquierda}
\ dfrac {3} {4 +\ sqrt {6}}\ cdot\ dfrac {4 -\ sqrt {6}} {4 -\ sqrt {6}} &=\ dfrac {3 (4 -\ sqrt {6})} {4^2 - (\ sqrt {6}) ^2}\
&=\ dfrac {12 - 3\ sqrt {6}} {16 - 6}\\
&=\ dfrac {12 - 3\ sqrt {6}} {10}
\ end {array}\)
\(\dfrac{\sqrt{2x}}{\sqrt{3} - \sqrt{5x}}\)
El conjugado del denominador es\(\sqrt{3} + \sqrt{5x}\). Multiplique la fracción por\(1\) en forma de\(\dfrac{\sqrt{3} + \sqrt{5x}}{\sqrt{3} + \sqrt{5x}}\).
\ (\ begin {array} {ras izquierda}
\ dfrac {\ sqrt {2 x}} {\ sqrt {3} -\ sqrt {5 x}}\ cdot\ dfrac {\ sqrt {3} +\ sqrt {5 x}} {\ sqrt {3} +\ sqrt {5 x}} &=\ dfrac {\ sqrt {2 x} (\ sqrt {3} +\ sqrt {5 x})} {(\ sqrt {3}) ^ {2} - (\ sqrt {5 x}) ^ {2}}\\
&=\ dfrac {\ sqrt {2 x}\ sqrt {3} +\ sqrt {2 x}\ sqrt {5 x}} {3-5 x}\
&=\ dfrac {\ sqrt {6 x} +\ sqrt {10 x^ {2}}} {3-5 x}\\
&=\ dfrac {\ sqrt {6 x} +x\ sqrt {10}} {3-5 x}
\ end {array}\)
Set de práctica B
Simplifica las siguientes expresiones.
\(\dfrac{5}{9 + \sqrt{7}}\)
- Contestar
-
\(\dfrac{45 - 5\sqrt{7}}{74}\)
\(\dfrac{-2}{1 - \sqrt{3x}}\)
- Contestar
-
\(\dfrac{-2 - 2\sqrt{3x}}{1 - 3x}\)
\(\dfrac{\sqrt{8}}{\sqrt{3x} + \sqrt{2x}}\)
- Contestar
-
\(\dfrac{2\sqrt{6x} - 4\sqrt{x}}{x}\)
\(\dfrac{\sqrt{2m}}{m - \sqrt{3m}}\)
- Contestar
-
\(\dfrac{\sqrt{2m} + \sqrt{6}}{m - 3}\)
Ejercicios
Para los siguientes problemas, simplifique cada expresión.
\(\dfrac{\sqrt{28}}{\sqrt{2}}\)
- Contestar
-
\(\sqrt{14}\)
\(\dfrac{\sqrt{200}}{\sqrt{10}}\)
\(\dfrac{\sqrt{28}}{\sqrt{7}}\)
- Contestar
-
\(2\)
\(\dfrac{\sqrt{96}}{\sqrt{24}}\)
\(\dfrac{\sqrt{180}}{\sqrt{5}}\)
- Contestar
-
\(6\)
\(\dfrac{\sqrt{336}}{\sqrt{21}}\)
\(\dfrac{\sqrt{162}}{\sqrt{18}}\)
- Contestar
-
\(3\)
\(\sqrt{\dfrac{25}{9}}\)
\(\sqrt{\dfrac{36}{35}}\)
- Contestar
-
\(\dfrac{6\sqrt{35}}{35}\)
\(\sqrt{\dfrac{225}{16}}\)
\(\sqrt{\dfrac{49}{225}}\)
- Contestar
-
\(\dfrac{7}{15}\)
\(\sqrt{\dfrac{3}{5}}\)
\(\sqrt{\dfrac{3}{7}}\)
- Contestar
-
\(\dfrac{\sqrt{21}}{7}\)
\(\sqrt{\dfrac{1}{2}}\)
\(\sqrt{\dfrac{5}{2}}\)
- Contestar
-
\(\dfrac{\sqrt{10}}{2}\)
\(\sqrt{\dfrac{11}{25}}\)
\(\sqrt{\dfrac{15}{36}}\)
- Contestar
-
\(\dfrac{\sqrt{15}}{6}\)
\(\sqrt{\dfrac{5}{16}}\)
\(\sqrt{\dfrac{7}{25}}\)
- Contestar
-
\(\dfrac{\sqrt{7}}{5}\)
\(\sqrt{\dfrac{32}{49}}\)
\(\sqrt{\dfrac{50}{81}}\)
- Contestar
-
\(\dfrac{5 \sqrt{2}}{9}\)
\(\dfrac{\sqrt{125x^5}}{\sqrt{5x^3}}\)
\(\dfrac{\sqrt{72m^7}}{\sqrt{2m^3}}\)
- Contestar
-
\(6m^2\)
\(\dfrac{\sqrt{162a^{11}}}{\sqrt{2a^5}}\)
\(\dfrac{\sqrt{75y^{10}}}{\sqrt{2a^5}}\)
- Contestar
-
\(5y^3\)
\(\dfrac{\sqrt{48x^9}}{\sqrt{3x^2}}\)
\(\dfrac{\sqrt{125a^{14}}}{\sqrt{5a^5}}\)
- Contestar
-
\(5a^4 \sqrt{a}\)
\(\dfrac{\sqrt{27a^{10}}}{\sqrt{3a^5}}\)
\(\dfrac{\sqrt{108x^{21}}}{\sqrt{3x^4}}\)
- Contestar
-
\(6x^8 \sqrt{x}\)
\(\dfrac{\sqrt{48x^6y^7}}{\sqrt{3xy}}\)
\(\dfrac{\sqrt{45a^3b^8c^2}}{\sqrt{5ab^2c}}\)
- Contestar
-
\(3ab^3 \sqrt{c}\)
\(\dfrac{\sqrt{66m^{12}n^{15}}}{\sqrt{11mn^8}}\)
\(\dfrac{\sqrt{30p^5q^{14}}}{\sqrt{5q^7}}\)
- Contestar
-
\(p^2q^3 \sqrt{6pq}\)
\(\dfrac{\sqrt{b}}{\sqrt{5}}\)
\(\dfrac{\sqrt{5x}}{\sqrt{2}}\)
- Contestar
-
\(\dfrac{\sqrt{10x}}{2}\)
\(\dfrac{\sqrt{2a^3b}}{\sqrt{14a}}\)
\(\dfrac{\sqrt{3m^4n^3}}{\sqrt{6mn^5}}\)
- Contestar
-
\(\dfrac{m \sqrt{2m}}{2n}\)
\(\dfrac{\sqrt{5(p-q)^6(r+s)^4}}{\sqrt{25(r+s)^3}}\)
\(\dfrac{\sqrt{m(m-6)-m^2 + 6m}}{\sqrt{3m - 7}}\)
- Contestar
-
\(0\)
\(\dfrac{\sqrt{r+1}}{\sqrt{r-1}}\)
\(\dfrac{\sqrt{s+3}}{\sqrt{s-3}}\)
- Contestar
-
\(\dfrac{\sqrt{s^2-9}}{s-3}\)
\(\dfrac{\sqrt{a^2 + 3a + 2}}{\sqrt{a + 1}}\)
\(\dfrac{\sqrt{x^2 - 10x + 24}}{\sqrt{x-4}}\)
- Contestar
-
\(\sqrt{x-6}\)
\(\dfrac{\sqrt{x^2 - 2x - 8}}{\sqrt{x + 2}}\)
\(\dfrac{\sqrt{x^2 - 4x + 3}}{\sqrt{x-3}}\)
- Contestar
-
\(\sqrt{x-1}\)
\(\dfrac{\sqrt{2x^2 - x - 1}}{\sqrt{x - 1}}\)
\(\dfrac{-5}{4 + \sqrt{5}}\)
- Contestar
-
\(\dfrac{-20 + 5\sqrt{5}}{11}\)
\(\dfrac{1}{1 + \sqrt{x}}\)
\(\dfrac{2}{1 - \sqrt{a}}\)
- Contestar
-
\(\dfrac{2(1 + \sqrt{a})}{1 - a}\)
\(\dfrac{-6}{\sqrt{5} - 1}\)
\(\dfrac{-6}{\sqrt{7} + 2}\)
- Contestar
-
\(-2(\sqrt{7} - 2)\)
\(\dfrac{3}{\sqrt{3} - \sqrt{2}}\)
\(\dfrac{4}{\sqrt{6} + \sqrt{2}}\)
- Contestar
-
\(\sqrt{6} - \sqrt{2}\)
\(\dfrac{\sqrt{5}}{\sqrt{8} - \sqrt{6}}\)
\(\dfrac{\sqrt{12}}{\sqrt{12} - \sqrt{8}}\)
- Contestar
-
\(3 + \sqrt{6}\)
\(\dfrac{\sqrt{7x}}{2 - \sqrt{5x}}\)
\(\dfrac{\sqrt{6y}}{1 + \sqrt{3y}}\)
- Contestar
-
\(\dfrac{\sqrt{6y} - 3y\sqrt{2}}{1 - 3y}\)
\(\dfrac{\sqrt{2}}{\sqrt{3} - \sqrt{2}}\)
\(\dfrac{\sqrt{a}}{\sqrt{a} + \sqrt{b}}\)
- Contestar
-
\(\dfrac{a - \sqrt{ab}}{a - b}\)
\(\dfrac{\sqrt{8^3b^5}}{4 - \sqrt{2ab}}\)
\(\dfrac{\sqrt{7x}}{\sqrt{5x} + \sqrt{x}}\)
- Contestar
-
\(\dfrac{\sqrt{35} - \sqrt{7}}{4}\)
\(\dfrac{\sqrt{3y}}{\sqrt{2y} - \sqrt{y}}\)
Ejercicios para la revisión
Simplificar\(x^8y^7 \dfrac{x^4y^8}{x^3y^4}\)
- Contestar
-
\(x^9y^{11}\)
Resolver la desigualdad compuesta\(-8 \le 7 - 5x \le -23\)
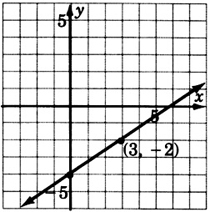
Construye la gráfica de\(y = \dfrac{2}{3}x - 4\)
- Contestar
-
El símbolo\(\sqrt{x}\) representa qué raíz cuadrada del número\(x, x \ge 0\)?
Simplificar\(\sqrt{a^2 + 8a + 16}\)
- Contestar
-
\(a + 4\)


