1.1: Números reales y la línea numérica

HABILIDADES PARA DESARROLLAR

• Construye una recta numérica y grafica puntos sobre ella.
• Utilice una línea numérica para determinar el orden de los números reales.
• Determinar lo contrario de un número real.
• Determinar el valor absoluto de un número real.

Definiciones

Un conjunto es una colección de objetos, normalmente agrupados dentro de llaves\(\{\)\(\}\), donde cada objeto se llama un elemento. Por ejemplo,\(\{\text{red, green, blue}\}\) es un conjunto de colores. Un subconjunto es un conjunto que consiste en elementos que pertenecen a un conjunto dado. Por ejemplo,\(\{\text{green, blue}\}\) es un subconjunto del conjunto de colores anterior. Un conjunto sin elementos se llama el conjunto vacío y tiene su propia notación especial,\(\{\)\(\}\) o\(\varnothing\).

Al estudiar matemáticas, nos enfocamos en conjuntos especiales de números. El conjunto de números naturales (o contando), denotados\(\mathbb{N}\), es

\( \{1,2,3,4,5 , \dots \} \quad \color{Cerulean}{Natural\: Numbers} \)

Los tres periodos\((\dots)\) se denominan puntos suspensivos e indica que los números continúan sin límite. El conjunto de números enteros, denotado\(\mathbb{W}\), es el conjunto de números naturales combinados con cero.

\( \{0,1,2,3,4,5 , \dots\} \quad \color{Cerulean}{Whole\: Numbers} \)

El conjunto de enteros, denotado\(\mathbb{Z}\), consiste en números enteros tanto positivos como negativos, así como cero.

\( \{\dots, -3,-2,-1,0,1,2,3 , \dots\} \quad \color{Cerulean}{Integers} \)

Observe que los conjuntos de números naturales y enteros son ambos subconjuntos del conjunto de enteros.

Los números racionales\(\mathbb{Q}\), denotados, se definen como cualquier número de la forma\(\dfrac{a}{b}\), donde\(a\) y\(b\) son enteros y\(b\) es distinto de cero. Los decimales que repiten o terminan son racionales. Por ejemplo,

\(0.7= \frac{7}{10} \quad \text{and} \quad 0. \overline{3} =0.3333 \dots = \frac{1}{3}\)

El conjunto de enteros es un subconjunto del conjunto de números racionales porque cada entero se puede expresar como una relación del entero y\(1\). En otras palabras, cualquier entero puede escribirse sobre\(1\) y puede considerarse un número racional. Por ejemplo,

\(5= \frac{5}{1}\)

Los números irracionales se definen como cualquier número que no se puede escribir como una relación de dos enteros. Los decimales no terminadores que no se repiten son irracionales. Por ejemplo,

\(\pi =3.14159 \dots \quad \text{and} \quad \sqrt{2} = 1.41421 \dots\)

El conjunto de números reales, denotado\(\mathbb{R}\), se define como el conjunto de todos los números racionales combinados con el conjunto de todos los números irracionales. Por lo tanto, todos los números definidos hasta ahora son subconjuntos del conjunto de números reales. En resumen,

Figura\(\PageIndex{1}\): Números reales

Línea de números

Una línea numérica real, o simplemente una línea numérica, nos permite mostrar visualmente números reales asociándolos con puntos únicos en una línea. El número real asociado a un punto se denomina coordenada. Un punto en la recta numérica real que está asociado a una coordenada se llama su gráfica.

Para construir una recta numérica, dibuje una línea horizontal con flechas en ambos extremos para indicar que continúa sin límite. A continuación, elija cualquier punto para representar el número cero; este punto se llama origen.

Figura\(\PageIndex{2}\)

Marque longitudes consistentes en ambos lados del origen y etiquete cada marca para definir la escala. Los números reales positivos se encuentran a la derecha del origen y los números reales negativos a la izquierda. El número cero no\((0)\) es ni positivo ni negativo. Normalmente, cada tick representa una unidad.

Figura\(\PageIndex{3}\)

Como se ilustra a continuación, la báscula no necesita ser siempre una unidad. En la primera línea numérica, cada marca de verificación representa dos unidades. En el segundo, cada marca representa\(\frac{1}{7}\) de una unidad.

Figura\(\PageIndex{4}\)

El gráfico de cada número real se muestra como un punto en el punto apropiado de la recta numérica. A\(\mathbb{Z}\) continuación se muestra una gráfica parcial del conjunto de números enteros:

Figura\(\PageIndex{5}\)

Ejemplo\(\PageIndex{1}\)

Grafica el siguiente conjunto de números reales:

Solución

Grafica los números en una recta numérica con una escala donde cada marca representa\(\frac{1}{2}\) una unidad.

Figura\(\PageIndex{6}\)

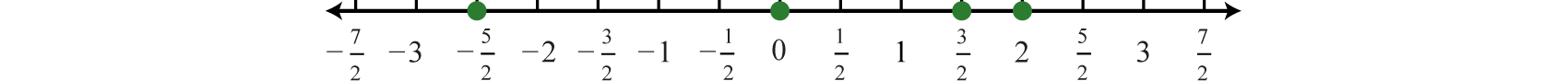
Pedido de números reales

Al comparar números reales en una recta numérica, el número mayor siempre estará a la derecha del más pequeño. Está claro que\(15\) es mayor que\(5\), pero puede que no sea tan claro ver que\(−1\) es mayor que\(−5\) hasta que graficemos cada número en una recta numérica.

Figura\(\PageIndex{7}\)

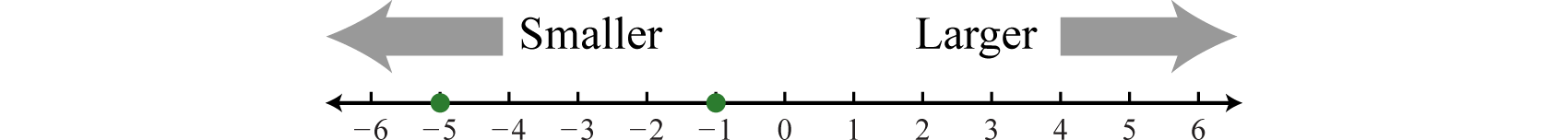
Utilizamos símbolos para ayudarnos a comunicar de manera eficiente las relaciones entre los números en la línea numérica. Los símbolos utilizados para describir una relación de igualdad entre números siguen:

\[\begin{align*} &= \quad \color{Cerulean}{is\ equal\ to} \\ &\neq \quad \color{Cerulean}{is\ not\ equal\ to} \\ &\approx \quad \color{Cerulean}{is\ approximately\ equal\ to} \end{align*}\]

Estos símbolos se utilizan e interpretan de la siguiente manera:

\[\begin{align*} &5=5 \qquad &&\color{Cerulean}{5\ is\ equal\ to\ 5} \\ &0 \neq 5 \qquad &&\color{Cerulean}{0\ is\ not\ equal\ to\ 5} \\ &\pi \approx 3.14 \quad &&\color{Cerulean}{pi\ is\ approximately\ equal\ to\ 3.14} \end{align*}\]

A continuación definimos símbolos que denotan una relación de orden entre números reales.

\[\begin{align*} &< \quad \color{Cerulean}{Less\ than} \\ &> \quad \color{Cerulean}{Greater\ than} \\ &\leq \quad \color{Cerulean}{Less\ than\ or\ equal\ to} \\ &\geq \quad \color{Cerulean}{Greater\ than\ or\ equal\ to} \end{align*}\]

Estos símbolos nos permiten comparar dos números. Por ejemplo,

Dado que la gráfica de\(−120\) está a la izquierda de la gráfica de\(–10\) en la recta numérica, ese número es menor que\(−10\). Podríamos escribir una declaración equivalente de la siguiente manera:

De igual manera, dado que la gráfica de cero se encuentra a la derecha de la gráfica de cualquier número negativo en la recta numérica, cero es mayor que cualquier número negativo.

Los símbolos\(<\) y\(>\) se utilizan para denotar desigualdades estrictas, y los símbolos y se utilizan para denotar desigualdades inclusivas. En algunas situaciones, se puede aplicar correctamente más de un símbolo. Por ejemplo, las dos afirmaciones siguientes son verdaderas:

Además, el componente “o igual a” de una desigualdad inclusiva nos permite escribir correctamente lo siguiente:

El uso lógico de la palabra “o” requiere que sólo una de las condiciones tenga que ser cierta: el “menor que” o el “igual a”.

Ejemplo\(\PageIndex{2}\)

Rellene el espacio en blanco con\(<, =\), o\(>: −2\) ____\(−12\).

Solución

Use > porque la gráfica de\(−2\) está a la derecha de la gráfica de\(−12\) en una recta numérica. Por lo tanto\(−2 > −12\),, que dice “negativo dos es mayor que negativo doce”.

Figura\(\PageIndex{8}\)

Respuesta:

\(-2>-12\)

En este texto, a menudo señalaremos la notación equivalente utilizada para expresar cantidades matemáticas electrónicamente usando los símbolos estándar disponibles en un teclado. Comenzamos con la notación textual equivalente para las desigualdades:

\[\begin{align*} &\geq &&">=" \\ &\leq &&"<=" \\ &\neq &&"!=" \end{align*}\]

Muchas calculadoras, sistemas de álgebra computacional y lenguajes de programación utilizan esta notación.

Opuestos

Lo contrario de cualquier número real\(a\) es\(−a\). Los números reales opuestos están a la misma distancia del origen en una recta numérica, pero sus gráficas se encuentran en lados opuestos del origen y los números tienen signos opuestos.

Figura\(\PageIndex{9}\)

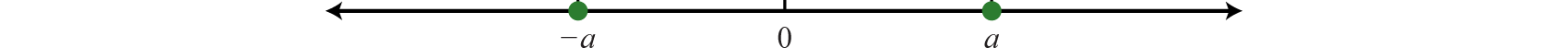
Por ejemplo, decimos que lo contrario de\(10\) es\(−10\).

A continuación, considere lo contrario de un número negativo. Dado el entero\(−7\), el entero a la misma distancia del origen y con el signo opuesto es\(+7\), o simplemente\(7\).

Figura\(\PageIndex{10}\)

Por lo tanto, decimos que lo contrario de\(−7\) es\(−(−7) = 7\). Esta idea lleva a lo que a menudo se conoce como la propiedad doble negativa. Para cualquier número real\(a\),

\(-(-a)=a\)

Ejemplo\(\PageIndex{3}\)

¿De qué es lo contrario\(-\frac{3}{4}\)?

Solución

Aquí aplicamos la propiedad doble negativa.

\(-(-\frac{3}{4})=\frac{3}{4}\)

Ejemplo\(\PageIndex{4}\)

Simplificar\(-(-(4))\)

Solución

Comience con los paréntesis más internos encontrando lo contrario de\(+4\).

\[\begin{align*} -(-(4)) &= -(\color{Cerulean}{-(4)} \color{Black}{)} \\ &= -(\color{Cerulean}{-4} \color{Black}{)} \\ &=4 \end{align*}\]

Contestar

4

Ejemplo\(\PageIndex{5}\)

Simplificar:\(-(-(-2))\).

Solución

Aplicar la propiedad doble-negativo comenzando por los paréntesis más internos.

\[\begin{align*} -(-(-2)) &= -(\color{Cerulean}{-(-2)} \color{Black}{)} \\ &= -(\color{Cerulean}{2} \color{Black}{)} \\ &=-2 \end{align*}\]

Contestar

-2

propina

Si hay un número par de signos negativos consecutivos, entonces el resultado es positivo. Si hay un número impar de signos negativos consecutivos, entonces el resultado es negativo.

¡Prueba esto!

Ejercicio\(\PageIndex{1}\)

Simplificar:\(-(-(-(5)))\).

Contestar

-5

Procedimiento:

\[\begin{align*} -(-(-(5))) &= -(\color{Cerulean}{-(-(5))} \color{Black}{)}\\ &= -(\color{Cerulean}{-(-5)} \color{Black}{)} \\ &= -(\color{Cerulean}{5} \color{Black}{)} \\&= -5 \end{align*} \]

Solución de video:

(haga clic para ver el video)

Valor Absoluto

El valor absoluto de un número real\(a\), denotado\(|a|\), se define como la distancia entre cero (el origen) y la gráfica de ese número real en la recta numérica. Al ser una distancia, siempre es positiva. Por ejemplo,

\(|-4|=4 \quad \text{and} \quad |4|=4\)

Ambos\(4\) y\(−4\) son cuatro unidades del origen, como se ilustra a continuación:

Figura\(\PageIndex{11}\)

Ejemplo\(\PageIndex{6}\)

Simplificar:

a.\(|-12|\)

b.\(|12|\)

Solución

Ambos\(−12\) y\(12\) son doce unidades del origen en una recta numérica. Por lo tanto,

\(|-12|=12 \quad \text{and} \quad |12|=12\)

Contestar

a.\(12\) b.\(12\)

Además, cabe señalar que

\(|0|=0\)

El valor absoluto se puede expresar textualmente usando la notación abs\((a)\). A menudo nos encontramos con valores absolutos negativos, como\(−|3|\) o\(−\) abs\((3)\). Observe que el signo negativo está delante del símbolo de valor absoluto. En este caso, trabajar primero el valor absoluto y luego encontrar lo contrario del resultado.

Trate de no confundir esto con la propiedad doble-negativa, que establece que\(−(−7)=+7\).

Ejemplo\(\PageIndex{7}\)

Simplfy:\(-|-(-7)|\).

Solución

Primero, encuentra lo contrario de\(−7\) dentro del valor absoluto. Entonces encuentra lo contrario del resultado.

\[\begin{align*} -|\color{Cerulean}{-(-7)} \color{Black}{|} &= -|\color{Cerulean}{7} \color{Black}{|} \\ &=-7 \end{align*}\]

Contestar

-7

En este punto, podemos determinar qué números reales tienen un valor absoluto particular. Por ejemplo,

\(|?|=5\)

Piense en un número real cuya distancia al origen sean\(5\) unidades. Hay dos soluciones: la distancia a la derecha del origen y la distancia a la izquierda del origen, a saber,\(\{\pm 5\}\). El símbolo\( (\pm) \) se lee “más o menos” e indica que hay dos respuestas, una positiva y otra negativa.

\(|-5|=5\ \quad \text{and} \quad |5|=5\)

Ahora considere lo siguiente:

\(|?|=-5\)

Aquí deseamos encontrar un valor para el cual la distancia al origen sea negativa. Dado que la distancia negativa no está definida, esta ecuación no tiene solución. Si una ecuación no tiene solución, decimos que la solución es el conjunto vacío:\(\varnothing\).

Claves para llevar

• Cualquier número real se puede asociar con un punto en una línea.
• Crear una línea numérica identificando primero el origen y marcando una escala apropiada para el problema dado.
• Los números negativos se encuentran a la izquierda del origen y los números positivos a la derecha.
• Los números más pequeños siempre se encuentran a la izquierda de los números más grandes en la línea numérica.
• Lo contrario de un número positivo es negativo y lo contrario de un número negativo es positivo.
• El valor absoluto de cualquier número real es siempre positivo porque se define como la distancia desde cero (el origen) en una recta numérica.
• El valor absoluto de cero es cero.

Ejercicio\(\PageIndex{2}\)

Utilice la notación de conjunto para enumerar los elementos descritos.

1. Las horas en un reloj.
2. Los días de la semana.
3. Los primeros diez números enteros.
4. Los primeros diez números naturales.
5. Los primeros cinco enteros pares positivos.
6. Los primeros cinco enteros impares positivos.

Contestar

1. \(\{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12\}\)

3. \(\{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}\)

5. \(\{2, 4, 6, 8, 10\}\)

Ejercicio\(\PageIndex{3}\)

Determinar si los siguientes números reales son enteros, racionales o irracionales.

1. \(12\)
2. \(−3\)
3. \(4.5\)
4. \(−5\)
5. \(0.3 \overline{6} \)
6. \(0. \overline{3} \)
7. \(1.001000100001 \dots\)
8. \(1.00 \overline{1} \)
9. \(e=2.71828 \dots \)
10. \(\sqrt{7}=2.645751 \dots \)
11. \(−7\)
12. \(3.14\)
13. \(227\)
14. \(1.33\)
15. \(0\)
16. \(8,675,309\)

Contestar

1: Entera, Racional

3: Racional

5: Racional

7: Irracional

9: Irracional

11: Entero, Racional

13: Racional

15: Entero, Racional

Ejercicio\(\PageIndex{4}\)

Verdadero o falso.

1. Todos los enteros son números racionales.
2. Todos los enteros son números enteros.
3. Todos los números racionales son números enteros.
4. Algunos números irracionales son racionales.
5. Todos los números decimales de terminación son racionales.
6. Todos los números irracionales son reales.

Contestar

1: Cierto

3: Falso

5: Cierto

Ejercicio\(\PageIndex{5}\)

Elija una escala apropiada y grafique los siguientes conjuntos de números reales en una recta numérica.

1. \(\{−3, 0, 3\}\)
2. \(\{−2, 2, 4, 6, 8, 10\}\)
3. \(\{−2, −1/3, 2/3, 5/3\}\)
4. \(\{−5/2, −1/2, 0, 1/2 , 2\}\)
5. \(\{−5/7, 0, 2/7 , 1\}\)
6. \(\{ –5, –2, –1, 0\}\)
7. \(\{ −3, −2, 0, 2, 5\}\)
8. \(\{−2.5, −1.5, 0, 1, 2.5\}\)
9. \(\{0, 0.3, 0.6, 0.9, 1.2\}\)
10. \(\{−10, 30, 50\}\)
11. \(\{−6, 0, 3, 9, 12\}\)
12. \(\{−15, −9, 0, 9, 15\}\)

Contestar

1. \(\{−3, 0, 3\}\)

Figura\(\PageIndex{12}\)

3. \(\{−2, −1/3, 2/3, 5/3\}\)

Figura\(\PageIndex{13}\)

5. \(\{−5/7, 0, 2/7 , 1\}\)

Figura\(\PageIndex{14}\)

7. \(\{ −3, −2, 0, 2, 5\}\)

Figura\(\PageIndex{15}\)

9. \(\{0, 0.3, 0.6, 0.9, 1.2\}\)

Figura\(\PageIndex{16}\)

11. \(\{−6, 0, 3, 9, 12\}\)

Figura\(\PageIndex{17}\)

Ejercicio\(\PageIndex{6}\)

Rellene el espacio en blanco con\(<, =\), o\(>\).

1. \(−7\)___\(0\)
2. \(30\)___\(2\)
3. \(10\)___\(−10\)
4. \(−150\)___\(−75\)
5. \(−0.5\)___\(−1.5\)
6. \(0\)___\(0\)
7. \(-500\)___\(200\)
8. \(−1\)___\(−200\)
9. \(−10\)___\(−10\)
10. \(−40\)___\(−41\)

Contestar

1. \(<\)

3. \(>\)

5. \(>\)

7. \(<\)

9. \(=\)

Ejercicio\(\PageIndex{7}\)

Verdadero o falso.

1. \(5≠7\)
2. \(4=5\)
3. \(1≠1\)
4. \(−5>−10\)
5. \(4 \leq 4\)
6. \(−12 \geq 0\)
7. \(−10=−10\)
8. \(3>3\)
9. \(−1000<−20\)
10. \(0=0\)

Contestar

1. Cierto

3. Falso

5. Cierto

7. Cierto

9. Cierto

Ejercicio\(\PageIndex{8}\)

Enumere los números.

1. Enumere tres enteros menores que\(−5\).
2. Enumere tres enteros mayores que\(−10\).
3. Enumere tres números racionales menores que cero.
4. Enumere tres números racionales mayores a cero.
5. Enumere tres enteros entre\(−20\) y\(−5\).
6. Enumere tres números racionales entre\(0\) y\(1\).

Contestar

1. \(−10, −7, −6\)(las respuestas pueden variar)

3. \(−1, −2/3, −1/3\)(las respuestas pueden variar)

5. \(−15, −10, −7\)(las respuestas pueden variar)

Ejercicio\(\PageIndex{9}\)

Traduce cada declaración a una oración en inglés.

1. \(10<20\)
2. \(−50 \leq −10\)
3. \(−4 \neq 0\)
4. \(30 \geq −1\)
5. \(0=0\)
6. \(e \approx 2.718\)

Contestar

1. Diez es menos de veinte.

3. Negativo cuatro no es igual a cero.

5. Cero es igual a cero.

Ejercicio\(\PageIndex{10}\)

Traducir lo siguiente en una declaración matemática.

1. Siete negativo es menor que cero.
2. Veinticuatro no es igual a diez.
3. Cero es mayor o igual a uno negativo.
4. Cuatro es mayor o igual a veintiuno negativo.
5. Dos negativos es igual a dos negativos.
6. Negativo dos mil es menos que negativo mil.

Contestar

1. \(−7<0\)

3. \(0 \geq −1\)

5. \(−2=−2\)

Ejercicio\(\PageIndex{11}\)

Simplificar.

1. \(−(−9)\)
2. \(−(−35)\)
3. \(−(10)\)
4. \(−(3)\)
5. \(−(5)\)
6. \(−(34)\)
7. \(−(−1)\)
8. \(−(−(−1))\)
9. \(−(−(1))\)
10. \(−(−(−3))\)
11. \(−(−(−(−11)))\)

Contestar

1. \(9\)

3. \(−10\)

5. \(−5\)

7. \(1\)

9. \(1\)

11. \(11\)

Ejercicio\(\PageIndex{12}\)

Contesta las siguientes preguntas.

1. ¿Qué es lo contrario de\(-12\)
2. ¿De qué es lo contrario\(\pi \)?
3. ¿Qué es lo contrario\(−0.01\)?
4. ¿Es lo contrario de\(−12\) más pequeño o mayor que\(−11\)?
5. ¿Es lo contrario de\(7\) más pequeño o mayor que\(−6\)?

Contestar

2. \(-\pi \)

4. Más grande

Ejercicio\(\PageIndex{13}\)

Rellene el espacio en blanco con\(<, =\), o\(>\).

1. \(−7\)___\(−(−8)\)
2. \(6\)___\(−(6)\)
3. \(13\)___\(−(−12)\)
4. \(−(−5)\)___\(−(−2)\)
5. \(−100\)___\(−(−(−50))\)
6. \(44\)___\(−(−44)\)

Contestar

1. \(<\)

3. \(>\)

5. \(<\)

Ejercicio\(\PageIndex{14}\)

Simplificar.

1. \(|20|\)
2. \(|−20|\)
3. \(|−33|\)
4. \(|−0.75|\)
5. \(|−\frac{3}{5}|\)
6. \(|38|\)
7. \(|0|\)
8. \(|1|\)
9. \(−|12|\)
10. \(−|−20|\)
11. \(−|20|\)
12. \(−|−8|\)
13. \(−|7|\)
14. \(−|−316|\)
15. \(−(−|\frac{8}{9}|)\)
16. \(|−(−2)|\)
17. \(−|−(−3)|\)
18. \(−(−|5|)\)
19. \(−(−|−45|)\)
20. \(−|−(−21)|\)
21. abs\((6)\)
22. abs\((−7)\)
23. \(−\)abs\((5)\)
24. \(−\)abs\((−19)\)
25. \(−(−\)abs\((9))\)
26. \(−\)abs\((−(−12))\)

Contestar

1. \(20\)

3. \(33\)

5. \(\frac{3}{5}\)

7. \(0\)

9. \(−12\)

11. \(−20\)

13. \(−7\)

15. \(\frac{8}{9}\)

17. \(−3\)

19. \(45\)

21. \(6\)

23. \(−5\)

25. \(9\)

Ejercicio\(\PageIndex{15}\)

Determinar lo desconocido.

1. \(| ? |=9\)
2. \(| ? |=15\)
3. \(| ? |=0\)
4. \(| ? |=1\)
5. \(| ? |=−8\)
6. \(| ? |=−20\)
7. \(|?|−10=−2\)
8. \(|?|+5=14\)

Contestar

1. \(\pm 9\)

3. \(0\)

5. \(\varnothing\), Sin solución

7. \(\pm 8\)

Ejercicio\(\PageIndex{16}\)

Rellene el espacio en blanco con\(<, =\), o\(>\).

1. \(|−2|\)____\(0\)
2. \(|−7|\)____\(|−10|\)
3. \(−10\)____\(−|−2|\)
4. \(|−6|\)____\(|−(−6)|\)
5. \(−|3|\)____\(|−(−5)|\)
6. \(0\)____\(−|−(−4)|\)

Contestar

1. \(>\)

3. \(<\)

5. \(<\)

Ejercicio\(\PageIndex{17}\)

Temas de Mesa de Discusión.

1. Investigar y discutir la historia del número cero.
2. Investigar y discutir los diversos sistemas de numeración a lo largo de
3. Investigar y discutir la definición e historia de\(\pi\).
4. Investigar la historia de los números irracionales. ¿A quién se le atribuye probar que la raíz cuadrada de\(2\) es irracional y qué le pasó?
5. Investigar y discutir la historia del valor absoluto.
6. Discutir la definición de “solo hazlo positivo” de valor absoluto