2.7: Introducción a las desigualdades y a la notación de intervalos

Objetivos de aprendizaje

• Grafique las soluciones de una sola desigualdad en una recta numérica y exprese las soluciones usando notación de intervalos.
• Grafique las soluciones de una desigualdad compuesta en una recta numérica y exprese las soluciones usando notación de intervalos.

Intervalos no acotados

Una desigualdad algebraica, tal como\(x≥2\), se lee “\(x\)es mayor o igual a”\(2\). Esta desigualdad tiene infinitamente muchas soluciones para\(x\). Algunas de las soluciones son\(2, 3, 3.5, 5, 20,\) y\(20.001\). Dado que es imposible enumerar todas las soluciones, se necesita un sistema que permita una comunicación clara de este conjunto infinito. Dos formas comunes de expresar soluciones a una desigualdad son graficándolas en una recta numérica y usando notación de intervalo.

Para expresar la solución gráficamente, dibuje una recta numérica y sombree en todos los valores que son soluciones a la desigualdad. La notación de intervalo es textual y utiliza la notación específica de la siguiente manera:

Figura\(\PageIndex{1}\)

Determine la notación del intervalo después de graficar el conjunto de soluciones en una recta numérica. Los números en notación de intervalos deben escribirse en el mismo orden en que aparecen en la recta numérica, con números más pequeños en el conjunto apareciendo primero. En este ejemplo, existe una desigualdad inclusiva, lo que significa que el límite inferior 2 se incluye en la solución. Denote esto con un punto cerrado en la recta numérica y un corchete en notación de intervalo. El símbolo (∞) se lee como infinito e indica que el conjunto no está acotado a la derecha en una recta numérica. La notación de intervalos requiere un paréntesis para encerrar el infinito. El corchete indica que el límite está incluido en la solución. Los paréntesis indican que el límite no está incluido. El infinito es un límite superior a los números reales, pero no es en sí mismo un número real: no puede incluirse en el conjunto de soluciones.

Ahora compare la notación de intervalo en el ejemplo anterior con la de la desigualdad estricta, o no inclusiva, que sigue:

Figura\(\PageIndex{2}\)

Las desigualdades estrictas implican que las soluciones pueden llegar muy cerca del punto límite, en este caso 2, pero en realidad no incluirlo. Denote esta idea con un punto abierto en la recta numérica y un paréntesis redondo en notación de intervalo.

Ejemplo\(\PageIndex{1}\)

Gráfica y da la notación de intervalo equivalente:

\(x<3\).

Solución:

Use un punto abierto en\(3\) y sombree todos los números reales estrictamente menos de\(3\). Use infinito negativo\((−∞)\) para indicar que el conjunto de soluciones no está acotado a la izquierda en una recta numérica.

Figura\(\PageIndex{3}\)

Respuesta:

Notación de intervalos:\((-∞, 3)\)

Ejemplo\(\PageIndex{2}\)

Gráfica y da la notación de intervalo equivalente:

\(x≤5\).

Solución:

Use un punto cerrado y sombree todos los números menores que e incluyendo 5.

Figura\(\PageIndex{4}\)

Respuesta:

Notación de intervalos:\((−∞, 5]\)

Es importante ver que\(5≥x\) es lo mismo que\(x≤5\). Ambos requieren valores\(x\) de ser menores o iguales a\(5\). Para evitar confusiones, es una buena práctica reescribir todas las desigualdades con la variable de la izquierda. Además, al usar texto, usa “inf” como una forma abreviada de infinito. Por ejemplo, se\((−∞, 5]\) puede expresar textualmente como\((−\) inf,\(5]\).

Una desigualdad compuesta es en realidad dos o más desigualdades en una declaración unidas por la palabra “y” o por la palabra “o”. Las desigualdades compuestas con el lógico “o” requieren que se satisfagan cualquiera de las dos condiciones. Por lo tanto, el conjunto de soluciones de este tipo de desigualdad compuesta consiste en todos los elementos de los conjuntos de solución de cada desigualdad. Cuando nos unimos a estos conjuntos de soluciones individuales se llama la unión, denotada\(∪\). Por ejemplo, las soluciones a la desigualdad compuesta\(x<3\) o se\(x≥6\) pueden graficar de la siguiente manera:

Figura\(\PageIndex{5}\)

A veces nos encontramos con desigualdades compuestas donde los conjuntos de soluciones separadas se superponen. En el caso en que la desigualdad compuesta contenga la palabra “o”, combinamos todos los elementos de ambos conjuntos para crear un conjunto que contenga todos los elementos de cada uno.

Ejemplo\(\PageIndex{3}\)

Gráfica y da la notación de intervalo equivalente:

\(x≤−1\)o\(x<3\).

Solución:

Combina todas las soluciones de ambas desigualdades. Las soluciones a cada desigualdad se esbozan por encima de la recta numérica como medio para determinar la unión, la cual se grafica en la recta numérica a continuación.

Figura\(\PageIndex{6}\)

Respuesta:

Notación de intervalos:\((−∞, 3)\)

Cualquier número real menor que\(3\) en la región sombreada en la línea numérica satisfará al menos una de las dos desigualdades dadas.

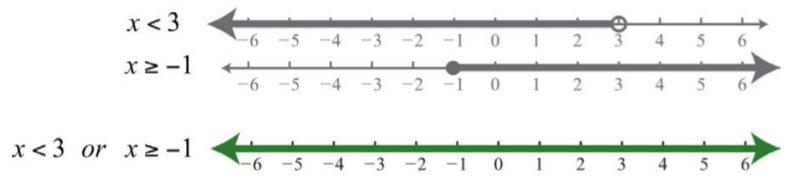
Ejemplo\(\PageIndex{4}\)

Gráfica y da la notación de intervalo equivalente:

\(x<3\)o\(x≥−1\).

Solución:

Ambos conjuntos de soluciones están graficados por encima de la unión, que se grafica a continuación.

Figura\(\PageIndex{7}\)

Respuesta:

Notación de intervalos:\(R = (−∞, ∞)\)

Cuando combinas ambos conjuntos de soluciones y formas la unión, puedes ver que todos los números reales satisfacen la desigualdad compuesta original.

En resumen,

Figura\(\PageIndex{8}\)

Figura\(\PageIndex{9}\)

y

Figura\(\PageIndex{10}\)

Figura\(\PageIndex{11}\)

Intervalos acotados

Una desigualdad como

\(-1\leq x<3\)

dice “\(−1\)uno es menor o igual a\(x\) y\(x\) es menor que tres”. Esta es una desigualdad compuesta porque se puede descomponer de la siguiente manera:

\(-1\leq x\)y\(x<3\)

El lógico “y” requiere que ambas condiciones sean ciertas. Ambas desigualdades son satisfechas por todos los elementos en la intersección, denotados\(∩\), de los conjuntos de solución de cada uno.

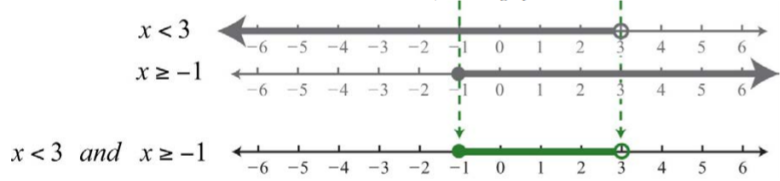
Ejemplo\(\PageIndex{5}\)

Gráfica y da la notación de intervalo equivalente:

\(x<3\)y\(x≥−1\).

Solución:

Determinar la intersección, o superposición, de los dos conjuntos de soluciones. Las soluciones a cada desigualdad se esbozan por encima de la recta numérica como medio para determinar la intersección, la cual se grafica en la recta numérica de abajo.

Figura\(\PageIndex{12}\)

Aquí no\(x=3\) hay una solución porque solo resuelve una de las desigualdades.

Respuesta:

Notación de intervalos:\([−1, 3)\)

Alternativamente, podemos interpretar\(−1≤x<3\) como todos los valores posibles para\(x\) entre o delimitados por\(−1\) y\(3\) en una recta numérica. Por ejemplo, una de esas soluciones es\(x=1\). Observe que\(1\) está entre\(−1\) y\(3\) en una recta numérica, o eso\(−1 < 1 < 3\). De igual manera, podemos ver que otras posibles soluciones son\(−1, −0.99, 0, 0.0056, 1.8\), y\(2.99\). Dado que hay infinitamente muchos números reales entre\(−1\) y\(3\), debemos expresar la solución gráficamente y/o con notación de intervalos, en este caso\([−1, 3)\).

Ejemplo\(\PageIndex{6}\)

Gráfica y da la notación de intervalo equivalente:

\(−\frac{3}{2}<x<2\).

Solución:

Sombra todos los números reales delimitados por, o estrictamente entre,\(−\frac{3}{2}=−1\frac{1}{2}\) y\(2\).

Figura\(\PageIndex{13}\)

Respuesta:

Notación de intervalos:\((−\frac{3}{2}, 2)\)

Ejemplo\(\PageIndex{7}\)

Gráfica y da la notación de intervalo equivalente:

\(−5<x\leq 15\)

Solución:

Sombra todos los números reales entre\(−5\) y\(15\), e indique que el límite superior,\(15\), se incluye en el conjunto de soluciones mediante el uso de un punto cerrado.

Figura\(\PageIndex{14}\)

Respuesta:

Notación de intervalos:\((−5, 15]\)

En los dos ejemplos anteriores, no descomponíamos las desigualdades, sino que optamos por pensar en todos los números reales entre los dos límites dados.

En resumen,

Figura\(\PageIndex{15}\)

Notación de Set-Builder

En este texto, utilizamos la notación de intervalos. Sin embargo, otros recursos que es probable que encuentre utilizan un método alternativo para describir conjuntos llamado notación set-builder. Hemos utilizado la notación set para enumerar los elementos como los enteros

\(\{...,-3,-2,-1,0,1,2,3,...\}\)

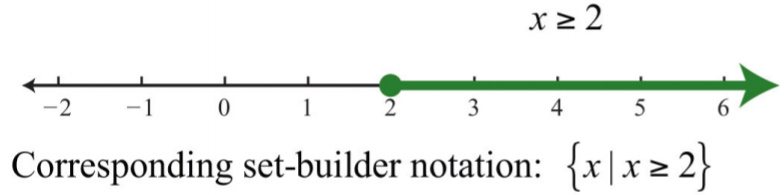
Las llaves agrupan los elementos del conjunto y las marcas de puntos suspensivos indican que los enteros continúan para siempre. En esta sección, queremos describir intervalos de números reales, por ejemplo, los números reales mayores o iguales a\(2\).

Figura\(\PageIndex{16}\)

Dado que el conjunto es demasiado grande para enumerarlo, la notación set-builder nos permite describirlo usando notación matemática familiar. A continuación se muestra un ejemplo de notación de constructor de conjuntos:

\(\{ x∈\mathbb{R} | x\geq 2\}\)

Aquí\(x∈R\) se describe el tipo de número, donde\((∈)\) se lee el símbolo “elemento de”. Esto implica que la variable\(x\) representa un número real. La barra vertical\((|)\) se lee “tal que”. Por último, la sentencia\(x≥2\) es la condición que describe el conjunto usando notación matemática. En este punto de nuestro estudio del álgebra, se supone que todas las variables representan números reales. Por ello, se puede omitir el “\(∈R\)” y escribir\(\{x|x≥2\}\), que se lee “el conjunto de todos los números reales\(x\) tal que\(x\) sea mayor o igual a”\(2\).

Figura\(\PageIndex{17}\)

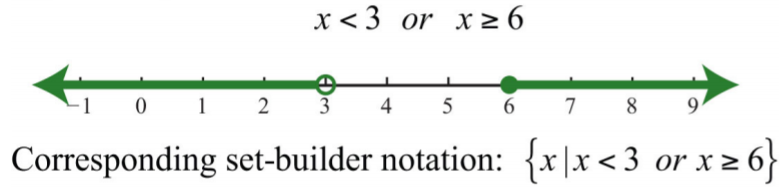
Para describir desigualdades compuestas como\(x<3\) o\(x≥6\), escribir\(\{x|x<3\) o\(x≥6\}\), que se lee “el conjunto de todos los números reales\(x\) tal que\(x\) sea menor que\(3\) o\(x\) sea mayor que o igual a”\(6\).

Figura\(\PageIndex{18}\)

Escribir intervalos acotados, como\(−1≤x<3\), como\(\{x|−1≤x<3\}\), que se lee “el conjunto de todos los números reales\(x\) tal que\(x\) es mayor o igual a\(−1\) y menor que”\(3\).

Claves para llevar

• Las desigualdades suelen tener infinitamente muchas soluciones, así que en lugar de presentar una lista imposiblemente grande, presentamos tales conjuntos de soluciones ya sea gráficamente en una línea numérica o textualmente usando notación de intervalo.
• Las desigualdades inclusivas con el componente “o igual a” se indican con un punto cerrado en la recta numérica y con corchete usando notación de intervalo.
• Las desigualdades estrictas sin el componente “o igual a” se indican con un punto abierto en la recta numérica y un paréntesis usando notación de intervalo.
• Las desigualdades compuestas que hacen uso del “o” lógico se resuelven mediante soluciones de cualquiera de las dos desigualdades. El conjunto de soluciones es la unión de cada conjunto de soluciones individuales.
• Las desigualdades compuestas que hacen uso de la lógica “y” requieren que todas las desigualdades se resuelvan con una sola solución. El conjunto de soluciones es la intersección de cada conjunto de soluciones individuales.
• Las desigualdades compuestas de la forma se\(n<A<m\) pueden descomponer en dos desigualdades usando el lógico “y”. No obstante, es igual de válido considerar que el argumento\(A\) esté delimitado entre los valores\(n\) y\(m\).

Ejercicio\(\PageIndex{1}\) Simple Inequalities

Grafique todas las soluciones en una recta numérica y proporcione la notación de intervalo correspondiente.

1. \(x≤10\)
2. \(x>−5\)
3. \(x>0\)
4. \(x≤0\)
5. \(x≤−3\)
6. \(x≥−1\)
7. \(−4<x\)
8. \(1≥x\)
9. \(x<−\frac{1}{2}\)
10. \(x≥−\frac{3}{2}\)
11. \(x≥−1\frac{3}{4}\)
12. \(x<\frac{3}{4}\)

Contestar

1. \((−∞, 10]\)

Figura\(\PageIndex{19}\)

3. \((0, ∞)\)

Figura\(\PageIndex{20}\)

5. \((−∞, −3]\)

Figura\(\PageIndex{21}\)

7. \((−4, ∞)\)

Figura\(\PageIndex{22}\)

9. \((−∞, −\frac{1}{2})\)

Figura\(\PageIndex{23}\)

11. \([−1\frac{3}{4}, ∞)\)

Figura\(\PageIndex{24}\)

Ejercicio\(\PageIndex{2}\) Compound Inequalities

Grafique todas las soluciones en una recta numérica y dé la notación de intervalo correspondiente.

1. \(−2<x<5\)
2. \(−5≤x≤−1\)
3. \(−5<x\leq 20\)
4. \(0\leq x<15\)
5. \(10<x\leq 40\)
6. \(-40\leq x<-10\)
7. \(0<x\leq 50\)
8. \(-30<x<0\)
9. \(-\frac{5}{8}<x<\frac{1}{8}\)
10. \(-\frac{3}{4}\leq x\leq \frac{1}{2}\)
11. \(−1≤x<1\frac{1}{2}\)
12. \(−1\frac{1}{2}<x<-\frac{1}{2}\)
13. \(x<-3\)o\(x>3\)
14. \(x<−2\)o\(x≥4\)
15. \(x≤0\)o\(x>10\)
16. \(x≤−20\)o\(x≥−10\)
17. \(x<-\frac{2}{3}\)o\(x>\frac{1}{3}\)
18. \(x≤−\frac{4}{3}\)o\(x>−\frac{1}{3}\)
19. \(x>−5\)o\(x<5\)
20. \(x<12\)o\(x>-6\)
21. \(x<3\)o\(x≥3\)
22. \(x≤0\)o\(x>0\)
23. \(x<−7\)o\(x<2\)
24. \(x≥−3\)o\(x>0\)
25. \(x≥5\)o\(x>0\)
26. \(x<15\)o\(x≤10\)
27. \(x>−2\)y\(x<3\)
28. \(x≥0\)y\(x<5\)
29. \(x≥−5\)y\(x≤−1\)
30. \(x<-4\)y\(x>2\)
31. \(x≤3\)y\( x>3\)
32. \(x≤5\)y\(x≥5\)
33. \(x≤0\)y\( x≥0\)
34. \(x<2\)y\( x≤−1\)
35. \(x>0\)y\( x≥−1\)
36. \(x<5\)y\( x<2\)

Contestar

1. \((−2, 5)\)

Figura\(\PageIndex{25}\)

3. \((−5, 20]\)

Figura\(\PageIndex{26}\)

5. \((10, 40]\)

Figura\(\PageIndex{27}\)

7. \((0, 50]\)

Figura\(\PageIndex{28}\)

9. \((−\frac{5}{8}, \frac{1}{8})\)

Figura\(\PageIndex{29}\)

11. \([−1, 1\frac{1}{2})\)

Figura\(\PageIndex{30}\)

13. \((−∞, −3)∪(3, ∞)\)

Figura\(\PageIndex{31}\)

15. \((−∞, 0]∪(10, ∞)\)

Figura\(\PageIndex{32}\)

17. \((−∞, −\frac{2}{3})∪(\frac{1}{3}, ∞)\)

Figura\(\PageIndex{33}\)

19. \(R\)

Figura\(\PageIndex{34}\)

21. \(R\)

Figura\(\PageIndex{35}\)

23. \((−∞, 2)\)

Figura\(\PageIndex{36}\)

25. \((0, ∞)\)

Figura\(\PageIndex{37}\)

27. \((−2, 3)\)

Figura\(\PageIndex{38}\)

29. \([−5, −1]\)

Figura\(\PageIndex{39}\)

31. \(∅\)

Figura\(\PageIndex{40}\)

33. \(\{0\}\)

Figura\(\PageIndex{41}\)

35. \((0, ∞)\)

Figura\(\PageIndex{42}\)

Ejercicio\(\PageIndex{3}\) Interval Notation

Determinar la desigualdad dadas las respuestas expresadas en notación de intervalos.

1. \((−∞, 7]\)
2. \((−4, ∞)\)
3. \([−\frac{1}{2}, ∞)\)
4. \((−∞, −3)\)
5. \((−8, 10]\)
6. \((−20, 0]\)
7. \((−14, −2)\)
8. \([\frac{2}{3}, \frac{4}{3}]\)
9. \((−\frac{3}{4}, \frac{1}{2})\)
10. \((−∞, −8)\)
11. \((8, ∞)\)
12. \((−∞, 4)∪[8, ∞)\)
13. \((−∞, −2]∪[0, ∞)\)
14. \((−∞, −5]∪(5, ∞)\)
15. \((−∞, 0)∪(2, ∞)\)
16. \((−∞, −15)∪(−5, ∞)\)

Contestar

1. \(x\leq 7\)

3. \(x≥−\frac{1}{2}\)

5. \(−8<x\leq 10\)

7. \(−14<x<-2\)

9. \(-\frac{3}{4}<x<\frac{1}{2}\)

11. \(x>8\)

13. \(x≤−2\)o\(x≥0\)

15. \(x<0\)o\(x>2\)

Ejercicio\(\PageIndex{4}\) Interval Notation

Escribir una desigualdad equivalente.

1. Todos los números reales menores que\(27\).
2. Todos los números reales menores o iguales a cero.
3. Todos los números reales mayores que\(5\).
4. Todos los números reales mayores o iguales a\(−8\).
5. Todos los números reales estrictamente entre\(−6\) y\(6\).
6. Todos los números reales estrictamente entre\(−80\) y\(0\).

Contestar

1. \(x<27\)

3. \(x>5\)

5. \(-6<x<6\)

Ejercicio\(\PageIndex{5}\) Discussion Board Topics

1. Compara la notación de intervalos con la notación set-builder. Comparte un ejemplo de un conjunto descrito usando ambos sistemas.
2. Explique por qué no usamos un corchete en la notación de intervalos cuando infinito es un punto final.
3. Investigar y discutir las diferentes desigualdades compuestas, particularmente uniones e intersecciones.
4. Investigar y discutir la historia del infinito.
5. Investigar y discutir las contribuciones de Georg Cantor.
6. ¿Qué es un diagrama de Venn? Explique y publique un ejemplo.

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar

5. Las respuestas pueden variar