2.8: Desigualdades lineales (una variable)

Última actualización
Guardar como PDF

Page ID: 110131

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Identificar desigualdades lineales y verificar soluciones.
Resolver desigualdades lineales y expresar las soluciones gráficamente en una recta numérica y en notación de intervalos.
Resolver desigualdades lineales compuestas y expresar las soluciones gráficamente en una recta numérica y en notación de intervalos.
Resolver aplicaciones que involucran desigualdades lineales e interpretar los resultados.

Definición de una Desigualdad Lineal

Una desigualdad lineal es una declaración matemática que relaciona una expresión lineal como menor o mayor que otra. A continuación se presentan algunos ejemplos de desigualdades lineales, todas las cuales se resuelven en esta sección:

$3x+7<16\quad -2x+1\geq 21\quad -7(2x+1)<1$

Una solución a una desigualdad lineal es un número real que producirá una declaración verdadera cuando se sustituya por la variable. Las desigualdades lineales tienen infinitamente muchas soluciones o ninguna solución. Si hay infinitamente muchas soluciones, grafique el conjunto de soluciones en una línea numérica y/o exprese la solución usando la notación de intervalos.

Ejemplo$\PageIndex{1}$

¿Son$x=−2$ y$x=4$ soluciones para$3x+7<16$?

Solución:

Sustituir los valores por$x$, simplificar y verificar para ver si obtenemos una declaración verdadera.

$\begin{array}{c|c} {\underline{Check\:x=-2}}&{\underline{Check\:x=4}}\\{\begin{aligned} 3(\color{OliveGreen}{-2}\color{black}{)+7}&<16 \\ -6+7&<16 \\ 1&<16\quad\color{Cerulean}{\checkmark} \end{aligned}}&{\begin{aligned} 3(\color{OliveGreen}{4}\color{black}{)+7}&<16 \\ 12+7&<16 \\ 19&<16\quad\color{red}{x} \end{aligned}} \end{array}$

Respuesta:

$x=-2$es una solución y no$x=4$ lo es.

Álgebra de Desigualdades Lineales

Todas menos una de las técnicas aprendidas para resolver ecuaciones lineales se aplican a la resolución de desigualdades lineales. Puedes sumar o restar cualquier número real a ambos lados de una desigualdad, y puedes multiplicar o dividir ambos lados por cualquier número real positivo para crear desigualdades equivalentes. Por ejemplo,

-5\ color {cerúleo} {-7} &\ color {cerúleo} {Restar\ :7\ :de\ :ambos\ :lados.}\\ 3&>-12\ quad\ color {cerúleo} {\ marca de verificación} &\ color {cerúleo} {Verdadero}\\ 10&>-5\\\ frac {10} {\ color {cerúleo} {5}} >\ frac {-5} {\ color {cerúleo} {5}} &\ color {cerúleo} {Divide\ :ambos\ :lados\ :por\ :5.}\\ 2&>-1\ quad\ color { Cerúleo} {\ marca de verificación} &\ color {cerúleo} {Verdadero}\ final {alineado}\)

Tanto restar$7$ de cada lado como dividir cada lado por$+5$ resultado una desigualdad equivalente que es verdad.

Ejemplo$\PageIndex{2}$

Resuelve y grafica el conjunto de soluciones:

$3x+7<16$.

Solución:

$\begin{aligned} 3x+7&<16 \\ 3x+7\color{Cerulean}{-7}&<16\color{Cerulean}{-7} \\ 3x&<9 \\ \frac{3x}{\color{Cerulean}{3}}&<\frac{9}{\color{Cerulean}{3}} \\ x&<3 \end{aligned}$

$Captura de pantalla (849) .png$

Figura$\PageIndex{1}$

Es útil tomarse un minuto y elegir algunos valores dentro y fuera del conjunto de soluciones, sustituirlos por la desigualdad original y luego verificar los resultados. Como se indicó, se debe$x=0$ esperar resolver la desigualdad original, pero no$x=5$ debe.

$\begin{array}{c|c} {\underline{Check\:x=0}}&{\underline{Check\:x=5}}\\{\begin{aligned} 3(\color{OliveGreen}{0}\color{black}{)+7}&<16 \\ 7&<16\quad\color{Cerulean}{\checkmark} \end{aligned}}&{\begin{aligned} 3(\color{OliveGreen}{5}\color{black}{)+7}&<16 \\ 15+7&<16 \\ 22&<16\quad\color{red}{x} \end{aligned}} \end{array}$

Comprobando de esta manera da un buen indicio de que la desigualdad se soluciona correctamente. Esto se puede hacer mentalmente.

Respuesta:

Notación de intervalos:$(−∞, 3)$

Cuando se trabaja con desigualdades lineales, se aplica una regla diferente al multiplicar o dividir por un número negativo. Para ilustrar el problema, considere la afirmación verdadera$10>−5$ y divida a ambas partes por$−5$.

\ frac {-5} {\ color {cerúleo} {-5}} &\ color {cerúleo} {Divide\ :ambos\ :lados\ :por\ :-5.}\\ -2&\ color {rojo} {>}\ color {negro} {1}\ quad\ color {rojo} {x} &\ color {cerúleo} {Falso}\ final {alineado}\)

Dividir por$−5$ resultados en una declaración falsa. Para conservar una verdadera afirmación, se debe revertir la desigualdad.

$\begin{aligned} 10&\color{OliveGreen}{>}\color{black}{-5} \\ \frac{10}{\color{Cerulean}{-5}}&<\frac{-5}{\color{Cerulean}{-5}} &\color{Cerulean}{Reverse\:the\:inequality.} \\ -2&\color{OliveGreen}{<}\color{black}{1}\quad\color{Cerulean}{\checkmark}&\color{Cerulean}{True} \end{aligned}$

El mismo problema ocurre cuando se multiplica por un número negativo. Esto lleva a la siguiente nueva regla: al multiplicar o dividir por un número negativo, revertir la desigualdad. Es fácil olvidarse de hacer esto así que tenga especial cuidado en estar atento a los coeficientes negativos.

En general, dadas las expresiones algebraicas$A$ y$B$, donde$c$ es un número real positivo distinto de cero, tenemos las siguientes propiedades de desigualdades:

$\begin{array}{ll}{\textbf{Addition property of inequalities:}}&{\text{If }A<B\text{ then, }A\color{Cerulean}{+c}\color{black}{<B}\color{Cerulean}{+c}}\\{\textbf{Subtraction property of inequalities:}}&{\text{If }A<B,\text{ then }A\color{Cerulean}{-c}\color{black}{<B}\color{Cerulean}{-c}}\\{\textbf{Multiplication property of inequalities:}}&{\text{If }A<B,\text{ then }\color{Cerulean}{c}\color{black}{A<}\color{Cerulean}{c}\color{black}{B}}\\{}&{\text{If }A<B,\text{ then }\color{Cerulean}{-c}\color{black}{A}\color{OliveGreen}{>}\color{Cerulean}{-c}\color{black}{B}}\\{\textbf{Division property of inequalities:}}&{\text{If }A<B,\text{ then }\frac{A}{\color{Cerulean}{c}}\color{black}{<\frac{B}{\color{Cerulean}{c}}}}\\{}&{\text{If }A<B,\text{ then }\frac{A}{\color{Cerulean}{-c}}\color{OliveGreen}{>}\color{black}{\frac{B}{\color{Cerulean}{-c}}}} \end{array}$

Utilizamos estas propiedades para obtener una desigualdad equivalente, una con el mismo conjunto de soluciones, donde se aísla la variable. El proceso es similar a resolver ecuaciones lineales.

Ejemplo$\PageIndex{3}$

Resolver:

$−2x+1≥21$.

Solución:

$Captura de pantalla (850) .png$

Figura$\PageIndex{2}$

Respuesta:

Notación de intervalos:$(−∞, −10]$

Ejemplo$\PageIndex{4}$

Resolver:

$−7(2x+1)<1$.

Solución:

$\begin{aligned} -7(2x+1)&<1 & & \color{Cerulean}{Distribute.} \\ -14x-7&<1 \\ -14x-7\color{Cerulean}{+7}&<1\color{Cerulean}{+7} \\ 14x&<8 \\ \frac{-14x}{\color{Cerulean}{-14}}&\color{OliveGreen}{>}\color{black}{\frac{8}{\color{Cerulean}{-14}}} & & \color{Cerulean}{Reverse\:the\:inequality.} \\ x&>-\color{black}{\frac{8\color{Cerulean}{\div 2}}{14\color{Cerulean}{\div 2}}} & & \color{Cerulean}{Reduce.} \\ x&>-\frac{4}{7} \end{aligned}$

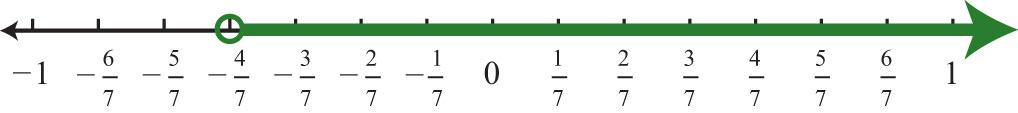
$Captura de pantalla (851) .png$

Figura$\PageIndex{3}$

Respuesta:

Notación de intervalos:$(−\frac{4}{7}, ∞)$

Ejemplo$\PageIndex{5}$

Resolver:

$5x−3(2x−1)≥2(x−3)$.

Solución:

$Captura de pantalla (852) .png$

Figura$\PageIndex{4}$

Respuesta:

Notación de intervalos:$(−∞, 3]$

Ejercicio$\PageIndex{1}$

Resolver:

$3−5(x−1)≤28$.

Contestar: $[−4, ∞)$

Desigualdades compuestas

A continuación se presentan algunos ejemplos de desigualdades lineales compuestas:

$-3<2x+5<17$

$-1\leq\frac{1}{2}x-3<1$

$3x+1<10\quad or\quad 2x-1\geq 11$

Estas desigualdades compuestas son en realidad dos desigualdades en una sola declaración unidas por la palabra “y” o por la palabra “o”. Por ejemplo,

$-3<2x+5<17$

es una desigualdad compuesta porque se puede descomponer de la siguiente manera:

$-3<2x+5\quad\text{and}\quad 2x+5<17$

Resuelve cada desigualdad individualmente, y la intersección de los dos conjuntos de soluciones resuelve la desigualdad compuesta original. Si bien este método funciona, hay otro método que suele requerir menos pasos. Aplicar las propiedades de esta sección a las tres partes de la desigualdad compuesta con el objetivo de aislar la variable en medio de la declaración para determinar los límites del conjunto de soluciones.

Ejemplo$\PageIndex{6}$

Resolver:

$−3<2x+5<17$.

Solución:

$\begin{array}{c} {-3<2x+5<17}\\{-3\color{Cerulean}{-5}\color{black}{<2x+5}\color{Cerulean}{-5}\color{black}{<17}\color{Cerulean}{-5}}\\{-8<2x<12}\\{\frac{-8}{\color{Cerulean}{2}}\color{black}{<\frac{2x}{\color{Cerulean}{2}}<\frac{12}{\color{Cerulean}{2}}}}\\{-4<x<6} \end{array}$

$Captura de pantalla (853) .png$

Figura$\PageIndex{5}$

Respuesta:

Notación de intervalos:$(−4, 6)$

Ejemplo$\PageIndex{7}$

Resolver:

$−1≤\frac{1}{2}x−3<1$.

Solución:

$\begin{array}{c}{-1\leq\frac{1}{2}x-3<1}\\{-1\color{Cerulean}{+3}\color{black}{\leq\frac{1}{2}x-3}\color{Cerulean}{+3}\color{black}{<1}\color{Cerulean}{+3}}\\{2\leq\frac{1}{2}x<4}\\{\color{Cerulean}{2}\color{black}{\cdot 2\leq}\color{Cerulean}{2}\color{black}{\cdot\frac{1}{2}x<}\color{Cerulean}{2}\color{black}{\cdot 4}}\\{4\leq x<8} \end{array}$

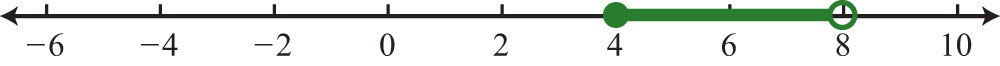
$Captura de pantalla (855) .png$

Figura$\PageIndex{6}$

Respuesta:

Notación de intervalos:$[4, 8)$

Es importante señalar que al multiplicar o dividir las tres partes de una desigualdad compuesta por un número negativo, se deben revertir todas las desigualdades en el enunciado. Por ejemplo,

$\begin{array}{c}{-10<-2x<20}\\{\frac{-10}{\color{Cerulean}{-2}}\color{OliveGreen}{>}\color{black}{\frac{-2x}{\color{Cerulean}{-2}}}\color{OliveGreen}{>}\color{black}{\frac{20}{\color{Cerulean}{-2}}}}\\{5>x>-10} \end{array}$

La respuesta anterior se puede escribir en una forma equivalente, donde los números más pequeños se encuentran a la izquierda y los números más grandes se encuentran a la derecha, ya que aparecen en una recta numérica.

$-10<x<5$

Usando la notación de intervalos, escriba$(−10, 5)$.

Ejercicio$\PageIndex{2}$

Resolver:

$−8≤2(−3x+5)<34$.

Contestar: $(−4, 3]$

Para las desigualdades compuestas con la palabra “o” se deben trabajar ambas desigualdades por separado y luego considerar la unión de los conjuntos de soluciones. Los valores en esta unión resuelven cualquiera de las dos desigualdades.

Ejemplo$\PageIndex{8}$

Resolver:

$3x+1<10$o$2x−1≥11$.

Solución:

Resuelve cada desigualdad y forma la unión combinando los conjuntos de soluciones.

$\begin{array}{ccc}{3x+1<10}&{}&{2x-1\geq 11}\\{3x+1\color{Cerulean}{-1}\color{black}{<10}\color{Cerulean}{-1}}&{}&{2x-1\color{Cerulean}{+1}\color{black}{\geq 11}\color{Cerulean}{+1}}\\{3x<9}&{\text{or}}&{2x\geq 12}\\{\frac{3x}{\color{Cerulean}{3}}\color{black}{<\frac{9}{\color{Cerulean}{3}}}}&{}&{\frac{2x}{\color{Cerulean}{2}}\color{black}{\geq \frac{12}{\color{Cerulean}{2}}}}\\{x<3}&{}&{x\geq 6} \end{array}$

$Captura de pantalla (856) .png$

Figura$\PageIndex{7}$

Respuesta:

Notación de intervalos:$(−∞, 3)∪[6, ∞)$

Ejercicio$\PageIndex{3}$

Resolver:

$4x−1<-5$o$4x-1>5$.

Contestar: $(−∞,−1)∪(\frac{3}{2}, ∞)$

Aplicaciones de Desigualdades Lineales

A continuación se resumen algunas de las palabras y frases clave que indican desigualdades:

Mesa$\PageIndex{1}$
Frases Clave	Traducción
Un número es al menos$5$.	$x\geq 5$
Un número es$5$ o más inclusivo.	$x\geq 5$
Un número es como mucho$3$.	$x\leq 3$
Un número es$3$ o menos inclusivo.	$x\leq 3$
Un número es estrictamente menor que$4$.	$x<4$
Un número es menor que$4$, no inclusivo.	$x<4$
Un número es mayor que$7$.	$x>7$
Un número es más que$7$, no inclusivo.	$x>7$
Un número está en el medio$2$ y$10$.	$2<x<10$
Un número es al menos$5$ y como máximo$15$.	$5\leq x\leq 15$
Un número puede variar de$5$ a$15$.	$5\leq x\leq 15$

Al igual que con todas las aplicaciones, lee atentamente el problema varias veces y busca palabras y frases clave. Identificar las incógnitas y asignar variables. A continuación, traducir la redacción en una desigualdad matemática. Por último, usa las propiedades que has aprendido para resolver la desigualdad y expresar la solución gráficamente o en notación de intervalos.

Ejemplo$\PageIndex{9}$

Traducir:

Cinco menos del doble de un número es como máximo$25$.

Solución:

Primero, elija una variable para el número desconocido e identifique las palabras y frases clave.

$\begin{array}{cccc}{\color{Cerulean}{twice\:a\:number}}&{\color{Cerulean}{five\:less\:than}}&{\color{Cerulean}{is\:at\:most}}&{}\\{\overbrace{\:\:2n\:\:}}&{\overbrace{\:\:-\:\:5\:\:}}&{\overbrace{\:\:\leq\:\:}}&{25} \end{array}$

Respuesta:

$2n−5≤25$.

La frase clave “es como máximo” indica que la cantidad tiene un valor máximo de$25$ o menor.

Ejemplo$\PageIndex{10}$

La temperatura en el desierto puede variar de$10°C$ a$45°C$ en un periodo$24$ de una hora. Encuentra el rango equivalente en grados Fahrenheit,$F$, dado eso$C=\frac{5}{9}(F−32)$.

Solución:

Establecer una desigualdad compuesta donde la temperatura en Celsius esté inclusivamente entre$10°C$ y$45°C$. Después sustituir la expresión equivalente a la temperatura Celsius en la desigualdad y resolver para$F$.

$\begin{array}{c}{10°C\leq\color{OliveGreen}{temperature\:in\:Celsius}\color{black}{\leq 45°C}}\\{10\leq\color{OliveGreen}{\frac{5}{9}(F-32)}\color{black}{\leq 45}}\\{\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{10\leq}\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{\frac{5}{9}(F-32)\leq}\color{Cerulean}{\frac{9}{5}\cdot}\color{black}{45}}\\{18\leq F-32\leq 81}\\{18\color{Cerulean}{+32}\color{black}{\leq F-32}\color{Cerulean}{+32}\color{black}{\leq 81}\color{Cerulean}{+32}}\\{50\leq F\leq 113}\end{array}$

Respuesta:

El rango equivalente de Fahrenheit es de$50°F$ a$113°F$.

Ejemplo$\PageIndex{11}$

En los primeros cuatro eventos de un encuentro, una gimnasta anota$7.5, 8.2, 8.5$, y$9.0$. ¿Qué debe anotar en el quinto evento para promediar al menos$8.5$?

Solución:

El promedio debe ser al menos$8.5$; esto quiere decir que el promedio debe ser mayor o igual a$8.5$.

$\begin{aligned} average &\geq 5 \\ \frac{7.5+8.2+8.5+9.0+x}{5}&\geq 8.5 \\ \frac{33.2+x}{5}&\geq 8.5 \\ \color{Cerulean}{5\cdot}\color{black}{\frac{33.2+x}{5}}&\geq\color{Cerulean}{5\cdot}\color{black}{8.5} & & \color{Cerulean}{Multiply\:both\:sides\:by\:5.} \\ 33.2+x&\geq 42.5 \\ 33.2+x\color{Cerulean}{-33.2}&\geq 42.5\color{Cerulean}{-33.2} \\ x&\geq 9.3 \end{aligned}$

Respuesta:

Debe anotar al menos$9.3$ en el quinto evento.

Claves para llevar

Las desigualdades suelen tener infinitamente muchas soluciones. Las soluciones se presentan gráficamente en una recta numérica o usando notación de intervalo o ambas.
Todas menos una de las reglas para resolver las desigualdades lineales son las mismas que para resolver ecuaciones lineales. Si divide o multiplica una desigualdad por un número negativo, invierta la desigualdad para obtener una desigualdad equivalente.
Las desigualdades compuestas que involucran la palabra “o” requieren que resolvamos cada desigualdad y formemos la unión de cada conjunto de soluciones. Estos son los valores que resuelven al menos una de las desigualdades dadas.
Las desigualdades compuestas que involucran la palabra “y” requieren la intersección de los conjuntos de soluciones para cada desigualdad. Estos son los valores que resuelven ambas o todas las desigualdades dadas.
Los lineamientos generales para resolver problemas verbales se aplican a las aplicaciones que involucran desigualdades. Tenga en cuenta una nueva lista de palabras y frases clave que indican una configuración matemática que involucra desigualdades.

Ejercicio$\PageIndex{4}$ Checking for Solutions

Determinar si el número dado es una solución a la desigualdad dada.

$2x−3<6; x=-1$
$-3x+1\leq 0; x=-2$
$5x-20>0; x=3$
$\frac{1}{2}x+1>−\frac{3}{4}; x=−\frac{1}{4}$
$−5<7x+1<9; x=0$
$−20≤−3x−5≤−10; x=5$
$x<-3 \text{ or }x>3; x=−10$
$x<0\text{ or }x≥1; x=\frac{1}{2}$
$2x+1<−3\text{ or }2x+1≥5; x=2$
$4x−1<−17\text{ or }3x+2≥6; x=1$

Contestar

1. Sí

3. No

5. Sí

7. Sí

9. Sí

Ejercicio$\PageIndex{5}$ Solving Linear Inequalities

Resuelve y grafica el conjunto de soluciones. Además, presentar la solución establecida en notación de intervalos.

$x+5>1$
$x−3<−4$
$6x≤24$
$4x>−8$
$−7x≤14$
$−2x+5>9$
$7x−3≤25$
$12x+7>−53$
$−2x+5<-7$
$-2x+4\leq 4$
$-15x+10>20$
$−8x+1≤29$
$\frac{1}{7}x−3<1$
$\frac{1}{2}x−\frac{1}{3}>\frac{2}{3}$
$\frac{5}{3}x+\frac{1}{2}≤\frac{1}{3}$
$−\frac{3}{4}x−\frac{1}{2}≥\frac{5}{2}$
$−\frac{1}{5}x+\frac{3}{4}<−\frac{1}{5}$
$−\frac{2}{3}x+1<-3$
$2(-3x+1)<14$
$-7(x-2)+1<15$
$9x-3(3x+4)>−12$
$12x−4(3x+5)≤−2$
$5−3(2x−6)≥−1$
$9x−(10x−12)<22$
$2(x-7)-3(x+3)\leq -3$
$5x-3>3x+7$
$4(3x−2)≤−2(x+3)+12$
$5(x−3)≥15x−(10x+4)$
$12x+1>2(6x−3)−5$
$3(x−2)+5>2(3x+5)+2$
$−4(3x−1)+2x≤2(4x−1)−3$
$−2(x−2)+14x<7(2x+1) $

Contestar

1. $x>−4; (−4, ∞)$

$Captura de pantalla (859) .png$

Figura$\PageIndex{8}$

3. $x≤4; (−∞, 4]$

$Captura de pantalla (861) .png$

Figura$\PageIndex{9}$

5. $x≥−2; [−2, ∞)$

$Captura de pantalla (865) .png$

Figura$\PageIndex{10}$

7. $x≤4; (−∞, 4]$

$Captura de pantalla (867) .png$

Figura$\PageIndex{11}$

9. $x>6; (6, ∞)$

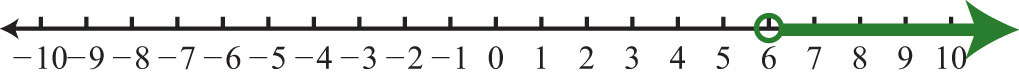
$Captura de pantalla (870) .png$

Figura$\PageIndex{12}$

11. $x<−\frac{2}{3}; (−∞, −\frac{2}{3})$

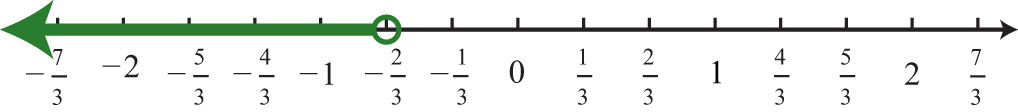
$Captura de pantalla (872) .png$

Figura$\PageIndex{13}$

13. $x<28; (−∞, 28)$

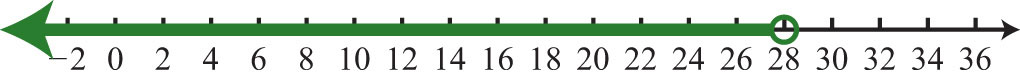
$Captura de pantalla (876) .png$

Figura$\PageIndex{14}$

15. $x≤−\frac{1}{10}; (−∞, −\frac{1}{10}]$

$Captura de pantalla (878) .png$

Figura$\PageIndex{15}$

17. $x>\frac{19}{4}; (\frac{19}{4}, ∞)$

$Captura de pantalla (880) .png$

Figura$\PageIndex{16}$

19. $x>−2; (−2, ∞)$

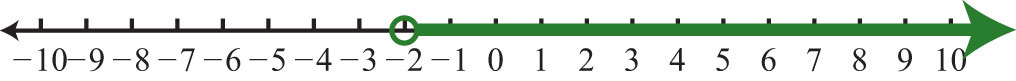
$Captura de pantalla (882) .png$

Figura$\PageIndex{17}$

21. $∅$

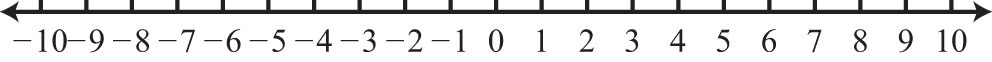
$Captura de pantalla (884) .png$

Figura$\PageIndex{18}$

23. $x≤4; (−∞, 4]$

$Captura de pantalla (886) .png$

Figura$\PageIndex{19}$

25. $x≥−20; [−20, ∞)$

$Captura de pantalla (888) .png$

Figura$\PageIndex{20}$

27. $x≤1; (−∞, 1]$

$Captura de pantalla (890) .png$

Figura$\PageIndex{21}$

29. $R$

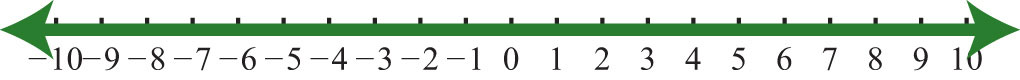
$Captura de pantalla (892) .png$

Figura$\PageIndex{22}$

31. $x≥\frac{1}{2}; [\frac{1}{2}, ∞)$

$Captura de pantalla (894) .png$

Figura$\PageIndex{23}$

Ejercicio$\PageIndex{6}$ Solving Linear Inequalities

Establecer una desigualdad algebraica y luego resolverla.

La suma de tres veces un número y$4$ es mayor que negativa$8$.
La suma de$7$ y tres veces un número es menor o igual a$1$.
Cuando se resta un número$10$, el resultado es como mucho$12$.
Cuando se resta un número de$5$ veces$6$, el resultado es al menos$26$.
Si se agrega cinco a tres veces un número, entonces el resultado es menor a veinte.
Si se resta tres de dos veces un número, entonces el resultado es mayor o igual a nueve.
Bill gana $$12.00$ por el día más $$0.25$ por cada persona que consigue registrarse para votar. ¿Cuántas personas debe registrarse para ganar al menos $$50.00$ por el día?
Con una membresía de club de golf que cuesta $$100$ por mes, cada ronda de golf cuesta solo $$25.00$. ¿Cuántas rondas de golf puede jugar un miembro si desea mantener sus costos a $$250$ mensuales como máximo?
Joe obtuvo puntajes de$72, 85$, y$75$ en sus primeros tres exámenes de álgebra. ¿Qué debe puntuar en el cuarto examen para promediar al menos$80$?
Maurice ganó$4, 7$, y$9$ señala$10$ en los tres primeros cuestionarios. ¿Qué debe puntuar en el cuarto cuestionario para promediar al menos$7$?
Una computadora está configurada para apagarse si la temperatura excede$40°C$. Dar una declaración equivalente usando grados Fahrenheit. (Pista:$C=\frac{5}{9}(F−32)$.)
Se garantiza que cierta marca de maquillaje no se ejecutará si la temperatura es inferior a$35°C$. Dar una declaración equivalente usando grados Fahrenheit.

Contestar

1. $n>−4$

3. $n≥−2$

5. $n<5$

7. Bill debe registrar al menos$152$ personas.

9. Joe debe ganar al menos un$88$ en el cuarto examen.

11. La computadora se apagará cuando la temperatura supere los$104$ °F.

Ejercicio$\PageIndex{7}$ Compound Inequalities

Resuelve y grafica el conjunto de soluciones. Además, presentar la solución establecida en notación de intervalos.

$−1<x+3<5$
$−10≤5x<20$
$−2≤4x+6<10$
$−10≤3x−1≤−4$
$−15<3x−6≤6$
$−22<5x+3≤3$
$−1≤\frac{1}{2}x−5≤1$
$1<8x+5<5$
$−\frac{1}{5}≤\frac{2}{3}x−\frac{1}{5}<\frac{4}{5}$
$−\frac{1}{2}<\frac{3}{4}x−\frac{2}{3}≤\frac{1}{2}$
$−3≤3(x−1)≤3$
$−12<6(x−3)≤0$
$4<−2(x+3)<6$
$−5≤5(−x+1)<15$
$−\frac{3}{2}≤\frac{1}{4}(\frac{1}{2}x−1)+\frac{3}{4}<\frac{3}{2}$
$−4≤−\frac{1}{3}(3x+12)<4$
$−2≤12−2(x−3)≤20$
$−5<2(x-1)-3(x+2)<5$
$3x\leq -15\text{ or }2x>6$
$4x−1<-17\text{ or }3x+2\geq 8$
$-2x+1<-1\text{ or }-2x+1>1$
$7x+4≤4\text{ or }6x−5≥1$
$3x−7<14\text{ or }2x+3>7$
$−3x+1<-5\text{ or }-4x-3>−23$
$\frac{1}{2}x−2<-1\text{ or }\frac{1}{2}x-2>1$
$\frac{1}{3}x+3≥−2\text{ or }\frac{1}{3}x+3≤2$
$3x+7≤7\text{ or }−5x+6>6$
$−10x−3≤17\text{ or }20x−6>−26$
$2x−10<-2\text{ or }-3x+4>−5$
$5x+3<4\text{ or }5-10x>4$
$3x<18\text{ and }5x>-20$
$x+7\leq 5\text{ and } x−3≥−10$
$2x−1<5\text{ and }3x-1<10$
$5x+2<-13\text{ and }3x+4>13$

Contestar

1. $−4<x<2; (-4,2)$

$Captura de pantalla (896) .png$

Figura$\PageIndex{24}$

3. $−2≤x<1; [−2, 1)$

$Captura de pantalla (898) .png$

Figura$\PageIndex{25}$

5. $-3<x\leq 4; (-3,4]$

$Captura de pantalla (900) .png$

Figura$\PageIndex{26}$

7. $8≤x≤12; [8, 12]$

$Captura de pantalla (902) .png$

Figura$\PageIndex{27}$

9. $0≤x<\frac{3}{2}; [0, \frac{3}{2})$

$Captura de pantalla (904) .png$

Figura$\PageIndex{28}$

11. $0≤x≤2; [0, 2]$

$Captura de pantalla (906) .png$

Figura$\PageIndex{29}$

13. $-6<x<-5; (-6,-5)$

$Captura de pantalla (908) .png$

Figura$\PageIndex{30}$

15. $−16≤x<8; [−16, 8)$

$Captura de pantalla (910) .png$

Figura$\PageIndex{31}$

17. $−1≤x≤10; [−1, 10]$

$Captura de pantalla (912) .png$

Figura$\PageIndex{32}$

19. $x≤−5\text{ or }x>3; (−∞, −5]∪(3, ∞)$

$Captura de pantalla (914) .png$

Figura$\PageIndex{33}$

21. $x>1\text{ or }x<0; (−∞, 0)∪(1, ∞)$

$Captura de pantalla (916) .png$

Figura$\PageIndex{34}$

23. $R$

$Captura de pantalla (892) .png$

Figura$\PageIndex{35}$

25. $x<2\text{ or }x>6; (−∞, 2)∪(6, ∞) $

$Captura de pantalla (918) .png$

Figura$\PageIndex{36}$

27. $x≤0; (−∞, 0]$

$Captura de pantalla (920) .png$

Figura$\PageIndex{37}$

29. $x<4; (−∞, 4)$

$Captura de pantalla (922) .png$

Figura$\PageIndex{38}$

31. $-4<x<6; (-4,6)$

$Captura de pantalla (924) .png$

Figura$\PageIndex{39}$

33. $x<3; (−∞, 3)$

$Captura de pantalla (926) .png$

Figura$\PageIndex{40}$

Ejercicio$\PageIndex{8}$ Compound Inequalities

Establecer una desigualdad compuesta para lo siguiente y luego resolver.

Cinco más de dos veces algún número está entre$15$ y$25$.
Cuatro restado de tres veces algún número es entre$−4$ y$14$.
Clint desea ganar una B, que es al menos$80$ pero menor que$90$. ¿Qué rango debe puntuar en el cuarto examen si los tres primeros fueron$65, 75$, y$90$?
Un cierto anticongelante es efectivo para un rango de temperatura de$−35°C$ a$120°C$. Encuentra el rango equivalente en grados Fahrenheit.
La temperatura promedio en Londres va desde$23°C$ en verano hasta$14°C$ en invierno. Encuentra el rango equivalente en grados Fahrenheit.
Si la base de un triángulo mide$5$ pulgadas, entonces ¿en qué rango debe estar la altura para que el área esté entre pulgadas$10$ cuadradas y pulgadas$20$ cuadradas?
Un rectángulo tiene una longitud de$7$ pulgadas. Encuentre todos los anchos posibles si el área debe ser de al menos pulgadas$14$ cuadradas y como máximo pulgadas$28$ cuadradas.
Un rectángulo tiene un ancho de$3$ centímetros. Encuentra todas las longitudes posibles, si el perímetro debe ser de al menos$12$ centímetros y como máximo$26$ centímetros.
El perímetro de un cuadrado debe estar entre$40$ pies y$200$ pies. Encuentra la longitud de todos los lados posibles que satisfagan esta condición.
Si dos veces un ángulo es entre$180$ grados y$270$ grados, entonces ¿cuáles son los límites del ángulo original?
Si tres veces un ángulo es entre$270$ grados y$360$ grados entonces ¿cuáles son los límites del ángulo original?

Contestar

1. $5<n<20$

3. Clint debe obtener una puntuación en el rango de$90$ a$100$.

5. La temperatura promedio en Londres varía de$57.2°F$ a$73.4°F$.

7. El ancho debe ser de al menos$2$ pulgadas y como máximo$4$ pulgadas.

9. Los lados deben estar entre$10$ los pies y$50$ los pies.

11. El ángulo es entre$90$ grados y$120$ grados.

Ejercicio$\PageIndex{9}$ Discussion Board Topics

Investigar y discutir el uso de la notación set-builder con intersecciones y uniones.
¿Podemos combinar “o” lógico en una sola declaración como lo hacemos para “y” lógica?

Contestar: 2. Las respuestas pueden variar

Frases Clave	Traducción
Un número es al menos\(5\).	\(x\geq 5\)
Un número es\(5\) o más inclusivo.	\(x\geq 5\)
Un número es como mucho\(3\).	\(x\leq 3\)
Un número es\(3\) o menos inclusivo.	\(x\leq 3\)
Un número es estrictamente menor que\(4\).	\(x<4\)
Un número es menor que\(4\), no inclusivo.	\(x<4\)
Un número es mayor que\(7\).	\(x>7\)
Un número es más que\(7\), no inclusivo.	\(x>7\)
Un número está en el medio\(2\) y\(10\).	\(2<x<10\)
Un número es al menos\(5\) y como máximo\(15\).	\(5\leq x\leq 15\)
Un número puede variar de\(5\) a\(15\).	\(5\leq x\leq 15\)

Search

Text Color

Text Size

Margin Size

Font Type

Desigualdades compuestas

Aplicaciones de Desigualdades Lineales

Claves para llevar