2.6: Aplicaciones de proporción y proporción

Última actualización
Guardar como PDF

Page ID: 110136

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Entender la diferencia entre una proporción y una proporción.
Resolver proporciones usando multiplicación cruzada.
Resuelve aplicaciones que involucran proporciones, incluyendo triángulos similares.

Definiciones

Una relación es una relación entre dos números o cantidades generalmente expresadas como cociente. Las relaciones se expresan típicamente usando la siguiente notación:

$\frac{a}{b}\qquad a\:to\:b\qquad a:b$

Todo lo anterior son formas equivalentes que se utilizan para expresar una proporción. Sin embargo, la forma más familiar de expresar una proporción es en forma de fracción. Al escribir ratios, es importante prestar atención a las unidades. Si las unidades son las mismas, entonces la relación se puede escribir sin ellas.

Ejemplo$\PageIndex{1}$

Exprese la relación$12$ pies a$48$ pies en forma reducida.

Solución:

$\begin{aligned} 12\text{ feet to }48\text{ feet} &=\frac{12\text{ feet}}{48\text{ feet}} \\ &=\color{black}{\frac{12\color{Cerulean}{\div 12}}{48\color{Cerulean}{\div 12}}} &\color{Cerulean}{Reduce.} \\ &=\frac{1}{4} \end{aligned}$

Respuesta:

$1$a$4$

Si las unidades son diferentes, entonces debemos asegurarnos de incluirlas porque la relación representa una tasa.

Ejemplo$\PageIndex{2}$

Exprese la relación$220$ millas a$4$ horas en forma reducida.

Solución:

$\begin{aligned} 220\text{ miles to }4\text{ hours}&=\frac{220\text{ miles}}{4\text{ hours}} \\ &=\frac{55\text{miles}}{1\text{ hour}} \\ &=55\text{ miles\hour} \end{aligned}$

Respuesta:

$55$millas a$1$ horas (o$55$ millas por hora)

Las tarifas son útiles a la hora de determinar el costo unitario, o el precio de cada unidad. Utilizamos el costo unitario para comparar valores cuando las cantidades no son las mismas. Para determinar el costo unitario, divida el costo por el número de unidades.

Ejemplo$\PageIndex{3}$

Un supermercado local ofrece un paquete de$12$ refrescos por $ a$3.48$ la venta, y el almacén local de descuentos ofrece el refresco en una caja$36$ de lata por $$11.52$. ¿Cuál es el mejor valor?

Solución:

Divide el costo por el número de latas para obtener el precio unitario.

Mesa$\PageIndex{1}$
Supermercado	Almacén de descuento
$$3.4812$ latas$=$ $$0.29$ /lata	$$11.5236$ latas$=$ $$0.32$ /lata

Respuesta:

El precio de venta de supermercado de $$3.48$ por un$12$ -pack es una mejor relación calidad-precio en $$0.29$ por lata.

Una proporción es una declaración de igualdad de dos proporciones.

\[\frac{a}{b}=\frac{c}{d}\]

Esta proporción a menudo se lee “$a$es$b$ como$c$ es a”$d$. He aquí un ejemplo de una proporción simple,

$\frac{1}{2}=\frac{2}{4}$

Si limpiamos las fracciones multiplicando ambos lados de la proporción por el producto de los denominadores$8$, entonces obtenemos la siguiente afirmación verdadera:

$\begin{aligned}\color{Cerulean}{8\cdot}\color{black}{\frac{1}{2}}&=\color{Cerulean}{8\cdot}\color{black}{\frac{2}{4}} \\ 4\cdot 1&=2\cdot 2\\ 4&=4 \end{aligned}$

Dados los números reales distintos de cero$a, b, c,$ y$d$ que satisfagan una proporción, multiplique ambas caras por el producto de los denominadores para obtener lo siguiente:

$\begin{aligned} \frac{a}{b}&=\frac{c}{d} \\ \color{Cerulean}{bd}\color{black}{\cdot \frac{a}{b}}&=\color{Cerulean}{bd}\color{black}{\cdot \frac{c}{d}} \\ ad&=bc \end{aligned}$

Esto muestra que los productos cruzados son iguales, y comúnmente se conoce como multiplicación cruzada.

\[\text{If }\frac{a}{b}=\frac{c}{d}\text{ then }ad=bc\]

Resolviendo Proporciones

Multiplicar cruz para resolver proporciones donde se desconocen términos.

Ejemplo$\PageIndex{4}$

Resolver:

$\frac{5}{8}=\frac{n}{4}$.

Solución:

Cruzar multiplicar y luego resolver para$n$.

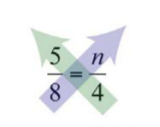$Captura de pantalla (765) .png$

Figura$\PageIndex{1}$

$\begin{aligned} 5\cdot 4&=8\cdot n &\color{Cerulean}{Cross\:multiply.} \\ 20&=8n \\ \frac{20}{\color{Cerulean}{8}} &=\frac{8n}{\color{Cerulean}{8}} &\color{Cerulean}{Divide\:by\:8.} \\ \color{black}{\frac{20\color{Cerulean}{\div 4}}{8\color{Cerulean}{\div 4}}} &=n &\color{Cerulean}{Reduce.} \\ \frac{5}{2}&=n \end{aligned}$

Respuesta:

$n=\frac{5}{2}$

Ejemplo$\PageIndex{5}$

Resolver:

$\frac{15}{x}=\frac{5}{6}$.

Solución:

Cruzar multiplicar luego resolver para$x$.

$\begin{aligned} \frac{15}{x}&=\frac{5}{6} \\ 15\cdot 6&=x\cdot 5 \\ 15\cdot 6&=5x \\ \frac{15\cdot 6}{\color{Cerulean}{5}}&=\frac{5x}{\color{Cerulean}{5}} \\ 3\cdot 6&=1x \\ 18&=x \end{aligned}$

Respuesta:

$x=18$

Ejemplo$\PageIndex{6}$

Resolver:

$\frac{n+3}{5}=\frac{7}{2}$.

Solución:

Al multiplicar en cruz, asegúrese de agrupar$n+3$. Aplicar la propiedad distributiva en el siguiente paso.

$\begin{aligned} \frac{n+3}{5}&=\frac{7}{2} &\color{Cerulean}{Cross\:multiply.} \\ (n+3)\cdot 2&=5\cdot 7 &\color{Cerulean}{Distribute.} \\ 2n+6&=35 &\color{Cerulean}{Solve.} \\ 2n+6\color{Cerulean}{-6}&=35\color{Cerulean}{-6} \\ 2n&=29 \\ \frac{2n}{\color{Cerulean}{2}}&=\frac{29}{\color{Cerulean}{2}} \\ n&=\frac{29}{2} \end{aligned}$

Respuesta:

$n=\frac{29}{2}$

Ejercicio$\PageIndex{1}$

Resolver:

$\frac{5}{3}=\frac{3n−1}{2}$.

Contestar: $n=\frac{13}{9}$

Aplicaciones

Al establecer proporciones, la consistencia con las unidades de cada ratio es crítica. Las unidades para los numeradores deben ser las mismas y las unidades para los denominadores también deben ser las mismas.

Ejemplo$\PageIndex{7}$

Se afirma que$2$ fuera de los$3$ dentistas prefieren cierta marca de pasta de dientes. Si se encuestan a 600 odontólogos, entonces ¿cuántos dirán que prefieren esa marca?

Solución:

Primero, identificar lo desconocido y asignarle una variable.

Dejar$n$ representar el número de dentistas encuestados que prefieren el nombre de la marca.

Ya que estás buscando el número de dentistas que prefieren la marca de un total de$600$ encuestados, construye las proporciones con el número de dentistas que prefieren la marca en el numerador y el número total encuestado en el denominador.

$\begin{aligned} \underline{2}=\underline{n} &\quad\color{Cerulean}{\leftarrow\:number\:of\:dentists\:who\:prefer\:the\:brand} \\ 3\:\:600&\quad\color{Cerulean}{\leftarrow\:total\:number\:of\:dentists\:surveyed} \end{aligned}$

Cruzar multiplicar y resolver para$n$,

$\begin{aligned} 2\cdot 600&=3\cdot n \\ \frac{2\cdot 600}{\color{Cerulean}{3}}&=\frac{3\cdot n}{\color{Cerulean}{3}} \\ 2\cdot 200&=1n \\ 400&=n \end{aligned}$

Respuesta:

La afirmación sugiere que de$400$ los$600$ dentistas encuestados prefieren el nombre de la marca.

Ejemplo$\PageIndex{8}$

En el condado de Tulare,$3$ de todos los$7$ votantes dijeron que sí a la Proposición 40. Si la$42,000$ gente votaba, ¿cuántos decían no a la Proposición 40?

Solución:

El problema da la proporción de votantes que dijeron que sí, pero pide el número que dijo que no.

Que$n$ represente el número de electores que dijeron que no.

Si$3$ fuera de$7$ dicho sí, entonces podemos asumir$4$ por$7$ dicho no. Establecer las proporciones con el número de electores que dijeron no en el numerador y el número total de votantes en el denominador.

$\begin{aligned} &\underline{4}=\:\:\:\:\underline{n}&\color{Cerulean}{\leftarrow\:voters\:who\:voted\:no} \\ &7\:\:\:\:\:\:42,000&\color{Cerulean}{\leftarrow\:total\:number\:of\:voters} \end{aligned}$

Cruzar multiplicar y resolver para$n$.

$\begin{aligned} 4\cdot 42,000&=7\cdot n \\ \frac{4\cdot 42,000}{\color{Cerulean}{7}}&=\frac{7\cdot n}{\color{Cerulean}{7}} \\ 24,000&=n \end{aligned}$

Respuesta:

$24,000$votantes de$42,000$ dicho no.

Ejemplo$\PageIndex{9}$

La suma de dos enteros en la relación de$4$ a$5$ es$27$. Encuentra los enteros.

Solución:

La suma de dos enteros es$27$; usa esta relación para evitar dos variables.

Dejar$n$ representar uno de los enteros.

Let$27-n$ representar el otro entero.

Los números enteros se dan para estar en la proporción de$4$ a$5$. Establezca la siguiente proporción:

$\begin{aligned} \frac{4}{5}&=\frac{n}{27-n} \\ 4\cdot (27-n)&=5\cdot n \\ 108-4n&=5n \\ 108-4n\color{Cerulean}{+4n} &=5n\color{Cerulean}{+4n} \\ 108&=9n \\ \frac{108}{\color{Cerulean}{9}}&=\frac{9n}{\color{Cerulean}{9}} \\ 12&=n \end{aligned}$

Utilízalo$27 − n$ para determinar el otro entero.

$27-n=27-\color{OliveGreen}{12}\color{black}{=15}$

Respuesta:

Los enteros son$12$ y$15$.

Ejercicio$\PageIndex{2}$

Una receta requiere$5$ cucharadas de azúcar por cada$8$ taza de harina. ¿Cuántas cucharadas de azúcar se requieren para$32$ las tazas de harina?

Contestar: $20$cucharadas de azúcar

Triángulos similares

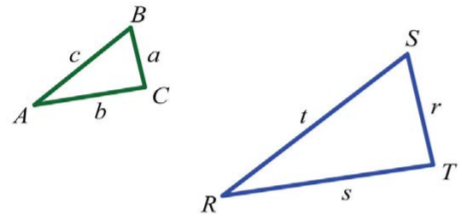
A menudo encontraremos problemas de proporción en geometría y trigonometría. Una aplicación involucra triángulos similares, que tienen la misma forma, pero no necesariamente del mismo tamaño. Las medidas de los ángulos correspondientes de triángulos similares son iguales, y las medidas de los lados correspondientes son proporcionales. Teniendo en cuenta triángulos similares$ABC$ y$RST$,

$Captura de pantalla (766) .png$

Figura$\PageIndex{2}$

Podemos escribir$ABC ~ RST$ y concluir que todos los ángulos correspondientes son iguales. La notación indica que ángulo$A$ corresponde al ángulo$R$ y que las medidas de estos ángulos son iguales:$A = R$.

$Captura de pantalla (767) .png$

Figura$\PageIndex{3}$

Además, las medidas de otros pares de ángulos correspondientes son iguales:$B = S$ y$C = T$.

$Captura de pantalla (768) .png$

Figura$\PageIndex{4}$

Use letras mayúsculas para los ángulos y una letra minúscula para denotar el lado opuesto al ángulo dado. Denote la proporcionalidad de las partes de la siguiente manera:

$\frac{a}{r}=\frac{b}{s}=\frac{c}{t}$

Ejemplo$\PageIndex{10}$

Si triángulo$ABC$ es similar a$RST$, donde$a=3, b=4, c=5,$ y$r=9$, luego encontrar los dos lados restantes.

Solución:

Dibuja una imagen e identifica las variables pictóricamente. Representar los lados desconocidos restantes por$s$ y$t$. Configura proporciones y resuelve los lados faltantes.

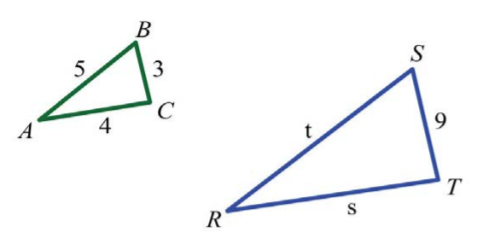$Captura de pantalla (769) .png$

Figura$\PageIndex{5}$

$\begin{array}{c|c}{\underline{Find\:t}}&{\underline{Find\:s}}\\{\begin{aligned} \frac{5}{t}&=\frac{3}{9} \\ 5\cdot 9&=t\cdot 3 \\ \frac{5\cdot 9}{\color{Cerulean}{3}}&=\frac{t\cdot 3}{\color{Cerulean}{3}} \\ 5\cdot 3&=t \\ 15&=t \end{aligned}}&{\begin{aligned} \frac{4}{s}&=\frac{3}{9} \\ 4\cdot 9&=s\cdot 3 \\ \frac{4\cdot 9}{\color{Cerulean}{3}}&=\frac{s\cdot 3}{\color{Cerulean}{3}} \\ 4\cdot 3&=s \\ 12&=s \end{aligned}} \end{array}$

Respuesta:

Los dos lados restantes miden$12$ unidades y$15$ unidades.

La relación reducida de dos lados correspondientes de triángulos similares se denomina factor de escala. En el ejemplo anterior, la relación de los dos lados dados$a$ y$r$ es

$\frac{3}{9}=\frac{1}{3}$

Por lo tanto,$ABC$ el triángulo es similar al triángulo$RST$ con un factor de escala de$\frac{1}{3}$. Esto significa que cada pata del triángulo$ABC$ es$\frac{1}{3}$ de la medida de las correspondientes patas del triángulo$RST$. También, otro dato interesante es que los perímetros de triángulos similares están en la misma proporción que sus lados y comparten el mismo factor de escala.

Ejemplo$\PageIndex{11}$

Si un triángulo$ABC$ tiene un perímetro de$12$ unidades y es similar a$RST$ con un factor de escala de$\frac{1}{3}$, entonces encuentra el perímetro de triángulo$RST$.

Solución:

Dejar$x$ representar el perímetro del triángulo$RST$.

El factor de escala$\frac{1}{3}$ implica que los perímetros están en proporción a esta relación. Establezca una proporción de la siguiente manera:

$\begin{aligned} &\underline{1}=\underline{12} &\color{Cerulean}{\leftarrow\:perimeter\:of\:ABC} \\ &3\:\:\:\:\:\:x &\color{Cerulean}{\leftarrow\:perimeter\:of\:RST} \end{aligned}$

Cruzar multiplicar y resolver para$x$.

$\begin{aligned} 1\cdot x&=3\cdot 12 \\ x&=36 \end{aligned}$

Respuesta:

El perímetro del triángulo$RST$ es$36$ unidades.

Claves para llevar

Resolver proporciones multiplicando ambos lados de la ecuación por el producto de los denominadores, o multiplicar cruzando.
Al establecer una proporción, es importante asegurar unidades consistentes en los numeradores y denominadores.
Los ángulos correspondientes de triángulos similares son iguales y sus lados correspondientes son proporcionales. La relación de dos lados correspondientes determina el factor de escala, que se puede utilizar para resolver muchas aplicaciones que involucran triángulos similares.

Ejercicio$\PageIndex{3}$ Ratios and Rates

Exprese cada proporción en forma reducida.

$100$pulgadas:$250$ pulgadas
$480$píxeles:$320$ píxeles
$96$pies:$72$ pies
$240$millas$4$ horas
$96$pies$3$ segundos
$6,000$revoluciones$4$ minutos
El precio promedio de las acciones de Google en 2008 y las ganancias por acción fueron $$465.66$ y $$14.89$, respectivamente. ¿Cuál fue la relación precio-ganancias promedio de Google en 2008? (Fuente: Wolfram Alpha)
El F-22 Raptor tiene dos motores que producen cada uno$35,000$ libras de empuje. Si el peso de despegue de este avión de combate es de$50,000$ libras, calcule la relación propulsor/peso del avión. (Fuente: USAF)
Un almacén de descuento ofrece una caja de porciones$55$ individuales de avena instantánea por $$11.10$. El supermercado ofrece cajas más pequeñas del mismo producto que contienen porciones$12$ individuales por $$3.60$. ¿Qué tienda ofrece la mejor relación calidad-precio?
Joe y Mary desean hacer un viaje por carretera juntos y necesitan decidir a quién van a tomar el auto. Joe calculó que su auto es capaz de viajar$210$ millas en$12$ galones de gasolina. Mary calcula que su auto viaja$300$ millas en$19$ galones. ¿Cuál de sus autos obtiene más millas al galón?

Contestar

1. $2:5$

3. $4:3$

5. $32$pies por segundo

7. $31.27$

9. El almacén de descuento

Ejercicio$\PageIndex{4}$ Solving Proportions

Resolver.

$\frac{2}{3}=\frac{n}{150}$
$\frac{7}{n}=\frac{2}{15}$
$\frac{1}{3}=\frac{5}{n}$
$\frac{1}{25}=\frac{6}{n}$
$\frac{n}{8}=−\frac{3}{2}$
$\frac{n}{3}=−\frac{5}{7}$
$8=\frac{2n}{3}$
$\frac{5}{n}=−30$
$1=\frac{1}{n−1}$
$−1=−\frac{1}{n+1}$
$−\frac{40}{n}=−\frac{5}{3}$
$\frac{2n+1}{3}=−\frac{3}{5}$
$\frac{5}{3n+3}=\frac{2}{3}$
$\frac{n+1}{2n−1}=\frac{1}{3}$
$\frac{5n+7}{5}=\frac{n−1}{2}$
$−\frac{2}{n+3}=\frac{n+7}{6}$
Encuentra dos números en la proporción de$3$ a$5$ cuya suma es$160$. (Sugerencia: Utilice$n$ y$160 − n$ para representar los dos números.)
Encuentra dos números en la proporción de$2$ a$7$ cuya suma es$90$.
Encuentra dos números en la proporción de$−3$ a$7$ cuya suma es$80$.
Encuentra dos números en la proporción de$−1$ a$3$ cuya suma es$90$.
Un entero mayor es$5$ más que un número entero más pequeño. Si los dos enteros tienen una relación de$6$ para$5$ encontrar los enteros.
Un entero mayor es$7$ menor que dos veces un número entero más pequeño. Si los dos enteros tienen una relación de$2$ para$3$ encontrar los enteros.

Contestar

1. $n=100$

3. $n=15$

5. $n=−12$

7. $n=12$

9. $n=2$

11. $n=24$

13. $n=\frac{3}{2}$

15. $n=−\frac{19}{5}$

17. $60, 100$

19. $−60, 140$

21. $25, 30$

Ejercicio$\PageIndex{5}$ Solving Proportions

Dadas las siguientes proporciones, determinar cada relación,$x:y$.

$\frac{x}{3}=\frac{y}{4}$
$\frac{x−2y}{3}=−\frac{3y}{5}$
$\frac{2x+4y}{2x−4y}=\frac{3}{2}$
$\frac{x+y}{x−y}=\frac{3}{5}$

Contestar

1. $\frac{3}{4}$

3. $10$

Ejercicio$\PageIndex{6}$ Applications

Establezca una proporción y luego resuelva.

Si$4$ de cada uno de$5$ los votantes apoyan al gobernador, entonces ¿cuántas de las$1,200$ personas encuestadas apoyan al gobernador?
Si$1$ de cada uno de$3$ los votantes encuestados dijeron que votaron sí a la Proposición 23, entonces, ¿cuántas de las$600$ personas encuestadas votaron sí?
De los$460$ estudiantes encuestados, la proporción para apoyar el proyecto de remodelación del sindicato estudiantil fue$3$ a$5$. ¿Cuántos alumnos estaban a favor de la remodelación?
Un estimado$5$ de$7$ los estudiantes llevan deudas de tarjetas de crédito. Estimar el número de estudiantes que llevan deudas de tarjetas de crédito de un total de$14,000$ estudiantes.
Si la proporción de estudiantes de sexo femenino a masculino en la universidad es$6$ igual a$5$, entonces determinar el número de estudiantes varones del$11,000$ total de estudiantes.
En el año 2009 se estimó que habría$838$ muertes en Estados Unidos por cada$100,000$ pueblo. Si se estimó que la población total de Estados Unidos era de$307,212,123$ personas, entonces, ¿cuántas muertes se esperaban en Estados Unidos en 2009? (Fuente: CIA World Factbook)
En el año 2009 se estimó que habría$1,382$ nacimientos en Estados Unidos por cada$100,000$ pueblo. Si se estimó que la población total de Estados Unidos era de$307,212,123$ personas, entonces ¿cuántos nacimientos se esperaban en Estados Unidos en 2009? (Fuente: CIA World Factbook)
Si$2$ de cada uno de$7$ los votantes aprueban un aumento del impuesto a las ventas entonces determine el número de votantes de los$588$ encuestados que no apoyan el aumento.
Una receta requiere$1$ taza de jugo de limón para hacer$4$ tazas de limonada. ¿Cuánto jugo de limón se necesita para hacer$2$ galones de limonada?
El clásico cóctel “Shirley Temple” requiere$1$ parte de jarabe de cereza a$4$ partes de refresco de limón y lima. ¿Cuánto sirope de cereza se necesita para mezclar el cóctel dado una lata de$12$ -onza de refresco de limón y lima?
Una impresora imprime$30$ páginas en$1$ minutos. ¿Cuánto tiempo tardará en imprimir un folleto de$720$ -page?
Un mecanógrafo puede escribir$75$ palabras por minuto. ¿Cuánto tiempo tardará en escribir$72$ páginas si hay aproximadamente$300$ palabras por página?
En un mapa en particular, cada$\frac{1}{16}$ centímetro representa$1$ milla. ¿Cuántas millas representan las$3\frac{1}{2}$ pulgadas?
En una gráfica cada$1$ centímetro representa$100$ pies. ¿Qué medida en el mapa representa una milla?
Una tienda de golosinas ofrece dulces mixtos a $$3.75$ por cada media libra. ¿Cuánto costarán las$2.6$ libras de dulces?
Las nueces mixtas tienen un precio de $$6.45$ por libra. ¿Cuántas libras de nueces mixtas se pueden comprar con $$20.00$?
El maíz en el mercado de agricultores está empaquetado y tiene un precio de $$1.33$ para$6$ mazorcas. ¿Cuántas orejas se pueden comprar con $$15.00$?
Si$4$ las pizzas cuestan $$21.00$, entonces ¿cuánto costarán$16$ las pizzas?
Un cereal endulzado para el desayuno contiene$110$ calorías en una porción$\frac{3}{4}$ de taza. ¿Cuántas calorías hay en una porción$1\frac{7}{8}$ de taza?
El arroz con sabor a pollitos contiene$300$ calorías en cada porción de$2.5$ -onza. ¿Cuántas calorías hay en una$4$ cucharada de arroz con sabor a pollo?
Un hombre de$200$ -libra pesaría alrededor de$33.2$ libras en la luna. ¿Cuánto pesará un hombre de$150$ -libra en la luna?
Un hombre de$200$ -libra pesaría alrededor de$75.4$ libras en Marte. ¿Cuánto pesará un hombre de$150$ -libra en Marte?
Hay una$6$ posibilidad de$1$ rodar un$1$ en un dado de seis caras. ¿Cuántas veces podemos esperar que un$1$ suba en$360$ rollos del dado?
Hay una$6$ posibilidad$1$ fuera de rodar una$7$ con dos dados de seis caras. ¿Cuántas veces podemos esperar que un$7$ suba en$300$ rollos?
La proporción de cacahuetes a todos los frutos secos en una determinada marca de frutos secos mixtos envasados es$3$ a$5$. Si el paquete contiene$475$ frutos secos, ¿cuántos cacahuetes podemos esperar?
Se empaqueta una bolsa mixta de canicas con una proporción de canicas$6$ naranjas por cada canica$5$ roja. Si el paquete contiene canicas$216$ naranjas, entonces ¿cuántos mármoles rojos podemos esperar?
Un diseñador gráfico desea crear una captura$720$ de pantalla de todo el pixel. Si la relación anchura a altura va a ser$3:2$, entonces ¿a cuántos píxeles debería establecer la altura?
Si se produce un monitor de video en la relación de ancho a alto$16:9$ y el ancho del monitor es de$40$ pulgadas, entonces ¿cuál es la altura?

Contestar

1. $960$personas

3. $276$estudiantes

5. $5,000$estudiantes varones

7. $4,245,672$nacimientos

9. $8$tazas de jugo de limón

11. $24$minutos

13. $56$millas

15. $$19.50$

17. $66$orejas

19. $275$calorías

21. $24.9$libras

23. $60$tiempos

25. $285$cacahuetes

27. $480$píxeles

Ejercicio$\PageIndex{7}$ Similar Triangles

Si$ABC$ el triángulo es similar al triángulo$RST$, encuentra los dos lados restantes dada la información.

$a=6, b=8, c=10,$y$s=16$
$b=36, c=48, r=20,$y$t=32$
$b=2, c=4, r=6,$y$s=4$
$b=3, c=2, r=10,$y$t=12$
$a=40, c=50, s=3,$y$t=10$
$c=2, r=7, s=9,$y$t=4$
A la misma hora del día, un árbol proyecta una sombra$12$ de pies, mientras que un hombre de$6$ pie proyecta una sombra$3$ de pies. Estimar la altura del árbol.
A la misma hora del día, un padre y un hijo, parados uno al lado del otro, proyectaron una sombra de$4$$2$ -pie y -pie, respectivamente. Si el padre mide$6$ pies de altura, entonces ¿qué tan alto es su hijo?
Si el$6-8-10$ triángulo rectángulo$ABC$ es similar a$RST$ con un factor de escala de$\frac{2}{3}$, entonces encuentra el perímetro del triángulo$RST$.
Si el$3-4-5$ triángulo rectángulo$ABC$ es similar a$RST$ con un factor de escala de$5$, entonces encuentra el perímetro del triángulo$RST$.
Un triángulo equilátero con$6$ unidades de medición laterales es similar a otro con factor de escala$3:1$. Encuentra la longitud de cada lado del triángulo desconocido.
El perímetro de un triángulo equilátero$ABC$ mide$45$ unidades. Si triángulo$ABC ~ RST$ y$r=20$, entonces ¿cuál es el factor de escala?
El perímetro de un triángulo isósceles$ABC$, donde los dos lados iguales miden cada uno dos veces el de la base, es$60$ unidades. Si la base de un triángulo similar mide$6$ unidades, entonces encuentra su perímetro.
El perímetro de un triángulo isósceles ABC mide$11$ unidades y sus dos lados iguales miden$4$ unidades. Si el triángulo$ABC$ es similar al triángulo$RST$ y el triángulo$RST$ tiene un perímetro de$22$ unidades, entonces encuentra todos los lados del triángulo$RST$.
Un$6-8-10$ triángulo rectángulo$ABC$ es similar a un triángulo$RST$ con$72$ unidades perimetrales. Encuentra la longitud de cada pata del triángulo$RST$.
El perímetro del triángulo$ABC$ es$60$ unidades y$b=20$ unidades. Si$ABC ~ RST$ y$s=10$ unidades, entonces encuentra el perímetro del triángulo$RST$.

Contestar

1. $t = 20, r = 12$

3. $a = 3, t = 8$

5. $r = 8, b = 15$

7. $24$pies

9. $36$unidades

11. $2$unidades

13. $30$unidades

15. $r = 18$$s = 24$unidades,$t = 30$ unidades

Ejercicio$\PageIndex{8}$ Discussion Board Topics

¿Cuál es la proporción áurea y dónde aparece?
Investigar y discutir las propiedades de triángulos similares.
Discutir las matemáticas de la perspectiva.
Investigue y discuta las diversas relaciones de aspecto que están disponibles en los dispositivos de medios modernos.

Contestar

1. Las respuestas pueden variar

3. Las respuestas pueden variar