3.1: Sistema de coordenadas rectangulares
- Page ID
- 110102
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Trazar puntos usando el sistema de coordenadas rectangulares.
- Calcular la distancia entre dos puntos cualesquiera en el plano de coordenadas rectangulares.
- Determine el punto medio entre dos puntos cualesquiera.
Sistema de coordenadas rectangulares
El sistema de coordenadas rectangulares consta de dos líneas numéricas reales que se cruzan en ángulo recto. La línea numérica horizontal se llama\(x\) -axis, y la recta numérica vertical se llama\(y\) -axis. Estas dos líneas numéricas definen una superficie plana llamada plano, y cada punto en este plano está asociado con un par ordenado de números reales\((x, y)\). El primer número se llama la \(x\)coordenada -y el segundo número se llama la \(y\)coordenada -. A la intersección de los dos ejes se le conoce como origen, que corresponde al punto\((0, 0)\).
.png)
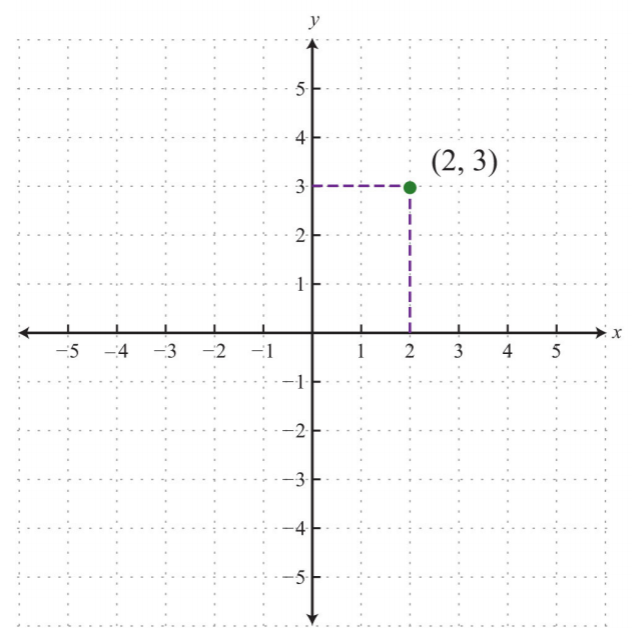
Un par ordenado\((x, y)\) representa la posición de un punto relativo al origen. La\(x\) coordenada -representa una posición a la derecha del origen si es positiva y a la izquierda del origen si es negativa. La\(y\) coordenada -representa una posición por encima del origen si es positiva y por debajo del origen si es negativa. Mediante este sistema, cada posición (punto) en el plano se identifica de manera única. Por ejemplo, el par\((2, 3)\) denota la posición relativa al origen como se muestra:
.png)
Este sistema suele llamarse sistema de coordenadas cartesianas, llamado así por el matemático francés René Descartes (1596— 1650).
Los\(y\) ejes\(x\) - y -rompen el plano en cuatro regiones llamadas cuadrantes, nombradas usando los números romanos I, II, III y IV, como se muestra en la imagen. En el cuadrante I, ambas coordenadas son positivas. En el cuadrante II, la\(x\) coordenada -es negativa y la\(y\) coordenada -positiva. En el cuadrante III, ambas coordenadas son negativas. En el cuadrante IV, la\(x\) coordenada -es positiva y la\(y\) coordenada -negativa.
.png)
Ejemplo\(\PageIndex{1}\)
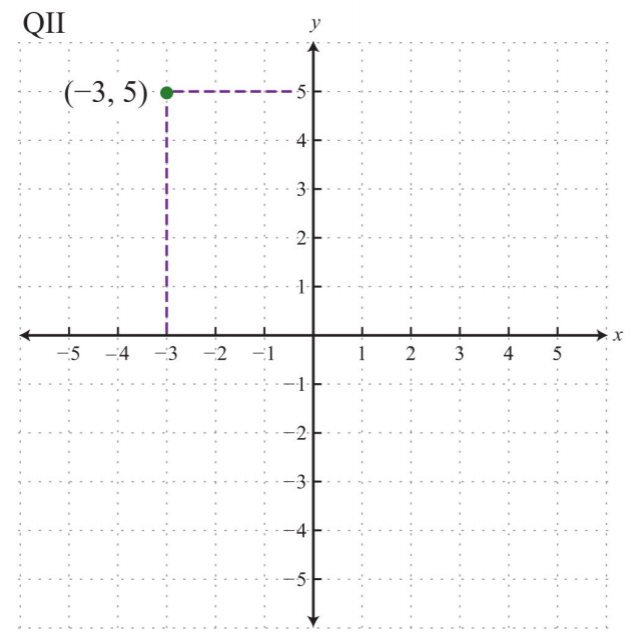
Trazar el par ordenado\((−3, 5)\) y determinar el cuadrante en el que se encuentra.
Solución:
Las coordenadas\(x=−3\) e\(y=5\) indican un punto\(3\) unidades a la izquierda de y\(5\) unidades por encima del origen.
.png)
Respuesta:
El punto se traza en el cuadrante II (QII) porque la\(x\) coordenada -es negativa y la\(y\) coordenada -positiva.
Los pares ordenados con\(0\) como una de las coordenadas no se encuentran en un cuadrante; estos puntos están en un eje u otro (o el punto es el origen si ambas coordenadas están\(0\)). Además, la escala indicada en el\(x\) eje -puede ser diferente de la escala indicada en el\(y\) eje -eje. Elija una báscula que sea conveniente para la situación dada.
Ejemplo\(\PageIndex{2}\)
Trazar este conjunto de pares ordenados:
\(\{(4, 0), (−6, 0), (0, 3), (−2, 6), (−4, −6)\}\).
Solución:
Cada marca en el\(x\) eje -representa\(2\) unidades y cada marca en el\(y\) eje representa\(3\) unidades.
.png)
Ejemplo\(\PageIndex{3}\)
Trazar este conjunto de pares ordenados:
\(\{(−6, −5), (−3, −3), (0, −1), (3, 1), (6, 3)\}\).
Solución:
.png)
En este ejemplo, los puntos parecen ser colineales, o estar en la misma línea. Todo el capítulo se enfoca en encontrar y expresar puntos con esta propiedad.
Ejercicio\(\PageIndex{1}\)
Trazar el conjunto de puntos\(\{(5, 3), (−3, 2), (−2, −4), (4, −3)\}\) e indicar en qué cuadrante se encuentran.
- Contestar
-
.png)
Figura\(\PageIndex{7}\)
Las gráficas se utilizan en la vida cotidiana para mostrar los datos visualmente. Un gráfico de líneas consiste en un conjunto de valores de datos relacionados graficados en un plano de coordenadas y conectados por segmentos de línea. Por lo general, la cantidad independiente, como el tiempo, se muestra en el\(x\) eje y la cantidad dependiente, como la distancia recorrida, en el\(y\) eje.
Ejemplo\(\PageIndex{4}\)
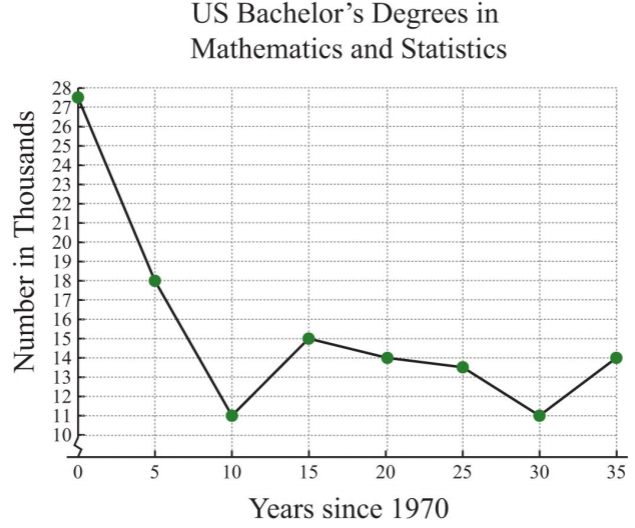
El siguiente gráfico de líneas muestra el número de licenciaturas en matemáticas y estadística otorgadas en Estados Unidos cada año desde 1970.
.png)
- ¿Cuántas licenciaturas de matemáticas y estadística se otorgaron en 1975?
- ¿En qué años se otorgó el número de títulos de matemáticas y estadística al mínimo de\(11,000\)?
Solución:
a. La escala en el\(x\) eje representa el tiempo desde 1970, por lo que para determinar el número de grados otorgados en 1975, lea el\(y\) -valor de la gráfica en\(x = 5\).
.png)
El\(y\) -valor correspondiente a\(x = 5\) es\(18\). El gráfico indica que esto es en miles; hubo grados de\(18,000\) matemáticas y estadística otorgados en 1975.
b. Para encontrar el año en que se otorgó un determinado número de títulos, primero mire el\(y\) eje -eje. En este caso, los\(11,000\) grados se representan por\(11\) en el\(y\) eje -eje; mira a la derecha para ver en qué años ocurrió esto.
.png)
El\(y\) -valor de\(11\) ocurre en dos puntos de datos, uno donde\(x = 10\) y el otro donde\(x = 30\). Estos valores corresponden a los años 1980 y 2000, respectivamente.
Respuestas:
- En el año 1975 se otorgaron grados de\(18,000\) matemáticas y estadística.
- En los años 1980 y 2000 se otorgaron los mínimos de\(11,000\) las titulaciones de matemáticas y estadística.
Fórmula de distancia
Frecuentemente es necesario calcular la distancia entre dos puntos en un plano. Para ello, formar un triángulo rectángulo usando los dos puntos como vértices del triángulo y luego aplicar el teorema de Pitágoras. Recordemos que el teorema de Pitágoras establece que si se le da algún triángulo rectángulo con patas de medición\(a\) y\(b\) unidades, entonces el cuadrado de la medida de la hipotenusa\(c\) es igual a la suma de los cuadrados de las piernas:\(a^{2}+b^{2}=c^{2}\). Es decir, la hipotenusa de cualquier triángulo rectángulo es igual a la raíz cuadrada de la suma de los cuadrados de sus patas.
.png)
Ejemplo\(\PageIndex{5}\)
Encuentra la distancia entre\((−1, 2)\) y\((3, 5)\).
Solución:
Forma un triángulo rectángulo dibujando líneas horizontales y verticales a través de los dos puntos. Esto crea un triángulo rectángulo como se muestra a continuación:
.png)
La longitud de pierna\(b\) se calcula encontrando la distancia entre los\(x\) -valores de los puntos dados, y la longitud de pierna\(a\) se calcula encontrando la distancia entre los\(y\) valores dados.
\(\begin{aligned} a&=5-2=3\text{units} \\ b&=3-(-1)=3+1=4\text{units} \end{aligned}\)
A continuación, utilice el teorema de Pitágoras para encontrar la longitud de la hipotenusa.
\(\begin{aligned} c&=\sqrt{3^{2}+4^{2}} \\ &=\sqrt{9+16} \\ &=\sqrt{25} \\ &=5\:\text{units} \end{aligned}\)
Respuesta:
La distancia entre los dos puntos es\(5\) unidades.
Generalizar este proceso para producir una fórmula que pueda ser utilizada para calcular algebraicamente la distancia entre dos puntos dados cualquiera.
.png)
Dados dos puntos,\((x_{1}, y_{1})\) y\((x_{2}, y_{2})\), luego la distancia,\(d\), entre ellos viene dada por la fórmula de distancia:
\[\sqrt{(x_{2}+x_{1})^{2}+(y_{2}+y_{1})^{2}}\]
Ejemplo\(\PageIndex{6}\)
Calcular la distancia entre\((−3, −1)\) y\((−2, 4)\).
Solución:
Usa la fórmula de distancia.
\(\begin{array}{cc} {x_{1},y_{1}}&{x_{2},y_{2}}\\{(\color{Cerulean}{-3}\color{black}{,}\color{OliveGreen}{-1}\color{black}{)}}&{(\color{Cerulean}{-2}\color{black}{,}\color{OliveGreen}{4}\color{black}{)}} \end{array}\)
Es una buena práctica incluir la fórmula en su forma general como parte de la solución escrita antes de sustituir valores por las variables. Esto mejora la legibilidad y reduce la posibilidad de errores.
\(\begin{aligned} d&=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}} \\ &=\sqrt{(\color{Cerulean}{-2}\color{black}{-(}\color{Cerulean}{-3}\color{black}{))^{2}+(}\color{OliveGreen}{4}\color{black}{-(}\color{OliveGreen}{-1}\color{black}{))^{2}}} \\ &=\sqrt{(-2+3)^{2}+(4+1)^{2}} \\ &=\sqrt{(1)^{2}+(5)^{2}} \\ &=\sqrt{1+25} \\ &=\sqrt{26} \end{aligned}\)
Respuesta:
\(\sqrt{26}\)unidades
Ejercicio\(\PageIndex{2}\)
Calcular la distancia entre\((−7, 5)\) y\((−1, 13)\).
- Contestar
-
\(10\)unidades
Ejemplo\(\PageIndex{7}\)
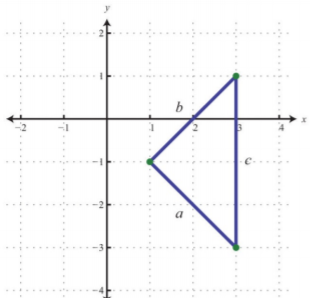
¿Los tres puntos\((1, −1), (3, −3)\), y\((3, 1)\) forman un triángulo rectángulo?
Solución:
El teorema de Pitágoras afirma que tener longitudes laterales que satisfagan la propiedad\(a^{2}+b^{2}=c^{2}\) es una condición necesaria y suficiente de los triángulos rectos. Es decir, si se puede demostrar que la suma de los cuadrados de las longitudes de las patas del triángulo es igual al cuadrado de la longitud de la hipotenusa, entonces la figura debe ser un triángulo rectángulo. Primero, calcule la longitud de cada lado usando la fórmula de distancia.
| Geometría | Cálculo |
|---|---|
.png) |
Puntos:\((1,-1)\) y\((3,-3)\) \(\begin{aligned} a&=\sqrt{(3-1)^{2}+(-3-(-1))^{2}} \\ &=\sqrt{(a)^{2}+(-3+1)^{2}} \\ &=\sqrt{4+(-2)^{2}} \\ &=\sqrt{4+4} \\ &=\sqrt{8} \end{aligned}\) |
.png) |
Puntos:\((1,-1)\) y\((3,1)\) \(\begin{aligned} b&=\sqrt{(3-1)^{2}+(1-(-1))^{2}} \\ &=\sqrt{2^{2}+(1+1)^{2}} \\ &=\sqrt{4+(2)^{2}} \\ &=\sqrt{4+4} \\ &=\sqrt{8} \end{aligned}\) |
.png) |
Puntos:\((3,-3)\) y\((3,1)\) \(\begin{aligned} c&=\sqrt{(3-3)^{2}+(1-(-3))^{2}} \\ &=\sqrt{(0)^{2}+(1+3)^{2}} \\ &=\sqrt{0+(4)^{2}} \\ &=\sqrt{16} \\ &=4 \end{aligned}\) |
Ahora comprobamos para ver si\(a^{2}+b^{2}=c^{2}\).
\(a^{2}+b^{2}=c^{2}\)
\(\begin{aligned} (\sqrt{8})^{2}+(\sqrt{8})^{2}&=(4)^{2} \\ \sqrt{64}+\sqrt{64}&=16 \\ 8+8&=16\\16&=16\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Respuesta:
Sí, los tres puntos forman un triángulo rectángulo. De hecho, dado que dos de las patas son iguales en longitud, los puntos forman un triángulo rectángulo isósceles.
Fórmula de punto medio
El punto que bisecciona el segmento de línea formado por dos puntos\((x_{2}, y_{2})\),\((x_{1}, y_{1})\) y, se denomina punto medio y viene dado por la siguiente fórmula:
\[ \left( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right) \]
El punto medio es un par ordenado formado al encontrar el promedio de los\(x\) -valores y el promedio de los\(y\) -valores de los puntos dados.
Ejemplo\(\PageIndex{8}\)
Calcular el punto medio entre\((−1, −2)\) y\((7, 4)\).
Solución:
Primero, calcule el promedio de los\(y\) valores\(x\) - y -de los puntos dados.
\(\begin{array}{cc} {(x_{1},y_{1})}&{(x_{2},y_{2})}\\{(-1,-2)}&{(7,4)} \end{array}\)
\(\begin{aligned} \frac{x_{1}+x_{2}}{2}&=\frac{-1+7}{2}&=\frac{6}{2}&=3 \\ \frac{y_{1}+y_{2}}{2}&=\frac{-2+4}{2}&=\frac{2}{2}&=1 \end{aligned}\)
A continuación, forme el punto medio como un par ordenado usando las coordenadas promediadas.
\(\left( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right)\)
\((3,1)\)
Respuesta:
\((3,1)\)
Para verificar que éste es efectivamente el punto medio, calcule la distancia entre los dos puntos dados y verifique que el resultado sea igual a la suma de las dos distancias iguales desde los puntos finales hasta este medio punto. Esta verificación se deja al lector como ejercicio.
.png)
Ejercicio\(\PageIndex{3}\)
Encuentra el punto medio entre\((−6, 5)\) y\((6, −11)\).
- Contestar
-
\((0,-3)\)
Claves para llevar
- Utilice el sistema de coordenadas rectangulares para identificar de forma única puntos en un plano usando pares ordenados\((x, y)\). Los pares ordenados indican posición relativa al origen. La\(x\) coordenada -indica la posición a la izquierda y derecha del origen. La\(y\) coordenada -indica la posición por encima o por debajo del origen.
- Las escalas en el\(x\) eje y el\(y\) eje pueden ser diferentes. Elija una escala para cada eje que sea apropiada para el problema dado.
- Los gráficos se utilizan para visualizar datos del mundo real. Por lo general, los datos independientes están asociados con el\(x\) eje -y los datos dependientes están asociados con el\(y\) eje.
- El teorema de Pitágoras nos da una condición necesaria y suficiente de triángulos rectos. Dado un triángulo rectángulo, entonces las medidas de los lados satisfacen\(a^{2}+b^{2}=c^{2}\). Por el contrario, si los lados satisfacen\(a^{2}+b^{2}=c^{2}\), entonces el triángulo debe ser un triángulo rectángulo.
- La fórmula de distancia\(d=\sqrt{(x_{2}−x_{1})^{2}+(y_{2}−y_{1})^{2}}\),, se deriva del teorema de Pitágoras y nos da la distancia entre dos puntos cualesquiera,\((x_{1}, y_{1})\) y\((x_{2}, y_{2})\), en un plano de coordenadas rectangulares.
- La fórmula de punto medio\(\left( \frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} \right)\),, se deriva tomando el promedio de cada coordenada y formando un par ordenado.
Ejercicio\(\PageIndex{4}\) Ordered Pairs
Dar las coordenadas de puntos\(A, B, C, D,\) y\(E\).
1.
.png)
2.
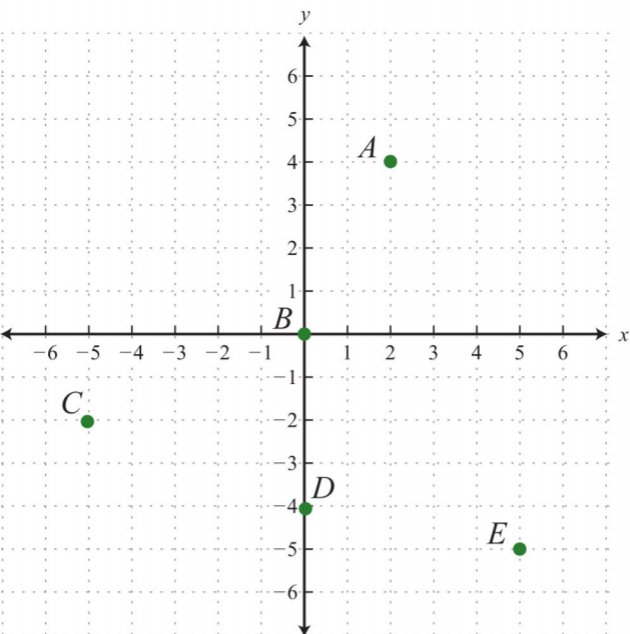.png)
3.
.png)
4.
.png)
5.
.png)
6.
.png)
- Contestar
-
1. \(A: (3, 5); B: (−2, 3); C: (−5, 0); D: (1, −3); E: (−3, −4)\)
3. \(A: (0, 6); B: (−4, 3); C: (−8, 0); D: (−6, −6); E: (8, −9)\)
5. \(A: (−10, 25); B: (30, 20); C: (0, 10); D: (15, 0); E: (25, −10)\)
Ejercicio\(\PageIndex{5}\) Ordered Pairs
Grafica el conjunto dado de pares ordenados.
- \(\{(−4, 5), (−1, 1), (−3, −2), (5, −1)\}\)
- \(\{(−15, −10), (−5, 10), (15, 10), (5, −10)\}\)
- \(\{(−2, 5), (10, 0), (2, −5), (6, −10)\}\)
- \(\{(−8, 3), (−4, 6), (0, −6), (6, 9)\}\)
- \(\{(−10, 5), (20, −10), (30, 15), (50, 0)\}\)
- \(\{(−\frac{5}{3}, −\frac{1}{2}),(−\frac{1}{3}, \frac{1}{2}),(\frac{2}{3}, −1),(\frac{5}{3}, 1)\}\)
- \(\{(−\frac{3}{5}, −\frac{4}{3}),(\frac{2}{5}, \frac{4}{3}),(1, −\frac{2}{3}),(0, 1)\}\)
- \(\{(−3.5, 0), (−1.5, 2), (0, 1.5), (2.5, −1.5)\}\)
- \(\{(−0.8, 0.2), (−0.2, −0.4), (0, −1), (0.6, −0.4)\}\)
- \(\{(−1.2, −1.2), (−0.3, −0.3), (0, 0), (0.6, 0.6), (1.2, 1.2)\}\)
- Contestar
-
1.
.png)
Figura\(\PageIndex{24}\) 3.
.png)
Figura\(\PageIndex{25}\) 5.
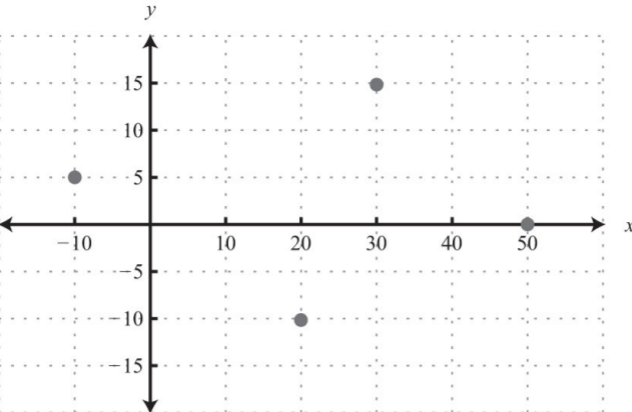.png)
Figura\(\PageIndex{26}\) 7.
.png)
Figura\(\PageIndex{27}\) 9.
.png)
Figura\(\PageIndex{28}\)
Ejercicio\(\PageIndex{6}\) Ordered Pairs
Indicar el cuadrante en el que se encuentra el punto dado.
- \((−3, 2)\)
- \((5, 7)\)
- \((−12, −15)\)
- \((7, −8)\)
- \((−3.8, 4.6)\)
- \((17.3, 1.9)\)
- \((−\frac{1}{8}, −\frac{5}{8})\)
- \((\frac{3}{4}, −\frac{1}{4})\)
- \(x>0\)y\(y<0\)
- \(x<0\)y\(y<0\)
- \(x<0\)y\(y>0\)
- \(x>0\)y\(y>0\)
- Contestar
-
1. QII
3. QIII
5. QII
7. QIII
9. QIV
11. QII
Ejercicio\(\PageIndex{7}\) Ordered Pairs
El precio promedio de un galón de gasolina sin plomo regular en ciudades de Estados Unidos se da en la siguiente gráfica de líneas. Utilice la gráfica para responder a las siguientes preguntas.
.png)
- ¿Cuál fue el precio promedio de un galón de gasolina sin plomo en 2004?
- ¿Cuál fue el precio promedio de un galón de gasolina sin plomo en 1976?
- ¿En qué años fue el precio promedio de un galón de gasolina sin plomo $\(1.20\)?
- ¿Cuál es el incremento de precio de un galón de gasolina de 1980 a 2008?
- ¿Cuál fue el incremento porcentual en el precio de un galón de gasolina sin plomo de 1976 a 1980?
- ¿Cuál fue el incremento porcentual en el precio de un galón de gasolina sin plomo de 2000 a 2008?
- Contestar
-
1. $\(1.80\)
3. 1980 a 1984, 1996
3. \(100\)%
Ejercicio\(\PageIndex{8}\) Ordered Pairs
El precio promedio de la harina blanca para todo uso en ciudades de Estados Unidos de 1980 a 2008 se da en la siguiente gráfica de líneas. Usa la gráfica para responder a las preguntas que siguen.
.png)
- ¿Cuál fue el precio promedio por libra de harina blanca para todo uso en el año 2000?
- ¿Cuál fue el precio promedio por libra de harina blanca multiusos en 2008?
- ¿En qué año el precio de la harina promedió $\(0.25\) por libra?
- ¿En qué años el precio de la harina promedió $\(0.20\) por libra?
- ¿Cuál fue el incremento porcentual de la harina del año 2000 al 2008?
- ¿Cuál fue el incremento porcentual de la harina del año 1992 al 2000?
- Contestar
-
1. $\(0.30\)
3. 1992
5. \(67\)%
Ejercicio\(\PageIndex{9}\) Ordered Pairs
Dados los siguientes datos, cree un gráfico de líneas.
1. El porcentaje del total de egresados de preparatoria que se matricularon en la universidad.
| Año | Porcentaje |
|---|---|
| 1969 | \(36\)% |
| 1979 | \(40\)% |
| 1989 | \(47\)% |
| 1999 | \(42\)% |
2. La temperatura media diaria dada en grados Fahrenheit en mayo.
| Examen | Temperatura |
|---|---|
| 8:00am | \(60\) |
| 12:00pm | \(72\) |
| 4:00pm | \(75\) |
| 8:00pm | \(67\) |
| 12:00am | \(60\) |
| 4:00am | \(55\) |
- Contestar
-
1.
.png)
Figura\(\PageIndex{31}\)
Ejercicio\(\PageIndex{10}\) Ordered Pairs
Calcular el área de la forma formada conectando el siguiente conjunto de vértices.
- \(\{(0, 0), (0, 3), (5, 0), (5, 3)\}\)
- \(\{(−1, −1), (−1, 1), (1, −1), (1, 1)\}\)
- \(\{(−2, −1), (−2, 3), (5, 3), (5, −1)\}\)
- \(\{(−5, −4), (−5, 5), (3, 5), (3, −4)\}\)
- \(\{(0, 0), (4, 0), (2, 2)\}\)
- \(\{(−2, −2), (2, −2), (0, 2)\}\)
- \(\{(0, 0), (0, 6), (3, 4)\}\)
- \(\{(−2, 0), (5, 0), (3, −3)\}\)
- Contestar
-
1. \(15\)unidades cuadradas
3. \(28\)unidades cuadradas
5. \(4\)unidades cuadradas
7. \(9\)unidades cuadradas
Ejercicio\(\PageIndex{11}\) Distance Formula
Calcular la distancia entre los dos puntos dados.
- \((−5, 3)\)y\((−1, 6)\)
- \((6, −2)\)y\((−2, 4)\)
- \((0, 0)\)y\((5, 12)\)
- \((−6, −8)\)y\((0, 0)\)
- \((−7, 8)\)y\((5, −1)\)
- \((−1, −2)\)y\((9, 22)\)
- \((−1, 2)\)y\((−\frac{7}{2}, −4)\)
- \((−\frac{1}{2}, \frac{1}{3})\)y\((\frac{5}{2}, −\frac{11}{3})\)
- \((−\frac{1}{3}, \frac{2}{3})\)y\((1, −\frac{1}{3})\)
- \((\frac{1}{2}, −\frac{3}{4})\)y\((\frac{3}{2}, \frac{1}{4})\)
- \((1, 2)\)y\((4, 3)\)
- \((2, −4)\)y\((−3, −2)\)
- \((−1, 5)\)y\((1, −3)\)
- \((1, −7)\)y\((5, −1)\)
- \((−7, −3)\)y\((−1, 6)\)
- \((0, 1)\)y\((1, 0)\)
- \((−0.2, −0.2)\)y\((1.8, 1.8)\)
- \((1.2, −3.3)\)y\((2.2, −1.7)\)
- Contestar
-
1. \(5\)unidades
3. \(13\)unidades
5. \(15\)unidades
7. \(\frac{13}{2}\)unidades
9. \(\frac{5}{3}\)unidades
11. \(\sqrt{10}\)unidades
13. \(2\sqrt{17}\)unidades
15. \(3\sqrt{13}\)unidades
17. \(2.8\)unidades
Ejercicio\(\PageIndex{12}\) Distance Formula
Para cada problema, mostrar que los tres puntos forman un triángulo rectángulo.
- \((−3, −2), (0, −2),\)y\((0, 4)\)
- \((7, 12), (7, −13),\)y\((−5, −4)\)
- \((−1.4, 0.2), (1, 2),\)y\((1, −3)\)
- \((2, −1), (−1, 2),\)y\((6, 3)\)
- \((−5, 2), (−1, −2),\)y\((−2, 5)\)
- \((1, −2), (2, 3),\)y\((−3, 4)\)
- Contestar
-
1. Prueba
3. Prueba
5. Prueba
Ejercicio\(\PageIndex{13}\) Distance Formula
Los triángulos isósceles tienen dos patas de igual longitud. Para cada problema, mostrar que los siguientes puntos forman un triángulo isósceles.
- \((1, 6), (−1, 1),\)y\((3, 1)\)
- \((−6, −2), (−3, −5),\)y\((−9, −5)\)
- \((−3, 0), (0, 3),\)y\((3, 0)\)
- \((0, −1), (0, 1),\)y\((1, 0)\)
- Contestar
-
1. Prueba
3. Prueba
Ejercicio\(\PageIndex{14}\) Distance Formula
Calcular el área y el perímetro de los triángulos formados por el siguiente conjunto de vértices.
- \(\{(−4, −5), (−4, 3), (2, 3)\}\)
- \(\{(−1, 1), (3, 1), (3, −2)\}\)
- \(\{(−3, 1), (−3, 5), (1, 5)\}\)
- \(\{(−3, −1), (−3, 7), (1, −1)\}\)
- Contestar
-
1. Perímetro:\(24\) unidades; área: unidades\(24\) cuadradas
3. Perímetro:\(8+4\sqrt{2}\) unidades; área: unidades\(8\) cuadradas
Ejercicio\(\PageIndex{15}\) Midpoint Formula
Encuentra el punto medio entre los dos puntos dados.
- \((−1, 6)\)y\((−7, −2) \)
- \((8, 0)\)y\((4, −3) \)
- \((−10, 0)\)y\((10, 0) \)
- \((−3, −6)\)y\((−3, 6) \)
- \((−10, 5)\)y\((14, −5) \)
- \((0, 1)\)y\((2, 2) \)
- \((5, −3)\)y\((4, −5) \)
- \((0, 0)\)y\((1, 1) \)
- \((−1, −1)\)y\((4, 4) \)
- \((3, −5)\)y\((3, 5) \)
- \((−\frac{1}{2}, −\frac{1}{3})\)y\((\frac{3}{2}, \frac{7}{3})\)
- \((\frac{3}{4}, −\frac{2}{3})\)y\((\frac{1}{8}, −\frac{1}{2})\)
- \((\frac{5}{3}, \frac{1}{4})\)y\((−\frac{1}{6}, −\frac{3}{2})\)
- \((−\frac{1}{5}, −\frac{5}{2})\)y\((\frac{7}{10}, −\frac{1}{4})\)
- Dado el triángulo rectángulo formado por los vértices\((0, 0), (6, 0),\) y\((6, 8)\), muestran que los puntos medios de los lados forman un triángulo rectángulo.
- Dado el triángulo isósceles formado por los vértices\((−10, −12), (0, 12),\) y\((10, −12)\), muestran que los puntos medios de los lados también forman un triángulo isósceles.
- Calcular el área del triángulo formado por los vértices\((−4, −3), (−1, 1),\) y\((2, −3)\). (Sugerencia: Los vértices forman un triángulo isósceles.)
- Calcular el área del triángulo formado por los vértices\((−2, 1), (4, 1),\) y\((1, −5)\).
- Contestar
-
1. \((−4, 2)\)
3. \((0, 0)\)
5. \((2, 0)\)
7. \((\frac{9}{2}, −4)\)
9. \((\frac{3}{2}, \frac{3}{2})\)
11. \((\frac{1}{2}, 1)\)
13. \((\frac{3}{4}, −\frac{5}{8})\)
15. \(12\)unidades cuadradas
Ejercicio\(\PageIndex{16}\) Discussion Board Topics
- Investigar y discutir la vida y contribuciones a las matemáticas de René Descartes.
- Investigar y discutir la historia del triángulo rectángulo y el teorema de Pitágoras.
- ¿Qué es un triple pitagórico? Proporcione algunos ejemplos.
- Explica por qué no puedes usar una regla para calcular la distancia en una gráfica.
- ¿Cómo se divide un segmento de línea con solo una brújula y una recta?
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar
5. Las respuestas pueden variar


