3.2: Gráfica por puntos de trazado

Última actualización
Guardar como PDF

Page ID: 110105

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Verificar soluciones a ecuaciones lineales con dos variables.
Gráfica líneas trazando puntos.
Identificar y graficar líneas horizontales y verticales.

Soluciones a Ecuaciones con Dos Variables

Una ecuación lineal con dos variables tiene forma estándar$ax+by=c$, donde$a,b$, y$c$ son números reales y$a$ y no$b$ son ambos$0$. Las soluciones a ecuaciones de esta forma son pares ordenados$(x, y)$, donde las coordenadas, cuando se sustituyen en la ecuación, producen una declaración verdadera.

Ejemplo$\PageIndex{1}$

Determinar si$(1, −2)$ y$(−4, 1)$ son soluciones para$6x−3y=12$.

Solución:

Sustituya los$y$ valores$x$ - y -en la ecuación para determinar si el par ordenado produce una declaración verdadera.

$\begin{array}{c|c}{\underline{Check\:\:(1,-2)}}&{\underline{Check\:\:(-4,1)}}\\{6x-3y=12}&{6x-3y=12} \\{6(\color{OliveGreen}{1}\color{black}{)-3(}\color{OliveGreen}{-2}\color{black}{)=12}}&{6(\color{OliveGreen}{-4}\color{black}{)-3(}\color{OliveGreen}{1}\color{black}{)=12}}\\{6+6=12}&{-24-3=12}\\{12=12\quad\color{Cerulean}{\checkmark}}&{-27=12\quad\color{red}{x}}\end{array}$

Respuesta:

$(1,-2)$es una solución, y no$(-4,1)$ lo es.

A menudo ocurre que una ecuación lineal se da en una forma donde una de las variables, generalmente$y$, está aislada. Si este es el caso, entonces podemos comprobar que un par ordenado es una solución sustituyendo en un valor una de las coordenadas y simplificando para ver si obtenemos la otra.

Ejemplo$\PageIndex{2}$

¿Son$(\frac{1}{2}, −3)$ y$(−5, 14)$ soluciones para$y=2x−4$?

Solución:

Sustituir los$x$ valores -y simplificar para ver si se obtienen$y$ los valores -correspondientes.

$\begin{array}{c|c} {\underline{x=\frac{1}{2}}}&{\underline{x=-5}}\\{y=2x-4}&{y=2x-4}\\{=2\color{black}{\left(\color{OliveGreen}{\frac{1}{2}} \right)-4}}&{=2(\color{OliveGreen}{-5}\color{black}{)-4}}\\{=1-4}&{=-10-4}\\{=-3\quad\color{Cerulean}{\checkmark}}&{=-14\quad\color{red}{x}} \end{array}$

Respuesta:

$(\frac{1}{2},-3)$es una solución, y no$(-5,14)$ lo es.

Ejercicio$\PageIndex{1}$

¿Es$(6, −1)$ una solución para$y=−\frac{2}{3}x+3$?

Responder: Sí

Cuando se dan ecuaciones lineales con dos variables, podemos resolver para una de las variables, generalmente$y$, y obtener una ecuación equivalente de la siguiente manera:

Escrito en esta forma, podemos ver que$y$ depende de$x$. Aquí$x$ está la variable independiente y$y$ es la variable dependiente.

$\left. \begin{aligned} 6x-3y&=12 \\ y&=2x-4\end{aligned}\right\} \color{Cerulean}{Equivalent\:equations}$

La ecuación lineal se$y=2x−4$ puede utilizar para encontrar soluciones de pares ordenados. Si sustituimos cualquier número real por$x$, entonces podemos simplificar para encontrar el valor y correspondiente. Por ejemplo, si$x=3$, entonces$y=2(3)−4=6−4=2$, y podemos formar una solución de par ordenado,$(3, 2)$. Dado que hay infinitamente muchos números reales para elegir$x$, la ecuación lineal tiene infinitamente muchas soluciones de pares ordenados$(x, y)$.

Ejemplo$\PageIndex{3}$

Encuentre soluciones de pares ordenados a la ecuación$5x−y=14$ con los$x$ valores -dados$\{−2, −1, 0, 4, 6\}$.

Solución:

Primero, resolver para$y$.

A continuación, sustituya los$x$ valores -en la ecuación$y=5x−14$ para encontrar los$y$ valores -correspondientes.

$x-value$$y-value$$Solution$$x=-2$$(-2,-24)$$x=-1$$(-1,-19)$$x=0$$(0,-14)$$x=4$$(4,6)$$x=6$$(6,16)$ Mesa$\PageIndex{1}$

Respuesta:

$\{(−2, −24), (−1, −19), (0, −14), (4, 6), (6, 16)\}$

En el ejemplo anterior, se dan ciertos$x$ -valores, pero ese no siempre va a ser el caso. Al tratar$x$ como la variable independiente, podemos elegir cualquier valor para$x$ y luego sustituirlos en la ecuación para encontrar los$y$ valores correspondientes. Este método produce tantas soluciones de pares ordenados como deseamos.

Ejemplo$\PageIndex{4}$

Encuentre cinco soluciones de pares ordenados para$6x+2y=10$.

Solución:

Primero, resolver para$y$.

$\begin{aligned} 6x+2y&=10 \\ 6x+2y\color{Cerulean}{-6x}&=10\color{Cerulean}{-6x} \\ 2y&=-6x+10 \\ \frac{2y}{\color{Cerulean}{2}}&=\frac{-6x+10}{\color{Cerulean}{2}} \\ y&=\frac{-6x}{2}+\frac{10}{2} \\ y&=-3x+5 \end{aligned}$

A continuación, elija cualquier conjunto de$x$ -valores. Por lo general, elegimos algunos valores negativos y algunos valores positivos. En este caso, encontraremos los$y$ -valores correspondientes cuando$x$ es$\{−2, −1, 0, 1, 2\}$. Haga las sustituciones necesarias para rellenar la siguiente tabla (a menudo denominada gráfico t):

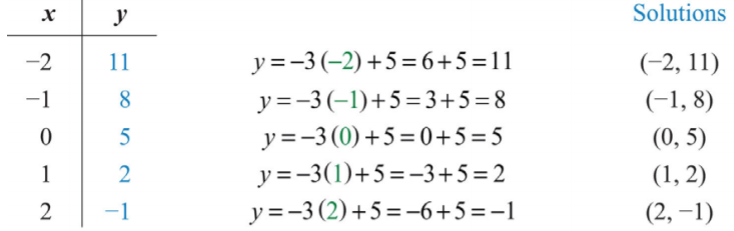Captura de pantalla (489) .png — Figura$\PageIndex{1}$

Respuesta:

$\{(−2, 11), (−1, 8), (0, 5), (1, 2), (2, −1)\}$. Dado que hay infinitamente muchas soluciones de pares ordenados, las respuestas pueden variar dependiendo de la elección de valores para la variable independiente.

Ejercicio$\PageIndex{2}$

Encuentre cinco soluciones de pares ordenados para$10x−2y=2$.

Responder: $\{(−2, −11), (−1, −6), (0, −1), (1, 4), (2, 9)\}$(las respuestas pueden variar)

Gráfica por puntos de trazado

Dado que las soluciones a las ecuaciones lineales son pares ordenados, se pueden graficar usando el sistema de coordenadas rectangulares. El conjunto de todas las soluciones a una ecuación lineal se puede representar en un plano de coordenadas rectangulares usando una línea recta que conecta al menos dos puntos; esta línea se llama su gráfica. Para ilustrar esto, graficar cinco soluciones de pares ordenados$\{(−2, 11), (−1, 8), (0, 5), (1, 2), (2, −1)\}$,, a la ecuación lineal$6x+2y=10$.

Captura de pantalla (490) .png — Figura$\PageIndex{2}$

Observe que los puntos son colineales; este será el caso de cualquier ecuación lineal. Dibuja una línea a través de los puntos con una recta, y agrega flechas en cada extremo para indicar que la gráfica se extiende indefinidamente.

Captura de pantalla (491) .png — Figura$\PageIndex{3}$

La línea resultante representa todas las soluciones a$6x+2y=10$, de las cuales hay infinitamente muchas. Los pasos para graficar líneas trazando puntos se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{5}$

Encuentre cinco soluciones de pares ordenados y grafique:

$10x−5y=10$.

Solución:

S tep 1: Resolver para$y$.

Paso 2: Elija al menos dos$x$ -valores y encuentre los$y$ valores -correspondientes. En esta sección, elegiremos cinco números reales para usar como$x$ -valores. Es una buena práctica elegir$0$ y algunos números negativos, así como algunos números positivos.

Captura de pantalla (493) .png — Figura$\PageIndex{4}$

No siempre será el caso que se$y$ pueda resolver en términos de$x$ con coeficientes enteros. De hecho, los coeficientes a menudo resultan ser fracciones.

Ejemplo$\PageIndex{6}$

Encuentre cinco soluciones de pares ordenados y grafique:

$−5x+2y=10$.

Solución:

$\begin{aligned} -5x+2y&=10 \\ -5x+2y\color{Cerulean}{+5x}&=10\color{Cerulean}{+5x} \\ 2y&=5x+10 \\ frac{2y}{\color{Cerulean}{2}}&=\frac{5x+10}{\color{Cerulean}{2}} \\ y&=\frac{5x}{2}+\frac{10}{2} \\ y&=\frac{5}{2}x+5 \end{aligned}$

Recuerda que puedes elegir cualquier número real para la variable independiente$x$, así que elige sabiamente aquí. Dado que el denominador del coeficiente de la variable$x$ es$2$, se pueden evitar fracciones eligiendo múltiplos de$2$ para los$x$ -valores. En este caso, elija el conjunto de$x$ -valores$\{−6, −4, −2, 0, 2\}$ y encuentre los$y$ -valores correspondientes.

Captura de pantalla (494) .png — Figura$\PageIndex{6}$

Cinco soluciones son$\{(−6, −10), (−4, −5), (−2, 0), (0, 5), (2, 10)\}$. Aquí elegimos escalar el$x$ eje -con múltiplos de$2$ y el$y$ -eje con múltiplos de$5$.

Respuesta:

Captura de pantalla (495) .png — Figura$\PageIndex{7}$

Ejercicio$\PageIndex{3}$

Encuentra cinco soluciones de pares ordenados y grafica:$x+2y=6$.

Responder: $\{(−2, 4), (0, 3), (2, 2), (4, 1), (6, 0)\}$

$Captura de pantalla (496) .png$
Figura$\PageIndex{8}$

Líneas horizontales y verticales

Necesitamos reconocer por inspección ecuaciones lineales que representan una línea vertical u horizontal.

Ejemplo$\PageIndex{7}$

Gráfica trazando cinco puntos:$y=−2$.

Solución:

Dado que la ecuación dada no tiene una variable$x$, podemos reescribirla con un$0$ coeficiente para$x$.

$y=0x-2$

Elija cinco valores cualesquiera para$x$ y vea que el$y$ -valor correspondiente es siempre$−2$.

Captura de pantalla (497) .png — Figura$\PageIndex{9}$

Ahora tenemos cinco soluciones de pares ordenadas para trazar$\{(−2, −2), (−1, −2), (0, −2), (1, −2), (2, −2)\}$.

Respuesta:

Captura de pantalla (498) .png — Figura$\PageIndex{10}$

Cuando el coeficiente para la variable$x$ es$0$, la gráfica es una línea horizontal. En general, la ecuación para una línea horizontal se puede escribir en la forma$y=k$, donde$k$ representa cualquier número real.

Ejemplo$\PageIndex{8}$

Gráfica trazando cinco puntos:$x = 3$.

Solución:

Dado que la ecuación dada no tiene una variable$y$, reescribirla con un$0$ coeficiente para$y$.

$x=0y+3$

Elija cinco valores cualesquiera para$y$ y vea que el$x$ -valor correspondiente es siempre$3$.

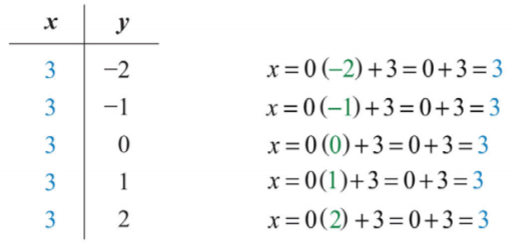Captura de pantalla (499) .png — Figura$\PageIndex{11}$

Ahora tenemos cinco soluciones de pares ordenadas para trazar:$\{(3, −2), (3, −1), (3, 0), (3, 1), (3, 2)\}$.

Respuesta:

Captura de pantalla (500) .png — Figura$\PageIndex{12}$

Cuando el coeficiente para la variable$y$ es$0$, la gráfica es una línea vertical. En general, la ecuación para una línea vertical se puede escribir como$x=k$, donde$k$ representa cualquier número real.

Para resumir, si$k$ es un número real.

\[y=k\quad\color{Cerulean}{Horizontal\:line}\]

\[x=k\quad\color{Cerulean}{Vertical\:line}\]

Ejercicio$\PageIndex{4}$

Gráfica$y=5$ y$x=−2$ sobre el mismo conjunto de ejes y determina dónde se cruzan.

Responder: $(-2,5)$

Claves para llevar

Las soluciones a ecuaciones lineales con dos variables$ax+by=c$ son pares ordenados$(x, y)$, donde las coordenadas, cuando se sustituyen en la ecuación, dan como resultado una declaración verdadera.
Las ecuaciones lineales con dos variables tienen infinitamente muchas soluciones de pares ordenados. Cuando se grafican las soluciones, son colineales.
Para encontrar soluciones de pares ordenados, elija valores para la variable independiente, generalmente$x$, y sustituirlos en la ecuación para encontrar los$y$ valores -correspondientes.
Para graficar ecuaciones lineales, determine al menos dos soluciones de pares ordenados y dibuje una línea a través de ellas con una recta.
Las líneas horizontales son descritas por$y = k$, donde$k$ está cualquier número real.
Las líneas verticales se describen por$x = k$, donde$k$ está cualquier número real.

Ejercicio$\PageIndex{5}$ Solutions to Linear Systems

Determinar si el punto dado es una solución.

$5x−2y=4; (−1, 1)$
$3x−4y=10; (2, −1)$
$−3x+y=−6; (4, 6)$
$−8x−y=24; (−2, −3)$
$−x+y=−7; (5, −2)$
$9x−3y=6; (0, −2)$
$\frac{1}{2}x+\frac{1}{3}y=−\frac{1}{6}; (1, −2)$
$\frac{3}{4}x−\frac{1}{2}y=−1; (2, 1)$
$4x−3y=1; (\frac{1}{2}, \frac{1}{3})$
$−10x+2y=−\frac{9}{5}; (\frac{1}{5}, \frac{1}{10})$
$y=\frac{1}{3}x+3; (6, 3)$
$y=−4x+1; (−2, 9)$
$y=\frac{2}{3}x−3; (0, −3)$
$y=−\frac{5}{8}x+1; (8, −5)$
$y=−\frac{1}{2}x+\frac{3}{4}; (−\frac{1}{2}, 1)$
$y=−\frac{1}{3}x−\frac{1}{2}; (\frac{1}{2}, −\frac{2}{3})$
$y=2; (−3, 2)$
$y=4; (4, −4)$
$x=3; (3, −3)$
$x=0; (1, 0)$

Responder

1. No

3. Sí

5. Sí

7. Sí

9. Sí

11. No

13. Sí

15. Sí

17. Sí

19. Sí

Ejercicio$\PageIndex{6}$ Solutions to Linear Systems

Encuentre las soluciones de pares ordenados dado el conjunto de$x$ -valores.

$y=−2x+4; \{−2, 0, 2\}$
$y=12x−3; \{−4, 0, 4\}$
$y=−\frac{3}{4}x+\frac{1}{2}; \{−2, 0, 2\}$
$y=−3x+1; \{−\frac{1}{2}, 0, \frac{1}{2}\}$
$y=−4; \{−3, 0, 3\}$
$y=\frac{1}{2}x+\frac{3}{4}; \{−\frac{1}{4}, 0, \frac{1}{4}\}$
$2x−3y=1; \{0, 1, 2\}$
$3x−5y=−15; \{−5, 0, 5\}$
$–x+y=3; \{−5, −1, 0\}$
$\frac{1}{2}x−\frac{1}{3}y=−4; \{−4, −2, 0\}$
$\frac{3}{5}x+\frac{1}{10}y=2; \{−15, −10, −5\}$
$x−y=0; \{10, 20, 30\}$

Responder

1. $\{(−2, 8), (0, 4), (2, 0)\}$

3. $\{(−2, 2), (0, 1/2), (2, −1)\}$

5. $\{(−3, −4), (0, −4), (3, −4)\}$

7. $\{(0, −\frac{1}{3}), (1, \frac{1}{3}), (2, 1)\}$

9. $\{(−5, −2), (−1, 2), (0, 3)\}$

11. $\{(−15, 110), (−10, 80), (−5, 50)\}$

Ejercicio$\PageIndex{7}$ Solutions to Linear Systems

Encuentre las soluciones de pares ordenadas, dado el conjunto de$y$ -valores.

$y=\frac{1}{2}x−1; \{−5, 0, 5\}$
$y=−\frac{3}{4}x+2; \{0, 2, 4\}$
$3x−2y=6; \{−3, −1, 0\}$
$−x+3y=4; \{−4, −2, 0\}$
$\frac{1}{3}x−\frac{1}{2}y=−4; \{−1, 0, 1\}$
$\frac{3}{5}x+\frac{1}{10}y=2; \{−20, −10, −5\}$

Responder

1. $\{(−8, −5), (2, 0), (12, 5)\}$

3. $\{(0, −3), (\frac{4}{3}, −1), (2, 0)\}$

5. $\{(−\frac{27}{2}, −1), (−12, 0), (−\frac{21}{2}, 1)\}$

Ejercicio$\PageIndex{8}$ Graphing Lines

Dado el conjunto de$x$ -valores$\{−2, −1, 0, 1, 2\}$, busque los$y$ valores -correspondientes y graficarlos.

$y=x+1$
$y=−x+1$
$y=2x−1$
$y=−3x+2$
$y=5x−10$
$5x+y=15$
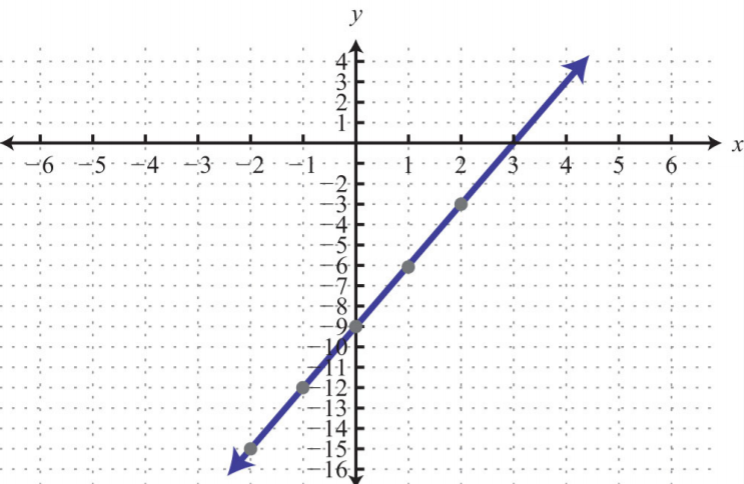
$3x−y=9$
$6x−3y=9$
$y=−5$
$y=3$

Responder

Captura de pantalla (501) .png — Figura$\PageIndex{13}$

Captura de pantalla (502) .png — Figura$\PageIndex{14}$

Captura de pantalla (503) .png — Figura$\PageIndex{15}$

Captura de pantalla (504) .png — Figura$\PageIndex{16}$

Captura de pantalla (506) .png — Figura$\PageIndex{17}$

Ejercicio$\PageIndex{9}$ Graphing Lines

Encuentra al menos cinco soluciones de pares ordenados y grafica.

$y=2x−1$
$y=−5x+3$
$y=−4x+2$
$y=10x−20$
$y=−\frac{1}{2}x+2$
$y=\frac{1}{3}x−1$
$y=\frac{2}{3}x−6$
$y=−\frac{2}{3}x+2$
$y=x$
$y=−x$
$−2x+5y=−15$
$x+5y=5$
$6x−y=2$
$4x+y=12$
$−x+5y=0$
$x+2y=0$
$\frac{1}{10}x−y=3$
$\frac{3}{2}x+5y=30$

Responder

Captura de pantalla (507) .png — Figura$\PageIndex{18}$

Captura de pantalla (508) .png — Figura$\PageIndex{19}$

Captura de pantalla (509) .png — Figura$\PageIndex{20}$

Captura de pantalla (510) .png — Figura$\PageIndex{21}$

Captura de pantalla (511) .png — Figura$\PageIndex{22}$

11.

Captura de pantalla (512) .png — Figura$\PageIndex{23}$

13.

Captura de pantalla (513) .png — Figura$\PageIndex{24}$

15.

Captura de pantalla (514) .png — Figura$\PageIndex{25}$

17.

Captura de pantalla (515) .png — Figura$\PageIndex{26}$

Ejercicio$\PageIndex{10}$ Horizontal and Vertical Lines

Encuentre al menos cinco soluciones de pares ordenadas y gráfiquelas.

$y=4$
$y=−10$
$x=4$
$x=−1$
$y=0$
$x=0$
$y=\frac{3}{4}$
$x=−\frac{5}{4}$
Grafica las líneas$y=−4$ y$x=2$ en el mismo conjunto de ejes. ¿Dónde se cruzan?
Grafica las líneas$y=5$ y$x=−5$ en el mismo conjunto de ejes. ¿Dónde se cruzan?
¿Cuál es la ecuación que describe el$x$ eje -eje?
¿Cuál es la ecuación que describe el$y$ eje -eje?

Responder

Captura de pantalla (516) .png — Figura$\PageIndex{27}$

Captura de pantalla (517) .png — Figura$\PageIndex{28}$

Captura (518) .png — Figura$\PageIndex{29}$

Captura de pantalla (519) .png — Figura$\PageIndex{30}$

Captura de pantalla (520) .png — Figura$\PageIndex{31}$

11. $y=0$

Ejercicio$\PageIndex{11}$ Mixed Practice

Gráfica trazando puntos.

$y=−\frac{3}{5}x+6$
$y=\frac{3}{5}x−3$
$y=−3$
$x=−5$
$3x−2y=6$
$−2x+3y=−12$

Responder

Captura de pantalla (521) .png — Figura$\PageIndex{32}$

Captura de pantalla (522) .png — Figura$\PageIndex{33}$

Captura de pantalla (523) .png — Figura$\PageIndex{34}$

Ejercicio$\PageIndex{12}$ Discussion Board Topics

Discutir la importancia de la relación entre álgebra y geometría en la descripción de líneas.
Dar ejemplos del mundo real relacionados con dos incógnitas

Responder: 1. Las respuestas pueden variar

Search

Text Color

Text Size

Margin Size

Font Type