6.3: Factorización de Trinomios de la Forma ax²+bx+c
- Page ID
- 110064
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Trinomios factoriales de la forma\(ax^{2}+bx+c\).
- Trinomios factoriales con un factor común.
Factorización de Trinomios de la Forma\(ax^{2}+bx+c\)
Factorizar trinomios de la forma\(ax^{2}+bx+c\) puede ser un desafío porque el término medio se ve afectado por los factores de ambos\(a\) y\(c\). Para ilustrar esto, considere el siguiente trinomio factorizado:
\(10x^{2}+17x+3=(2x+3)(5x+1)\)
Podemos multiplicar para verificar que esta es la factorización correcta.
\(\begin{aligned} (2x+3)(5x+1)&=10x^{2}+2x+15x+3 \\ &=10x^{2}+17x+3\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Como hemos visto antes, el producto de los primeros términos de cada binomio es igual al primer término del trinomio. El término medio del trinomio es la suma de los productos de los términos externo e interno de los binomios. El producto de los últimos términos de cada binomio es igual al último término del trinomio. Visualmente, tenemos lo siguiente:
.png)
En general,
\(\begin{aligned} \color{Cerulean}{a}\color{black}{x^{2}+}\color{Cerulean}{b}\color{black}{x+}\color{Cerulean}{c}&= (px+m)(qx+n) \\ &=pqx^{2}+pnx+qmx+mn \\ &=\color{Cerulean}{pq}\color{black}{x^{2}+}\color{Cerulean}{(pn+qm)}\color{black}{x+}\color{Cerulean}{mn} \end{aligned}\)
Esto nos da,
\[a=pq\quad\text{and}\quad b=pn+qm,\quad\text{where}\quad c=mn\]
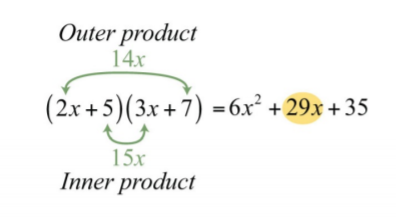
En definitiva, cuando el coeficiente principal de un trinomio es algo distinto a\(1\), habrá más a considerar a la hora de determinar los factores utilizando el método de ensayo y error. La clave radica en la comprensión de cómo se obtiene el término medio. Multiplicar\((2x+5)(3x+7)\) y seguir cuidadosamente la formación del término medio.
\(\begin{array}{ccc} {(\color{Cerulean}{2x}\color{black}{+}\color{OliveGreen}{5}\color{black}{)(3x+7)=\color{Cerulean}{2x}\color{black}{\cdot 3x}}}&{\underbrace{+\color{Cerulean}{2x}\color{black}{\cdot 7+}\color{OliveGreen}{5}\color{black}{\cdot 3x}}}&{+\color{OliveGreen}{5}\color{black}{\cdot 7}} \\ {}&{\color{Cerulean}{middle\:term}}&{} \end{array}\)
\(\begin{aligned} &=6x^{2}+14x+15x+35 \\ &=6x^{2}+29x+35 \end{aligned}\)
Si pensamos en el método FOIL para multiplicar binomios, entonces el término medio resulta de la suma del producto interno y el producto externo. En este caso\(14x+15x=29x\), como se ilustra a continuación:
.png)
Por ello, necesitamos buscar productos de los factores del primer y último término cuya suma sea igual al coeficiente del término medio. Por ejemplo, para factorizar\(6x^{2}+29x+35\), mirar los factores de\(6\) y\(35\).
\(\begin{array}{ccc}{6=1\cdot 6}&{\quad}&{35=1\cdot 35}\\{=\color{OliveGreen}{2\cdot 3}}&{\quad}&{=\color{OliveGreen}{5\cdot 7}} \end{array}\)
La combinación que produce el coeficiente del término medio es\(2⋅7+3⋅5=14+15=29\). Asegúrese de que los términos externos tengan coeficientes\(2\) y\(7\), y que los términos internos tengan coeficientes\(5\) y\(3\). Utilice esta información para factorizar el trinomio:
\(\begin{aligned} 6x^{2}+29x+35&=(2x\quad\color{Cerulean}{?}\color{black}{)(3x}\quad\color{Cerulean}{?}\color{black}{)} \\ &=(2x+5)(3x+7) \end{aligned}\)
Ejemplo\(\PageIndex{1}\)
Factor:
\(3x^{2}+7x+2\).
Solución:
Dado que el coeficiente principal y el último término son ambos primos, solo hay una manera de factorizar cada uno.
\(3=1\cdot 3\quad\text{and}\quad 2=1\cdot 2\)
Comience por escribir los factores del primer término,\(3x^{2}\), de la siguiente manera:
\(3x^{2}+7x+2=(x\quad\color{Cerulean}{?}\color{black}{)(3x}\quad\color{Cerulean}{?}\color{black}{)}\)
El término medio y último son ambos positivos; por lo tanto, los factores de\(2\) se eligen como números positivos. En este caso, la única opción es en qué agrupación colocar estos factores.
\((x+1)(3x+2)\quad\text{or}\quad (x+2)(3x+1)\)
Determine qué agrupación es correcta multiplicando cada expresión.
\(\begin{aligned} (x+1)(3x+2)&=3x^{2}+2x+3x+2 \\ &=3x^{2}+5x+2\quad\color{red}{x}\\(x+2)(3x+1)&=3x^{2}+x+6x+2 \\ &=3x^{2}+7x+2\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Observe que estos productos difieren solo en sus términos medios. Además, observe que el término medio es la suma del producto interno y externo, como se ilustra a continuación:
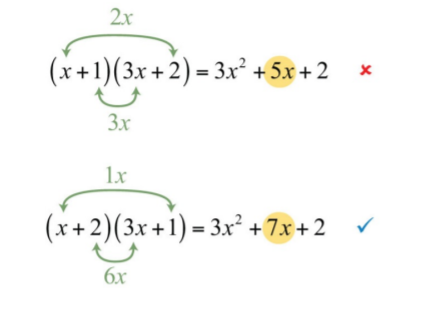.png)
Respuesta:
\((x+2)(3x+1)\)
Ejemplo\(\PageIndex{2}\)
Factor:
\(12x^{2}+38x+20\).
Solución:
Primero, considere los factores del primer y último término.
\(\begin{array}{ccc}{12=1\cdot 12}&{\quad}&{20=1\cdot 20}\\{=2\cdot 6}&{\quad}&{=2\cdot 10}\\{=3\cdot 4}&{\quad}&{=4\cdot 5} \end{array}\)
Buscamos productos de factores cuya suma sea igual al coeficiente del término medio,\(38\). Por brevedad, el proceso de pensamiento se ilustra a partir de los factores\(2\) y\(6\). El factoraje comienza en este punto con el primer término.
\(12x^{2}+38x+20=(2x\quad\color{Cerulean}{?}\color{black}{)(6x}\quad\color{Cerulean}{?}\color{black}{)}\)
Buscamos factores de 20 que junto con los factores de 12 producen un término medio de 38x
\(\begin{array}{lll} {Factors\:of\:20}&{Possible}&{factorization}\\{\color{Cerulean}{1\cdot 20}}&{(2x+1)(6x+20)}&{\color{Cerulean}{middle\:term\Rightarrow 46x}}\\{\color{Cerulean}{1\cdot 20}}&{(2x+20)(6x+1)}&{\color{Cerulean}{middle\:term\Rightarrow 122x}}\\{\color{Cerulean}{2\cdot 10}}&{(2x+2)(6x+10)}&{\color{Cerulean}{middle\:term\Rightarrow 32x}}\\{\color{Cerulean}{2\cdot 10}}&{(2x+10)(6x+2)}&{\color{Cerulean}{middle\:term\Rightarrow 64x}}\\{\color{Cerulean}{4\cdot 5}}&{(2x+4)(6x+5)}&{\color{Cerulean}{middle\:term\Rightarrow 34x}}\\{\color{Cerulean}{4\cdot 5}}&{\color{OliveGreen}{(2x+5)(6x+4)}}&{\color{OliveGreen}{middle\:term\Rightarrow 38x}\quad\color{Cerulean}{\checkmark}} \end{array}\)
Aquí la última combinación produce un término medio de\(38x\).
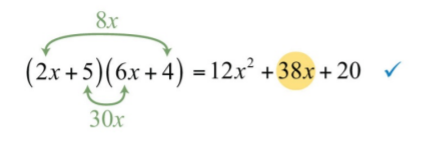.png)
Respuesta:
\((2x+5)(6x+4)\)
Ejemplo\(\PageIndex{3}\)
Factor:
\(10x^{2}−23x+6\).
Solución
Primero, considere los factores del primer y último término.
\(\begin{array}{ccc}{10=1\cdot 10}&{\quad}&{6=1\cdot 6}\\{=2\cdot 5}&{\quad}&{=2\cdot 3} \end{array}\)
Estamos buscando productos de factores cuya suma sea igual al coeficiente del término medio,\(−23\). La factorización comienza en este punto con dos conjuntos de paréntesis en blanco:
\(10x^{2}-23x+6=(\quad )(\quad )\)
Dado que el último término es positivo y el término medio es negativo, sabemos que ambos factores del último término deben ser negativos. Aquí enumeramos todas las combinaciones posibles con los factores de\(10x^{2}=2x⋅5x\).
\(10x^{2}-23x+6=(2x\quad\color{Cerulean}{?}\color{black}{)(5x}\quad\color{Cerulean}{?}\color{black}{)}\)
\(\begin{array}{ll}{(2x-1)(5x-6)}&{\color{Cerulean}{middle\:term\Rightarrow -17x}}\\{(2x-6)(5x-1)}&{\color{Cerulean}{middle\:term\Rightarrow -32x}}\\{(2x-2)(5x-3)}&{\color{Cerulean}{middle\:term\Rightarrow -16x}}\\{(2x-3)(5x-2)}&{\color{Cerulean}{middle\:term\Rightarrow -19x}} \end{array}\)
No hay ninguna combinación que produzca un término medio de\(−23x\). Luego pasamos a los factores de\(10x^{2}=10x⋅x\) y enumeramos todas las combinaciones posibles:
\(10x^{2}-23x+6=(10x\quad\color{Cerulean}{?}\color{black}{)(x}\quad\color{Cerulean}{?}\color{black}{)}\)
\(\begin{array}{ll}{(10x-1)(x-6)}&{\color{Cerulean}{middle\:term\Rightarrow -61x}}\\{(10x-6)(x-1)}&{\color{Cerulean}{middle\:term\Rightarrow -162x}}\\{(10x-2)(x-3)}&{\color{Cerulean}{middle\:term\Rightarrow -32x}}\\{\color{OliveGreen}{(10x-3)(x-2)}}&{\color{OliveGreen}{middle\:term\Rightarrow -23x}\quad\color{Cerulean}{\checkmark}} \end{array}\)
Y podemos escribir
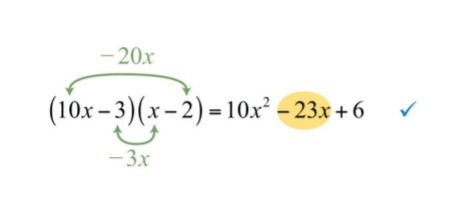.png)
Respuesta:
\((10x-3)(x-2)\). La comprobación completa se deja al lector.
Podemos reducir gran parte de las conjeturas que implica factorizar trinomios si consideramos todos los factores del primer y último término y sus productos.
Ejemplo\(\PageIndex{4}\)
Factor:
\(5x^{2}+38x-16\).
Solución:
Comenzamos con los factores de\(5\) y\(16\).
\(\begin{array}{cc}{}&{16=1\cdot 16}\\{5=1\cdot 5}&{=2\cdot 8}\\{}&{=4\cdot 4} \end{array}\)
Dado que el coeficiente principal es primo, podemos comenzar con lo siguiente:
\(5x^{2}+38x-16=(x\quad\color{Cerulean}{?}\color{black}{)(5x}\quad\color{Cerulean}{?}\color{black}{)}\)
Buscamos productos de los factores de 5 y 16 que posiblemente podrían sumar a 38.
\(\begin{array}{lll}{Factors\:of\:16}&{Possible}&{products}\\{\color{Cerulean}{1\cdot 16}}&{1\cdot\color{Cerulean}{1}\:\color{black}{and\: 5}\cdot\color{Cerulean}{16}}&{\color{Cerulean}{products\Rightarrow\:1\:and\:80}}\\{\color{Cerulean}{1\cdot 16}}&{1\cdot \color{Cerulean}{16}\:\color{black}{and\:5}\cdot\color{Cerulean}{1}}&{\color{Cerulean}{products\Rightarrow\:16\:and\:5}}\\{\color{Cerulean}{2\cdot 8}}&{1\cdot\color{Cerulean}{2}\:\color{black}{and\:5}\cdot\color{Cerulean}{8}}&{\color{OliveGreen}{products\Rightarrow\:2\:and\:40}\quad\color{Cerulean}{\checkmark}}\\{\color{Cerulean}{2\cdot 8}}&{1\cdot\color{Cerulean}{8}\:\color{black}{and\:5}\cdot\color{Cerulean}{2}}&{\color{Cerulean}{products\Rightarrow\:8\:and\:10}}\\{\color{Cerulean}{4\cdot 4}}&{1\cdot\color{Cerulean}{4}\:\color{black}{and\:5}\cdot\color{Cerulean}{4}}&{\color{Cerulean}{products\Rightarrow\:4\:and\:20}} \end{array}\)
Dado que el último término es negativo, debemos buscar factores con signos opuestos. Aquí podemos ver que los productos 2 y 40 suman 38 si tienen signos opuestos:
\(1\cdot (\color{Cerulean}{-2}\color{black}{)+5\cdot}\color{Cerulean}{8}\color{black}{=-2+40=38}\)
Por lo tanto, utilice\(−2\) y\(8\) como los factores de\(16\), asegurándose de que los productos internos y externos son\(−2x\) y\(40x\):
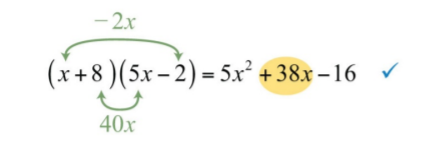.png)
Respuesta:
\((x+8)(5x-2)\). La comprobación completa se deja al lector.
Después de mucha práctica, el proceso descrito en el ejemplo anterior se puede realizar mentalmente.
Ejercicio\(\PageIndex{1}\)
Factor:
\(12x^{2}-31x-30\)
- Responder
-
\((3x-10)(4x+3)\)
Cuando se dan trinomios con múltiples variables, el proceso es similar.
Ejemplo\(\PageIndex{5}\)
Factor:
\(9x^{2}+30xy+25y^{2}\).
Solución:
Buscar factores del primer y último término tales que la suma de los productos internos y externos iguale al término medio.
\(\begin{array}{cc}{9x^{2}=1x\cdot 9x}&{25y^{2}=1y\cdot 25y}\\{=3x\cdot 3x}&{=5y\cdot 5y} \end{array}\)
Agregar los siguientes productos para obtener el término medio:\(3x⋅5y+3x⋅5y=30xy\).
\(\begin{aligned} 9x^{2}+30xy+25y^{2}&=(3x\quad )(3x\quad ) \\ &=(3x+5y)(3x+5y) \\ &=(3x+5y)^{2} \end{aligned}\)
En este ejemplo, tenemos un trinomio cuadrado perfecto. Cheque.
\(\begin{aligned} (3x+5y)^{2}&= 9x^{2}+2\cdot 3x\cdot 5y+25y^{2} \\ &=9x^{2}+30xy+25y^{2}\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Respuesta:
\((3x+5y)^{2}\)
Ejercicio\(\PageIndex{2}\)
Factor:
\(16x^{2}−24xy+9y^{2}\).
- Responder
-
\((4x-3y)^{2}\)
Factorización de Trinomios con Factores Comunes
Es una buena práctica factorizar primero el GCF, si lo hay. Hacer esto produce un factor trinomial con coeficientes más pequeños. Como hemos visto, los trinomios con coeficientes menores requieren mucho menos esfuerzo para factorizar. Este paso que comúnmente se pasa por alto merece la pena identificarlo temprano.
Ejemplo\(\PageIndex{6}\)
Factor:
\(12x^{2}-27x+6\).
Solución:
Comience por factorizar el GCF.
\(12x^{2}-27x+6=3(4x^{2}-9x+2)\)
Después de factorizar 3, los coeficientes del trinomio resultante son menores y tienen menos factores.
\(\begin{array}{cc}{4=\color{OliveGreen}{1\cdot 4}}&{2=\color{OliveGreen}{1\cdot 2}}\\{=2\cdot 2}&{}\end{array}\)
Después de pensarlo, podemos ver que la combinación que da el coeficiente del término medio es\(4(−2)+1(−1)=−8−1=−9\).
\(\begin{aligned}3(4x^{2}-9x+2)&=3(4x\quad\color{Cerulean}{?}\color{black}{)(x}\quad\color{Cerulean}{?}\color{black}{)} \\ &=3(4x-1)(x-2) \end{aligned}\)
Cheque.
\(\begin{aligned} 3(4x-1)(x-2)&=3(4x^{2}-8x-x+2) \\ &=3(4x^{2}-9x+2) \\ &=12x^{2}-27x+6\quad\color{Cerulean}{\checkmark} \end{aligned}\)
El factor\(3\) es parte de la forma factorizada de la expresión original; asegúrese de incluirla en la respuesta.
Respuesta:
\(3(4x-1)(x-2)\)
Es una buena práctica trabajar consistentemente con trinomios donde el coeficiente principal es positivo.
Ejemplo\(\PageIndex{7}\)
Factor:
\(−x^{2}+2x+15\).
Solución
En este ejemplo, el coeficiente principal es\(−1\). Antes de comenzar el proceso de factorización, factorizar\(−1\):
\(-x^{2}+2x+15=-1(x^{2}-2x-15)\)
En este punto, factoriza el trinomio restante como de costumbre, recordando escribir el\(−1\) como factor en tu respuesta final. Porque\(3 + (−5) = −2\), uso\(3\) y\(5\) como los factores de\(15\).
\(\begin{aligned} -x^{2}+2x=15&=-1(x^{2}-2x-15) \\ &=-1(x\quad )(x\quad )\\ &=-(x+3)(x-5) \end{aligned}\)
Respuesta:
\(-1(x+3)(x-5)\). El cheque se deja al lector.
Ejemplo\(\PageIndex{8}\)
Factor:
\(-60a^{2}-5a+30\)
Solución
El GCF de todos los términos es\(5\). Sin embargo, en este caso factorizar\(−5\) porque esto produce un factor trinomial donde el coeficiente principal es positivo.
\(-60a^{2}-5a+30=-5(12a^{2}+a-6)\)
Centrarse en los factores de\(12\) y\(6\) que se combinan para dar el coeficiente medio,\(1\).
\(\begin{array}{cc}{12=1\cdot 12}&{6=1\cdot 6}\\{=2\cdot 6}&{=\color{OliveGreen}{2\cdot 3}}\\{=\color{OliveGreen}{3\cdot 4}}&{} \end{array}\)
Después de pensarlo mucho, nos encontramos con eso\(3⋅3−4⋅2=9−8=1\). Factorizar el trinomio restante.
\(\begin{aligned} -60a^{2}-5a+30&=-5(12a^{2}+a-6) \\ &=-5(4a\quad )(3a\quad )\\&=-5(4a+3)(3a-2) \end{aligned}\)
Respuesta:
\(-5(4a+3)(3a-2)\). El cheque se deja al lector.
Ejercicio\(\PageIndex{3}\)
Factor:
\(24+2x−x^{2}\).
- Responder
-
\(−1(x−6)(x+4)\)
Factorización mediante el método de CA
En esta sección, factorizamos trinomios de la forma\(ax^{2}+bx+c\) utilizando el método AC descrito anteriormente.
Ejemplo\(\PageIndex{9}\)
Factor usando el método AC:
\(18x^{2}−21x+5\).
Solución:
Aquí\(a = 18, b = −21\), y\(c = 5\).
\(\begin{aligned}ac&=18(5) \\ &=90 \end{aligned}\)
Factorizar\(90\) y buscar factores cuya suma sea\(−21\).
\(\begin{aligned} 90&=1(90) \\ &=2(45) \\ &=3(30) \\ &=5(18) \\ &=\color{OliveGreen}{6(15)}\quad\color{Cerulean}{\checkmark} \\ &=9(10) \end{aligned}\)
En este caso, la suma de los factores\(−6\) y\(−15\) es igual al coeficiente medio,\(−21\). Por lo tanto\(−21x=−6x−15x\),, y podemos escribir
\(18x^{2}\color{OliveGreen}{-21x}\color{black}{+5=18x^{2}}\color{OliveGreen}{-6x-15x}\color{black}{+5}\)
Factorizar la expresión equivalente por agrupación.
\(\begin{aligned} 18x^{2}-21x+5&=18x^{2}-6x-15x+5 \\ &=6x(3x-1)-5(3x-1) \\ &=(3x-1)(6x-5) \end{aligned}\)
Respuesta:
\((3x-1)(6x-5)\)
Ejemplo\(\PageIndex{10}\)
Factor usando el método AC:\(9x^{2}−61x−14\).
Solución:
Aquí\(a = 9, b = −61\), y\(c = −14\).
Factorizamos de\(-126\) la siguiente manera:
\(\begin{aligned} -126&=1(-126) \\ &=\color{OliveGreen}{2(-63)}\quad\color{Cerulean}{\checkmark} \\ &=3(-42)\\&=6(-21)\\&=7(-18)\\&=9(-14) \end{aligned}\)
La suma de factores\(2\) y\(−63\) es igual al coeficiente medio,\(−61\). Reemplazar\(−61x\) con\(2x−63x\):
\(\begin{aligned} 9x^{2}-61x-14&=9x^{2}+2x-63x-14\quad\color{Cerulean}{Rearrange\:the\:terms.} \\ &=9x^{2}-63x+2x-14\quad\color{Cerulean}{Factor\:by\:grouping.}\\&=9x(x-7)+2(x-7) \\ &=(x-7)(9x+2) \end{aligned}\)
Respuesta:
\((x-7)(9x+2)\). El cheque se deja al lector.
Claves para llevar
- Si un trinomio de la forma\(ax^{2}+bx+c\) factores en el producto de dos binomios, entonces el coeficiente del término medio será la suma de ciertos productos de factores del primer y último término.
- Si el trinomio tiene un mayor factor común, entonces es una mejor práctica factorizar primero el GCF antes de intentar factorizarlo en un producto de binomios.
- Si el coeficiente principal de un trinomio es negativo, entonces es una buena práctica factorizar ese factor negativo antes de intentar factorizar el trinomio.
- Factorizar trinomios de la forma\(ax^{2}+bx+c\) requiere mucha práctica y paciencia. Es extremadamente importante tomarse el tiempo para dominar trabajando muchos ejercicios.
Ejercicio\(\PageIndex{4}\) Factoring Trinomials
Factor.
- \(3x^{2}−14x−5\)
- \(5x^{2}+7x+2 \)
- \(2x^{2}+5x−3 \)
- \(2x^{2}+13x−7 \)
- \(2x^{2}+9x−5 \)
- \(7x^{2}+20x−3 \)
- \(7x^{2}−46x−21 \)
- \(3x^{2}+x−2 \)
- \(5x^{2}+34x−7 \)
- \(5x^{2}−28x−12 \)
- \(9x^{2}−12x+4 \)
- \(4x^{2}−20x+25 \)
- \(49x^{2}+14x+1 \)
- \(25x^{2}−10x+1 \)
- \(2x^{2}+7x+16 \)
- \(6x^{2}−19x−10 \)
- \(27x^{2}+66x−16 \)
- \(12x^{2}−88x−15 \)
- \(12y^{2}−8y+1 \)
- \(16y^{2}−66y−27 \)
- \(9x^{2}−12xy+4y^{2} \)
- \(25x^{2}+40x+16 \)
- \(15x^{2}−26xy+8y^{2} \)
- \(12a^{2}−4ab−5b^{2} \)
- \(4x^{2}y^{2}+16xy−9 \)
- \(20x^{2}y^{2}+4xy−7 \)
- El área de un rectángulo viene dada por la función\(A(x)=3x^{2}−10x+3\), donde\(x\) se mide en metros. Reescribe esta función en forma factorizada.
- El área de un rectángulo viene dada por la función\(A(x)=10x^{2}−59x−6\), donde\(x\) se mide en metros. Reescribe esta función en forma factorizada.
- Responder
-
1. \((x−5)(3x+1) \)
3. \((x+3)(2x−1) \)
5. \((x+5)(2x−1) \)
7. \((x−7)(7x+3) \)
9. \((x+7)(5x−1) \)
11. \((3x−2)^{2}\)
13. \((7x+1)^{2} \)
15. Prime
17. \((3x+8)(9x−2)\)
19. \((6y−1)(2y−1) \)
21. \((3x−2y)^{2}\)
23. \((3x−4y)(5x−2y) \)
25. \((2xy−1)(2xy+9) \)
27. \(A(x)=(3x−1)(x−3)\)
Ejercicio\(\PageIndex{5}\) Factoring Trinomials with Common Factors
Factor.
- \(6x^{2}−20x−16 \)
- \(45x^{2}+27x−18 \)
- \(20x^{2}−20x+5 \)
- \(3x^{2}+39x−90 \)
- \(16x^{2}+26x−10 \)
- \(54x^{2}−15x+6 \)
- \(45x^{2}−45x−20 \)
- \(90x^{2}+300x+250 \)
- \(40x^{2}−36xy+8y^{2} \)
- \(24a^{2}b^{2}+18ab−81 \)
- \(6x^{2}y^{2}+46xy+28 \)
- \(2x^{5}+44x^{4}+144x^{3}\)
- \(5x^{3}−65x^{2}+60x\)
- \(15a^{4}b^{2}−25a^{3}b−10a^{2}\)
- \(6a^{4}b+2a^{3}b^{2}−4a^{2}b^{3}\)
- \(20a^{3}b^{2}−60a^{2}b^{3}+45ab^{4}\)
- Responder
-
1. \(2(x−4)(3x+2) \)
3. \(5(2x−1)^{2}\)
5. \(2(8x^{2}+13x−5) \)
7. \(5(3x−4)(3x+1) \)
9. \(4(5x−2y)(2x−y) \)
11. \(2(xy+7)(3xy+2) \)
13. \(5x(x−12)(x−1) \)
15. \(2a^{2}b(3a−2b)(a+b)\)
Ejercicio\(\PageIndex{6}\) Factoring Trinomials with Common Factors
Factor hacia fuera\(−1\) y luego factorizar más.
- \(−x^{2}−4x+21 \)
- \(−x^{2}+x+12 \)
- \(−x^{2}+15x−56 \)
- \(−x^{2}+x+72 \)
- \(−y^{2}+10y−25 \)
- \(−y^{2}−16y−64 \)
- \(36−9a−a^{2} \)
- \(72−6a−a^{2}\)
- \(32+4x−x^{2}\)
- \(200+10x−x^{2}\)
- Responder
-
1. \(−1(x−3)(x+7) \)
3. \(−1(x−7)(x−8) \)
5. \(−1(y−5)^{2}\)
7. \(−1(a−3)(a+12) \)
9. \(−1(x−8)(x+4)\)
Ejercicio\(\PageIndex{7}\) Factoring Trinomials with Common Factors
Primero factorizar un factor común negativo y luego factorizar más si es posible.
- \(−8x^{2}+6x+9 \)
- \(−4x^{2}+28x−49 \)
- \(−18x^{2}−6x+4 \)
- \(2+4x−30x^{2} \)
- \(15+39x−18x^{2} \)
- \(90+45x−10x^{2} \)
- \(−2x^{2}+26x+28 \)
- \(−18x^{3}−51x^{2}+9x \)
- \(−3x^{2}y^{2}+18xy^{2}−24y^{2} \)
- \(−16a^{4}+16a^{3}b−4a^{2}b^{2} \)
- La altura en pies de un proyectil lanzado desde una torre viene dada por la función\(h(t)=−16t^{2}+64t+80\), donde\(t\) representa el número de segundos después del lanzamiento. Reescribe la función dada en forma factorizada.
- La altura en pies de un proyectil lanzado desde una torre viene dada por la función\(h(t)=−16t^{2}+64t+192\), donde\(t\) representa el número de segundos después del lanzamiento. Reescribe la función dada en forma factorizada.
- Responder
-
1. \(−(2x−3)(4x+3) \)
3. \(−2(3x−1)(3x+2) \)
5. \(−3(2x−5)(3x+1) \)
7. \(−2(x−14)(x+1) \)
9. \(−3y^{2}(x−4)(x−2) \)
11. \(h(t)=−16(t+1)(t−5) \)
Ejercicio\(\PageIndex{8}\) Factoring Using the AC Method
Factor usando el método AC.
- \(2x^{2}+5x−7 \)
- \(3x^{2}+7x−10 \)
- \(4x^{2}−25x+6 \)
- \(16x^{2}−38x−5 \)
- \(6x^{2}+23x−18 \)
- \(8x^{2}+10x−25 \)
- \(4x^{2}+28x+40 \)
- \(−6x^{2}−3x+30 \)
- \(12x^{2}−56xy+60y^{2}\)
- \(20x^{2}+80xy+35y^{2}\)
- Responder
-
1. \((x−1)(2x+7) \)
3. \((x−6)(4x−1) \)
5. \((2x+9)(3x−2) \)
7. \(4(x+2)(x+5) \)
9. \(4(x−3y)(3x−5y)\)
Ejercicio\(\PageIndex{9}\) Discussion Board Topics
- Crea tu propio trinomio de la forma\(ax^{2}+bx+c\) que factoriza. Compártelo, junto con la solución, en el panel de discusión.
- Escribe tu propia lista de pasos para factorizar un trinomio del formulario\(ax^{2}+bx+c\) y compártelo en el tablero de discusión.
- Crear un trinomio de la forma\(ax^{2}+bx+c\) que no factoriza y compartirlo junto con la razón por la que no factoriza.
- Responder
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar


