6.4: Factorización de binomios especiales
- Page ID
- 110057
Objetivos de aprendizaje
- Binomios factoriales que son diferencias de cuadrados.
- Binomios de factores que son sumas y diferencias de cubos.
Diferencia de Cuadrados
Un binomio es un polinomio con dos términos. Comenzamos con nuestro primer binomio especial llamado diferencia de cuadrados:
\[a^{2}-b^{2}=(a+b)(a-b)\]
Para verificar la fórmula anterior, multiplique:
\(\begin{aligned} (a+b)(a-b)&=a^{2}-ab+ba-b^{2} \\&=a^{2}\color{red}{-ab+ab}\color{black}{-b^{2}} \\ &=a^{2}-b^{2} \end{aligned}\)
Utilizamos esta fórmula para factorizar ciertos binomios especiales.
Ejemplo\(\PageIndex{1}\)
Factor:
\(x^{2}-16\).
Solución:
Paso 1: Identificar el binomio como diferencia de cuadrados y determinar los factores cuadrados de cada término.
.png)
Aquí podemos escribir
\(x^{2}-16=(\color{Cerulean}{x}\color{black}{)^{2}-(}\color{Cerulean}{4}\color{black}{)^{2}}\)
Los términos son cuadrados de\(x\) y\(4\). De ahí\(a=x\) y\(b=4\).
Paso 2: Sustituir en la fórmula de diferencia de cuadrados.
\(\begin{aligned}a^{2}-b^{2}&=(a+b)(a-b) \\ &\:\:\color{Cerulean}{\:\quad\downarrow\quad\:\downarrow\quad\downarrow\quad\downarrow} \\ x^{2}-16&=(x+4)(x-4) \end{aligned}\)
Paso 3: Multiplicar para verificar. Este paso es opcional.
Respuesta:
\((x+4)(x-4)\)
Vale la pena tomarse un tiempo extra en este punto para revisar todos los cuadrados de enteros desde\(1\) hasta\(12\).
\(\begin{array}{ll}{1^{2}=1}&{7^{2}=49}\\{2^{2}=4}&{8^{2}=64}\\{3^{2}=9}&{9^{2}=81}\\{4^{2}=16}&{10^{2}=100}\\{5^{2}=25}&{11^{2}=121}\\{6^{2}=36}&{12^{2}=144} \end{array}\)
Reconocer estos enteros cuadrados perfectos ayuda a acelerar el proceso de factorización.
Ejemplo\(\PageIndex{2}\)
Factor:
\(9x^{2}-121\).
Solución:
La resta indica que esto es una diferencia. Además, reconocemos que los términos son cuadrados.
\(9x^{2}-121=(\color{Cerulean}{3x}\color{black}{)^{2}-(}\color{Cerulean}{11}\color{black}{)^{2}}\)
En este caso,\(a=3x\) y\(b=11\). Sustituir en la fórmula para diferencia de cuadrados.
\(\begin{aligned} a^{2}-b^{2}&=(a+b)(a-b) \\ 9x^{2}-121&=(3x+11)(3x-11) \end{aligned}\)
Respuesta:
\((3x+11)(3x-11)\)
Puede darse el caso de que los términos del binomio tengan un factor común. Si es así, será difícil identificar los cuadrados perfectos hasta que primero factorizamos el GCF.
Ejemplo\(\PageIndex{3}\)
Factor:
\(12y^{2}−75\).
Solución:
Los términos no son cuadrados perfectos. No obstante, observe que sí tienen un factor común. Primero, factorizar el GCF,\(3\).
\(12y^{2}-75=3(4y^{2}-25)\)
El factor binomial resultante es una diferencia de cuadrados con\(a=2y\) y\(b=5\).
\(\begin{aligned} 12y^{2}-75&=3(4y^{2}-25) \\ &=3(2y+5)(2y-5) \end{aligned}\)
Respuesta:
\(3(2y+5)(2y-5)\)
Ejemplo\(\PageIndex{4}\)
Factor:
\(49x^{2}−100y^{2}\).
Solución:
Aquí tenemos un binomio con dos variables y reconocemos que es una diferencia de cuadrados.
\(49x^{2}-100y^{2}=(\color{Cerulean}{7x}\color{black}{)^{2}-(}\color{Cerulean}{10y}\color{black}{)^{2}}\)
Por lo tanto,\(a=7x\) y\(b=10y\). Sustituir en la fórmula para diferencia de cuadrados.
\(\begin{aligned} a^{2}-b^{2}&=(a+b)(a-b) \\ 49x^{2}-100y^{2}&=(7x+10y)(7x-10y) \end{aligned}\)
Respuesta:
\((7x+10y)(7x-10y)\)
Ejercicio\(\PageIndex{1}\)
Factor:
\(36x^{2}−1\).
- Contestar
-
\((6x+1)(6x−1)\)
Dado cualquier número real\(b\), un polinomio de la forma\(x^{2}+b^{2}\) es primo.
Además, la suma de cuadrados\(a^{2}+b^{2}\) no tiene un equivalente factorizado general. Se debe tener cuidado de no confundir esto con un trinomio cuadrado perfecto:
\(\begin{aligned}(a+b)^{2}&=(a+b)(a+b) \\ &=a^{2}+ab+ba+b^{2} \\ &=a^{2}+2ab+b^{2} \end{aligned}\)
Por lo tanto,
\[(a+b)^{2}\neq a^{2}+b^{2}\]
Cuando el grado del binomio especial es mayor que dos, es posible que necesitemos aplicar la fórmula de diferencia de cuadrados múltiples veces. Un polinomio es completamente factorizado cuando ninguno de los factores puede ser factorizado más.
Ejemplo\(\PageIndex{5}\)
Factor completamente:
\(x^{4}−16\).
Solución:
Primero, identificar lo que se está poniendo al cuadrado:
\(x^{4}-16=(\quad )^{2}-(\quad )^{2}\)
Para ello, recordemos la regla de poder para los exponentes,\((x^{m})^{^{n}}=x^{m^{n}}\). Cuando los exponentes se elevan a una potencia, multiplicarlos. Con esto en mente, determine eso\((x^{2})^{^{2}}=x^{4}\) y escriba
\(x^{4}-16=(x^{2})^{^{2}}-(4)^{2}\)
Por lo tanto,\(a=x^{2}\) y\(b=4\). Sustituir en la fórmula para diferencia de cuadrados.
\(x^{4}-16=(x^{2}+4)(x^{2}-4)\)
En este punto, observe que el factor\((x^{2}−4)\) es en sí mismo una diferencia de dos cuadrados y así se puede factorizar aún más usando\(a=x\) y\(b=2\). El factor\((x^{2}+4)\) es una suma de cuadrados, que no se pueden factorizar usando números reales.
\(\begin{aligned} x^{4}-16&=(x^{2}+4)(x^{2}-4) \\ &=(x^{2}+4)(x+2)(x-2) \end{aligned}\)
Respuesta:
\((x^{2}+4)(x+2)(x-2)\)
Ejercicio\(\PageIndex{2}\)
Factor completamente:
\(81x^{4}−1\).
- Contestar
-
\((9x^{2}+1)(3x+1)(3x−1)\)
Suma y Diferencia de Cubos
Otros dos binomios especiales de interés son la suma y diferencia de cubos:
\[ a^{3}+b^{3}=(a+b)(a^{2}-ab+b^{2}) \]
\[ a^{3}-b^{3}=(a-b)(a^{2}+ab+b^{2}) \]
Podemos verificar estas fórmulas multiplicando:
\(\begin{aligned} (a+b)(a^{2}-ab+b^{2})&=a^{3}-a^{2}b+ab^{2}-ab^{2}+b^{3} \\ &=a^{3}+b^{3}\quad\color{Cerulean}{\checkmark} \\ (a-b)(a^{2}+ab+b^{2})&=a^{3}+a^{2}b+ab^{2}=a^{2}b-ab^{2}-b^{3} \\ &=a^{3}-b^{3}\quad\color{Cerulean}{\checkmark} \end{aligned}\)
El proceso para factorizar la suma y diferencia de cubos es muy similar al de la diferencia de cuadrados. Primero identificamos\(a\)\(b\) y luego sustituimos en la fórmula apropiada. Las fórmulas separadas para suma y diferencia de cubos nos permiten elegir siempre\(a\) y\(b\) ser positivos.
Ejemplo\(\PageIndex{6}\)
Factor:
\(x^{3}+8\).
Solución:
El signo más y el hecho de que los términos sean cubos nos indican que se trata de una suma de cubos.
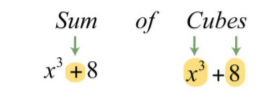.png)
A continuación, identificar lo que se está recogiendo en cubos.
\(x^{3}+8=(\color{Cerulean}{x}\color{black}{)^{3}+(}\color{Cerulean}{2}\color{black}{)^{3}}\)
En este caso,\(a=x\) y\(b=2\). Sustituir en la fórmula de suma de cubos.
\(\begin{aligned} a^{3}+b^{3}&=(a+b)(a^{2}-a\:\:b+\:\:b^{2}) \\ &\color{Cerulean}{\:\:\quad\downarrow\:\:\quad\downarrow\quad\downarrow\:\:\quad\downarrow\:\:\:\downarrow\quad\:\:\downarrow} \\ x^{3}+8&=(x+2)(x^{2}-x\cdot 2+2^{2}) \\ &=(x+2)(x^{2}-2x+4) \end{aligned}\)
El trinomio resultante es primo y la factorización es completa. Podemos comprobar esta factorización multiplicando.
\(\begin{aligned} (x+2)(x^{2}-2x+4)&= x^{3}-2x^{2}+4x+2x^{2}-4x+8 \\ &=x^{3} -\color{Cerulean}{\cancel{\color{black}{2x^{2}}}}\color{black}{+}\color{Cerulean}{\cancel{\color{black}{4x}}}\color{black}{+}\color{Cerulean}{\cancel{\color{black}{2x^{2}}}}\color{black}{-}\color{Cerulean}{\cancel{\color{black}{4x}}}\color{black}{+8} \\ &=x^{3}+8\quad\color{Cerulean}{\checkmark} \end{aligned}\)
Respuesta:
\((x-2)(x^{2}-2x+4)\)
Es útil revisar los cubos perfectos de enteros desde\(1\) hasta\(12\). Esto te ayudará a identificar sumas y diferencias de cubos.
\(\begin{array}{ll} {1^{3}=1}&{y^{3}=343}\\{2^{3}=8}&{8^{3}=512}\\{3^{3}=27}&{9^{3}=729}\\{4^{3}=64}&{10^{3}=1000}\\{5^{3}=125}&{11^{3}=1331}\\{6^{3}=216}&{12^{3}=1728} \end{array}\)
Ejemplo\(\PageIndex{7}\)
Factor:
\(y^{3}-125\).
Solución:
En este caso, tenemos una diferencia de cubos.
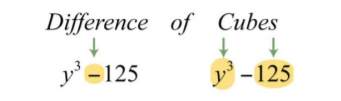.png)
Podemos escribir
\(y^{3}-125=(\color{Cerulean}{y}\color{black}{)^{3}-(}\color{Cerulean}{5}\color{black}{)^{3}}\)
Sustituir\(a=y\) y\(b=5\) en la fórmula para diferencia de cubos.
\(\begin{aligned} a^{3}-b^{3}&=(a-b)(a^{2}+a\:\:b+\:\:b^{2}) \\ &\color{Cerulean}{\:\:\quad\downarrow\:\:\quad\downarrow\quad\downarrow\:\:\quad\downarrow\:\:\:\downarrow\quad\:\:\downarrow} \\ y^{3}-1258&=(y-5)(y^{2}+y\cdot 5+5^{2}) \\ &=(y-5)(y^{2}+5y+25) \end{aligned}\)
Respuesta:
\((y-5)(y^{2}+5y+25)\)
Siempre busque factores comunes a la hora de factorizar. Si los términos del binomio tienen un GCF distinto de\(1\), entonces factorizar eso primero.
Ejemplo\(\PageIndex{8}\)
Factor:
\(54x^{4}+128x\).
Solución:
Comience por factorizar el GCF\(2x\).
\(54x^{4}+128x=2x(27x^{3}+64)\)
El factor binomial resultante es una suma de cubos, donde\(a=3x\) y\(b=4\).
\(\begin{aligned} 54x^{4}+128x &=2x(27x^{3}+64) \\ &=2x(3x+4)((3x)^{2}-(3x)(4)+4^{2}) \\ &=2x(3x+4)(9x^{2}-12x+16) \end{aligned}\)
Respuesta:
\(2x(3x+4)(9x^{2}-12x+16)\)
Ejemplo\(\PageIndex{9}\)
Factor:
\(x^{3}y^{3}-1\).
Solución
Este binomio es una diferencia de cubos con dos variables. Identificar lo que se está cubicando.
\(x^{3}y^{3}-1=(\color{Cerulean}{xy}\color{black}{)^{3}-(}\color{Cerulean}{1}\color{black}{)^{3}}\)
Aquí\(a=xy\) y\(b=1\). Sustituir en la fórmula apropiada y simplificar.
\(\begin{aligned} a^{3}-b^{3}&=(a-b)(a^{2}+ab+b^{2}) \\ x^{3}y^{3}-1&=(xy-1)((xy)^{2}+xy\cdot 1+1^{2}) \\ &=(xy-1)(x^{2}y^{2}+xy+1) \end{aligned}\)
Respuesta:
\((xy-1)(x^{2}y^{2}+xy+1)\)
Ejercicio\(\PageIndex{3}\)
Factor:
\(8x^{3}+343\).
- Contestar
-
\((2x+7)(4x^{2}−14x+49)\)
Al factorizar, siempre busque los factores resultantes para factorizar aún más.
Ejemplo\(\PageIndex{10}\)
Factor completamente:
\(x^{6}−64\).
Solución:
Cuando se enfrenta a un binomio que es a la vez una diferencia de cuadrados y cubos, como esto es, hacer que sea una regla factorizar usando diferencia de cuadrados primero.
\(x^{6}-64=(\color{Cerulean}{x^{3}}\color{black}{)^{^{2}}-(}\color{Cerulean}{8}\color{black}{)^{2}}\)
Por lo tanto,\(a=x^{3}\) y\(b=8\). Sustituir en la fórmula de diferencia de cuadrados.
\(x^{6}-64=(x^{3}+8)(x^{3}-8)\)
Los dos factores binomiales resultantes son una suma y una diferencia de cubos. Cada uno se puede factorizar aún más.
\(\begin{aligned} x^{3}+8&=(x+2)(x^{2}-2x+2^{2}) \\ x^{3}-8&=(x-2)(x^{2}+2x+2^{2}) \end{aligned}\)
Por lo tanto, tenemos
\(\begin{array}{ccccc} {x^{6}-64}&{=}&{(x^{3}+8)}&{\cdot}&{(x^{3}-8)}\\{}&{=}&{\color{Cerulean}{\overbrace{\color{black}{(x+2)(x^{2}-2x+4)}}}}&{\cdot}&{\color{Cerulean}{\overbrace{\color{black}{(x-2)(x^{2}+2x+4)}}}} \end{array}\)
Los factores trinomiales son primos y la expresión está completamente factorizada.
Respuesta:
\((x+2)(x^{2}−2x+4)(x−2)(x^{2}+2x+4)\)
Como ejercicio, factorizar el ejemplo anterior como una diferencia de cubos primero y luego comparar los resultados. ¿Por qué crees que hacemos una regla factorizar primero usando diferencia de cuadrados?
Ejercicio\(\PageIndex{4}\)
Factor:
\(x^{6}−y^{6}\).
- Contestar
-
\((x+y)(x^{2}−xy+y2)(x−y)(x^{2}+xy+y2)\)
Claves para llevar
- Al factorizar binomios especiales, el primer paso es identificarlo como una suma o diferencia. Una vez que identificamos el binomio, entonces determinamos los valores de\(a\) y\(b\) y sustituimos en la fórmula apropiada.
- Se deben memorizar las fórmulas para todos los binomios especiales. Además, para ayudar a facilitar la identificación de binomios especiales, memorizar los cuadrados y cubos de enteros hasta por lo menos\(12\).
- Si un binomio es tanto una diferencia de cuadrados como de cubos, entonces primero factorizarlo como una diferencia de cuadrados.
Ejercicio\(\PageIndex{5}\) Difference of Squares
Factorizar completamente.
- \(x^{2}−9\)
- \(x^{2}−100 \)
- \(y^{2}−36 \)
- \(y^{2}−144 \)
- \(x^{2}+4 \)
- \(x^{2}−5 \)
- \(m^{2}−81 \)
- \(m^{2}−64 \)
- \(16x^{2}−9 \)
- \(25x^{2}−4 \)
- \(144x^{2}−1 \)
- \(9x^{2}−121 \)
- \(4y^{2}−81 \)
- \(100y^{2} −49 \)
- \(9 − 4 x^{2}\)
- \(100 −x^{2}\)
- \(1 −y^{2}\)
- \(25 − 9y^{2}\)
- \(− 3 x^{2} +75\)
- \(−16 x^{2} +25\)
- \(2 x^{2} −72\)
- \(20 x^{3} −45 x\)
- \(−48 x +27x^{3}\)
- \(36 x^{2} −100\)
- \(x^{2} −y^{2}\)
- \(25 x^{2} − 9y^{2}\)
- \(a^{2} − 4 b^{2}\)
- \(a^{2} b^{2} −36\)
- \(4 x^{2}y^{2} − 1\)
- \(x^{2}y^{2} −25\)
- \(2 a^{3} − 8ab^{2}\)
- \(3 a^{3} b^{4} −75ab^{2}\)
- \(−100xy^{3} + 4x^{3}y\)
- \(−18 x^{3}y^{3} +32xy\)
- \((x + 1 )^{2} −y^{2}\)
- \(x^{2}−(y − 2 )^{2}\)
- \((x − 3 )^{2}−(y + 3 )^{2}\)
- \((x^{2} + 2 )^{2}−(x − 1 )^{2}\)
- \((x^{2} − 1 )^{2}−( 2 x + 3 )^{2}\)
- \(x^{4} − 1\)
- \(x^{4} −y^{4}\)
- \(16 x^{4} −81\)
- \(a^{4}b^{4}−16\)
- \(a^{4}−16b^{4}\)
- \(x^{8}−1\)
- \(25x^{8}−1\)
- \(a^{8}−b^{2}\)
- \(a^{4}−9\)
- \(x^{8}−y^{8}\)
- \(81x^{8}−1 \)
- La altura de un proyectil caído desde una torre de\(64\) -pie viene dada por la función\(h(t)=−16t^{2}+64\), donde\(t\) representa el tiempo en segundos después de que es caído. Reescribe esta función en forma factorizada. (Pista: Factorizar\(−16\) primero.)
- La altura de un proyectil caído desde una torre de\(36\) -pie viene dada por la función\(h(t)=−16t^{2}+36\), donde\(t\) representa el tiempo en segundos después de que es caído. Reescribe esta función en forma factorizada.
- Contestar
-
1. \((x+3)(x−3) \)
3. \((y+6)(y−6) \)
5. Prime
7. \((m+9)(m−9) \)
9. \((4x+3)(4x−3) \)
11. \((12x+1)(12x−1) \)
13. \((2y+9)(2y−9) \)
15. \((3+2x)(3−2x) \)
17. \((1+y)(1−y) \)
19. \(−3(x+5)(x−5) \)
21. \(2(x+6)(x−6) \)
23. \(3x(3x+4)(3x−4) \)
25. \((x +y)(x −y ) \)
27. \(( a + 2 b)( a − 2 b ) \)
29. \(( 2xy + 1)( 2xy − 1 ) \)
31. \(2 a ( a + 2 b)( a − 2 b ) \)
33. \(4xy (x + 5y)(x − 5y ) \)
35. \((x + 1 +y)(x + 1 −y ) \)
37. \((x +y)(x −y − 6 ) \)
39. \((x^{2} + 2 x + 2)(x^{2} − 2 x − 4 ) \)
41. \((x^{2} +y^{2} ) (x +y)(x −y ) \)
43. \(( a^{2} b^{2} + 4 ) (ab + 2)(ab − 2 ) \)
45. \((x^{4} + 1)(x^{2} + 1 ) (x + 1)(x − 1 ) \)
47. \(( a^{4} + b)( a^{4} − b ) \)
49. \((x^{4} +y^{4})(x^{2} +y^{2} ) (x +y)(x −y )\)
51. \(h ( t)=−16 ( t + 2)( t − 2 )\)
Ejercicio\(\PageIndex{6}\) Sum and Difference of Cubes
Factorizar completamente.
- \(x^{3}−1 \)
- \(x^{3}+1 \)
- \(y^{3}−27 \)
- \(y^{3}−8 \)
- \(8y^{3}+1 \)
- \(27y^{3}−1 \)
- \(64a^{3}−125 \)
- \(8a^{3}+27 \)
- \(a^{3}+216 \)
- \(a^{3}−125 \)
- \(x^{3}−1000 \)
- \(343m^{3}−1 \)
- \(512 n^{3} + 1 \)
- \(8 x^{3} +343 \)
- \(40y^{3} −135 \)
- \(27y^{3} +729 \)
- \(27y^{3} −64 \)
- \(x^{3} + 3 \)
- \(5 x^{3} + 1\)
- \(1 −y^{3}\)
- \(27 −1,000y^{3}\)
- \(343 +125 a^{3}\)
- \(x^{3} −y^{3}\)
- \(x^{3} +y^{3}\)
- \(x^{3}y^{3} +125\)
- \(8 x^{3}y^{3} −27\)
- \(27 a^{3} − 8 b^{3}\)
- \(16 x^{3} −250y^{3}\)
- \(128 x^{3} + 2y^{3}\)
- \(54 x^{3} − 2y^{3}\)
- \(3 a^{4} b −24ab^{4}\)
- \(a^{3} b^{3} c^{3} − 1\)
- \((x + 1 )^{3} − 8\)
- \(8 x^{3}−(x − 5 )^{3}\)
- \((x − 2 )^{3}+(x + 2 )^{3}\)
- \(( a + 3 )^{3}+( b − 3 )^{3}\)
- \(x^{6} − 1\)
- \(x^{6} + 1\)
- \(64 a^{6} − 1\)
- \(a^{6} −81 b^{6}\)
- \(x^{6} −y^{6}\)
- \(x^{6}+y^{6}\)
- Contestar
-
1. \((x − 1 ) (x^{2} +x + 1 ) \)
3. \((y − 3 ) (y^{2} + 3 y + 9 ) \)
5. \(( 2y + 1 ) ( 4y^{2} − 2y + 1 ) \)
7. \(( 4 a − 5 ) (16 a^{2} +20 a +25 ) \)
9. \(( a + 6 ) ( a^{2} − 6 a +36 ) \)
11. \((x −10 ) (x^{2} +10 x +100 ) \)
13. \(( 8 n + 1 ) (64 n^{2} − 8 n + 1 ) \)
15. \(5 ( 2y − 3 ) ( 4y^{2} + 6y + 9 ) \)
17. \(( 3 y − 4 ) ( 9y^{2} +12y +16 ) \)
19. Prime
21. \(( 3 −10y ) ( 9 +30y +100y^{2} )\)
23. \((x −y ) (x^{2} +xy +y^{2} )\)
25. \((xy + 5 ) (x^{2}y^{2} − 5xy +25 ) \)
27. \(( 3 a − 2 b ) ( 9 a^{2} + 6ab + 4 b^{2} )\)
29. \(2 ( 4 x +y ) (16 x^{2} − 4xy +y^{2} )\)
31. \(3ab(a−2b)(a^{2}+2ab+4b^{2})\)
33. \((x−1)(x^{2}+4x+7) \)
35. \(2x(x^{2}+12) \)
37. \((x+1)(x^{2}−x+1)(x−1)(x^{2}+x+1) \)
39. \((2a+1)(4a^{2}−2a+1)(2a−1)(4a^{2}+2a+1) \)
41. \((x+y)(x^{2}−xy+y^{2})(x−y)(x^{2}+xy+y^{2})\)
Ejercicio\(\PageIndex{7}\) Discussion Board Topics
- Si un binomio cae en ambas categorías, diferencia de cuadrados y diferencia de cubos, cuál sería mejor factorizarlo como, y ¿por qué? Crear un ejemplo que ilustre esta situación y factorizarla usando ambas fórmulas.
- ¿Qué se puede decir de los grados de los factores de un polinomio? Dé un ejemplo.
- Haga su propio ejercicio de factorización de diferencia de cuadrados y brinde la respuesta. Explica cómo lo resolviste.
- Haga su propio ejercicio de factoraje de suma o diferencia de cubos y proporcione la respuesta. Explica cómo lo resolviste.
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar


