9.1: Extracción de Raíces Cuadradas

Objetivos de aprendizaje

• Resolver ecuaciones cuadráticas extrayendo raíces cuadradas.

Extracción de raíces cuadradas

Recordemos que una ecuación cuadrática está en forma estándar si es igual a 0:

\[a x^{2}+b x+c=0\]

donde a, b, y c son números reales y\(a\neq 0\). Una solución a tal ecuación se llama raíz. Las ecuaciones cuadráticas pueden tener dos soluciones reales, una solución real o ninguna solución real. Si la expresión cuadrática en los factores de la izquierda, entonces podemos resolverlo factorizando. Una revisión de los pasos utilizados para resolver mediante factorización sigue:

Paso 1: Exprese la ecuación cuadrática en forma estándar.

Paso 2: Factorizar la expresión cuadrática.

Paso 3: Aplicar la propiedad de cero producto y establecer cada factor variable igual a 0.

Paso 4: Resolver las ecuaciones lineales resultantes.

Por ejemplo, podemos resolver\(x^{2}-4=0\) factorizando de la siguiente manera:

\ (x+2) (x-2) &=0\\ x+2 &=0\ quad\ texto {o}\ cuádruple x-2=0\\ x &=-2\ cuádruple\ cuádruple\ cuádruple\ cuádruple\ :x=2\ final {alineado}\) </p">

Las dos soluciones son −2 y 2. El objetivo en esta sección es desarrollar un método alternativo que pueda ser utilizado para resolver fácilmente ecuaciones donde b = 0, dando la forma

\[a x^{2}+c=0\]

La ecuación\(x^{2}-4=0\) está en esta forma y puede resolverse aislando primero\(x^{2}\).

Si tomamos la raíz cuadrada de ambos lados de esta ecuación, obtenemos lo siguiente:

\(\begin{aligned} \sqrt{x^{2}} &=\sqrt{4} \\|x| &=2 \end{aligned}\)

Aquí vemos eso\(x=-2\) y\(x=2\) son soluciones a la ecuación resultante. En general, esto describe la propiedad de raíz cuadrada; para cualquier número real k,

\[\text{If}\:x^{2}=k, \text { then } x=\pm \sqrt{k}\]

La notación “±” se lee “más o menos” y se utiliza como notación compacta que indica dos soluciones. De ahí que el enunciado\(x=\pm \sqrt{k}\) indique que\(x= - \sqrt{k}\) o\(x= + \sqrt{k}\). Aplicar la propiedad de raíz cuadrada como medio para resolver una ecuación cuadrática se llama extraer las raíces.

Ejemplo\(\PageIndex{1}\)

Resolver:

\(x^{2}-25=0\)

Solución:

Comience aislando el cuadrado.

A continuación, aplicar la propiedad de raíz cuadrada.

\(\begin{aligned} x^{2} &=25 \\ x &=\pm \sqrt{25} \\ x &=\pm 5 \end{aligned}\)

Respuesta:

Las soluciones son −5 y 5. El cheque se deja al lector.

Ciertamente, el ejemplo anterior podría haberse resuelto con la misma facilidad factorizando. Sin embargo, demuestra una técnica que puede ser utilizada para resolver ecuaciones en esta forma que no factorizan.

Ejemplo\(\PageIndex{2}\)

Resolver:

\(x^{2}-5=0\)

Solución:

Observe que la expresión cuadrática de la izquierda no factoriza. Podemos extraer las raíces si primero aislamos el término principal,\(x^{2}\).

Aplicar la propiedad de raíz cuadrada.

\(x=\pm \sqrt{5}\)

Para la completitud, compruebe que estas dos soluciones reales resuelven la ecuación cuadrática original. Generalmente, el cheque es opcional.

\(\begin{array}{rlrl}{\text { Check } x=-\sqrt{5}} & {\text { Check } x=\sqrt{5}} \\ {x^{2}-5=0} & {x^{2}-5=0} \\ {(\color{OliveGreen}{-\sqrt{5}}\color{black}{)}^{2}-5=0} & {(\color{OliveGreen}{\sqrt{5}}\color{black}{)}^{2}-5=0} \\ {5-5=0} & {5-5=0} \\ {0=0 \color{Cerulean}{\checkmark}} & {0=0\color{Cerulean}{\checkmark}}\end{array}\)

Respuesta:
Las soluciones son\(-\sqrt{5}\) y\(\sqrt{5}\).

Ejemplo\(\PageIndex{3}\)

Resolver

Solución

Comience por aislar\(x^{2}\).

Aplicar la propiedad de raíz cuadrada y luego simplificar.

\(\begin{array}{l}{x=\pm \sqrt{\frac{45}{4}}} \\ {x=\pm \frac{\sqrt{9 \cdot 5}}{\sqrt{4}}} \\ {x=\pm \frac{3 \sqrt{5}}{2}}\end{array}\)

Respuesta:

Las soluciones son\(-\frac{3 \sqrt{5}}{2}\) y\(\frac{3 \sqrt{5}}{2}\).

A veces las ecuaciones cuadráticas no tienen una solución real.

Ejemplo\(\PageIndex{4}\)

Resolver:

\(x^{2} + 9 =0\)

Solución

Comience por aislar\(x^{2}\).

Después de aplicar la propiedad de raíz cuadrada, nos quedamos con la raíz cuadrada de un número negativo. Por lo tanto, no hay una solución real a esta ecuación.

Respuesta:

No hay solución real

Invierta este proceso para encontrar ecuaciones con soluciones dadas de la forma ±k.

Ejemplo\(\PageIndex{5}\)

Encuentra una ecuación con soluciones\(-2 \sqrt{3}\) y\(2 \sqrt{3}\).

Solución:

Comience por cuadrar ambos lados de la siguiente ecuación:

\(\begin{array}{l}{x=\pm 2 \sqrt{3}} \\ {x^{2}=( \pm 2 \sqrt{3})^{2}} \\ {x^{2}=4 \cdot 3} \\ {x^{2}=12}\end{array}\)

Por último, restar 12 de ambos lados y presentar la ecuación en forma estándar.

Respuesta:

\(x^{2}-12=0\)

Ejercicio\(\PageIndex{1}\)

Resolver:

\(9x^{2}-8=0\).

Contestar

\(x=-\frac{2 \sqrt{2}}{3}\)o\(x=\frac{2 \sqrt{2}}{3}\)

Considera resolver la siguiente ecuación:

\((x+2)^{2}=25\)

Para resolver esta ecuación factorizando, primero cuadrar x+2 y luego ponerla en forma estándar, igual a cero, restando 25 de ambos lados.

Factorizar y luego aplicar la propiedad de cero producto.

\(\begin{array}{c}{x^{2}+4 x-21=0} \\ {(x+7)(x-3)=0}\end{array}\)

\(\begin{array}{rr}{x+7=0} & {\text { or } \quad x-3=0} \\ {x=-7} & {x=3}\end{array}\)

Las dos soluciones son -7 y 3.

Cuando una ecuación está en esta forma, podemos obtener las soluciones en menos pasos extrayendo las raíces.

Ejemplo\(\PageIndex{6}\)

Resolver:

\((x=2)^{2}=25\).

Solución

Resuelve extrayendo las raíces.

\(\begin{array}{rlrr}{(x+2)^{2}} & {=25} & {\color{Cerulean}{ Apply\: the\:square \:root \:property.}} \\ {x+2} & {=\pm \sqrt{25}} & {\color{Cerulean}{ Simplify. }} \\ {x+2}& {=\pm5} \\ {x}&{=-2\pm5}\end{array}\)

En este punto, separe el “más o menos” en dos ecuaciones y simplifique cada una individualmente.

\(\begin{array}{ll}{x=-2-5} & {\text { or } x=-2+5} \\ {x=-7} & {\quad\:\: x=3}\end{array}\)

Respuesta:

Las soluciones son -7 y 3.

Además de menos pasos, este método nos permite resolver ecuaciones que no factorizan.

Ejemplo\(\PageIndex{7}\)

Resolver:

\((3 x+3)^{2}-27=0\)

Solución

Comience aislando el cuadrado.

\ (3 x+3) ^ {2} &=27\ end {alineado}\) </p">

A continuación, extraer las raíces y simplificar.

\(\begin{aligned}(3 x+3)^{2} &=27 \\ 3 x+3 &=\pm \sqrt{27} \\ 3 x+3 &=\pm \sqrt{9 \cdot 3} \\ 3 x+3 &=\pm 3 \sqrt{3} \end{aligned}\)

Resolver para x.

Respuesta:

Las soluciones son\(-1 - \sqrt{3}\) y\(-1 + \sqrt{3}\)

Ejemplo\(\PageIndex{8}\)

Resolver:

\(9(2 x-1)^{2}-8=0\)

Solución:

Comience aislando el factor cuadrado.

\ (2 x-1) ^ {2} &=\ frac {8} {9}\ end {alineado}\) </p">

Aplicar la propiedad de raíz cuadrada y resolver.

Respuesta:

Las soluciones son\(\frac{3 - 2 \sqrt{2}}{6}\) y\(\frac{3 + 2 \sqrt{2}}{6}\)

Ejercicio\(\PageIndex{2}\)

Resolver:

\(3(x-5)^{2}-2=0\)

Contestar

\(15\pm 6\sqrt{3}\)

Ejemplo\(\PageIndex{9}\)

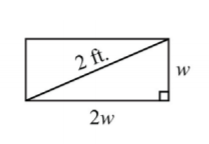
La longitud de un rectángulo es el doble de su ancho. Si la diagonal mide 2 pies, entonces encuentra las dimensiones del rectángulo.

Figura\(\PageIndex{1}\)

Solución

Deje que w represente el ancho.

Deje que 2w represente la longitud.

La diagonal de cualquier rectángulo forma dos triángulos rectos. Así se aplica el teorema de Pitágoras. La suma de los cuadrados de las patas de un triángulo rectángulo es igual al cuadrado de la hipotenusa:

\(\begin{array}{l}{(\operatorname{leg})^{2}+(\operatorname{leg})^{2}=\text { hypotenuse }^{2}} \\ {(\color{OliveGreen}{2 w}\color{black}{)}^{2}+(\color{OliveGreen}{w}\color{black}{)}^{2}=(\color{OliveGreen}{2}\color{black}{)}^{2}}\end{array}\)

Resolver.

\(\begin{aligned}(2 w)^{2}+(w)^{2} &=(2)^{2} \\ 4 w^{2}+w^{2} &=4 \\ 5 w^{2} &=4 \quad\quad\quad\color{Cerulean}{Isolate\:w^{2}.} \\\frac{5w^{2}}{\color{Cerulean}{5}}&\color{black}{=}\frac{4}{\color{Cerulean}{5}}\\ w^{2}&=\frac{4}{5}\quad\:\:\quad\color{Cerulean}{Extract\:the\:roots.} \\ w&=\pm\sqrt{\frac{4}{5}}\\w&=\pm\frac{2}{\sqrt{5}} \end{aligned}\)

Aquí obtenemos dos soluciones,\(w=−\frac{2}{\sqrt{5}}\) y\(w=\frac{2}{\sqrt{5}}\). Dado que el problema pedía una longitud de rectángulo, despreciamos la respuesta negativa. Además, racionalizaremos el denominador y presentaremos nuestras soluciones sin ningún radical en el denominador.

\(\begin{aligned} w &=\frac{2}{\sqrt{5}} \quad\quad\quad\quad\color{Cerulean}{Rationalize\:the\:denominator.} \\ &=\frac{2}{\sqrt{5}} \cdot \color{Cerulean}{\frac{\sqrt{5}}{\sqrt{5}}} \\ &=\frac{2 \sqrt{5}}{\sqrt{25}} \\ &=\frac{2 \sqrt{5}}{5} \end{aligned}\)

Volver sustituto para encontrar la longitud.

\(\begin{aligned} l &=2 w \\ &=2\color{black}{\left(\color{OliveGreen}{\frac{2 \sqrt{5}}{5}}\right)} \\ &=\frac{4 \sqrt{5}}{5} \end{aligned}\)

Respuesta:

El largo del rectángulo es\(\frac{4 \sqrt{5}}{5}\) pies y el ancho es\(\frac{2 \sqrt{5}}{5}\) pies.

Claves para llevar

• Resolver ecuaciones de la forma\(ax^{2}+c=0\) extrayendo las raíces.
• Extraer raíces implica aislar el cuadrado y luego aplicar la propiedad de raíz cuadrada. Después de aplicar la propiedad de raíz cuadrada, tiene dos ecuaciones lineales que cada una puede ser resuelta. Asegúrese de simplificar todas las expresiones radicales y racionalizar el denominador si es necesario.

Ejercicio\(\PageIndex{3}\) extracting square roots

Resuelve factorizando y luego resolviendo extrayendo raíces. Consulta las respuestas.

1. \(x^{2}-36=0\)
2. \(x^{2}-81=0\)
3. \(4y^{2}−9=0\)
4. \(9y^{2}−25=0\)
5. \((x−2)^{2}−1=0\)
6. \((x+1)^{2}−4=0\)
7. \(4(y−2)^{2}−9=0\)
8. \(9(y+1)^{2}−4=0\)
9. \(−3(t−1)^{2}+12=0\)
10. \(−2(t+1)^{2}+8=0\)
11. \((x−5)^{2}−25=0\)
12. \((x+2)^{2}−4=0\)

Contestar

1. \(-6, 6\)

3. \(-\frac{3}{2} , \frac{3}{2}\)

5. \(1, 3\)

7. \(\frac{1}{2}, \frac{7}{2}\)

9. \(-1, 3\)

11. \(0, 10\)

Ejercicio\(\PageIndex{4}\) extracting square roots

Resuelve extrayendo las raíces.

1. \(x^{2}=16\)
2. \(x^{2}=1\)
3. \(y^{2}=9\)
4. \(y^{2}=64\)
5. \(x^{2}=14\)
6. \(x^{2}=19\)
7. \(y^{2}=0.25\)
8. \(y^{2}=0.04\)
9. \(x^{2}=12\)
10. \(x^{2}=18\)
11. \(16x^{2}=9\)
12. \(4x^{2}=25\)
13. \(2t^{2} = 1\)
14. \(3t^{2} = 2\)
15. \(x^{2} −100 = 0\)
16. \(x^{2} −121 = 0\)
17. \(y^{2} + 4 = 0\)
18. \(y^{2} + 1 = 0\)
19. \(x^{2} −49 = 0\)
20. \(x^{2} −925 = 0\)
21. \(y^{2} −0.09 = 0\)
22. \(y^{2} −0.81 = 0\)
23. \(x^{2} − 7 = 0\)
24. \(x^{2} − 2 = 0\)
25. \(x^{2} − 8 = 0\)
26. \(t^{2} −18 = 0\)
27. \(x^{2} + 8 = 0\)
28. \(x^{2} +125 = 0\)
29. \(16x^{2} −27 = 0\)
30. \(9x^{2} − 8 = 0\)
31. \(2y^{2} − 3 = 0\)
32. \(5y^{2} − 2 = 0\)
33. \(3x^{2} − 1 = 0\)
34. \(6x^{2} − 3 = 0\)
35. \((x + 7 )^{2} − 4 = 0\)
36. \((x + 9 )^{2} −36 = 0\)
37. \(( 2y − 3 )^{2} −81 = 0 \)
38. \(( 2y + 1 )^{2} −25 = 0\)
39. \((x − 5 )^{2} −20 = 0\)
40. \((x + 1 )^{2} −28 = 0\)
41. \(( 3t + 2 )^{2} − 6 = 0\)
42. \((3t−5)^{2}−10=0\)
43. \(4(y+2)^{2}−3=0\)
44. \(9(y−7)^{2}−5=0\)
45. \(4(3x+1)^{2}−27=0\)
46. \(9(2x−3)^{2}−8=0\)
47. \(2(3x−1)^{2}+3=0\)
48. \(5(2x−1)^{2}−3=0\)
49. \(3(y−23)^{2}−32=0\)
50. \(2(3y−13)^{2}−52=0\)

Contestar

1. ±4

3. ±3

5. ±\(\frac{1}{2}\)

7. ±0.5

9. ±\(2\sqrt{3}\)

11. ±\(\frac{3}{4}\)

13. ±\(\sqrt{\frac{1}{2}}\)

15. ±10

17. No hay solución real

19. ±\(\frac{2}{3}\)

21. ±0.3

23. ±\(\sqrt{7}\)

25. ±\(2\sqrt{2}\)

27. No hay solución real

29. ±\(\frac{3 \sqrt{3}}{4}\)

31. ±\(6\sqrt{2}\)

33. ±\(3\sqrt{3}\)

35. \(−9, −5\)

37. \(−3, 6\)

39. \(5\)±\(2\sqrt{5}\)

41. ±\(\frac{\sqrt{6}-2}{3}\)

43. ±\(\frac{\sqrt{3}}{2}-2\)

45. ±\(\frac{3 \sqrt{3}-2}{6}\)

47. No hay solución real

49. ±\(\frac{4 \sqrt{6}}{3}+23\)

Ejercicio\(\PageIndex{5}\) extracting square roots

Encuentra una ecuación cuadrática en forma estándar con las siguientes soluciones.

1. ±7
2. ±13
3. ±\(\sqrt{7}\)
4. ±\(\sqrt{3}\)
5. ±\(3\sqrt{5}\)
6. ±\(5\sqrt{2}\)
7. \(1\)±\(\sqrt{2}\)
8. \(2\)±\(\sqrt{3}\)

Contestar

1. \(x^{2}−49=0\)

3. \(x^{2}−7=0\)

5. \(x^{2}−45=0\)

7. \(x^{2}−2x−1=0\)

Ejercicio\(\PageIndex{6}\) extracting square roots

Resuelve y redondea las soluciones a la centésima más cercana.

1. \(9x(x+2)=18x+1\)
2. \(x^{2}=10(x^{2}−2)−5\)
3. \((x+3)(x−7)=11−4x\)
4. \((x−4)(x−3)=66−7x\)
5. \((x−2)^{2}=67−4x\)
6. \((x+3)^{2}=6x+59\)
7. \((2x+1)(x+3)−(x+7)=(x+3)^{2}\)
8. \((3x−1)(x+4)=2x(x+6)−(x−3)\)

Contestar

1. ±0.33

3. ±5.66

5. ±7.94

7. ±3.61

Ejercicio\(\PageIndex{7}\) extracting square roots

Configura una ecuación algebraica y úsala para resolver lo siguiente.

1. Si se resta 9 de 4 veces el cuadrado de un número, entonces el resultado es 3. Encuentra el número.
2. Si se resta 20 del cuadrado de un número, entonces el resultado es 4. Encuentra el número.
3. Si se agrega 1 a 3 veces el cuadrado de un número, entonces el resultado es 2. Encuentra el número.
4. Si se agrega 3 a 2 veces el cuadrado de un número, entonces el resultado es 12. Encuentra el número.
5. Si un cuadrado tiene un área de 8 centímetros cuadrados, entonces encuentra la longitud de cada lado.
6. Si un círculo tiene un área de 32 centímetros\(\pi\) cuadrados, entonces encuentra la longitud del radio.
7. El volumen de un cono circular derecho es de 36 centímetros\(\pi\) cúbicos cuando la altura es de 6 centímetros. Encuentra el radio del cono. (El volumen de un cono circular derecho viene dado por\(V=13\pi r^{2}h\).)
8. La superficie de una esfera es de 75 centímetros\(\pi\) cuadrados. Encuentra el radio de la esfera. (La superficie de una esfera viene dada por SA=\(4\pi r^{2}\).)
9. La longitud de un rectángulo es 6 veces su ancho. Si el área es de 96 pulgadas cuadradas, entonces encuentra las dimensiones del rectángulo.
10. La base de un triángulo es el doble de su altura. Si el área es de 16 centímetros cuadrados, entonces encuentra la longitud de su base.
11. Una plaza tiene una superficie de 36 unidades cuadradas. ¿En qué cantidad igual habrá que aumentar los lados para crear un cuadrado con el doble de área dada?
12. Un círculo tiene una superficie de 25 unidades\(\pi\) cuadradas. ¿En qué cantidad habrá que aumentar el radio para crear un círculo con el doble del área dada?
13. Si los lados de un cuadrado miden 1 unidad, entonces encuentra la longitud de la diagonal.
14. Si los lados de un cuadrado miden 2 unidades, entonces encuentra la longitud de la diagonal.
15. La diagonal de un cuadrado mide 5 pulgadas. Encuentra la longitud de cada lado.
16. La diagonal de un cuadrado mide 3 pulgadas. Encuentra la longitud de cada lado.
17. La longitud de un rectángulo es el doble de su ancho. Si la diagonal mide 10 pies, entonces encuentra las dimensiones del rectángulo.
18. La longitud de un rectángulo es el doble de su ancho. Si la diagonal mide 8 pies, entonces encuentra las dimensiones del rectángulo.
19. La longitud de un rectángulo es 3 veces su ancho. Si la diagonal mide 5 metros, entonces encuentra las dimensiones del rectángulo.
20. La longitud de un rectángulo es 3 veces su ancho. Si la diagonal mide 2 pies, entonces encuentra las dimensiones del rectángulo.
21. La altura en pies de un objeto caído desde una escalera de 9 pies viene dada por h (t)\(=−16t^{2}+9\), donde t representa el tiempo en segundos después de que el objeto ha sido caído. ¿Cuánto tiempo tarda el objeto en golpear el suelo? (Pista: La altura es 0 cuando el objeto golpea el suelo.)
22. La altura en pies de un objeto caído desde una plataforma de 20 pies viene dada por h (t)\(=−16t^{2}+20\), donde t representa el tiempo en segundos después de que el objeto ha sido caído. ¿Cuánto tiempo tarda el objeto en golpear el suelo?
23. La altura en pies de un objeto caído desde la parte superior de un edificio de 144 pies viene dada por h (t)\(=−16t^{2}+144\), donde t se mide en segundos.
    1. ¿Cuánto tiempo tardará en llegar a la mitad de la distancia al suelo, 72 pies?
    2. ¿Cuánto tiempo tardará en recorrer el resto de la distancia hasta el suelo? Redondear a la centésima de segundo más cercana.
24. La altura en pies de un objeto caído desde un avión a 1,600 pies viene dada por h (t)\(=−16t^{2}+1,600\), donde t está en segundos.
    1. ¿Cuánto tiempo tardará en llegar a la mitad de la distancia al suelo?
    2. ¿Cuánto tiempo tardará en recorrer el resto de la distancia hasta el suelo? Redondear a la centésima de segundo más cercana.
25. Crea una ecuación propia que pueda resolverse extrayendo la raíz. Compártelo, junto con la solución, en el panel de discusión.
26. Explicar por qué la técnica de extracción de raíces expande enormemente nuestra capacidad para resolver ecuaciones cuadráticas.
27. Explica con tus propias palabras cómo resolver extrayendo las raíces. 106. Derivar una fórmula para la diagonal de un cuadrado en términos de sus lados.

Contestar

1. \(−\sqrt{3}\)o\(\sqrt{3}\)

3. \(−3\sqrt{3}\)o\(3\sqrt{3}\)

5. \(2\sqrt{2}\)centímetros

7. \(3\sqrt{2}\)centímetros

9. Largo: 24 pulgadas; ancho: 4 pulgadas

11. \(−6+6\sqrt{2}\approx 2.49\)unidades

13. \(\sqrt{2}\)unidades

15. \(52\sqrt{2}\)pulgadas

17. Largo:\(4\sqrt{5}\) pies; ancho:\(2\sqrt{5}\) pies

19. Largo:\(310−−\sqrt{2}\) metros; ancho:\(10−−\sqrt{2}\) metros

21. \(\frac{3}{4}\)segundo

23. a. 2.12 segundos b. 0.88 segundos

25. Las respuestas pueden variar