7.1: Composición y funciones inversas

Objetivos de aprendizaje

• Realizar composición de funciones.
• Determinar si las funciones dadas son inversas o no.
• Utilice la prueba de línea horizontal.
• Encuentra la inversa de una función uno a uno algebraicamente.

Composición de las funciones

En matemáticas, suele darse el caso de que el resultado de una función se evalúa aplicando una segunda función. Por ejemplo, considere las funciones definidas por\(f(x)=x^{2}\) y\(g(x)=2x+5\). En primer lugar,\(g\) se evalúa donde\(x=−1\) y luego el resultado es cuadrado usando la segunda función,\(f\).

Figura\(\PageIndex{1}\)

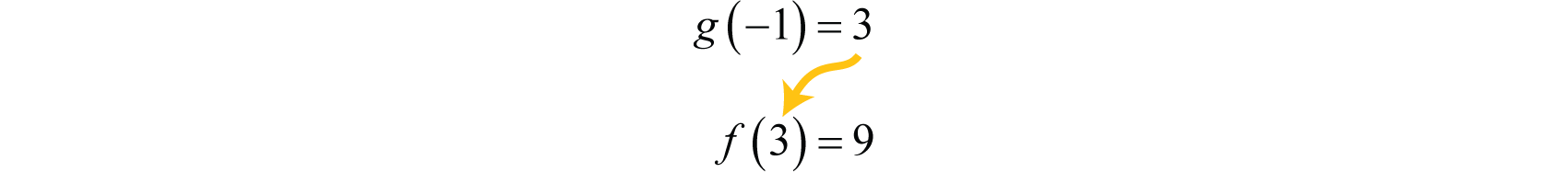
Este cálculo secuencial da como resultado\(9\). Podemos agilizar este proceso creando una nueva función definida por\(f(g(x))\), que se obtiene explícitamente sustituyendo\(g(x)\) en\(f(x)\).

\(\begin{aligned} f(\color{Cerulean}{g(x)}\color{black}{)} &=f(\color{Cerulean}{2 x+5}\color{black}{)} \\ &=(2 x+5)^{2} \\ &=4 x^{2}+20 x+25 \end{aligned}\)

Por lo tanto,\(f(g(x))=4x^{2}+20x+25\) y podemos verificar que cuando\(x=−1\) el resultado sea\(9\).

\(\begin{aligned} f(g(\color{Cerulean}{-1}\color{black}{)}) &=4(\color{Cerulean}{-1}\color{black}{)}^{2}+20(\color{Cerulean}{-1}\color{black}{)}+25 \\ &=4-20+25 \\ &=9 \end{aligned}\)

El cálculo anterior describe la composición de las funciones ¹, la cual se indica utilizando el operador de composición ²\((○)\). Si se le dan funciones\(f\) y\(g\),

\((f \circ g)(x)=f(g(x)) \quad \color{Cerulean}{Composition\:of\:Functions}\)

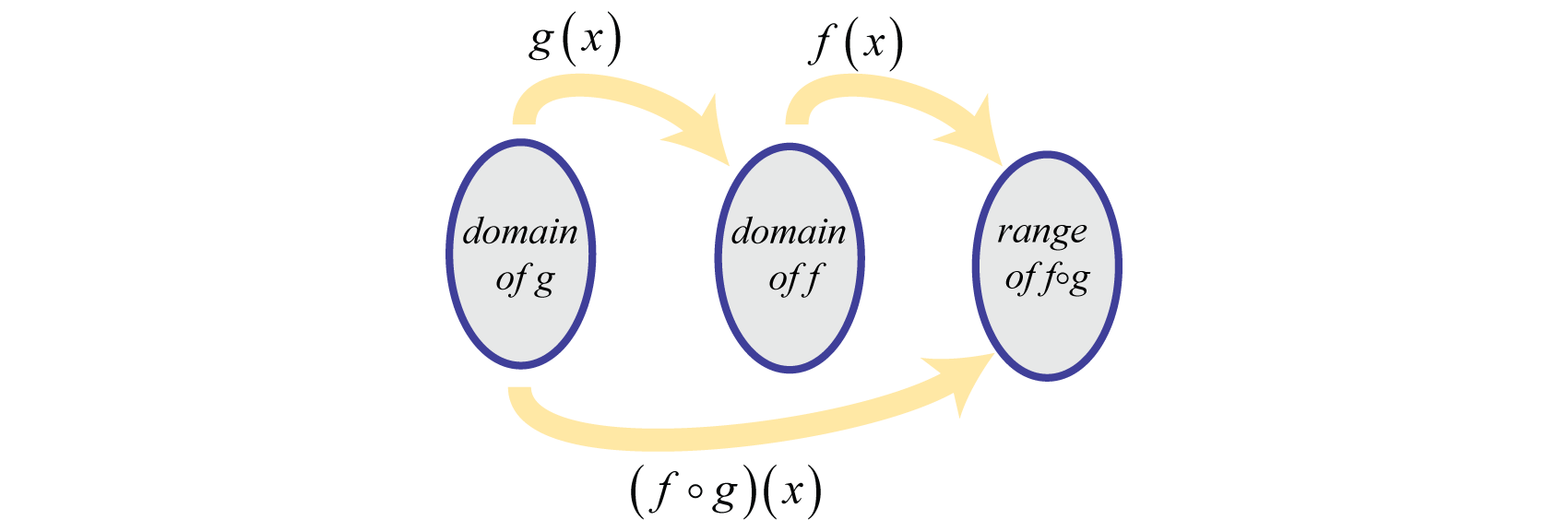
\(f○g\)Se lee la notación, “\(f\)compuesta con”\(g\). Esta operación sólo se define para valores, \(x\), en el dominio de\(g\) tal que\(g(x)\) está en el dominio de\(f\).

Figura\(\PageIndex{2}\)

Ejemplo\(\PageIndex{1}\):

Dado\(f(x)=x^{2}−x+3\) y\(g(x)=2x−1\) calcular:

1. \((f○g)(x)\).
2. \((g○f)(x)\).

Solución

1. Sustituir\(g\) en\(f\).

   \(\begin{aligned}(f \circ g)(x) &=f(g(x)) \\ &=f(\color{Cerulean}{2 x-1}\color{black}{)} \\ &=(\color{Cerulean}{2 x-1}\color{black}{)}^{2}-(\color{Cerulean}{2 x-1}\color{black}{)}+3 \\ &=4 x^{2}-4 x+1-2 x+1+3 \\ &=4 x^{2}-6 x+5 \end{aligned}\)

2. Sustituir\(f\) en\(g\).

   \(\begin{aligned}(g \circ f)(x) &=g(f(x)) \\ &=g\color{black}{\left(\color{Cerulean}{x^{2}-x+3}\right)} \\ &=2\color{black}{\left(\color{Cerulean}{x^{2}-x+3}\right)}-1 \\ &=2 x^{2}-2 x+6-1 \\ &=2 x^{2}-2 x+5 \end{aligned}\)

Respuesta:

1. \((f○g)(x)=4x^{2}−6x+5\)
2. \((g○f)(x)=2x^{2}−2x+5\)

El ejemplo anterior muestra que la composición de funciones no es necesariamente conmutativa.

Ejemplo\(\PageIndex{2}\)

Dado\(f(x)=x^{3}+1\) y\(g(x)=\sqrt[3]{3 x-1}\) encontrar\((f○g)(4)\).

Solución

Comience por encontrar\((f○g)(x)\).

\(\begin{aligned}(f \circ g)(x) &=f(g(x)) \\ &=f(\color{Cerulean}{\sqrt[3]{3 x-1}}\color{black}{)} \\ &=(\color{Cerulean}{\sqrt[3]{3 x-1}}\color{black}{)}^{3}+1 \\ &=3 x-1+1 \\ &=3 x \end{aligned}\)

A continuación, sustituya\(4\) en\(x\).

\(\begin{aligned}(f \circ g)(x) &=3 x \\(f \circ g)(\color{Cerulean}{4}\color{black}{)} &=3(\color{Cerulean}{4}\color{black}{)} \\ &=12 \end{aligned}\)

Respuesta:

\((f○g)(4)=12\)

Las funciones se pueden componer consigo mismas.

Ejemplo\(\PageIndex{3}\)

Dado\(f(x)=x^{2}−2\) hallazgo\((f○f)(x)\).

Solución

\(\begin{aligned}(f \circ f)(x) &=f(\color{Cerulean}{f(x)}\color{black}{)} \\ &=f\color{black}{\left(\color{Cerulean}{x^{2}-2}\right)} \\ &=\color{black}{\left(\color{Cerulean}{x^{2}-2}\right)}^{2}-2 \\ &=x^{4}-4 x^{2}+4-2 \\ &=x^{4}-4 x^{2}+2 \end{aligned}\)

Respuesta:

\((f \circ f)(x)=x^{4}-4 x^{2}+2\)

Ejercicio\(\PageIndex{1}\)

Dado\(f(x)=2x+3\) y\(g(x)=\sqrt{x-1}\) encontrar\((f○g)(5)\).

Contestar

\(7\)

www.youtube.com/v/cwegsja5tlc

Funciones inversas

Considera la función que convierte grados Fahrenheit a grados Celsius:\(C(x)=\frac{5}{9}(x-32)\). Podemos usar esta función para convertir\(77\) °F a grados Celsius de la siguiente manera.

\(\begin{aligned} C(\color{OliveGreen}{77}\color{black}{)} &=\frac{5}{9}(\color{OliveGreen}{77}\color{black}{-}32) \\ &=\frac{5}{9}(45) \\ &=25 \end{aligned}\)

Por lo tanto,\(77\) °F es equivalente a\(25\) °C. Si deseamos convertir\(25\) °C de nuevo a grados Fahrenheit usaríamos la fórmula:\(F(x)=\frac{9}{5}x+32\).

\(\begin{aligned} F(\color{OliveGreen}{25}\color{black}{)} &=\frac{9}{5}(\color{OliveGreen}{25}\color{black}{)}+32 \\ &=45+32 \\ &=77 \end{aligned}\)

Observe que las dos funciones\(C\) y\(F\) cada una revierten el efecto de la otra.

Figura\(\PageIndex{3}\)

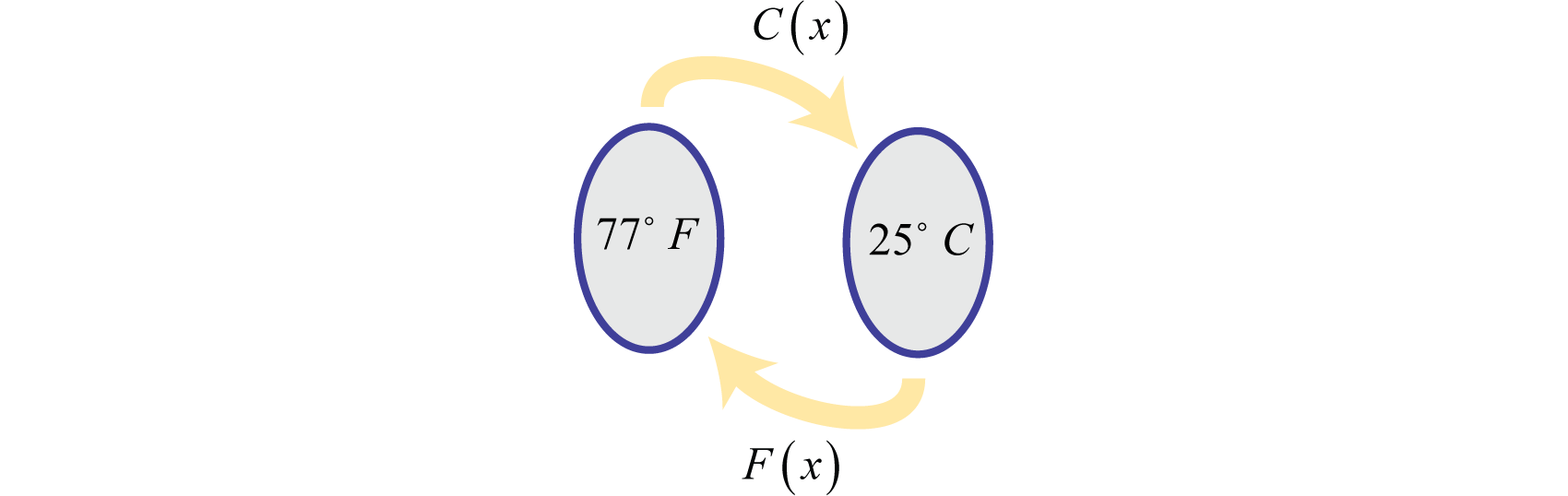
Esto describe una relación inversa. En general,\(f\) y\(g\) son funciones inversas si,

\(\begin{aligned}(f \circ g)(x)&=f(g(x))=x\quad\color{Cerulean}{for\:all\:x\:in\:the\:domain\:of\:g\:and} \\ (g \mathrm{O} f)(x)&=g(f(x))=x\quad\color{Cerulean}{for\:all\:x\:in\:the\:domain\:of\:f.}\end{aligned}\)

En este ejemplo,

\(\begin{aligned} C(F(\color{Cerulean}{25}\color{black}{)}) &=C(77)=\color{Cerulean}{25} \\ F(C(\color{Cerulean}{77}\color{black}{)}) &=F(25)=\color{Cerulean}{77} \end{aligned}\)

Ejemplo\(\PageIndex{4}\)

Verificar algebraicamente que las funciones definidas por\(f(x)=\frac{1}{2}x−5\) y\(g(x)=2x+10\) son inversas.

Solución

Redactar las funciones en ambos sentidos y verificar que el resultado es\(x\).

Mesa\(\PageIndex{1}\)

\(\begin{aligned}(f \circ g)(x) &=f(g(x)) \\ &=f(\color{Cerulean}{2 x+10}\color{black}{)} \\ &=\frac{1}{2}(\color{Cerulean}{2 x+10}\color{black}{)}-5 \\ &=x+5-5 \\ &=x\:\:\color{Cerulean}{✓} \end{aligned}\)

\(\begin{aligned}(g \text { Of })(x) &=g(f(x)) \\ &=g\color{black}{\left(\color{Cerulean}{\frac{1}{2} x-5}\right)} \\ &=2\color{black}{\left(\color{Cerulean}{\frac{1}{2} x-5}\right)}+10 \\ &=x-10+10 \\ &=x\:\:\color{Cerulean}{✓} \end{aligned}\)

Respuesta:

Ambos\((f \circ g)(x)=(g \circ f)(x)=x\); por lo tanto, son inversos.

A continuación exploramos la geometría asociada a las funciones inversas. Las gráficas de ambas funciones en el ejemplo anterior se proporcionan en el mismo conjunto de ejes a continuación.

Figura\(\PageIndex{4}\)

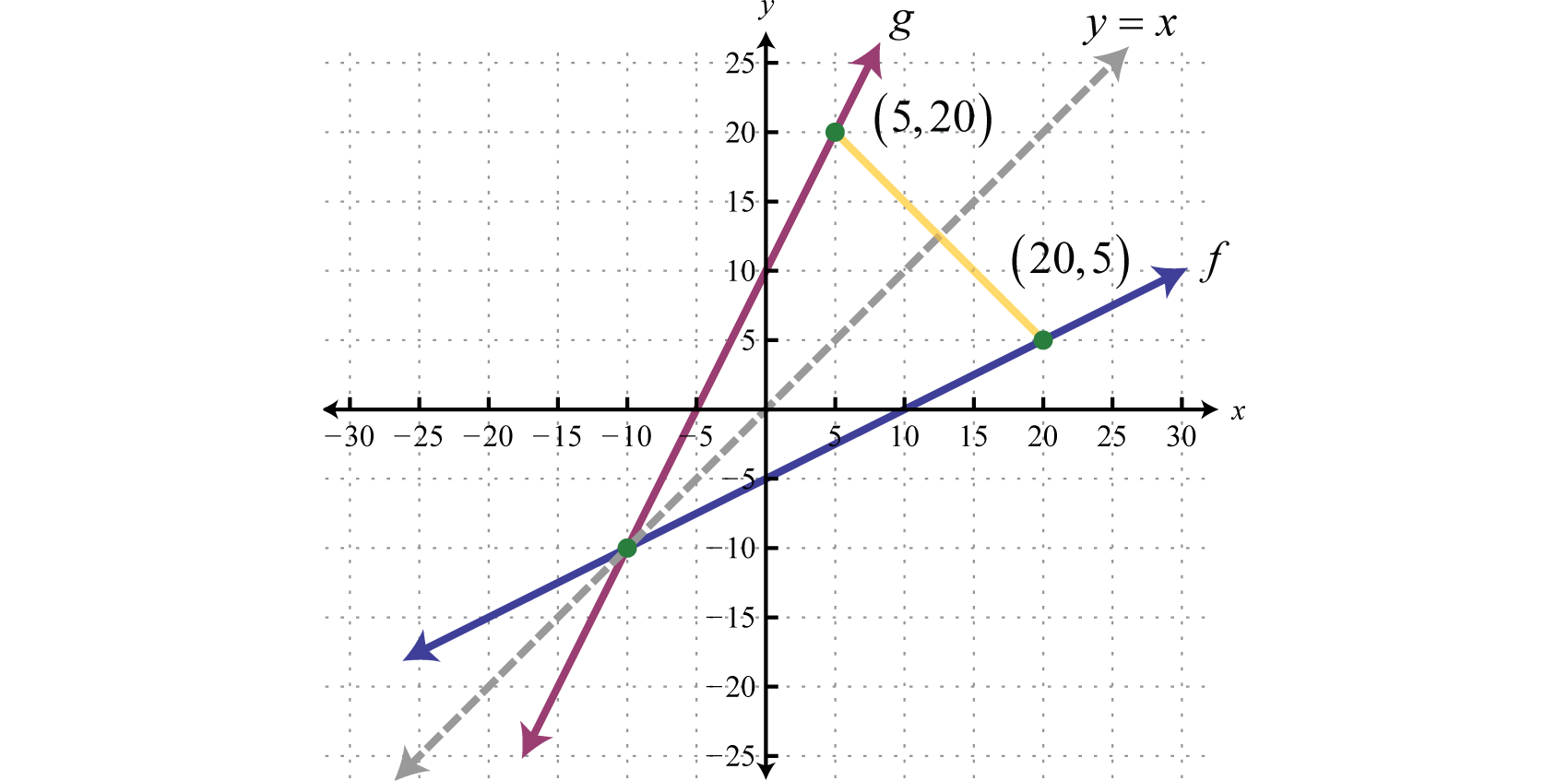
Tenga en cuenta que hay simetría sobre la línea\(y=x\); las gráficas de\(f\) y\(g\) son imágenes especular sobre esta línea. También fíjese que el punto\((20, 5)\) está en la gráfica de\(f\) y que\((5, 20)\) está en la gráfica de\(g\). Ambas observaciones son ciertas en general y tenemos las siguientes propiedades de funciones inversas:

1. Las gráficas de funciones inversas son simétricas sobre la línea\(y=x\).
2. Si\((a,b)\) está en la gráfica de una función, entonces\((b,a)\) está en la gráfica de su inversa.

Además, si\(g\) es la inversa de\(f\) usamos la notación\(g=f^{-1}\). Aquí\(f^{-1}\) se lee, “\(f\)inverso”, y no debe confundirse con exponentes negativos. En otras palabras,\(f^{-1}(x) \neq \frac{1}{f(x)}\) y tenemos,

\(\begin{array}{l}{\left(f \circ f^{-1}\right)(x)=f\left(f^{-1}(x)\right)=x \text { and }} \\ {\left(f^{-1} \circ f\right)(x)=f^{-1}(f(x))=x}\end{array}\)

Ejemplo\(\PageIndex{5}\):

Verificar algebraicamente que las funciones definidas por\(f(x)=\frac{1}{x}−2\) y\(f^{-1}(x)=\frac{1}{x+2}\) son inversas.

Solución

Redactar las funciones de ambas maneras para verificar que el resultado es\(x\).

Mesa\(\PageIndex{2}\)

\(\begin{aligned}\left(f \circ f^{-1}\right)(x) &=f\left(f^{-1}(x)\right) \\ &=f\color{black}{\left(\color{Cerulean}{\frac{1}{x+2}}\right)} \\ &=\frac{1}{\color{black}{\left(\color{Cerulean}{\frac{1}{x+2}}\right)}}-2 \\ &=\frac{x+2}{1}-2 \\ &=x+2-2 \\ &=x\:\:\color{Cerulean}{✓} \end{aligned}\)

\(\begin{aligned}\left(f^{-1} \circ f\right)(x) &=f^{-1}(f(x)) \\ &=f^{-1}\color{black}{\left(\color{Cerulean}{\frac{1}{x}-2}\right)} \\ &=\frac{1}{\color{black}{\left(\color{Cerulean}{\frac{1}{x}-2}\right)}+2} \\ &=\frac{1}{\frac{1}{x}} \\ &=x\:\:\color{Cerulean}{✓} \end{aligned}\)

Respuesta:

Ya\(\left(f \circ f^{-1}\right)(x)=\left(f^{-1} \circ f\right)(x)=x\) que son inversos.

Recordemos que una función es una relación donde cada elemento en el dominio corresponde exactamente a un elemento en el rango. Utilizamos la prueba de línea vertical para determinar si una gráfica representa una función o no. Las funciones se pueden clasificar adicionalmente usando una relación inversa. Las funciones uno a uno ³ son funciones donde cada valor en el rango corresponde exactamente a un elemento en el dominio. La prueba de línea horizontal ⁴ se utiliza para determinar si un gráfico representa o no una función uno a uno. Si una línea horizontal cruza una gráfica más de una vez, entonces no representa una función uno a uno.

Figura\(\PageIndex{5}\)

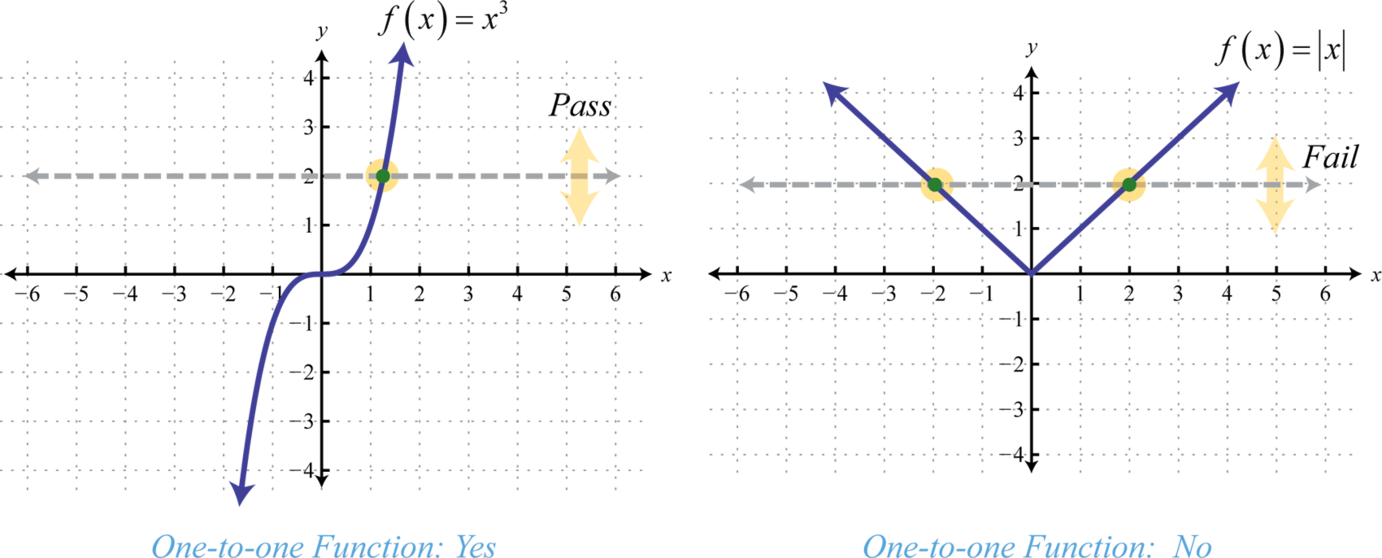
La línea horizontal representa un valor en el rango y el número de intersecciones con la gráfica representa el número de valores a los que corresponde en el dominio. La función definida por\(f(x)=x^{3}\) es uno a uno y la función definida por no\(f(x)=|x|\) es. Determinar si una función es uno a uno o no es importante porque una función tiene un inverso si y solo si es uno a uno. En otras palabras, una función tiene una inversa si pasa la prueba de línea horizontal.

Nota

En este texto, cuando decimos “una función tiene una inversa”, queremos decir que hay otra función,\(f^{−1}\), tal que\((f○f^{−1})(x)=(f^{−1}○f)(x)=x\).

Ejemplo\(\PageIndex{6}\):

Determine si la función dada es uno a uno o no.

Figura\(\PageIndex{6}\)

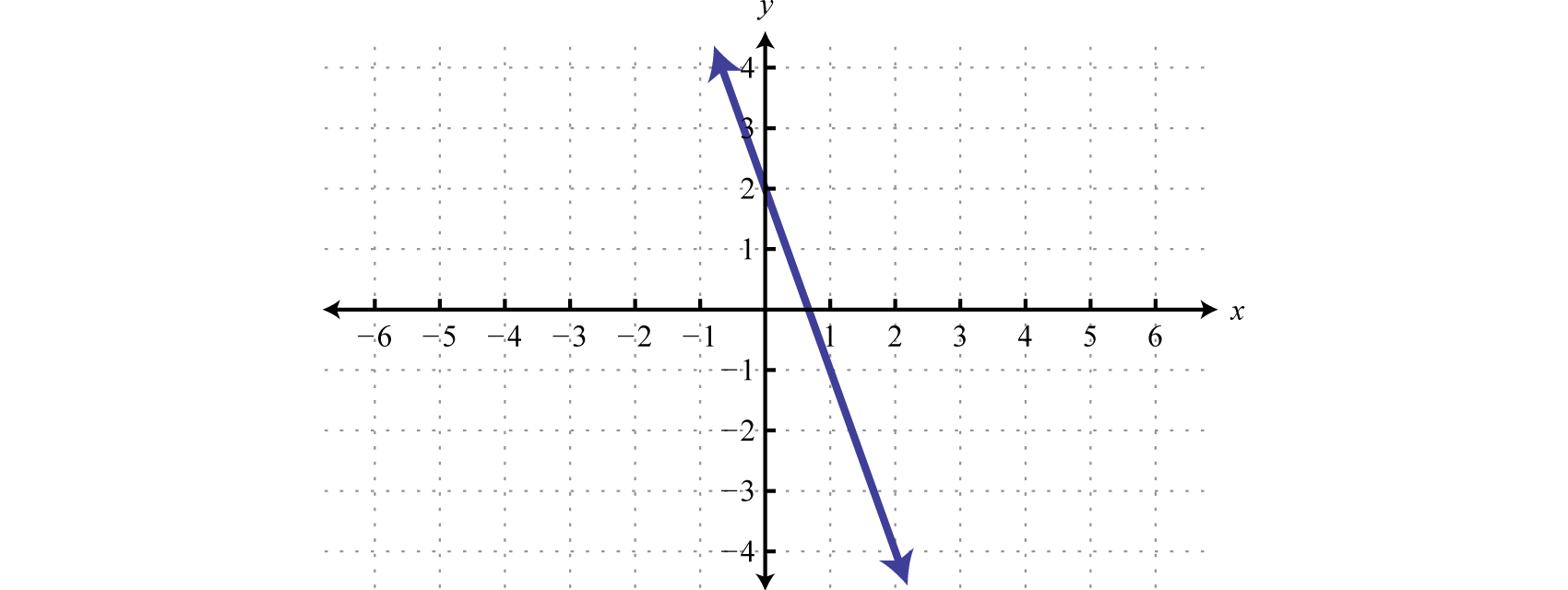
Solución

Figura\(\PageIndex{7}\)

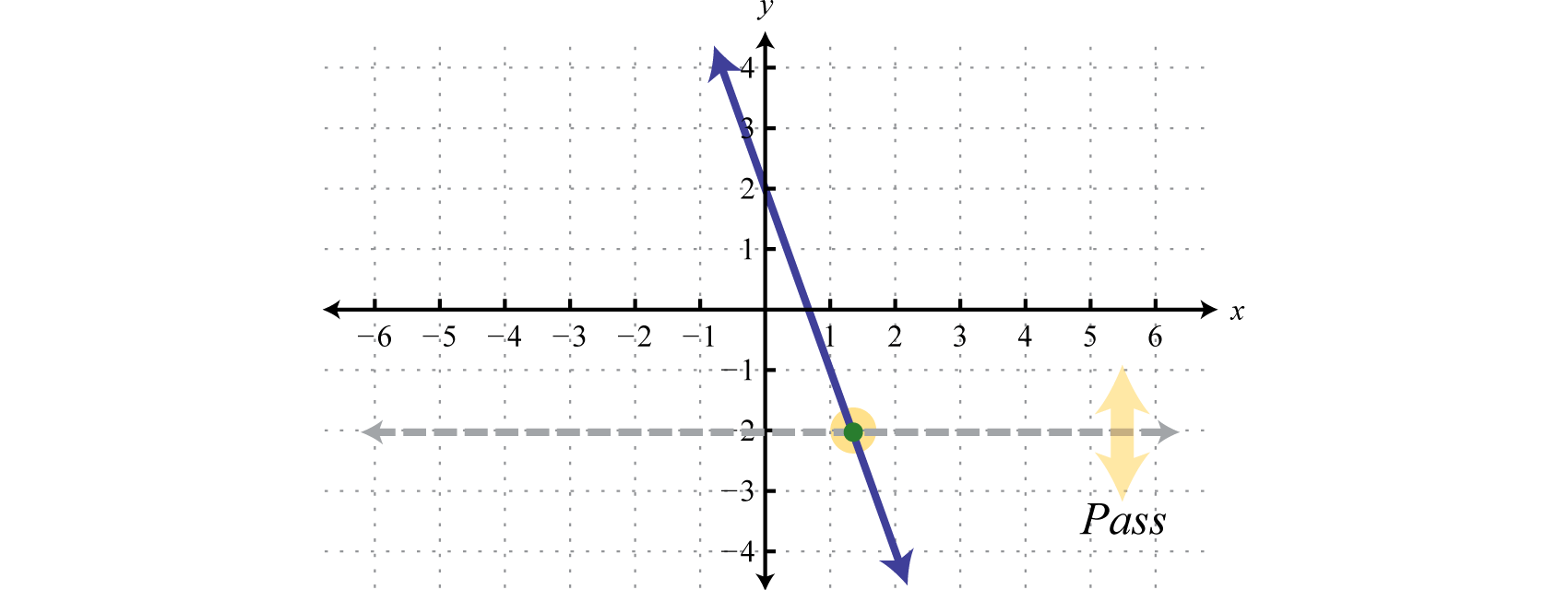
Respuesta:

La función dada pasa la prueba de línea horizontal y por lo tanto es uno a uno.

De hecho, cualquier función lineal de la forma\(f(x)=mx+b\) donde\(m≠0\), es uno a uno y por lo tanto tiene una inversa. Los pasos para encontrar la inversa de una función uno a uno se describen en el siguiente ejemplo.

Ejemplo\(\PageIndex{7}\)

Encuentra la inversa de la función definida por\(f(x)=\frac{3}{2}x−5\).

Solución

Antes de comenzar este proceso, debe verificar que la función es uno a uno. En este caso, tenemos una función lineal donde\(m≠0\) y por lo tanto es uno-a-uno.

Paso 1: Reemplazar la notación\(f(x)\) de la función por\(y\).

\(\begin{aligned}f(x)&=\frac{3}{2} x-5 \\ y&=\frac{3}{2} x-5\end{aligned}\)

Paso 2: Intercambio\(x\) y\(y\). Utilizamos el hecho de que si\((x,y)\) es un punto en la gráfica de una función, entonces\((y,x)\) es un punto en la gráfica de su inversa.

\(x=\frac{3}{2} y-5\)

Paso 3: Resolver para\(y\).

\(\begin{aligned} x &=\frac{3}{2} y-5 \\ x+5 &=\frac{3}{2} y \\ \\\color{Cerulean}{\frac{2}{3}}\color{black}{ \cdot}(x+5) &=\color{Cerulean}{\frac{2}{3}}\color{black}{ \cdot} \frac{3}{2} y \\ \frac{2}{3} x+\frac{10}{3} &=y \end{aligned}\)

Paso 4: La función resultante es la inversa de\(f\). Reemplazar\(y\) con\(f^{−1}(x)\).

\(f^{-1}(x)=\frac{2}{3} x+\frac{10}{3}\)

Paso 5: Comprobar.

Mesa\(\PageIndex{3}\)

\(\begin{array}{l}{\left(f \circ f^{-1}\right)(x)} \\ {=f\left(f^{-1}(x)\right)} \\ {=f\color{black}{\left(\color{Cerulean}{\frac{2}{3} x+\frac{10}{3}}\right)}} \\ {=\frac{3}{2}\color{black}{\left(\color{Cerulean}{\frac{2}{3} x+\frac{10}{3}}\right)}-5} \\ {=x+5-5} \\ {=x}\:\:\color{Cerulean}{✓}\end{array}\)

\(\begin{array}{l}{\left(f^{-1} \circ f\right)(x)} \\ {=f^{-1}(f(x))} \\ {=f^{-1}\color{black}{\left(\color{Cerulean}{\frac{3}{2} x-5}\right)}} \\ {=\frac{2}{3}\color{black}{\left(\color{Cerulean}{\frac{3}{2} x-5}\right)}+\frac{10}{3}} \\ {=x-\frac{10}{3}+\frac{10}{3}} \\ {=x} \:\:\color{Cerulean}{✓}\end{array}\)

Respuesta:

\(f^{-1}(x)=\frac{2}{3} x+\frac{10}{3}\)

Si una función no es uno a uno, suele darse el caso de que podemos restringir el dominio de tal manera que el gráfico resultante sea uno a uno. Por ejemplo, considere la función de cuadratura desplazada hacia arriba una unidad,\(g(x)=x^{2}+1\). Tenga en cuenta que no pasa la prueba de línea horizontal y por lo tanto no es uno a uno. Sin embargo, si restringimos el dominio a valores no negativos\(x≥0\), entonces la gráfica sí pasa la prueba de línea horizontal.

Figura\(\PageIndex{8}\)

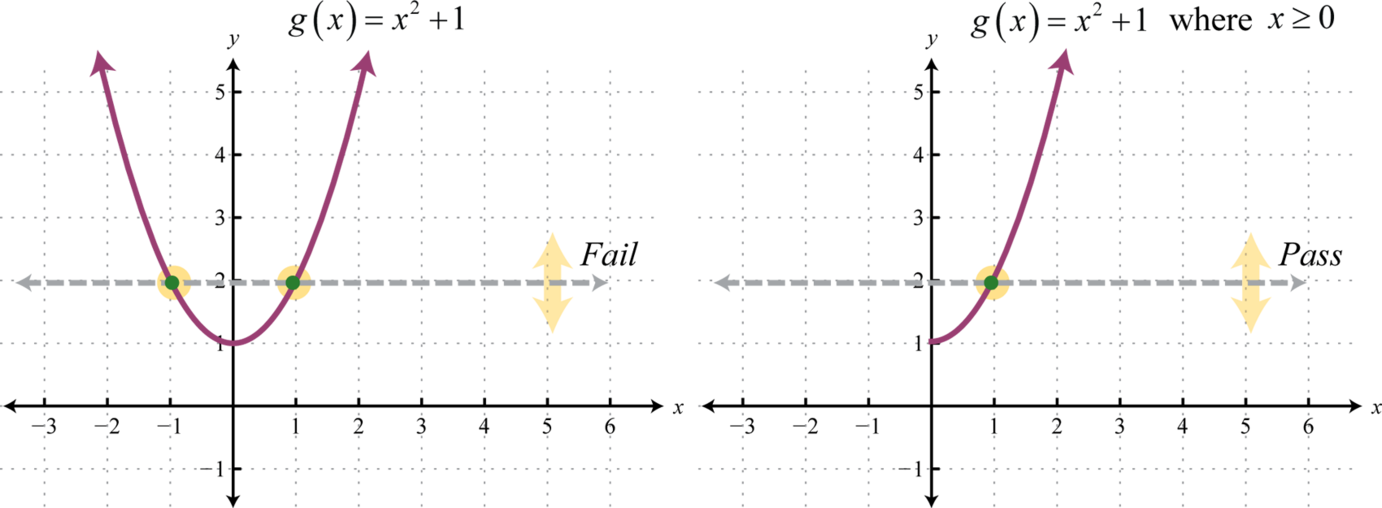
En el dominio restringido,\(g\) es uno a uno y podemos encontrar su inversa.

Ejemplo\(\PageIndex{8}\):

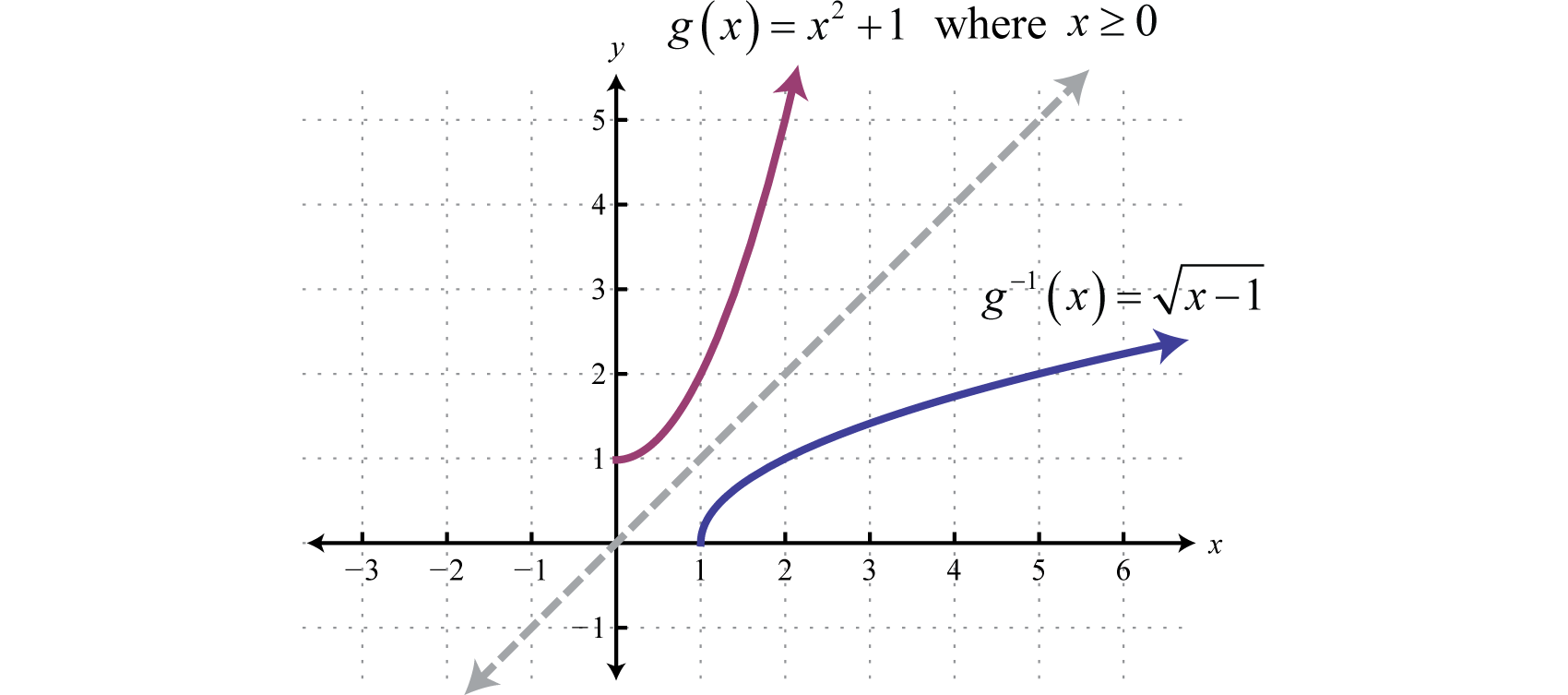
Encuentra la inversa de la función definida por\(g(x)=x^{2}+1\) donde\(x≥0\).

Solución

Comience reemplazando la notación de función\(g(x)\) con\(y\).

\(\begin{aligned} g(x) &=x^{2}+1 \\ y &=x^{2}+1 \text { where } x \geq 0 \end{aligned}\)

Intercambio\(x\) y\(y\).

\(x=y^{2}+1\)donde\(y \geq 0\)

Resolver para\(y\).

\(\begin{aligned} x &=y^{2}+1 \\ x-1 &=y^{2} \\ \pm \sqrt{x-1} &=y \end{aligned}\)

Ya\(y≥0\) que sólo consideramos el resultado positivo.

\(\begin{aligned} y &=\sqrt{x-1} \\ g^{-1}(x) &=\sqrt{x-1} \end{aligned}\)

Respuesta:

\(g^{-1}(x)=\sqrt{x-1}\). El cheque se deja al lector.

Las gráficas del ejemplo anterior se muestran en el mismo conjunto de ejes a continuación. Toma nota de la simetría sobre la línea\(y=x\).

Figura\(\PageIndex{9}\)

Ejemplo\(\PageIndex{9}\):

Encuentra la inversa de la función definida por\(f(x)=\frac{2 x+1}{x-3}\).

Solución

Utilice una utilidad gráfica para verificar que esta función es uno a uno. Comience reemplazando la notación de función\(f(x)\) con\(y\).

\(\begin{aligned} f(x) &=\frac{2 x+1}{x-3} \\ y &=\frac{2 x+1}{x-3} \end{aligned}\)

Intercambio\(x\) y\(y\).

\(x=\frac{2 y+1}{y-3}\)

Resolver para\(y\).

\(\begin{aligned} x &=\frac{2 y+1}{y-3} \\ x(y-3) &=2 y+1 \\ x y-3 x &=2 y+1 \end{aligned}\)

Obtener todos los términos con la variable\(y\) en un lado de la ecuación y todo lo demás en el otro. Esto nos permitirá tratar\(y\) como un GCF.

\(\begin{aligned} x y-3 x &=2 y+1 \\ x y-2 y &=3 x+1 \\ y(x-2) &=3 x+1 \\ y &=\frac{3 x+1}{x-2} \end{aligned}\)

Respuesta:

\(f^{-1}(x)=\frac{3 x+1}{x-2}\). El cheque se deja al lector.

Ejercicio\(\PageIndex{2}\)

Encuentra la inversa de\(f(x)=\sqrt[3]{x+1}-3\).

Contestar

\(f^{-1}(x)=(x+3)^{3}-1\)

www.youtube.com/v/mwsb9wuyfca

Claves para llevar

• El operador de composición\((○)\) indica que debemos sustituir una función por otra. En otras palabras,\((f○g)(x)=f(g(x))\) indica que sustituimos\(g(x)\) en\(f(x)\).
• Si dos funciones son inversas, entonces cada una invertirá el efecto de la otra. Usando notación,\((f○g)(x)=f(g(x))=x\) y\((g○f)(x)=g(f(x))=x\).
• Las funciones inversas tienen notación especial. Si\(g\) es la inversa de\(f\), entonces podemos escribir\(g(x)=f^{-1}(x)\). Esta notación suele confundirse con exponentes negativos y no equivale a uno dividido por\(f(x)\).
• Las gráficas de inversas son simétricas alrededor de la línea\(y=x\). Si\((a,b)\) es un punto en la gráfica de una función, entonces\((b,a)\) es un punto en la gráfica de su inversa.
• Si cada punto en el rango de una función corresponde exactamente a un valor en el dominio, entonces la función es uno a uno. Utilice la prueba de línea horizontal para determinar si una función es o no de uno a uno.
• Una función uno a uno tiene una inversa, que a menudo se puede encontrar intercambiando\(x\) y\(y\), y resolviendo para\(y\). Esta nueva función es la inversa de la función original.

Ejercicio\(\PageIndex{3}\)

Dadas las funciones definidas por\(f\) y\(g\) find\((f \circ g)(x)\) y\((g \circ f)(x)\).

1. \(f(x)=4 x-1, g(x)=3 x\)
2. \(f(x)=-2 x+5, g(x)=2 x\)
3. \(f(x)=3 x-5, g(x)=x-4\)
4. \(f(x)=5 x+1, g(x)=2 x-3\)
5. \(f(x)=x^{2}-x+1, g(x)=2 x-1\)
6. \(f(x)=x^{2}-3 x-2, g(x)=x-2\)
7. \(f(x)=x^{2}+3, g(x)=x^{2}-5\)
8. \(f(x)=2 x^{2}, g(x)=x^{2}-x\)
9. \(f(x)=8 x^{3}+5, g(x)=\sqrt[3]{x-5}\)
10. \(f(x)=27 x^{3}-1, g(x)=\sqrt[3]{x+1}\)
11. \(f(x)=\frac{1}{x+5}, g(x)=\frac{1}{x}\)
12. \(f(x)=\frac{1}{x}-3, g(x)=\frac{3}{x+3}\)
13. \(f(x)=5 \sqrt{x}, g(x)=3 x-2\)
14. \(f(x)=\sqrt{2 x}, g(x)=4 x+1\)
15. \(f(x)=\frac{1}{2 x}, g(x)=x^{2}+8\)
16. \(f(x)=2 x-1, g(x)=\frac{1}{x+1}\)
17. \(f(x)=\frac{1-x}{2 x}, g(x)=\frac{1}{2 x+1}\)
18. \(f(x)=\frac{2 x}{x+1}, g(x)=\frac{x+1}{x}\)

Contestar

1. \((f \circ g)(x)=12 x-1 ;(g \circ f)(x)=12 x-3\)

3. \((f \circ g)(x)=3 x-17 ;(g \circ f)(x)=3 x-9\)

5. \((f \circ g)(x)=4 x^{2}-6 x+3 ;(g \circ f)(x)=2 x^{2}-2 x+1\)

7. \((f \circ g)(x)=x^{4}-10 x^{2}+28 ;(g \circ f)(x)=x^{4}+6 x^{2}+4\)

9. \((f \circ g)(x)=8 x-35 ;(g \circ f)(x)=2 x\)

11. \((f \circ g)(x)=\frac{x}{5 x+1} ;(g \circ f)(x)=x+5\)

13. \((f \circ g)(x)=5 \sqrt{3 x-2} ;(g \circ f)(x)=15 \sqrt{x}-2\)

15. \(\begin{array}{l}{(f \circ g)(x)=\frac{1}{2 x^{2}+16}}; {(g \circ f)(x)=\frac{1+32 x^{2}}{4 x^{2}}}\end{array}\)

17. \((f \circ g)(x)=x ;(g \circ f)(x)=x\)

Ejercicio\(\PageIndex{4}\)

Dadas las funciones definidas por\(f(x)=3 x^{2}-2, g(x)=5 x+1\), y\(h(x)=\sqrt{x}\), calcular lo siguiente.

1. \((f \circ g)(2)\)
2. \((g \circ f)(-1)\)
3. \((g \circ f)(0)\)
4. \((f \circ g)(0)\)
5. \((f \circ h)(3)\)
6. \((g \circ h)(16)\)
7. \((h \circ g)\left(\frac{3}{5}\right)\)
8. \((h \circ f)(-3)\)

Contestar

1. \(361\)

3. \(−9\)

5. \(7\)

7. \(2\)

Ejercicio\(\PageIndex{5}\)

Dadas las funciones definidas por\(f(x)=\sqrt[3]{x+3}, g(x)=8 x^{3}-3\), y\(h(x)=2 x-1\), calcular lo siguiente.

1. \(( f\circ g )(1)\)
2. \((g \circ f)(-2)\)
3. \((g \circ f)(0)\)
4. \((f \circ g)(-2)\)
5. \((f \circ h)(-1)\)
6. \((h \circ g)\left(-\frac{1}{2}\right)\)
7. \((h \circ f)(24)\)
8. \((g \circ h)(0)\)

Contestar

1. \(2\)

3. \(21\)

5. \(0\)

7. \(5\)

Ejercicio\(\PageIndex{6}\)

Dada la función, determinar\((f \circ f)(x)\).

1. \(f(x)=3 x-1\)
2. \(f(x)=\frac{2}{5} x+1\)
3. \(f(x)=x^{2}+5\)
4. \(f(x)=x^{2}-x+6\)
5. \(f(x)=x^{3}+2\)
6. \(f(x)=x^{3}-x\)
7. \(f(x)=\frac{1}{x+1}\)
8. \(f(x)=\frac{x+1}{2 x}\)

Contestar

1. \((f\circ f)(x)=9 x-4\)

3. \((f \circ f)(x)=x^{4}+10 x^{2}+30\)

5. \((f \circ f)(x)=x^{9}+6 x^{6}+12 x^{3}+10\)

7. \((f \circ f)(x)=\frac{x+1}{x+2}\)

Ejercicio\(\PageIndex{7}\)

¿Las funciones dadas son una a una? Explique.

1.

Figura\(\PageIndex{10}\)

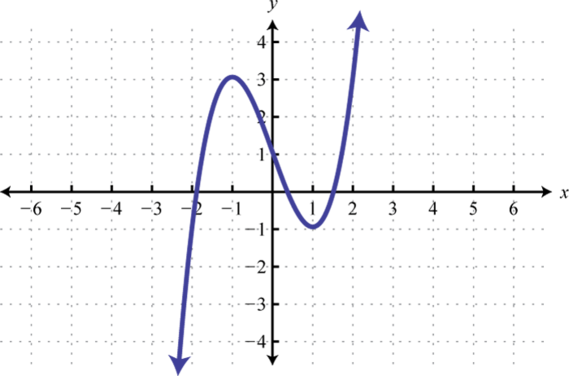
2.

Figura\(\PageIndex{11}\)

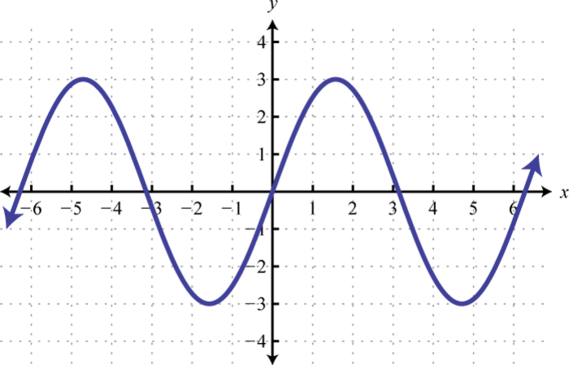
3.

Figura\(\PageIndex{12}\)

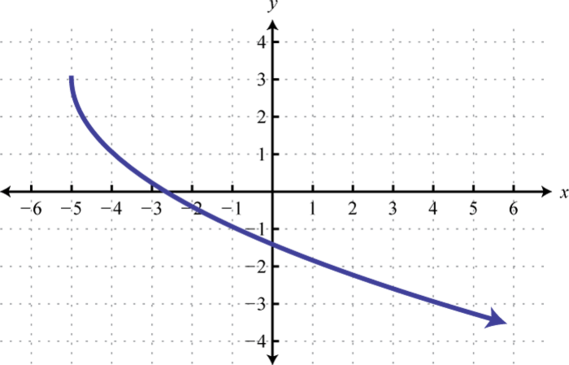
4.

Figura\(\PageIndex{13}\)

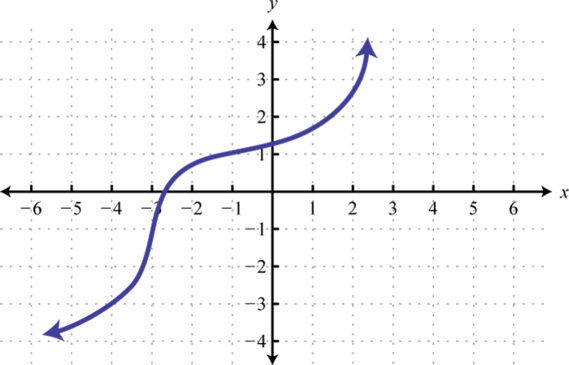
5. \(f(x)=x+1\)

6. \(g(x)=x^{2}+1\)

7. \(h(x)=|x|+1\)

8. \(r(x)=x^{3}+1\)

9. \(f(x)=\sqrt{x+1}\)

10. \(g(x)=3\)

Contestar

1. No, falla el HLT

3. Sí, pasa el HLT

5. Sí, su gráfica pasa el HLT.

7. No, su gráfica falla el HLT.

9. Sí, su gráfica pasa el HLT.

Ejercicio\(\PageIndex{8}\)

Dada la gráfica de una función uno a uno, graficar su inversa.

1.

Figura\(\PageIndex{14}\)

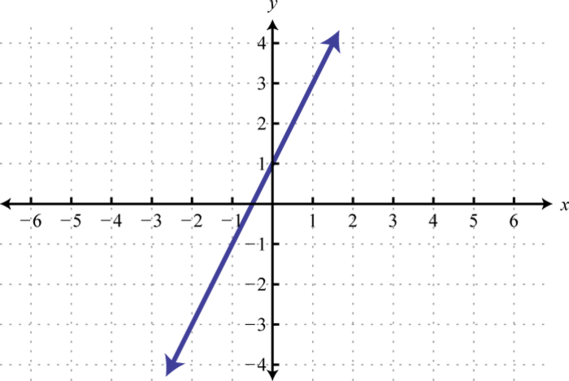
2.

Figura\(\PageIndex{15}\)

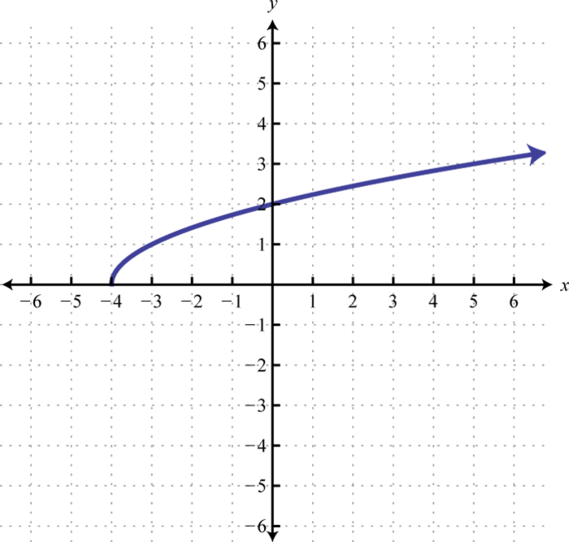
3.

Figura\(\PageIndex{16}\)

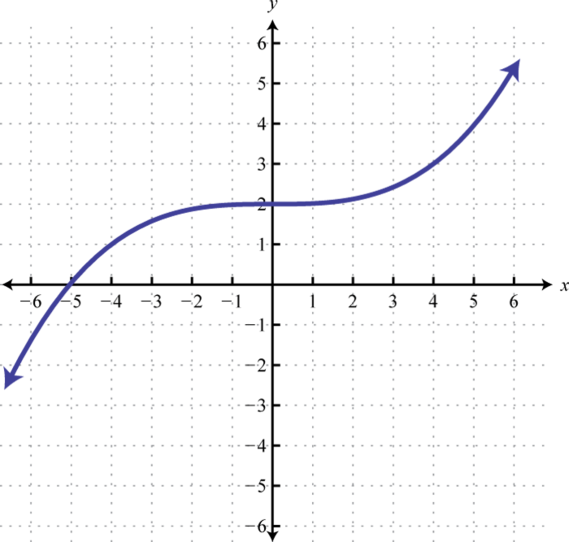
4.

Figura\(\PageIndex{17}\)

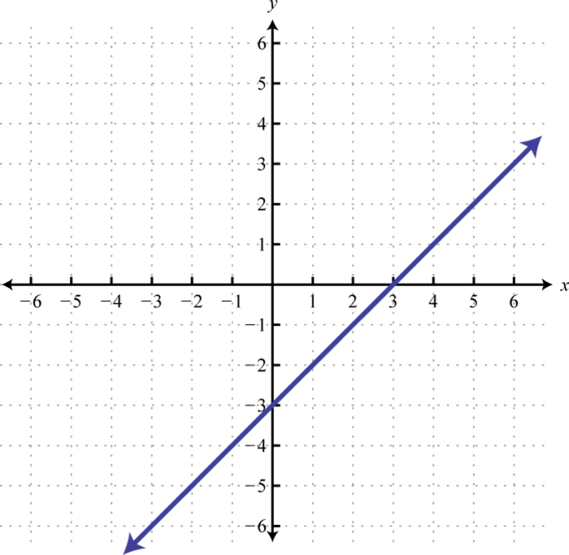
5.

Figura\(\PageIndex{18}\)

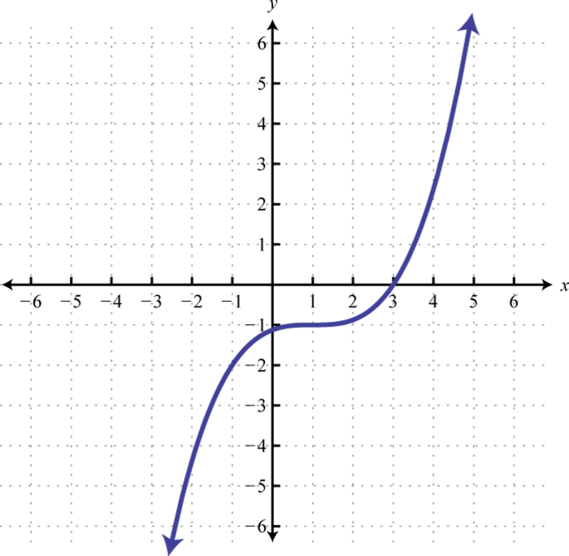
6.

Figura\(\PageIndex{19}\)

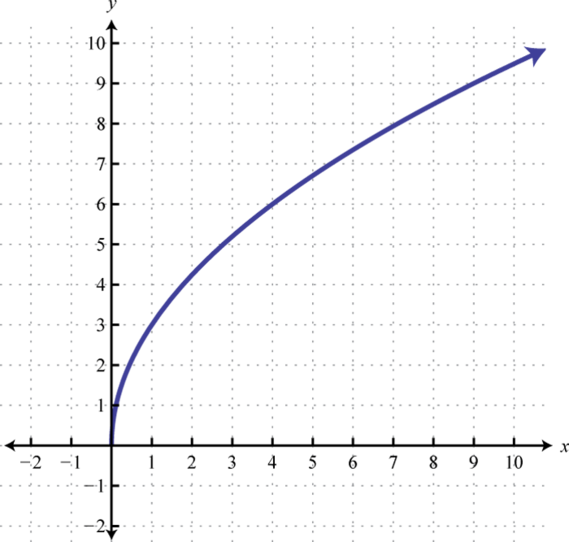
Contestar

1.

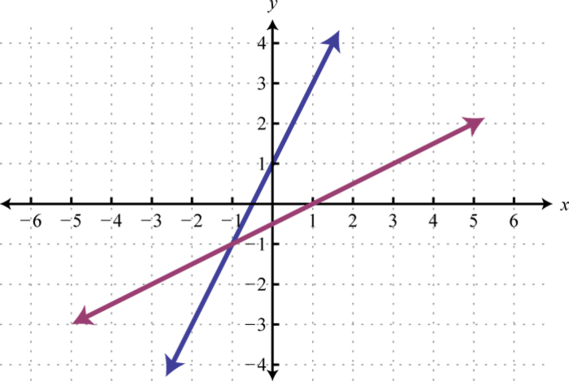
Figura\(\PageIndex{20}\)

3.

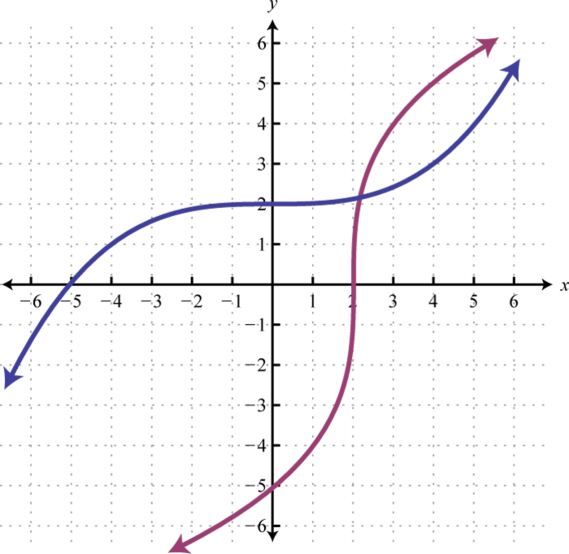
Figura\(\PageIndex{21}\)

5.

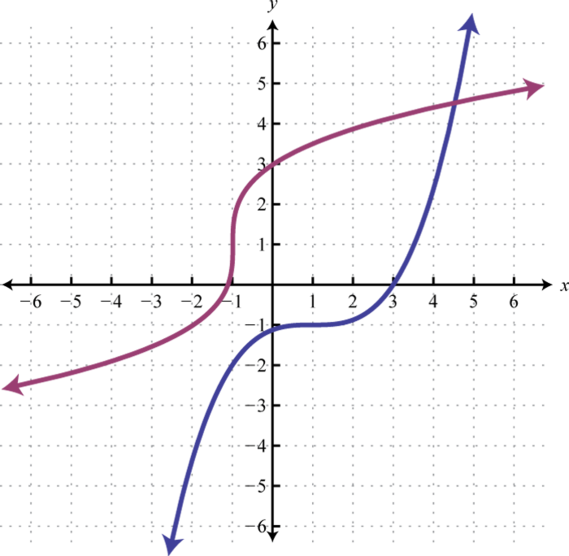
Figura\(\PageIndex{22}\)

Ejercicio\(\PageIndex{9}\)

Verificar algebraicamente que las dos funciones dadas son inversas. En otras palabras,\(\left(f \circ f^{-1}\right)(x)=x\) demuéstralo y\(\left(f^{-1} \circ f\right)(x)=x\).

1. \(f(x)=3 x-4, f^{-1}(x)=\frac{x+4}{3}\)
2. \(f(x)=-5 x+1, f^{-1}(x)=\frac{1-x}{5}\)
3. \(f(x)=-\frac{2}{3} x+1, f^{-1}(x)=-\frac{3}{2} x+\frac{3}{2}\)
4. \(f(x)=4 x-\frac{1}{3}, f^{-1}(x)=\frac{1}{4} x + \frac{1}{12}\)
5. \(f(x)=\sqrt{x-8}, f^{-1}(x)=x^{2}+8, x \geq 0\)
6. \(f(x)=\sqrt[3]{6 x}-3, f^{-1}(x)=\frac{(x+3)^{3}}{6}\)
7. \(f(x)=\frac{x}{x+1}, f^{-1}(x)=\frac{x}{1-x}\)
8. \(f(x)=\frac{x-3}{3 x}, f^{-1}(x)=\frac{3}{1-3 x}\)
9. \(f(x)=2(x-1)^{3}+3, f^{-1}(x)=1+\sqrt[3]{\frac{x-3}{2}}\)
10. \(f(x)=\sqrt[3]{5 x-1}+4, f^{-1}(x)=\frac{(x-4)^{3}+1}{5}\)

Contestar

1. Prueba

3. Prueba

5. Prueba

7. Prueba

9. Prueba

Ejercicio\(\PageIndex{10}\)

Encuentra las inversas de las siguientes funciones.

1. \(f(x)=5 x\)
2. \(f(x)=\frac{1}{2} x\)
3. \(f(x)=2 x+5\)
4. \(f(x)=-4 x+3\)
5. \(f(x)=-\frac{2}{3} x+\frac{1}{3}\)
6. \(f(x)=-\frac{1}{2} x+\frac{3}{4}\)
7. \(g(x)=x^{2}+5, x \geq 0\)
8. \(g(x)=x^{2}-7, x \geq 0\)
9. \(f(x)=(x-5)^{2}, x \geq 5\)
10. \(f(x)=(x+1)^{2}, x \geq-1\)
11. \(h(x)=3 x^{3}+5\)
12. \(h(x)=2 x^{3}-1\)
13. \(f(x)=(2 x-3)^{3}\)
14. \(f(x)=(x+4)^{3}-1\)
15. \(g(x)=\frac{2}{x^{3}+1}\)
16. \(g(x)=\frac{1}{x^{3}}-2\)
17. \(f(x)=\frac{5}{x+1}\)
18. \(f(x)=\frac{1}{2 x-9}\)
19. \(f(x)=\frac{x+5}{x-5}\)
20. \(f(x)=\frac{3 x-4}{2 x-1}\)
21. \(h(x)=\frac{x-5}{10 x}\)
22. \(h(x)=\frac{9 x+1}{3 x}\)
23. \(g(x)=\sqrt[3]{5 x+2}\)
24. \(g(x)=\sqrt[3]{4 x-3}\)
25. \(f(x)=\sqrt[3]{x-6}-4\)
26. \(f(x)=2 \sqrt[3]{x+2}+5\)
27. \(h(x)=\sqrt[5]{x+1}-3\)
28. \(h(x)=\sqrt[5]{x-8}+1\)
29. \(f(x)=m x+b, m \neq 0\)
30. \(f(x)=a x^{2}+c, x \geq 0\)
31. \(f(x)=a x^{3}+d\)
32. \(f(x)=a(x-h)^{2}+k, x \geq h\)

Contestar

1. \(f^{-1}(x)=\frac{x}{5}\)

3. \(f^{-1}(x)=\frac{1}{2} x-\frac{5}{2}\)

5. \(f^{-1}(x)=-\frac{3}{2} x+\frac{1}{2}\)

7. \(g^{-1}(x)=\sqrt{x-5}\)

9. \(f^{-1}(x)=\sqrt{x}+5\)

11. \(h^{-1}(x)=\sqrt[3]{\frac{x-5}{3}}\)

13. \(f^{-1}(x)=\frac{\sqrt[3]{x}+3}{2}\)

15. \(g^{-1}(x)=\sqrt[3]{\frac{2-x}{x}}\)

17. \(f^{-1}(x)=\frac{5-x}{x}\)

19. \(f^{-1}(x)=\frac{5(x+1)}{x-1}\)

21. \(h^{-1}(x)=-\frac{5}{10 x-1}\)

23. \(g^{-1}(x)=\frac{x^{3}-2}{5}\)

25. \(f^{-1}(x)=(x+4)^{3}+6\)

27. \(h^{-1}(x)=(x+3)^{5}-1\)

29. \(f^{-1}(x)=\frac{x-b}{m}\)

31. \(f^{-1}(x)=\sqrt[3]{\frac{x-d}{a}}\)

Ejercicio\(\PageIndex{11}\)

Grafica la función y su inversa en el mismo conjunto de ejes.

1. \(f(x)=x+2\)
2. \(f(x)=\frac{2}{3} x-4\)
3. \(f(x)=-2 x+2\)
4. \(f(x)=-\frac{1}{3} x+4\)
5. \(g(x)=x^{2}-2, x \geq 0\)
6. \(g(x)=(x-2)^{2}, x \geq 2\)
7. \(h(x)=x^{3}+1\)
8. \(h(x)=(x+2)^{3}-2\)
9. \(f(x)=2-\sqrt{x}\)
10. \(f(x)=\sqrt{-x}+1\)

Contestar

1.

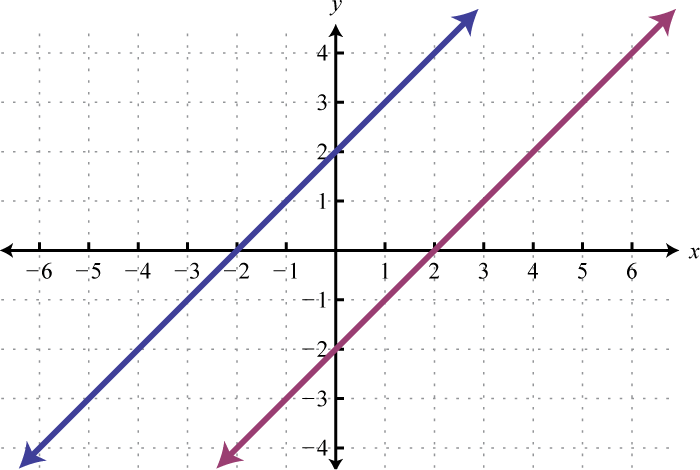
Figura\(\PageIndex{23}\)

3.

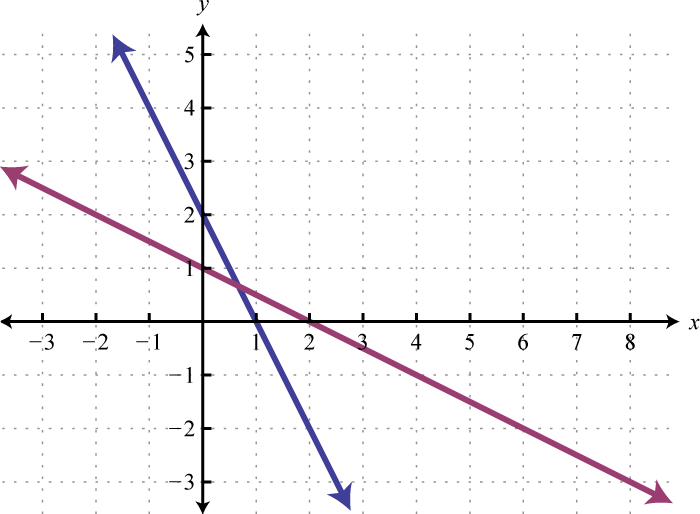
Figura\(\PageIndex{24}\)

5.

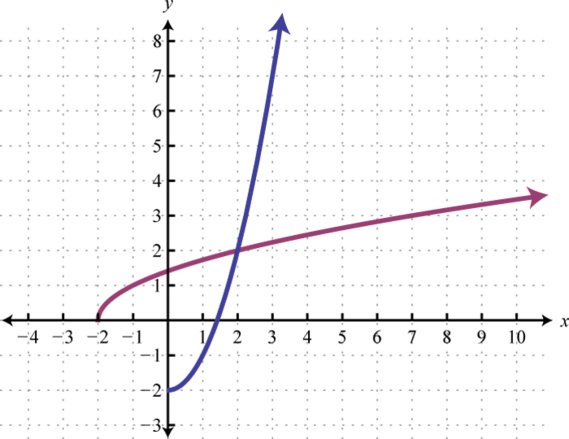
Figura\(\PageIndex{25}\)

7.

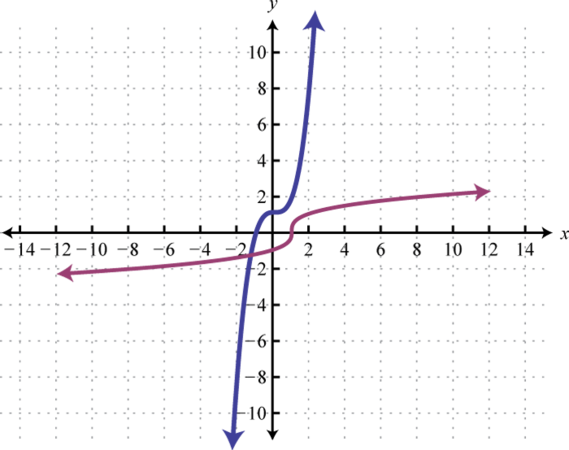
Figura\(\PageIndex{26}\)

9.

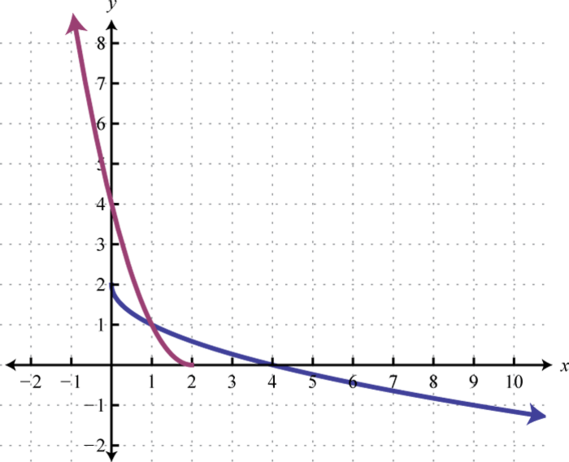
Figura\(\PageIndex{27}\)

Ejercicio\(\PageIndex{12}\)

1. ¿La composición de las funciones es asociativa? Explique.
2. Explicar por qué\(C(x)=\frac{5}{9}(x-32)\) y\(F(x)=\frac{9}{5} x+32\) definir funciones inversas. Demostrarlo algebraicamente.
3. ¿Las gráficas de todas las líneas rectas representan funciones uno a uno? Explique.
4. Si las gráficas de las funciones inversas se cruzan, entonces ¿cómo podemos encontrar el punto de intersección? Explique.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

¹ Aplicar una función a los resultados de otra función.

² El punto abierto utilizado para indicar la composición de la función\((f ○g) (x) = f (g (x))\)

³ Funciones donde cada valor en el rango corresponde exactamente a un valor en el dominio.

⁴ Si una línea horizontal cruza la gráfica de una función más de una vez, entonces no es uno a uno.

.