7.2: Funciones exponenciales y sus gráficas
- Page ID
- 109862
Objetivos de aprendizaje
- Identificar y evaluar funciones exponenciales.
- Esbozar la gráfica de funciones exponenciales y determinar el dominio y el rango.
- Identificar y graficar la función exponencial natural.
- Aplicar las fórmulas para interés compuesto.
Funciones exponenciales
En este punto de nuestro estudio del álgebra comenzamos a observar funciones trascendentales o funciones que parecen “trascender” el álgebra. Hemos estudiado funciones con bases variables y exponentes constantes como\(x^{2}\) o\(y^{−3}\). En esta sección exploramos funciones con una base constante y exponentes variables. Dado un número real\(b > 0\) donde\(b ≠ 1\) una función exponencial 5 tiene la forma,
\(f(x)=b^{x} \quad \color{Cerulean}{Exponential\:Function}\)
Por ejemplo, si la base\(b\) es igual a\(2\), entonces tenemos la función exponencial definida por\(f (x) = 2^{x}\). Aquí podemos ver que el exponente es la variable. Hasta este punto, se han definido exponentes racionales pero exponentes irracionales no. Consideremos\(2^{\sqrt{7}}\), donde el exponente es un número irracional en el rango,
\(2.64<\sqrt{7}<2.65\)
Podemos usar estos límites para estimar\(2^{\sqrt{7}}\),
\(2^{2.64}<2^{\sqrt{7}}<2^{2.65}\)
\(6.23<2^{\sqrt{7}}<6.28\)
Usando exponentes racionales de esta manera, se\(2^{\sqrt{7}}\) puede obtener una aproximación de a cualquier nivel de precisión. En una calculadora,
\(2^{\wedge} \sqrt{7} \approx 6.26\)
Por lo tanto, el dominio de cualquier función exponencial consiste en todos los números reales\((−∞, ∞)\). Elija algunos valores para\(x\) y luego determine los\(y\) valores -correspondientes.
| \(x\) | \(y\) | \(f(x)=2^{x}\) | \(\color{Cerulean}{Solutions}\) |
|---|---|---|---|
| \ (x\) ">\(-2\) | \ (y\) ">\(\color{Cerulean}{\frac{1}{4}}\) | \ (f (x) =2^ {x}\) ">\(y=2^{-2}=\frac{1}{2^{2}}=\frac{1}{4}\) | \ (\ color {cerúleo} {Soluciones}\) ">\(\left(-2, \frac{1}{4}\right)\) |
| \ (x\) ">\(-1\) | \ (y\) ">\(\color{Cerulean}{\frac{1}{2}}\) | \ (f (x) =2^ {x}\) ">\(y=2^{-1}=\frac{1}{2^{1}}=\frac{1}{2}\) | \ (\ color {cerúleo} {Soluciones}\) ">\(\left(-1, \frac{1}{2}\right)\) |
| \ (x\) ">\(0\) | \ (y\) ">\(\color{Cerulean}{1} \) | \ (f (x) =2^ {x}\) ">\(y=2^{0}=1\) | \ (\ color {cerúleo} {Soluciones}\) ">\((0,1)\) |
| \ (x\) ">\(1\) | \ (y\) ">\(\color{Cerulean}{2}\) | \ (f (x) =2^ {x}\) ">\(y=2^{1}=2\) | \ (\ color {cerúleo} {Soluciones}\) ">\((1,2)\) |
| \ (x\) ">\(2\) | \ (y\) ">\(\color{Cerulean}{4}\) | \ (f (x) =2^ {x}\) ">\(y=2^{2}=4\) | \ (\ color {cerúleo} {Soluciones}\) ">\((2,4)\) |
| \ (x\) ">\(\sqrt{7}\) | \ (y\) ">\(\color{Cerulean}{6.26}\) | \ (f (x) =2^ {x}\) ">\(y=2^{\sqrt{7}} \approx 6.26\) | \ (\ color {cerúleo} {Soluciones}\) ">\((2.65,6.26)\) |
Debido a que los exponentes están definidos para cualquier número real, podemos esbozar la gráfica usando una curva continua a través de estos puntos dados:
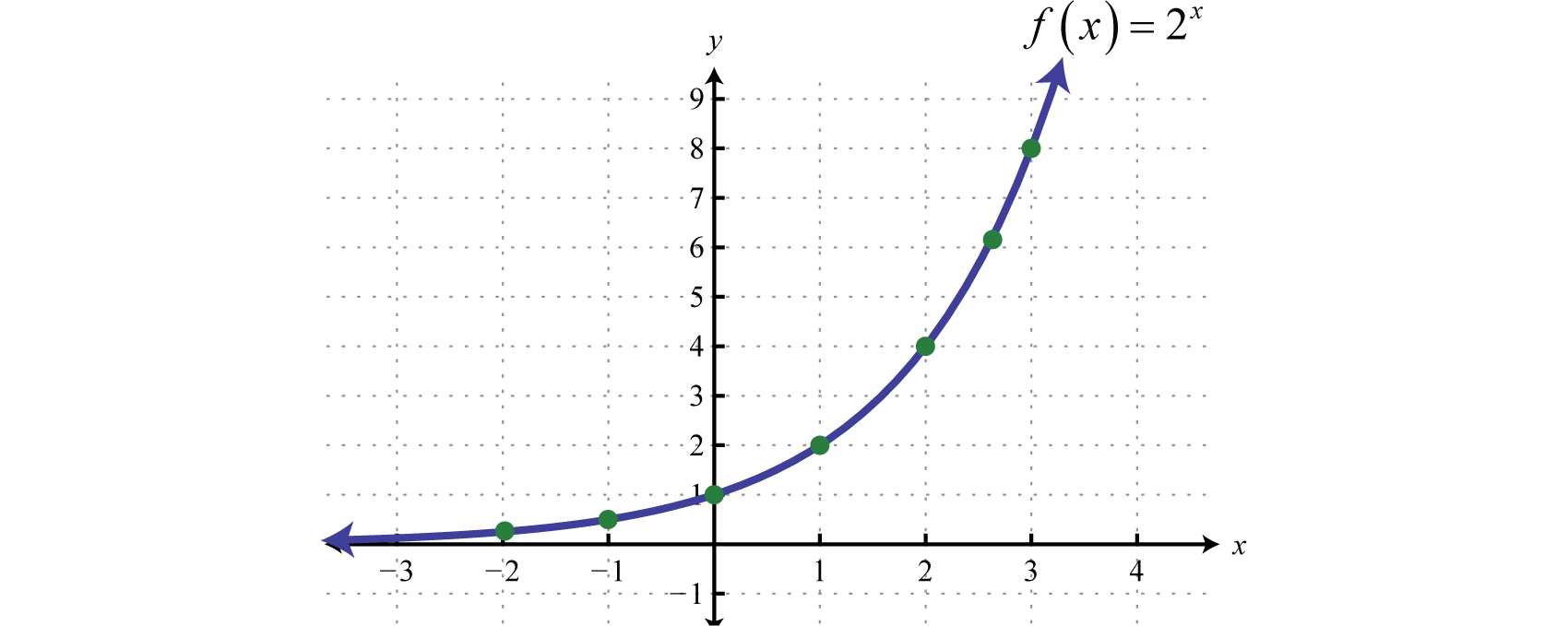
Es importante señalar que a medida que se\(x\) acerca al infinito negativo, los resultados se vuelven muy pequeños pero nunca alcanzan realmente cero. Por ejemplo,
\(f(-5)=2^{-5}=\frac{1}{2^{5}} \approx 0.03125\)
\(f(-10)=2^{-10}=\frac{1}{2^{10}} \approx 0.0009766\)
\(f(-15)=2^{-15}=\frac{1}{2^{-15}} \approx .00003052\)
Esto describe una asíntota horizontal en\(y = 0\), el\(x\) eje, y define un límite inferior para el rango de la función:\((0, ∞)\).
La base\(b\) de una función exponencial afecta la velocidad a la que crece. A continuación hemos graficado\(y = 2^{x} , y = 3^{x}\), y\(y = 10^{x}\) en el mismo conjunto de ejes.
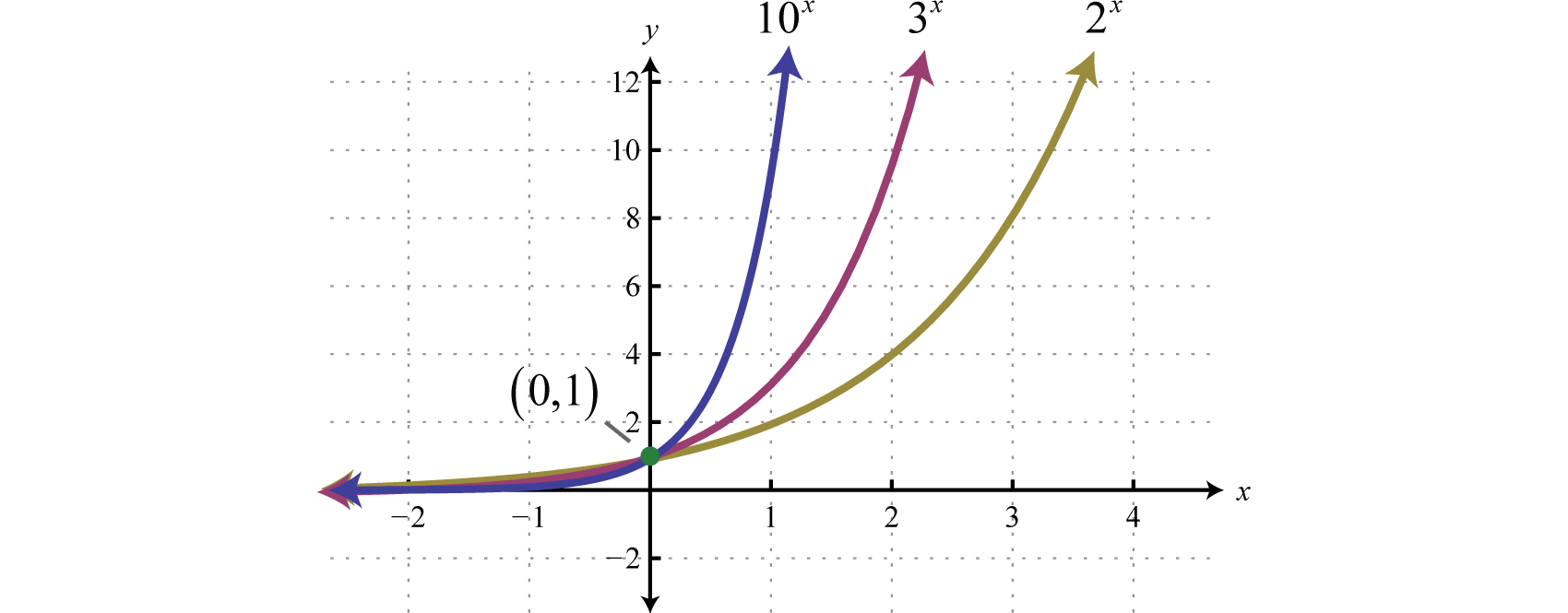
Tenga en cuenta que todas estas funciones exponenciales tienen la misma\(y\) -intercepción, es decir\((0, 1)\). Esto se debe a que\(f (0) = b^{0} = 1\) para cualquier función definida usando el formulario\(f (x) = b^{x}\). A medida que las funciones se leen de izquierda a derecha, se interpretan como crecientes o creciendo exponencialmente. Además, cualquier función exponencial de esta forma tendrá un dominio que consiste en todos los números reales\((−∞, ∞)\) y un rango que consiste en valores positivos\((0, ∞)\) delimitados por una asíntota horizontal en\(y = 0\).
Ejemplo\(\PageIndex{1}\):
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=10^{x}+5\).
Solución
La base\(10\) se utiliza a menudo, sobre todo con notación científica. De ahí\(10\) que se llame la base común. De hecho, la función exponencial\(y = 10^{x}\) es tan importante que encontrarás un botón\(10^{x}\) dedicado a ella en la mayoría de las calculadoras científicas modernas. En este ejemplo, esbozaremos la gráfica básica\(y = 10^{x}\) y luego la desplazaremos hacia arriba\(5\) las unidades.
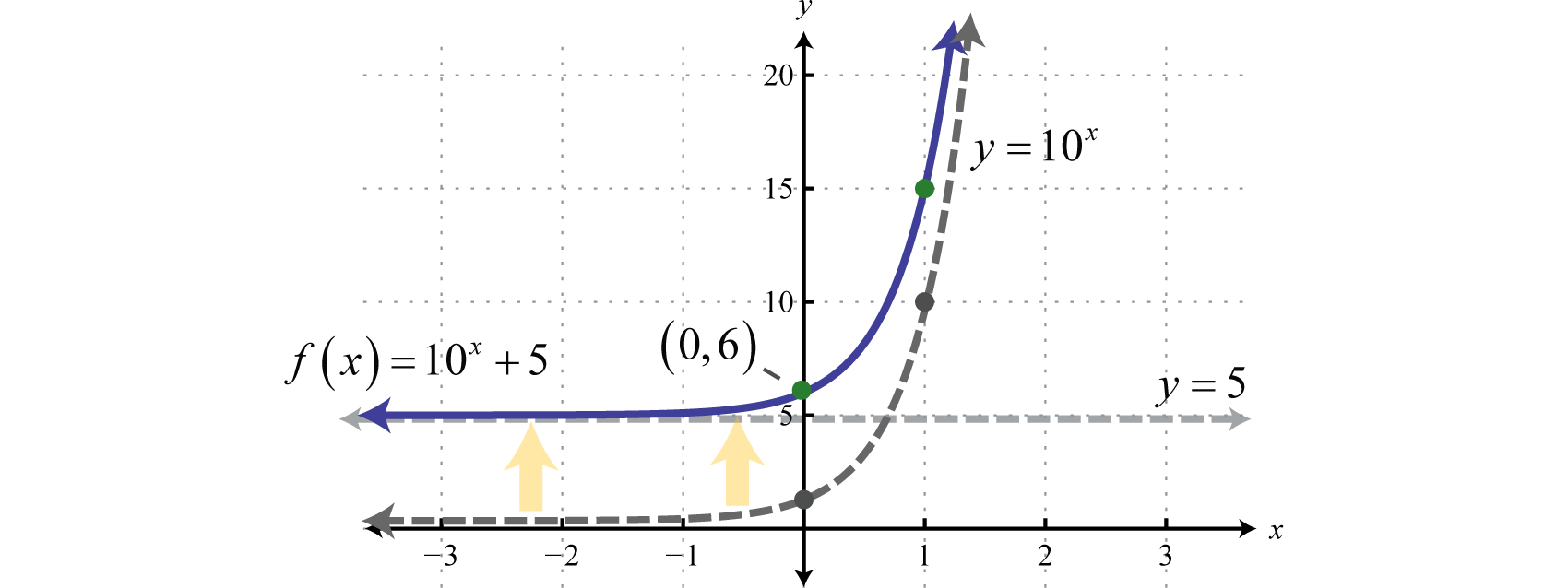
Obsérvese que la asíntota horizontal de la gráfica básica\(y = 10^{x}\) se desplazó hacia arriba\(5\) unidades hasta\(y = 5\) (se muestra discontinua). Tómese un minuto para evaluar algunos valores de\(x\) con su calculadora y convencerse de que el resultado nunca será menor que\(5\).
Contestar
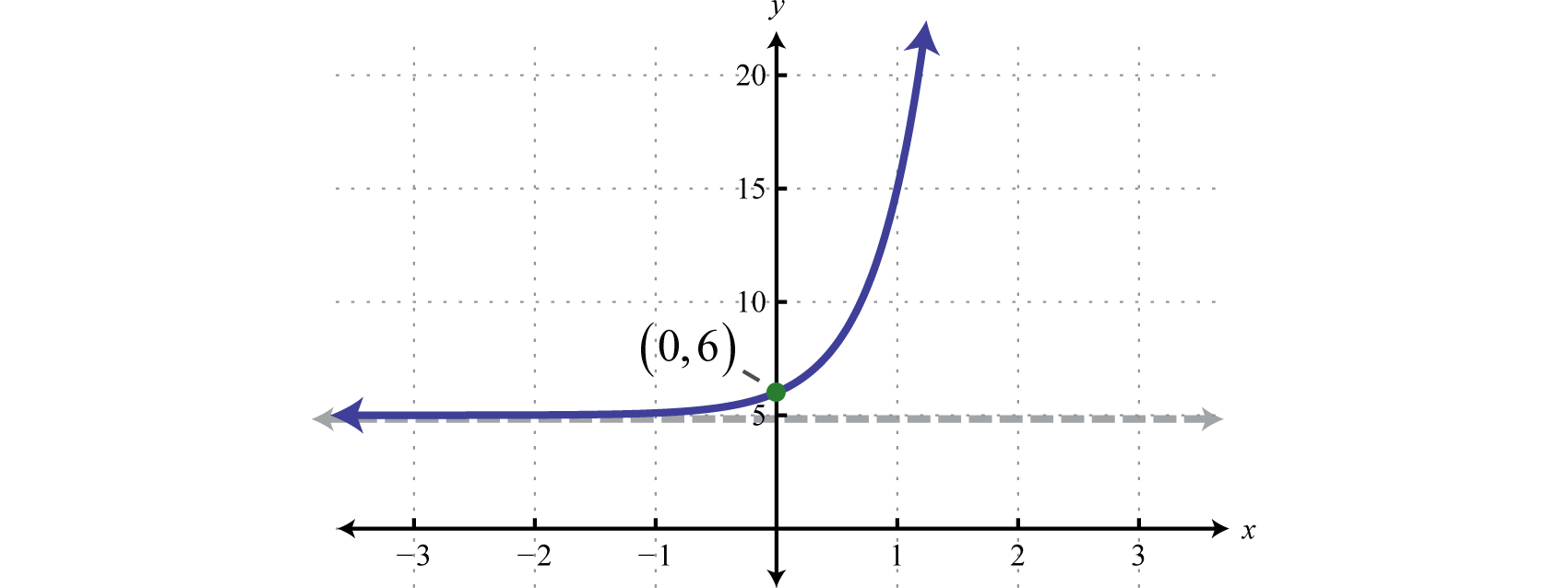
Dominio:\((-\infty, \infty)\); Rango:\((5, \infty)\)
A continuación considere funciones exponenciales con bases fraccionarias\(0 < b < 1\). Por ejemplo,\(f(x)=\left(\frac{1}{2}\right)^{x}\) es una función exponencial con base\(b = \frac{1}{2}\).
| \(x\) | \(y\) | \(f(x)=\left(\frac{1}{2}\right)^{x}\) | \(\color{Cerulean}{Solutions} \) |
|---|---|---|---|
| \ (x\)” style="vertical-align:middle; ">\(-2\) | \ (y\)” style="vertical-align:middle; ">\(\color{Cerulean}{4} \) | \ (f (x) =\ izquierda (\ frac {1} {2}\ derecha) ^ {x}\)” style="vertical-align:middle; ">\(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{-2}=\frac{1^{-2}}{2^{-2}}=\frac{2^{2}}{1^{2}}=4\) | \ (\ color {cerúleo} {Soluciones}\)” style="vertical-align:middle; ">\((-2,4)\) |
| \ (x\)” style="vertical-align:middle; ">\(-1\) | \ (y\)” style="vertical-align:middle; ">\(\color{Cerulean}{2}\) | \ (f (x) =\ izquierda (\ frac {1} {2}\ derecha) ^ {x}\)” style="vertical-align:middle; ">\(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{-1}=\frac{1^{-1}}{2^{-1}}=\frac{2^{1}}{1^{1}}=2\) | \ (\ color {cerúleo} {Soluciones}\)” style="vertical-align:middle; ">\((-1,2)\) |
| \ (x\)” style="vertical-align:middle; ">\(0\) | \ (y\)” style="vertical-align:middle; ">\(\color{Cerulean}{1}\) | \ (f (x) =\ izquierda (\ frac {1} {2}\ derecha) ^ {x}\)” style="vertical-align:middle; ">\(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{0}=1\) | \ (\ color {cerúleo} {Soluciones}\)” style="vertical-align:middle; ">\((0,1)\) |
| \ (x\)” style="vertical-align:middle; ">\(1\) | \ (y\)” style="vertical-align:middle; ">\(\color{Cerulean}{\frac{1}{2}}\) | \ (f (x) =\ izquierda (\ frac {1} {2}\ derecha) ^ {x}\)” style="vertical-align:middle; ">\(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{1}=\frac{1}{2}\) | \ (\ color {cerúleo} {Soluciones}\)” style="vertical-align:middle; ">\(\left(1, \frac{1}{2}\right)\) |
| \ (x\)” style="vertical-align:middle; ">\(2\) | \ (y\)” style="vertical-align:middle; ">\(\color{Cerulean}{\frac{1}{4}}\) | \ (f (x) =\ izquierda (\ frac {1} {2}\ derecha) ^ {x}\)” style="vertical-align:middle; ">\(f\left(\frac{1}{2}\right)=\left(\frac{1}{2}\right)^{2}=\frac{1}{4}\) | \ (\ color {cerúleo} {Soluciones}\)” style="vertical-align:middle; ">\(\left(2, \frac{1}{4}\right)\) |
Puntos de trazado que tenemos,
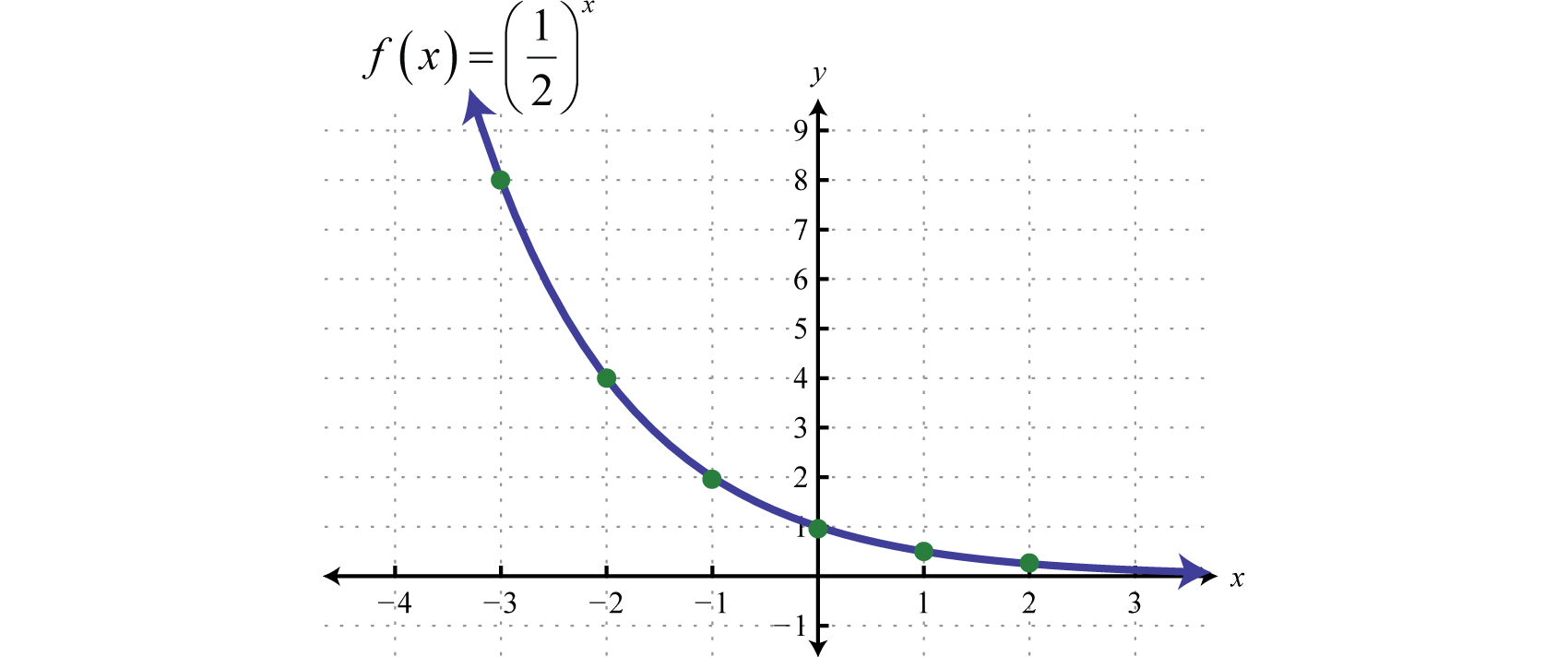
Al leer la gráfica de izquierda a derecha, se interpreta como decreciente exponencialmente. La base afecta la velocidad a la que la función exponencial disminuye o decae. A continuación hemos graficado\(y=\left(\frac{1}{2}\right)^{x}, y=\left(\frac{1}{3}\right)^{x}\), y\(y=\left(\frac{1}{10}\right)^{x}\) en el mismo conjunto de ejes.
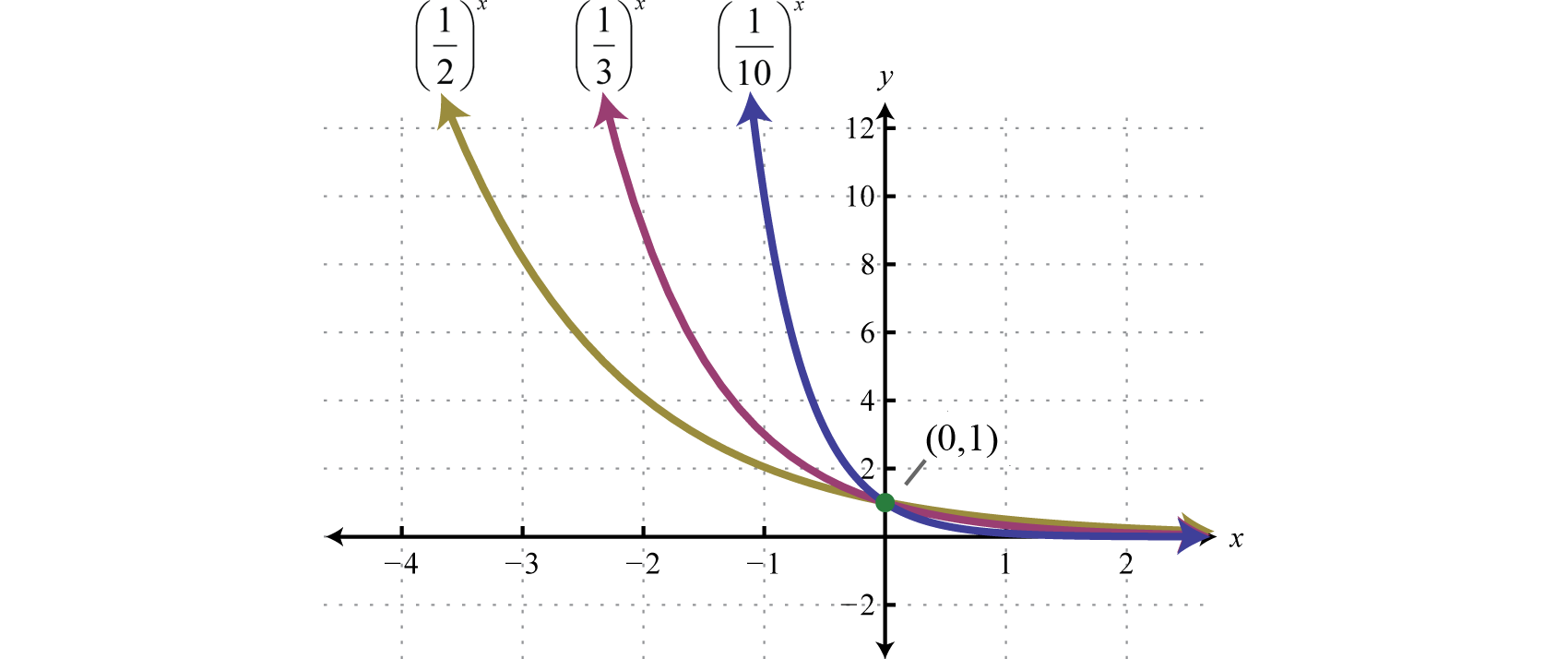
Recordemos eso\(x^{-1}=\frac{1}{x}\) y así podemos expresar funciones exponenciales con bases fraccionarias usando exponentes negativos. Por ejemplo,
\(g(x)=\left(\frac{1}{2}\right)^{x}=\frac{1^{x}}{2^{x}}=\frac{1}{2^{x}}=2^{-x}\)
Además, dado que\(f (x) = 2^{x}\) podemos ver\(g(x)=f(-x)=2^{-x}\) y podemos\(g\) considerar como un reflejo de\(f\) alrededor del\(y\) eje.
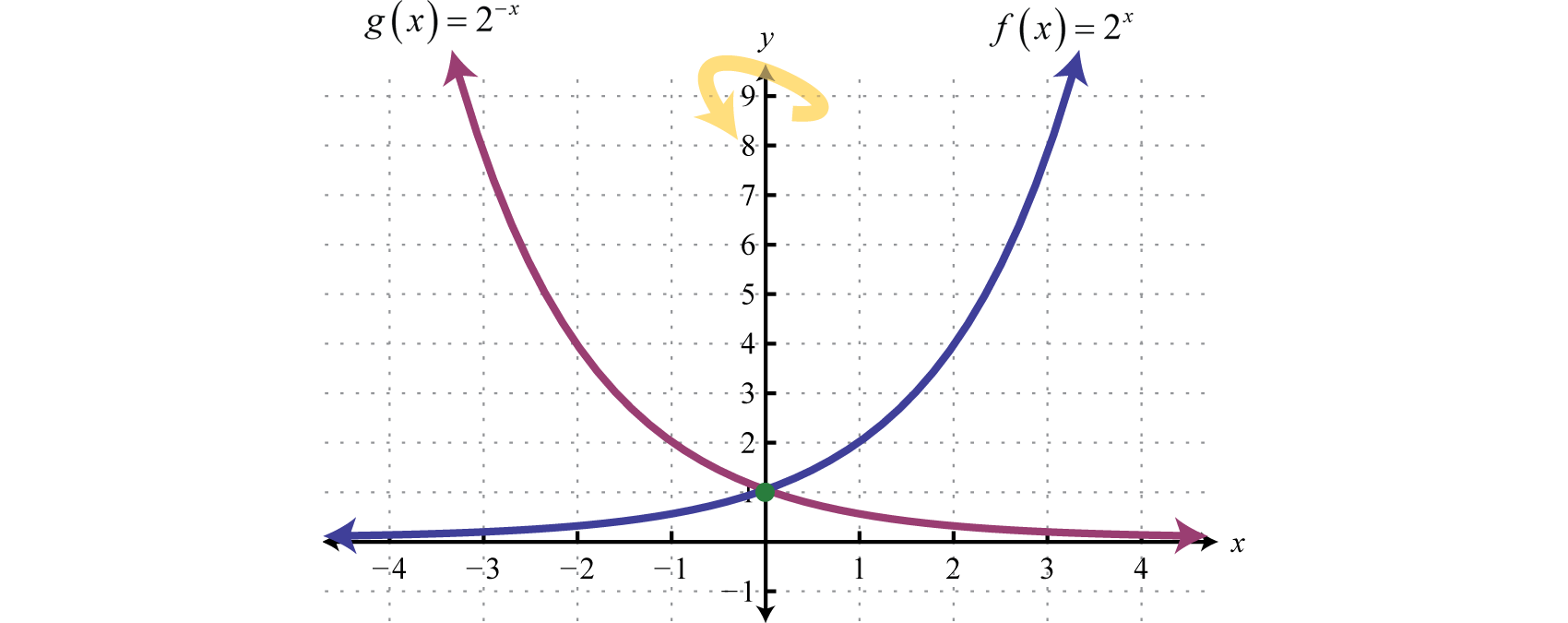
En resumen, dado\(b > 0\)
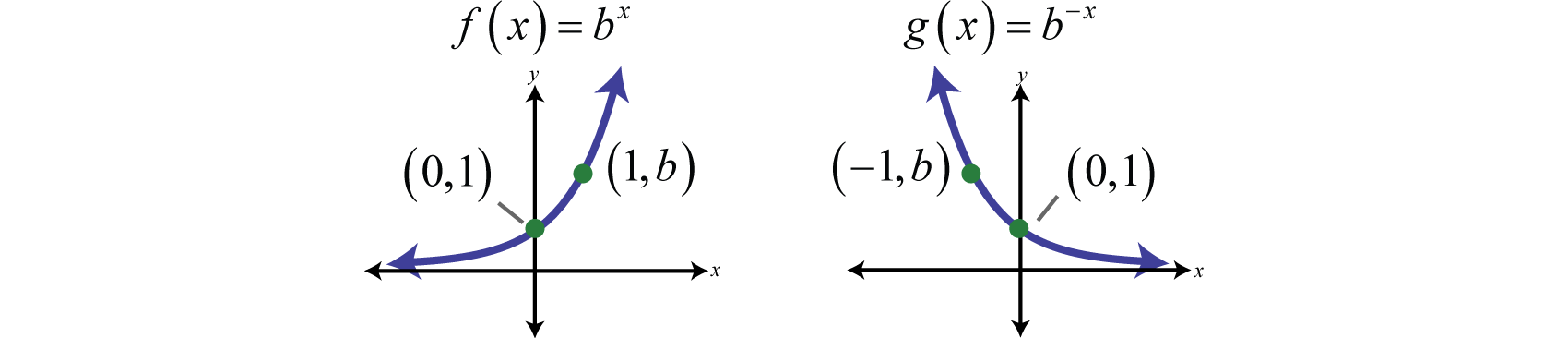
Y para ambos casos,
\(\begin{aligned}\color{Cerulean} { Domain :}&(-\infty, \infty) \\ \color{Cerulean} { Range : }&(0, \infty) \\ \color{Cerulean} { y-intercept : }&(0,1) \\ \color{Cerulean} { Asymptote: }& y=0\end{aligned}\)
Además, tenga en cuenta que las gráficas pasan la prueba de líneas horizontales y, por lo tanto, las funciones exponenciales son uno a uno. Utilizamos estas gráficas básicas, junto con las transformaciones, para bosquejar las gráficas de funciones exponenciales.
Ejemplo\(\PageIndex{2}\)
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=5^{-x}-10\).
Solución
Comienza con la gráfica básica\(y = 5^{−x}\) y desplázala hacia abajo\(10\) unidades.
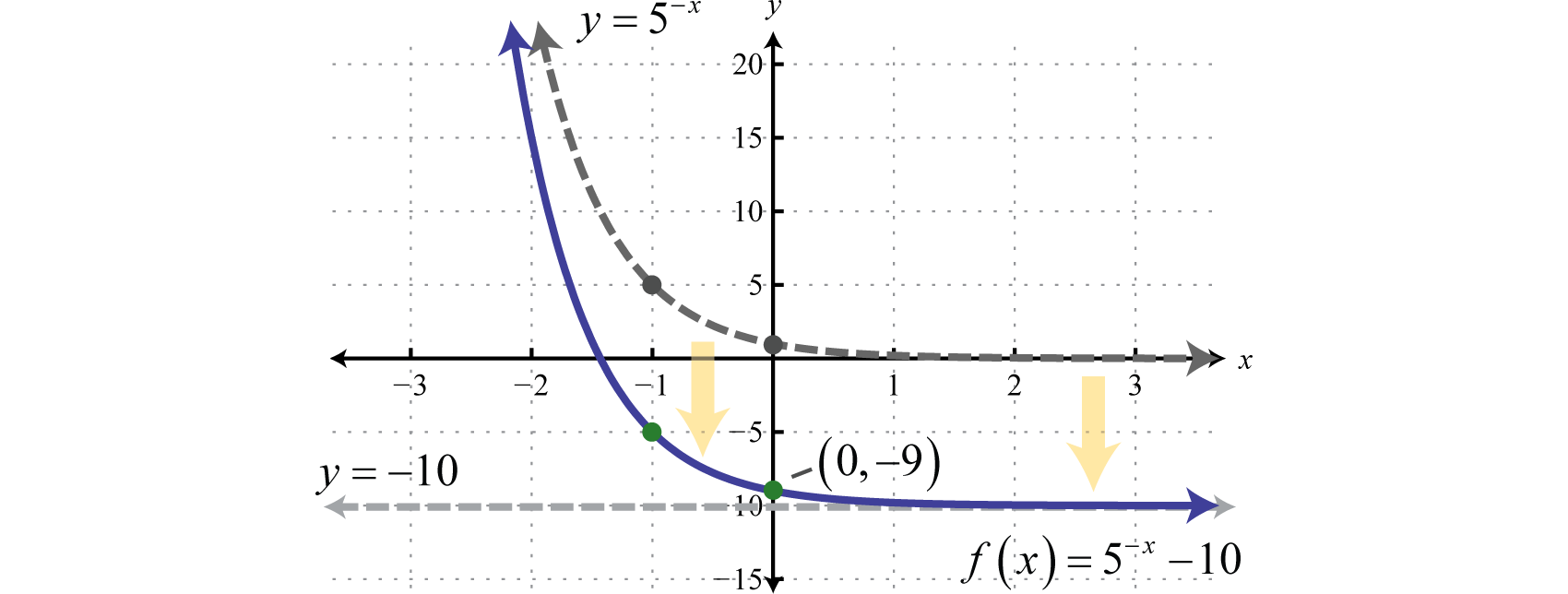
La\(y\) -intercepción es\((0, −9)\) y la asíntota horizontal es\(y = −10\).
Contestar
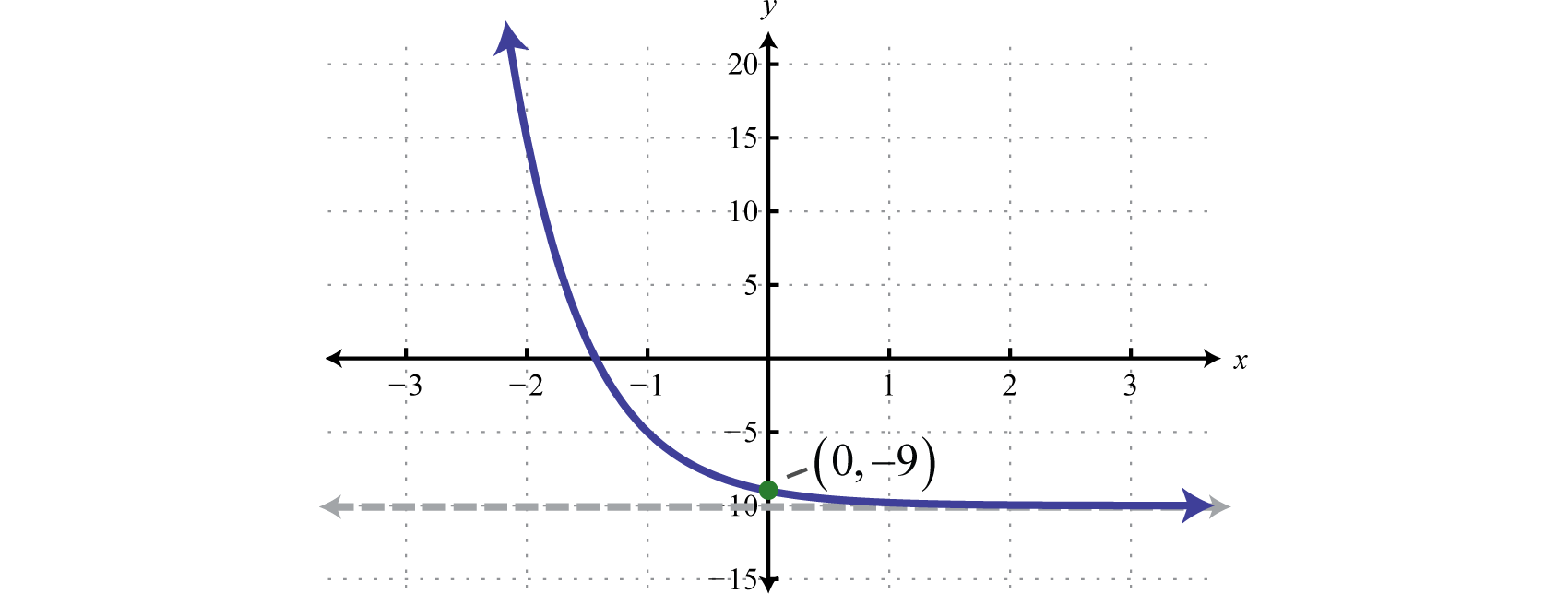
Dominio:\((-\infty, \infty)\); Rango:\((-10, \infty)\)
Encontrar la\(x\) -intercepción de la gráfica en el ejemplo anterior se deja para una sección posterior en este capítulo. Por ahora, nos preocupa más la forma general de las funciones exponenciales.
Ejemplo\(\PageIndex{3}\)
Dibuje la gráfica y determine el dominio y rango de\(g(x)=-2^{x-3}\).
Solución
Comience con la gráfica básica\(y=2^{x}\) e identifique las transformaciones.
\(\begin{array}{l}{y=2^{x}} \quad\quad\quad\color{Cerulean}{Basic\:graph} \\ {y=-2^{x}} \quad\:\:\:\:\color{Cerulean}{Reflection\:about\:the\:x-axis} \\ {y=-2^{x-3}}\quad\color{Cerulean}{Shift\:right\:3\:units}\end{array}\)
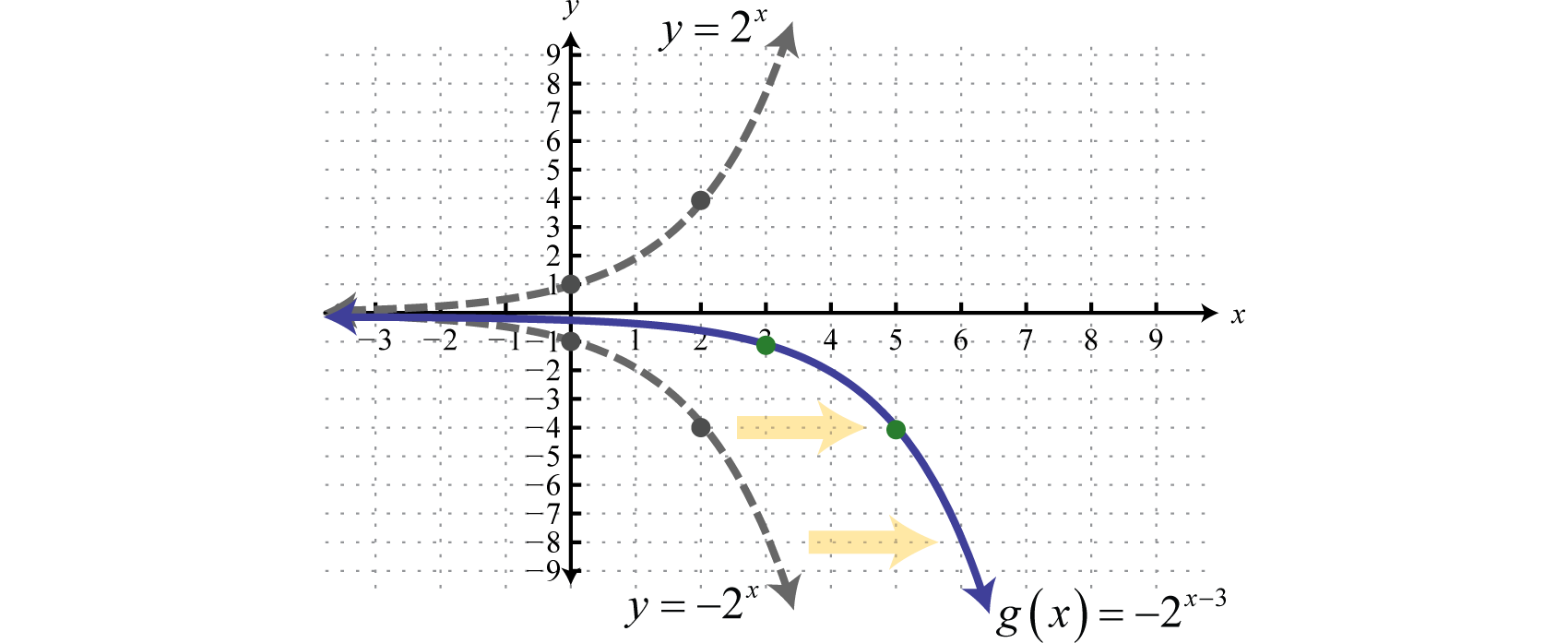
Tenga en cuenta que la asíntota horizontal permanece igual para todas las transformaciones. Para terminar solemos querer incluir la\(y\) -intercepción. Recuerda eso para encontrar la\(y\) -intercepción que establecemos\(x = 0\).
\(\begin{aligned} g(\color{Cerulean}{0}\color{black}{)} &=-2^{\color{Cerulean}{0}\color{black}{-}3} \\ &=-2^{-3} \\ &=-\frac{1}{2^{3}} \\ &=-\frac{1}{8} \end{aligned}\)
Por lo tanto la\(y\) -intercepción es\(\left(0,-\frac{1}{8}\right)\).
Contestar
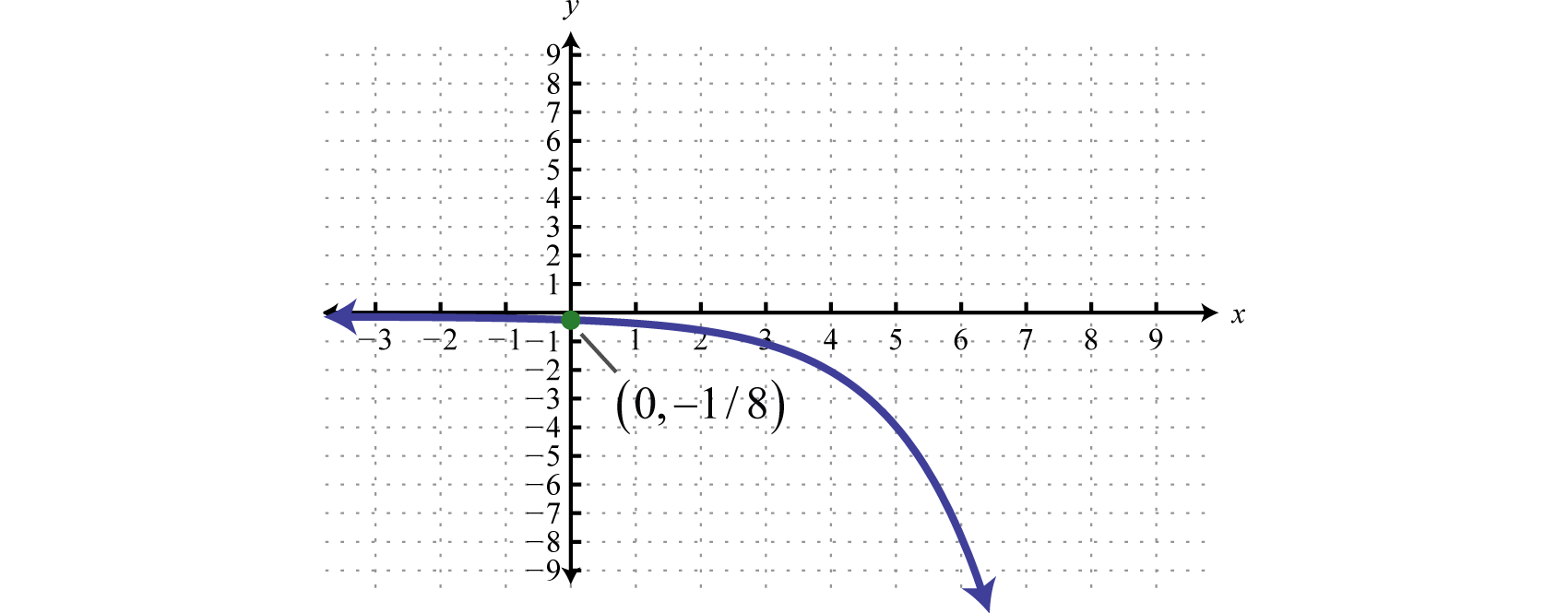
Dominio:\((-\infty, \infty)\); Rango:\((-\infty, 0)\)
Ejercicio\(\PageIndex{1}\)
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=2^{x-1}+3\)
- Contestar
-
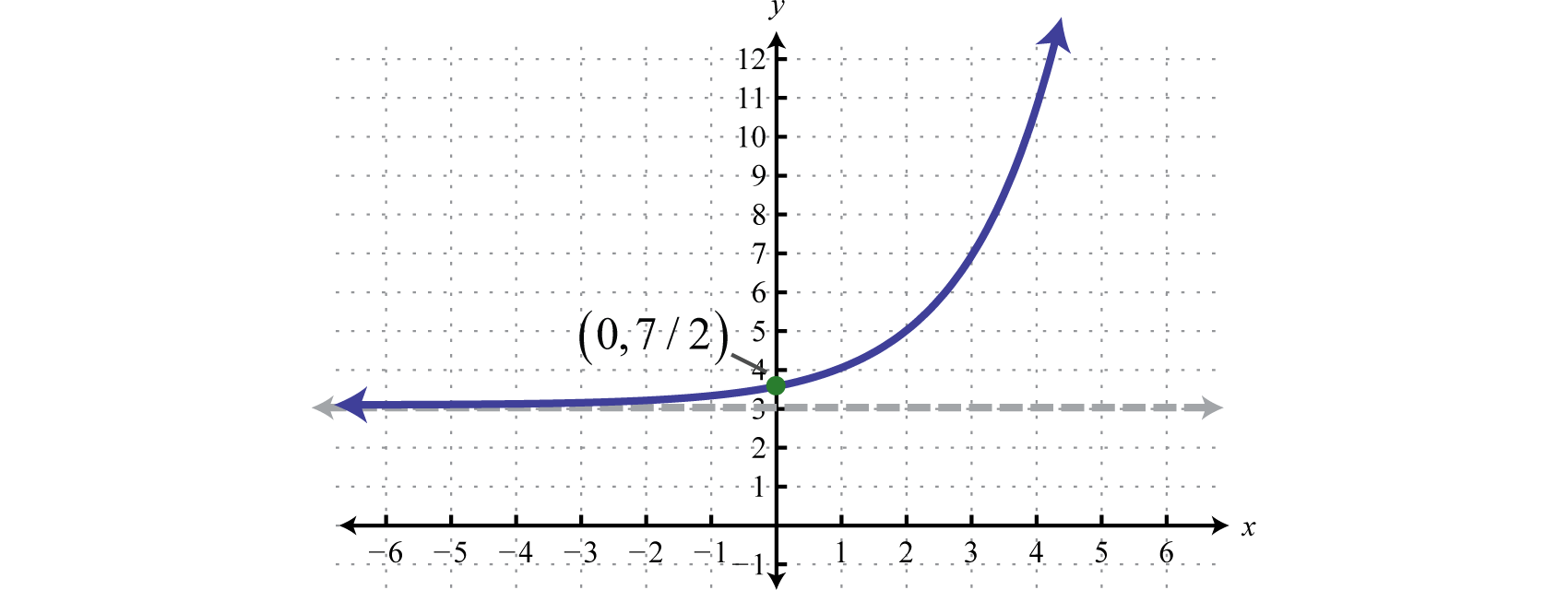
Figura\(\PageIndex{13}\) Dominio:\((-\infty, \infty)\); Rango:\((3, \infty)\)
www.youtube.com/v/wdcobqdte7m
Base Natural e
Algunos números ocurren a menudo en aplicaciones comunes. Uno de esos números familiares es pi (\(π\)), que sabemos que ocurre cuando se trabaja con círculos. Este número irracional tiene un botón dedicado en la mayoría de las calculadoras\(π\) y aproximado a cinco decimales,\(π ≈ 3.14159\). Otro número importante\(e\) ocurre cuando se trabaja con modelos exponenciales de crecimiento y decaimiento. Se trata de un número irracional y aproximado a cinco decimales,\(e ≈ 2.71828\). Esta constante ocurre naturalmente en muchas aplicaciones del mundo real y así se llama la base natural. A veces\(e\) se llama la constante de Euler en honor a Leonhard Euler (pronunciado “Oiler”).

Figura\(\PageIndex{14}\): Leonhard Euler (1707-1783)
De hecho, la función exponencial natural:
\(f(x)=e^{x}\)
es tan importante que encontrarás un botón\(e^{x}\) dedicado a ello en cualquier calculadora científica moderna. En esta sección, nos interesa evaluar la función exponencial natural para números reales dados y esbozar su gráfica. Para evaluar la función exponencial natural, definida por\(f (x) = e^{x}\) donde se\(x = −2\) usa una calculadora, es posible que deba aplicar el botón shift. En muchas calculadoras científicas el caret se mostrará de la siguiente manera,
\(f(-2)=e^{\wedge}(-2) \approx 0.13534\)
Después de aprender a usar tu calculadora particular, ahora puedes bosquejar la gráfica trazando puntos. (Redondear a la centésima más cercana.)
| \(x\) | \(y\) | \(f(x)=e^{x}\) | \(\color{Cerulean}{Solutions} \) |
|---|---|---|---|
| \ (x\) ">\(-2\) | \ (y\) ">\(\color{Cerulean}{0.14}\) | \ (f (x) =e^ {x}\) ">\(f(-2)=e^{-2}=0.14\) | \ (\ color {cerúleo} {Soluciones}\) ">\((-2,0.14)\) |
| \ (x\) ">\(-1\) | \ (y\) ">\(\color{Cerulean}{0.37}\) | \ (f (x) =e^ {x}\) ">\(f(-1)=e^{-1}=0.37\) | \ (\ color {cerúleo} {Soluciones}\) ">\((-1,0.37)\) |
| \ (x\) ">\(0\) | \ (y\) ">\(\color{Cerulean}{1}\) | \ (f (x) =e^ {x}\) ">\(f(0)=e^{0}=1\) | \ (\ color {cerúleo} {Soluciones}\) ">\((0,1)\) |
| \ (x\) ">\(1\) | \ (y\) ">\(\color{Cerulean}{2.72}\) | \ (f (x) =e^ {x}\) ">\(f(1)=e^{1}=2.72\) | \ (\ color {cerúleo} {Soluciones}\) ">\((1,2.72)\) |
| \ (x\) ">\(2\) | \ (y\) ">\(\color{Cerulean}{7.39}\) | \ (f (x) =e^ {x}\) ">\(f(2)=e^{2}=7.39\) | \ (\ color {cerúleo} {Soluciones}\) ">\((2,7.39)\) |
Trazar los puntos y bosquejar la gráfica.
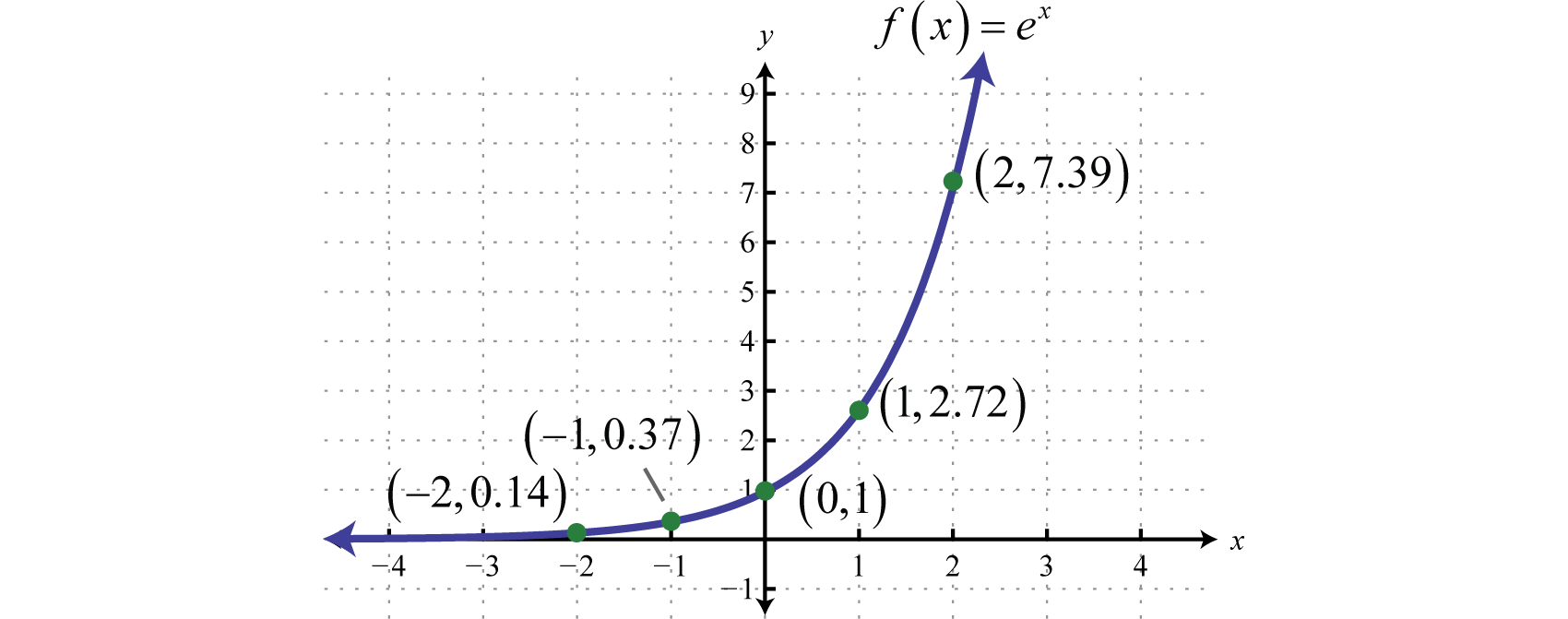
Tenga en cuenta que la función es similar a la gráfica de\(y = 3^{x}\). El dominio consta de todos los números reales y el rango consiste en todos los números reales positivos. Hay una asíntota en\(y = 0\) y una\(y\) -intercepción en\((0, 1)\). Podemos utilizar las transformaciones para esbozar la gráfica de funciones exponenciales más complicadas.
Ejemplo\(\PageIndex{4}\):
Dibuje la gráfica y determine el dominio y el rango:\(g(x)=e^{x+2}-3\).
Solución
Identificar las transformaciones básicas.
\(\begin{array}{l}{y=e^{x}} \quad\quad\quad\:\:\:\color{Cerulean}{Basic\:graph} \\ {y=e^{x+2}} \quad\quad\:\:\:\color{Cerulean}{Shift\:left\:2\:units}\\ {y=e^{x+2}-3}\:\:\:\:\color{Cerulean}{Shift\:down\:3\:units}\end{array}\)
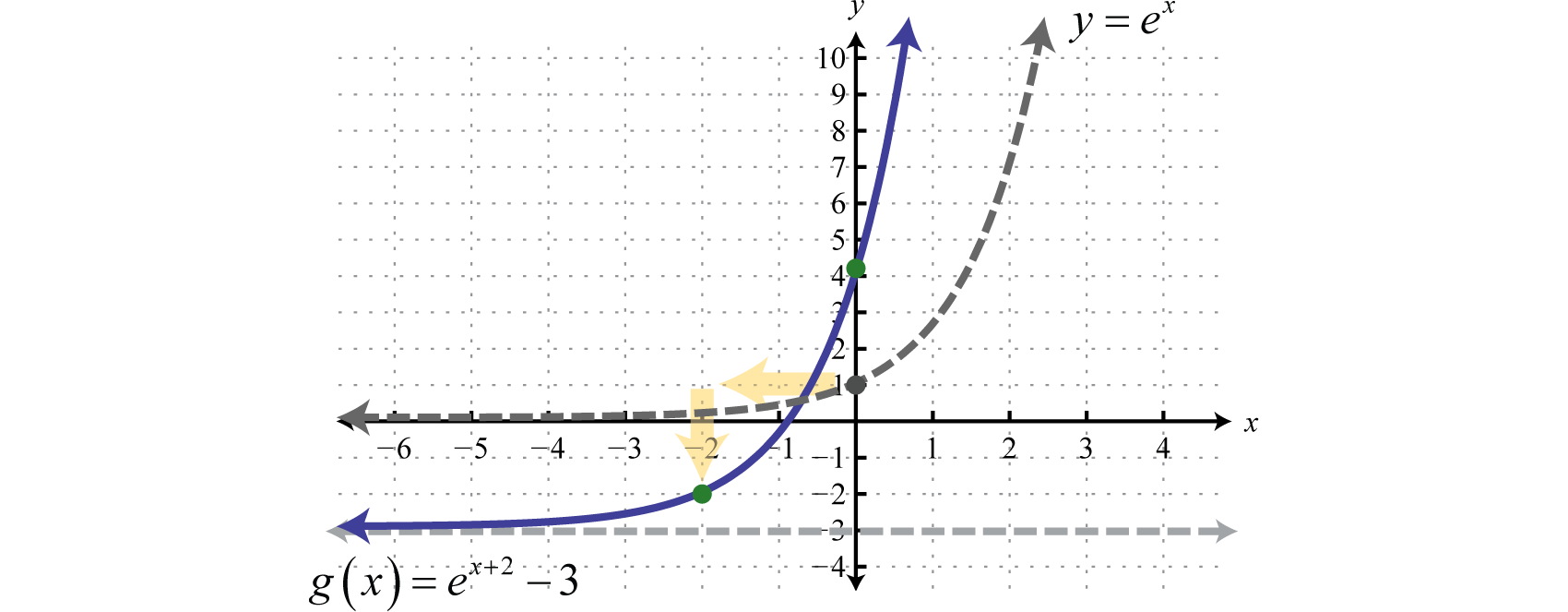
Para determinar el conjunto\(y\) -intercept\(x = 0\).
\(\begin{aligned} g(\color{Cerulean}{0}\color{black}{)} &=e^{\color{Cerulean}{0}\color{black}{+}2}-3 \\ &=e^{2}-3 \\ & \approx 4.39 \end{aligned}\)
Por lo tanto la\(y\) -intercepción es\((0, e^{2} − 3)\).
Contestar
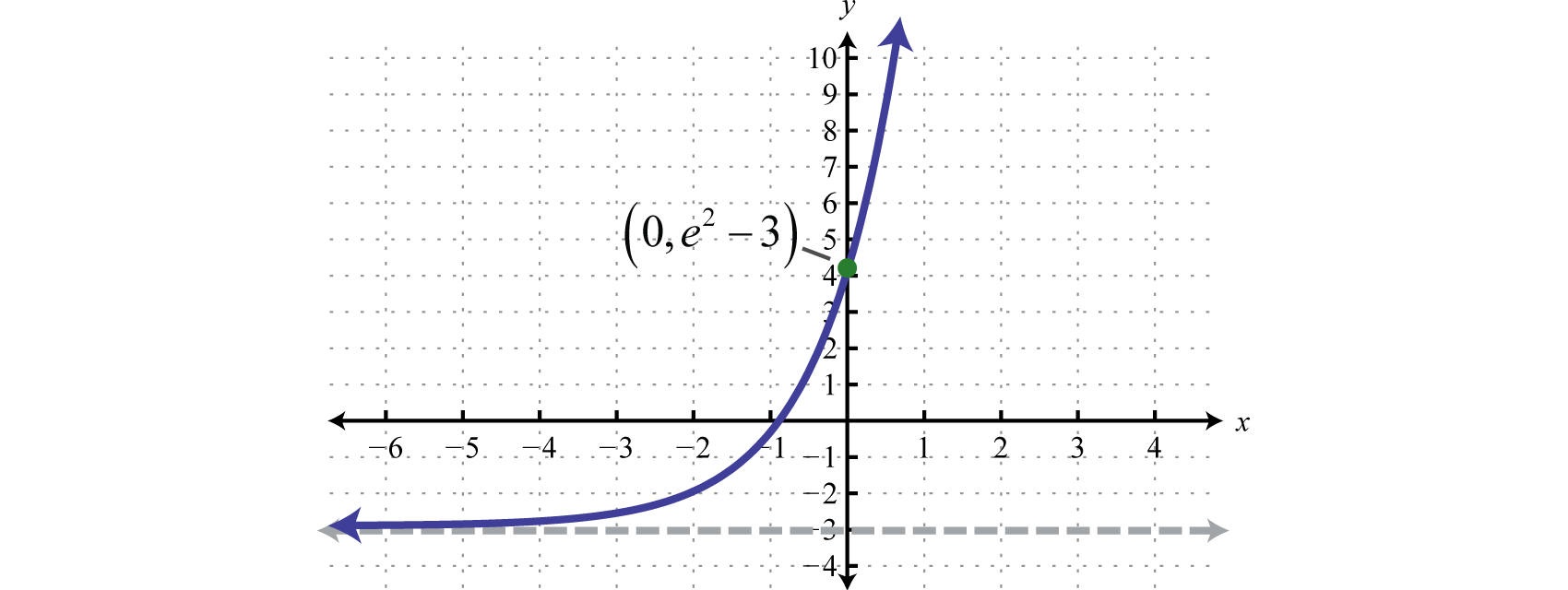
Dominio:\((-\infty, \infty)\); Rango:\((-3, \infty)\)
Ejercicio\(\PageIndex{2}\)
Dibuje la gráfica y determine el dominio y el rango:\(f(x)=e^{-x}+2\).
- Contestar
-
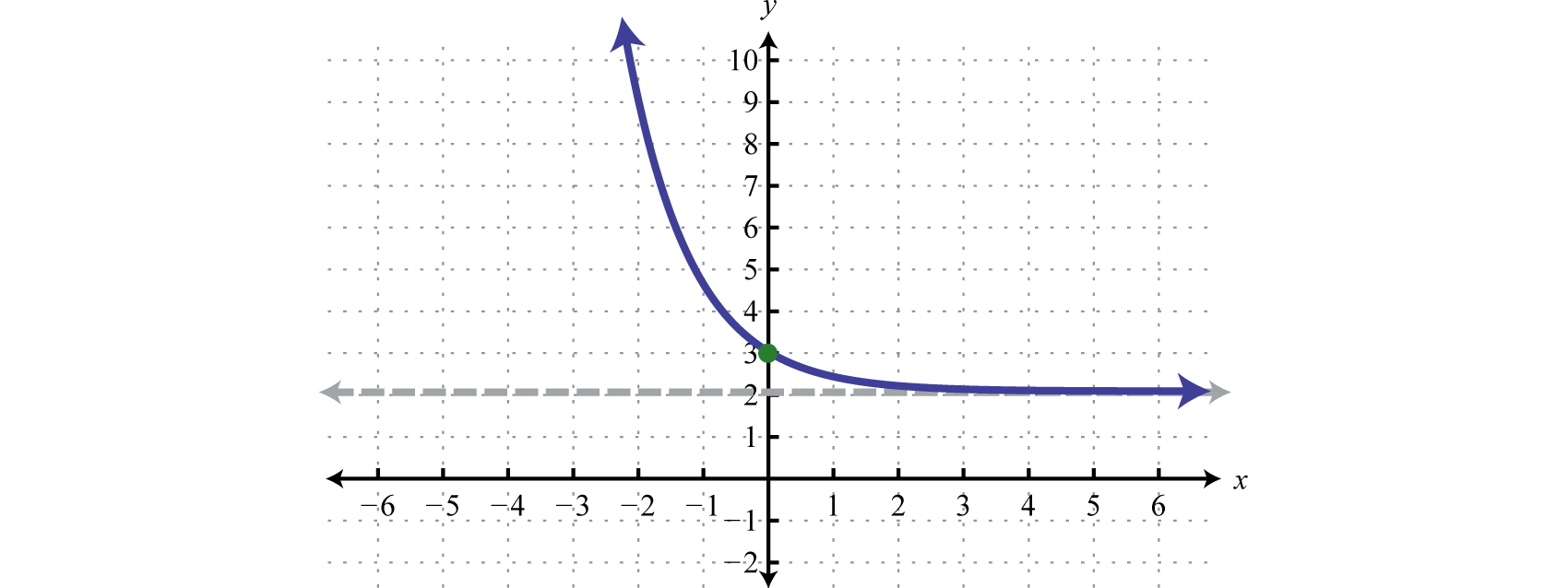
Figura\(\PageIndex{18}\) Dominio:\((-\infty, \infty)\); Rango:\((2, \infty)\)
www.youtube.com/v/fkwbpg2xPB8
Fórmulas de interés compuesto
Las funciones exponenciales aparecen en fórmulas utilizadas para calcular los intereses devengados en la mayoría de las cuentas de ahorro regulares El interés compuesto se produce cuando los intereses acumulados por un período se agregan a la inversión principal antes de calcular los intereses para el siguiente período. La cantidad devengada de esta manera a lo largo del tiempo se modela por la fórmula de interés compuesto 6:
\(A(t)=P\left(1+\frac{r}{n}\right)^{n t}\)
Aquí el monto\(A\) depende del tiempo\(t\) en años en que el principal\(P\) esté acumulando interés compuesto a una tasa de interés anual\(r\). El valor\(n\) representa el número de veces que el interés se compone en un año.
Ejemplo\(\PageIndex{5}\):
Se\(500\) realiza una inversión de $ en un CD\(6\) -año que gana\(4 \frac{1}{2}\)% de interés anual que se compone mensualmente. ¿Cuánto valdrá el CD al final del plazo del\(6\) año?
Solución
Aquí el principal\(P =\) $\(500\), la tasa de interés\(r = 4 \frac{1}{2}\)%\(= 0.045\), y debido a que el interés se compone mensualmente,\(n = 12\). La inversión está modelada por lo siguiente,
\(A(t)=500\left(1+\frac{0.045}{12}\right)^{12 t}\)
Determinar el monto en la cuenta después de\(6\) años evaluar\(A (6)\) y redondear al centavo más cercano.
\(\begin{aligned} A(\color{Cerulean}{6}\color{black}{)} &=500\left(1+\frac{0.045}{12}\right)^{12(\color{Cerulean}{6}\color{black}{)}} \\ &=500(1.00375)^{72} \\ &=654.65 \end{aligned}\)
Contestar
El CD valdrá $\(654.65\) al final del término del\(6\) año.
A continuación exploramos los efectos del aumento\(n\) en la fórmula. En aras de la claridad dejamos\(P\) e\(r\) igualamos\(1\) y calculamos en consecuencia.
| Compuesto anual | \(\left(1+\frac{1}{n}\right)^{n}\) |
|---|---|
| Anual\((n=1)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{1}}\right)}^{\color{Cerulean}{1}}\color{black}{=}2\) |
| Semestral\((n=2)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{2}}\right)}^{\color{Cerulean}{2}}\color{black}{=}2.25\) |
| Trimestral\((n=4)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{4}}\right)}^{\color{Cerulean}{4}}\color{black}{≈}2.44140\) |
| Mensual\((n=12)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{12}}\right)}^{\color{Cerulean}{12}}\color{black}{≈}2.61304\) |
| Semanal\((n=52)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{52}}\right)}^{\color{Cerulean}{52}}\color{black}{≈}2.69260\) |
| Diario\((n=365)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{365}}\right)}^{\color{Cerulean}{365}}\color{black}{≈}2.71457\) |
| Por hora\((n=8760)\) | \ (\ izquierda (1+\ frac {1} {n}\ derecha) ^ {n}\) ">\(\color{black}{\left(1+\frac{1}{\color{Cerulean}{8760}}\right)}^{\color{Cerulean}{8760}}\color{black}{≈}2.71813\) |
Continuando con este patrón, a\(n\) medida que aumenta por decir componiendo cada minuto o incluso cada segundo, podemos ver que el resultado tiende hacia la base natural\(e ≈ 2.71828\). El interés compuesto cada instante conduce a la fórmula de interés compuesto continuamente 7,
\(A(t)=P e^{rt}\)
Aquí\(P\) representa el monto inicial del principal invertido,\(r\) representa la tasa de interés anual y\(t\) representa el tiempo en años en que se permite que la inversión devenga intereses compuestos continuamente.
Ejemplo\(\PageIndex{6}\):
Se\(500\) realiza una inversión de $ en un CD\(6\) -año que gana\(4 \frac{1}{2}\)% de interés anual que se compone continuamente. ¿Cuánto valdrá el CD al final del plazo del\(6\) año?
Solución
Aquí el principal\(P =\) $\(500\), y la tasa de interés\(r = 4 \frac{1}{2}\)%\(= 0.045\). Dado que el interés se agrava continuamente utilizaremos la fórmula\(A (t) = Pe^{rt}\). La inversión está modelada por lo siguiente,
\(A(t)=500 e^{0.045 t}\)
Para determinar el monto en la cuenta después de\(6\) años, evaluar\(A (6)\) y redondear al centavo más cercano.
\(\begin{aligned} A(\color{Cerulean}{6}\color{black}{)} &=500 e^{0.045(\color{Cerulean}{6}\color{black}{)}} \\ &=500 e^{0.27} \\ &=654.98 \end{aligned}\)
Contestar
El CD valdrá $\(654.98\) al final del término del\(6\) año.
Compare los dos ejemplos anteriores y tenga en cuenta que componer continuamente puede no ser tan beneficioso como parece. Si bien es mejor componer el interés con más frecuencia, la diferencia no es tan profunda. Ciertamente, la tasa de interés es un factor mucho mayor en el resultado final.
Ejercicio\(\PageIndex{3}\)
¿Cuánto valdrá un $\(1,200\) CD, ganando\(5.2\)% de interés anual compuesto continuamente, al final de un plazo de\(10\) -año?
- Contestar
-
$\(2,018.43\)
www.youtube.com/V/1aluoJtq5wC
Claves para llevar
- Las funciones exponenciales tienen definiciones de la forma\(f (x) = b^{x}\) donde\(b > 0\) y\(b ≠ 1\). El dominio consta de todos los números reales\((−∞, ∞)\) y el rango consiste en números positivos\((0, ∞)\). Además, todas las funciones exponenciales de esta forma tienen una\(y\) -intercepción\((0, 1)\) y son asintóticas al\(x\) eje.
- Si la base de una función exponencial es mayor que\(1 (b > 1)\), entonces su gráfica aumenta o crece a medida que se lee de izquierda a derecha.
- Si la base de una función exponencial es una fracción propia\((0 < b < 1)\), entonces su gráfica disminuye o decae a medida que se lee de izquierda a derecha.
- El número\(10\) se llama la base común y el número\(e\) se llama la base natural.
- La función exponencial natural definida por\(f (x) = e^{x}\) tiene una gráfica que es muy similar a la gráfica de\(g (x) = 3^{x}\).
- Las funciones exponenciales son uno a uno.
Ejercicio\(\PageIndex{4}\)
Evaluar.
- \(f(x)=3^{x}\)dónde\(f(-2), f(0),\) y\(f(2)\).
- \(f(x)=10^{x}\)dónde\(f(-1), f(0),\) y\(f(1)\).
- \(g(x)=\left(\frac{1}{3}\right)^{x}\)dónde\(g(-1), g(0),\) y\(g(3)\).
- \(g(x)=\left(\frac{3}{4}\right)^{x}\)dónde\(g(-2), g(-1),\) y\(g(0)\).
- \(h(x)=9^{-x}\)dónde\(h(-1), h(0),\) y\(h\left(\frac{1}{2}\right)\).
- \(h(x)=4^{-x}\)dónde\(h(-1), h\left(-\frac{1}{2}\right),\) y\(h(0)\).
- \(f(x)=-2^{x}+1\)dónde\(f(-1), f(0),\) y\(f(3)\).
- \(f(x)=2-3^{x}\)dónde\(f(-1), f(0),\) y\(f(2)\).
- \(g(x)=10^{-x}+20\)dónde\(g(-2), g(-1),\) y\(g(0)\).
- \(g(x)=1-2^{-x}\)dónde\(g(-1), g(0),\) y\(g(1)\).
- Contestar
-
1. \(f(-2)=\frac{1}{9}, f(0)=1, f(2)=9\)
3. \(g(-1)=3, g(0)=1, g(3)=\frac{1}{27}\)
5. \(h(-1)=9, h(0)=1, h\left(\frac{1}{2}\right)=\frac{1}{3}\)
7. \(f(-1)=\frac{1}{2}, f(0)=0, f(3)=-7\)
9. \(g(-2)=120, g(-1)=30, g(0)=21\)
Ejercicio\(\PageIndex{5}\)
Use una calculadora para aproximar lo siguiente a la centésima más cercana.
- \(f(x)=2^{x}+5\)donde\(f(2.5)\).
- \(f(x)=3^{x}-10\)donde\(f(3.2)\).
- \(g(x)=4^{x}\)donde\(g(\sqrt{2})\).
- \(g(x)=5^{x}-1\)donde\(g(\sqrt{3})\).
- \(h(x)=10^{x}\)donde\(h(\pi)\).
- \(h(x)=10^{x} + 1\)donde\(h\left(\frac{\pi}{3}\right)\).
- \(f(x)=10^{-x}-2\)donde\(f(1.5)\).
- \(f(x)=5^{-x}+3\)donde\(f(1.3)\).
- \(f(x)=\left(\frac{2}{3}\right)^{x}+1\)donde\(f(-2.7)\).
- \(f(x)=\left(\frac{3}{5}\right)^{-x}-1\)donde\(f(1.4)\).
- Contestar
-
1. \(10.66\)
3. \(7.10\)
5. \(1385.46\)
7. \(−1.97\)
9. \(3.99\)
Ejercicio\(\PageIndex{6}\)
Esbozar la función y determinar el dominio y el rango. Dibuja la asíntota horizontal con una línea discontinua.
- \(f(x)=4^{x}\)
- \(g(x)=3^{x}\)
- \(f(x)=4^{x}+2\)
- \(f(x)=3^{x}-6\)
- \(f(x)=2^{x-2}\)
- \(f(x)=4^{x+2}\)
- \(f(x)=3^{x+1}-4\)
- \(f(x)=10^{x-4}+2\)
- \(h(x)=2^{x-3}-2\)
- \(h(x)=3^{x+2}+4\)
- \(f(x)=\left(\frac{1}{4}\right)^{x}\)
- \(h(x)=\left(\frac{1}{3}\right)^{x}\)
- \(f(x)=\left(\frac{1}{4}\right)^{x}-2\)
- \(h(x)=\left(\frac{1}{3}\right)^{x}+2\)
- \(g(x)=2^{-x}-3\)
- \(g(x)=3^{-x}+1\)
- \(f(x)=6-10^{-x}\)
- \(g(x)=5-4^{-x}\)
- \(f(x)=5-2^{x}\)
- \(f(x)=3-3^{x}\)
- Contestar
-
1. Dominio:\((-\infty, \infty)\); Rango:\((0, \infty)\)
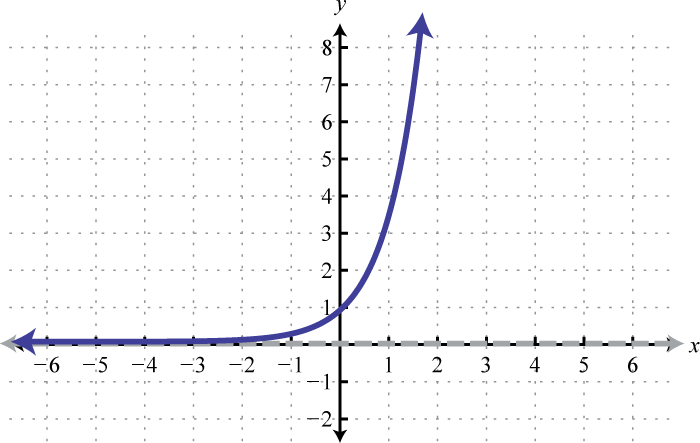
Figura\(\PageIndex{19}\) 3. Dominio:\((-\infty, \infty)\); Rango:\((2, \infty)\)
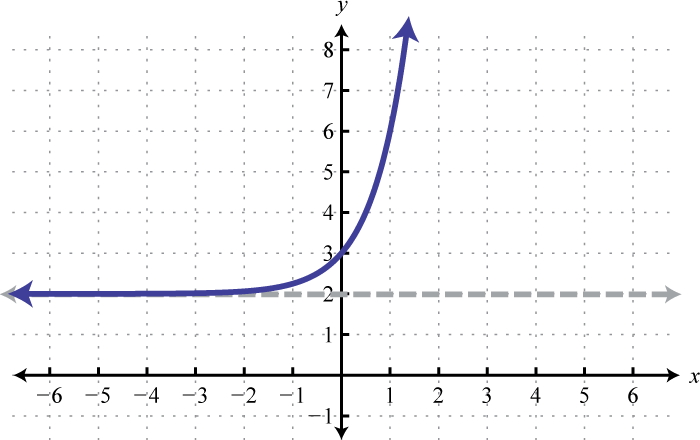
Figura\(\PageIndex{20}\) 5. Dominio:\((-\infty, \infty)\); Rango:\((0, \infty)\)
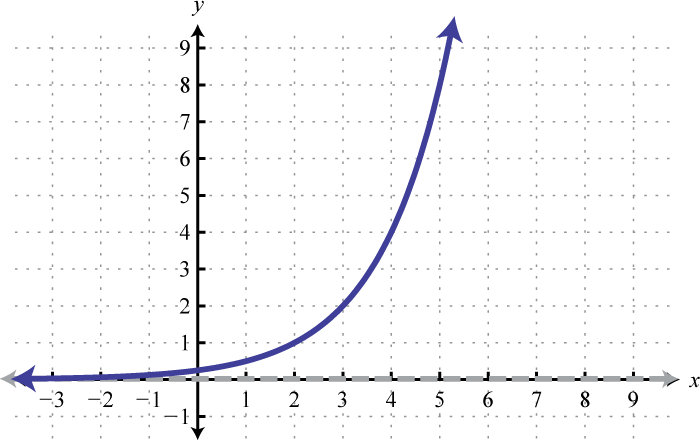
Figura\(\PageIndex{21}\) 7. Dominio:\((-\infty, \infty)\); Rango:\((-4, \infty)\)
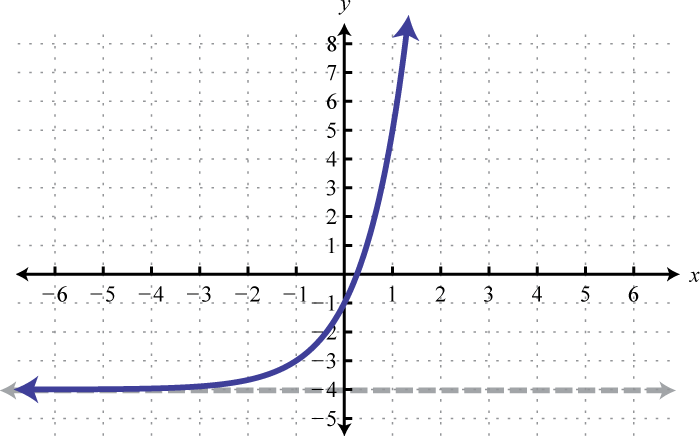
Figura\(\PageIndex{22}\) 9. Dominio:\((-\infty, \infty)\); Rango:\((-2, \infty)\)
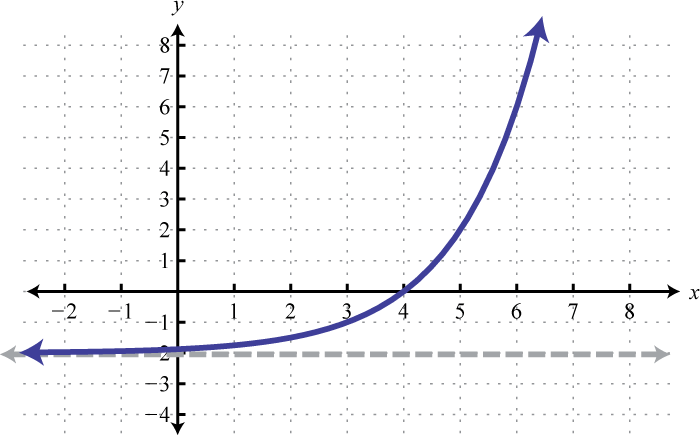
Figura\(\PageIndex{23}\) 11. Dominio:\((-\infty, \infty)\); Rango:\((0, \infty)\)
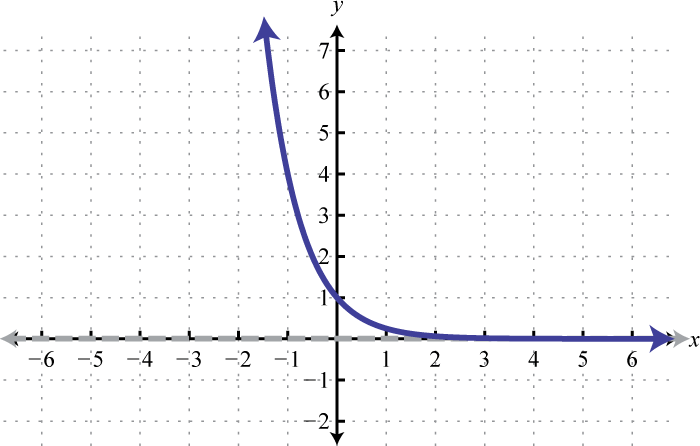
Figura\(\PageIndex{24}\) 13. Dominio:\((-\infty, \infty)\); Rango:\((-2, \infty)\)
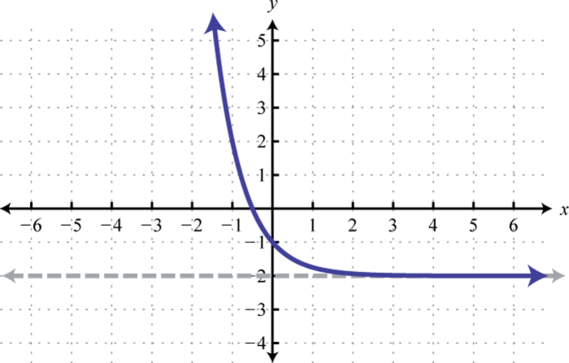
Figura\(\PageIndex{25}\) 15. Dominio:\((-\infty, \infty)\); Rango:\((-3, \infty)\)
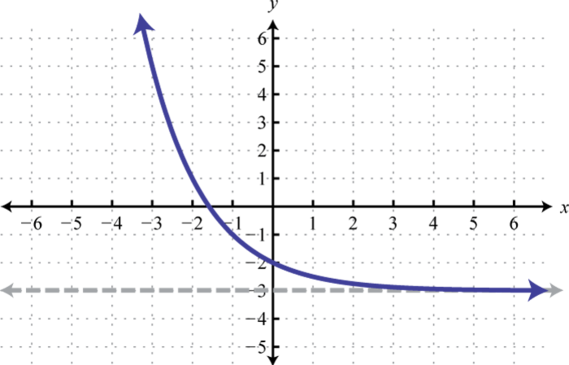
Figura\(\PageIndex{26}\) 17. Dominio:\((-\infty, \infty)\); Rango:\((-\infty, 6)\)

Figura\(\PageIndex{27}\) 19. Dominio:\((-\infty, \infty)\); Rango:\((-\infty, 5)\)
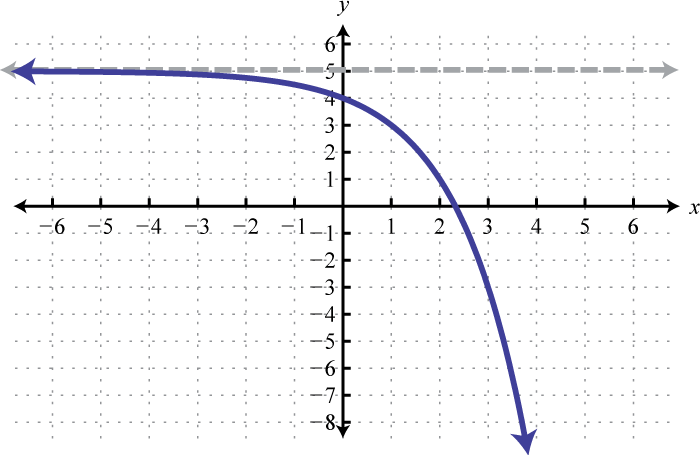
Figura\(\PageIndex{28}\)
Ejercicio\(\PageIndex{7}\)
Buscar\(f (−1), f (0)\), y\(f (\frac{3}{2})\) para la función dada. Use una calculadora en su caso para aproximarse a la centésima más cercana.
- \(f(x)=e^{x}+2\)
- \(f(x)=e^{x}-4\)
- \(f(x)=5-3 e^{x}\)
- \(f(x)=e^{-x}+3\)
- \(f(x)=1+e^{-x}\)
- \(f(x)=3-2 e^{-x}\)
- \(f(x)=e^{-2 x}+2\)
- \(f(x)=e^{-x^{2}}-1\)
- Contestar
-
1. \(f(-1) \approx 2.37, f(0)=3, f\left(\frac{3}{2}\right) \approx 6.48\)
3. \(f(-1) \approx 3.90, f(0)=2, f\left(\frac{3}{2}\right) \approx-8.45\)
5. \(f(-1) \approx 3.72, f(0)=2, f\left(\frac{3}{2}\right) \approx 1.22\)
7. \(f(-1) \approx 9.39, f(0)=3, f\left(\frac{3}{2}\right) \approx 2.05\)
Ejercicio\(\PageIndex{8}\)
Esbozar la función y determinar el dominio y el rango. Dibuja la asíntota horizontal con una línea discontinua.
- \(f(x)=e^{x}-3\)
- \(f(x)=e^{x}+2\)
- \(f(x)=e^{x+1}\)
- \(f(x)=e^{x-3}\)
- \(f(x)=e^{x-2}+1\)
- \(f(x)=e^{x+2}-1\)
- \(g(x)=-e^{x}\)
- \(g(x)=e^{-x}\)
- \(h(x)=-e^{x+1}\)
- \(h(x)=-e^{x}+3\)
- Contestar
-
1. Dominio:\((-\infty, \infty)\); Rango:\((-3, \infty)\)
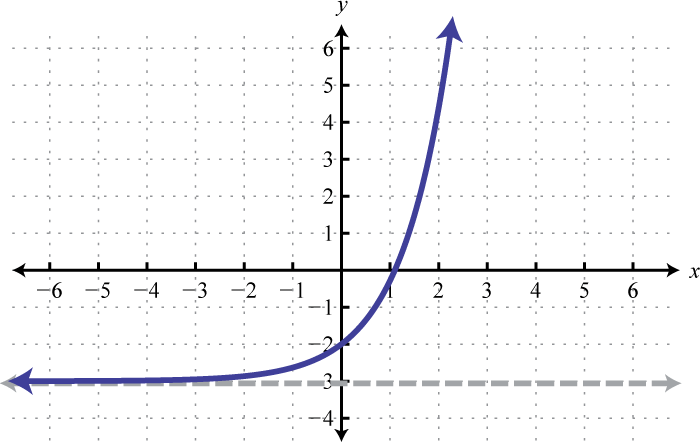
Figura\(\PageIndex{29}\) 3. Dominio:\((-\infty, \infty)\); Rango:\((0, \infty)\)
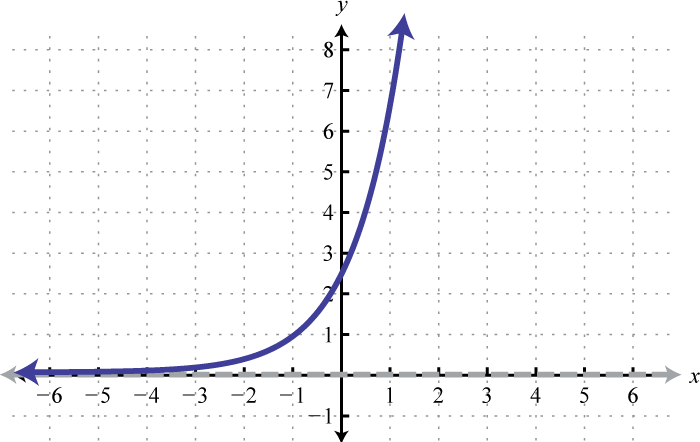
Figura\(\PageIndex{30}\) 5. Dominio:\((-\infty, \infty)\); Rango:\((1, \infty)\)
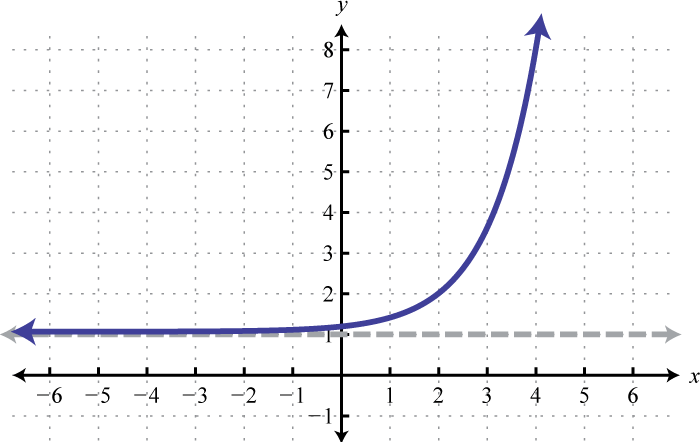
Figura\(\PageIndex{31}\) 7. Dominio:\((-\infty, \infty)\); Rango:\((-\infty, 0)\)
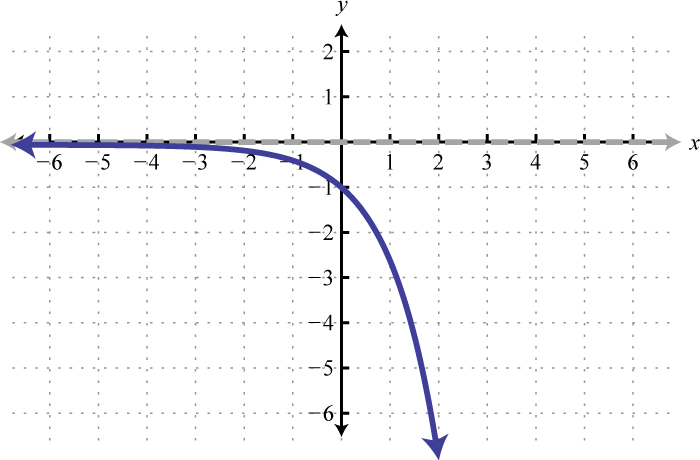
Figura\(\PageIndex{32}\) 9. Dominio:\((-\infty, \infty)\); Rango:\((-\infty, 0)\)
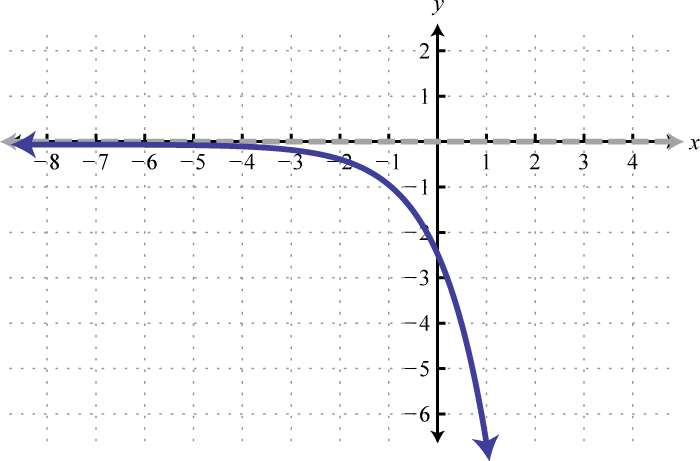
Figura\(\PageIndex{33}\)
Ejercicio\(\PageIndex{9}\)
- Jim invirtió $\(750\) en un CD\(3\) -año que gana\(4.2\)% de interés anual que se compone mensualmente. ¿Cuánto valdrá el CD al final del plazo del\(3\) año?
- José invirtió $\(2,450\) en un CD\(4\) -año que gana\(3.6\)% de interés anual que se compone semestralmente. ¿Cuánto valdrá el CD al final del plazo del\(4\) año?
- Jane tiene sus\(5,350\) ahorros de $ en una cuenta que gana\(3 \frac{5}{8}\)% de interés anual que se compone trimestralmente. ¿Cuánto habrá en la cuenta al final de los\(5\) años?
- Bill tiene $\(12,400\) en una cuenta de ahorro regular ganando\(4 \frac{2}{3}\)% de interés anual que se compone mensualmente. ¿Cuánto habrá en la cuenta al final de los\(3\) años?
- Si $\(85,200\) se invierte en una cuenta que gana\(5.8\)% de interés anual compuesto trimestralmente, entonces ¿cuánto interés se devenga en los primeros\(3\) años?
- Si $\(124,000\) se invierte en una cuenta que gana\(4.6\)% de interés anual compuesto mensualmente, entonces ¿cuánto interés se acumula en los primeros\(2\) años?
- Factura invertida $\(1,400\) en un CD\(3\) -año que gana\(4.2\)% de interés anual que se compone continuamente. ¿Cuánto valdrá el CD al final del plazo del\(3\) año?
- Brooklyn invirtió $\(2,850\) en un CD\(5\) -año que gana\(5.3\)% de interés anual que se agrava continuamente. ¿Cuánto valdrá el CD al final del plazo del\(5\) año?
- Omar tiene sus\(4,200\) ahorros de $ en una cuenta que gana\(4 \frac{3}{8}\)% de interés anual que se agrava continuamente. ¿Cuánto habrá en la cuenta al final de los\(2 \frac{1}{2}\) años?
- Nancy tiene sus\(8,325\) ahorros de $ en una cuenta que gana\(5 \frac{7}{8}\)% de interés anual que se agrava continuamente. ¿Cuánto habrá en la cuenta al final de los\(5 \frac{1}{2}\) años?
- Si $\(12,500\) se invierte en una cuenta que gana\(3.8\)% de interés anual compuesto continuamente, entonces ¿cuánto interés se acumula en los primeros\(10\) años?
- Si $\(220,000\) se invierte en una cuenta que gana\(4.5\)% de interés anual compuesto continuamente, entonces ¿cuánto interés se acumula en los primeros\(2\) años?
- La población de un determinado pueblo pequeño está creciendo de acuerdo a la función\(P (t) = 12,500(1.02)^{t}\) donde\(t\) representa el tiempo en años desde el último censo. Utilizar la función para determinar la población el día del censo (cuándo\(t = 0\)) y estimar la población en\(6\) años a partir de ese momento.
- La población de un determinado pueblo pequeño está disminuyendo de acuerdo a la función\(P (t) = 22,300(0.982)^{t}\) donde\(t\) representa el tiempo en años desde el último censo. Utilizar la función para determinar la población el día del censo (cuándo\(t = 0\)) y estimar la población en\(6\) años a partir de ese momento.
- El valor decreciente, en dólares, de un automóvil nuevo se modela por la fórmula\(V (t) = 28,000(0.84)^{t}\) donde\(t\) representa el número de años después de que se compró el automóvil. Usa la fórmula para determinar el valor del auto cuando era nuevo (\(t = 0\)) y el valor después de\(4\) años.
- El número de visitantes únicos al sitio web de la universidad se puede aproximar por la fórmula\(N (t) = 410(1.32)^{t}\) donde\(t\) representa el número de años después de 1997 cuando se creó el sitio web. Aproximar el número de visitantes únicos al sitio web de la universidad en el año 2020.
- Si no se controla, una nueva cepa del virus de la gripe puede propagarse de una sola persona a otras muy rápidamente. El número de personas afectadas se puede modelar usando la fórmula\(P(t)=e^{0.22 t}\) donde\(t\) representa el número de días que se permite que el virus se propague sin marcar. Estimar el número de personas infectadas con el virus después de\(30\) días y después de\(60\) días.
- Si se deja sin marcar, una población de conejos ingleses\(24\) salvajes puede crecer de acuerdo a la fórmula\(P(t)=24 e^{0.19 t}\) donde el tiempo\(t\) se mide en meses. ¿Cuántos conejos estarían presentes\(3 \frac{1}{2}\) años después?
- La población de cierta ciudad en 1975 era de\(65,000\) personas y crecía exponencialmente a una tasa anual de\(1.7\)%. En su momento, el crecimiento poblacional se modeló por la fórmula\(P (t) = 65,000e^{0.017t}\) donde\(t\) representó el número de años desde 1975. En el año 2000, el censo determinó que la población real era de\(104,250\) personas. ¿Qué población predijo el modelo para el año 2000 y cuál fue el error real?
- Debido a la desintegración radiactiva, la cantidad de una muestra de\(10\) miligramos de yodo-131 disminuye de acuerdo con la fórmula\(A (t) = 10e^{−0.087t}\) donde\(t\) representa el tiempo medido en días. ¿Cuánto de la muestra queda después de\(10\) días?
- El número de células en una muestra de bacterias es aproximado por el modelo de crecimiento logístico\(N(t)=\frac{1.2 \times 10^{5}}{1+9 e^{-0.32 t}}\) donde\(t\) representa el tiempo en horas. Determinar el número inicial de celdas y luego determinar el número de celdas\(6\) horas después.
- La cuota de mercado de un producto, como porcentaje, se aproxima por la fórmula\(P(t)=\frac{100}{2+e^{-0.44 t}}\) donde\(t\) representa el número de meses después de que se lanza una campaña publicitaria agresiva. ¿En cuánto podemos esperar que aumente la cuota de mercado después de los tres primeros meses de publicidad?
- Contestar
-
1. $\(850.52\)
3. $\(6,407.89\)
5. $\(16,066.13\)
7. $\(1,588.00\)
9. $\(4,685.44\)
11. $\(5,778.56\)
13. Población inicial:\(12,500\); Población\(6\) años después:\(14,077\)
15. Nuevo: $\(28,000\); En\(4\) años: $\(13,940.40\)
17. \(30\)Días pasados:\(735\) personas;\(60\) Días pasados:\(540,365\) personas
19. Modelo:\(99,423\) people; error:\(4,827\) people
21. Inicialmente hay\(12,000\) celdas y\(6\) horas después hay\(51,736\) celdas.
Ejercicio\(\PageIndex{10}\)
- ¿Por qué se\(b = 1\) excluye como base en la definición de funciones exponenciales? Explique.
- Explique por qué una función exponencial de la forma nunca\(y = b^{x}\) puede ser negativa.
- Investigar y discutir la derivación de la fórmula de interés compuesto.
- Investigar y discutir el modelo de crecimiento logístico. Proporcione un enlace para obtener más información sobre este tema.
- Investigar y discutir la vida y aportes de Leonhard Euler.
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar
5. La respuesta puede variar
Notas al pie
5 Cualquier función con una definición de la forma\(f (x) = b^{x}\) donde\(b > 0\) y\(b ≠ 1\).
6 Una fórmula que da la cantidad acumulada por la obtención de intereses sobre el principal y los intereses a lo largo del tiempo:\(A(t)=P\left(1+\frac{r}{n}\right)^{n t}\).
7 Una fórmula que da la, cantidad acumulada al ganar intereses continuamente compuestos:\(A (t) = Pe^{rt}\).


