7.E: Funciones Exponenciales y Logarítmicas (Ejercicios)
- Page ID
- 109855
Ejercicio\(\PageIndex{1}\)
Dado\(f\) y\(g\) encontrar\((f \circ g)(x)\) y\((g \circ f)(x)\).
- \(f(x)=6 x-5, g(x)=2 x+1\)
- \(f(x)=5-6 x, g(x)=\frac{3}{2} x\)
- \(f(x)=2 x^{2}+x-2, g(x)=5 x\)
- \(f(x)=x^{2}-x-6, g(x)=x-3\)
- \(f(x)=\sqrt{x+2}, g(x)=8 x-2\)
- \(f(x)=\frac{x-1}{3 x-1}, g(x)=\frac{1}{x}\)
- \(f(x)=x^{2}+3 x-1, g(x)=\frac{1}{x-2}\)
- \(f(x)=\sqrt[3]{3(x+2)}, g(x)=9 x^{3}-2\)
- Contestar
-
1. \((f \circ g)(x)=12 x+1 ;(g \circ f)(x)=12 x-9\)
3. \(\begin{array}{l}{(f \circ g)(x)=50 x^{2}+5 x-2}; \: {(g \circ f)(x)=10 x^{2}+5 x-10}\end{array}\)
5. \((f\circ g)(x)=2\sqrt{2x};\:(g\circ f)(x)=8\sqrt{x+2}-2\)
7. \(\begin{array}{c}{(f \circ g)(x)=-\frac{x^{2}-7 x+9}{(x-2)^{2}}}; \: {\left(g \circ f\right)(x)=\frac{1}{x^{2}+3 x-3}}\end{array}\)
Ejercicio\(\PageIndex{1}\)
¿Las funciones dadas son una a una? Explique.
1.
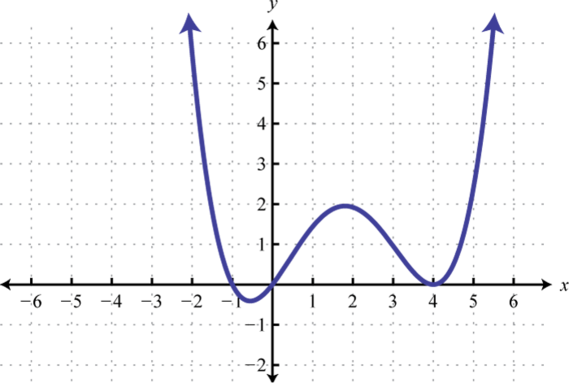
Figura 7.E.1
2.
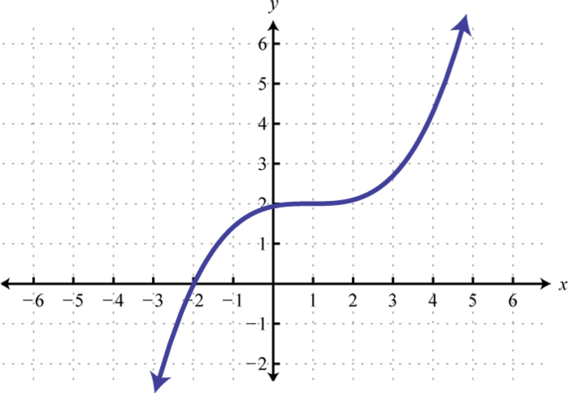
Figura 7.E.2
3.
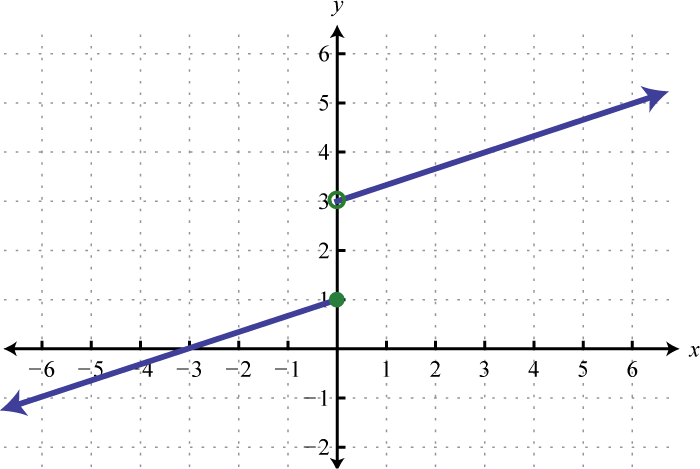
Figura 7.E.3
4.
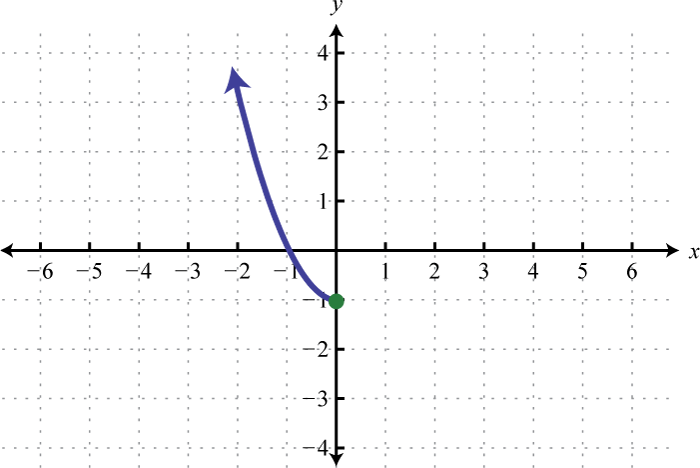
Figura 7.E.4
- Contestar
-
1. No, falla el HLT
3. Sí, pasa el HLT
Ejercicio\(\PageIndex{3}\)
Verificar algebraicamente que las dos funciones dadas son inversas. En otras palabras,\(\left(f \circ f^{-1}\right)(x)=x\) demuéstralo y\(\left(f^{-1} \circ f\right)(x)=x\).
- \(f(x)=6 x-5, f^{-1}(x)=\frac{1}{6} x+\frac{5}{6}\)
- \(f(x)=\sqrt{2 x+3}, f^{-1}(x)=\frac{x^{2}-3}{2}, x \geq 0\)
- \(f(x)=\frac{x}{3 x-2}, f^{-1}(x)=\frac{2 x}{3 x-1}\)
- \(f(x)=\sqrt[3]{x+3}-4, f^{-1}(x)=(x+4)^{3}-3\)
- Contestar
-
1. Prueba
3. Prueba
Ejercicio\(\PageIndex{4}\)
Encuentra las inversas de cada función definida de la siguiente manera:
- \(f(x)=-7 x+3\)
- \(f(x)=\frac{2}{3} x-\frac{1}{2}\)
- \(g(x)=x^{2}-12, x \geq 0\)
- \(g(x)=(x-1)^{3}+5\)
- \(g(x)=\frac{2}{x-1}\)
- \(h(x)=\frac{x+5}{x-5}\)
- \(h(x)=\frac{3 x-1}{x}\)
- \(p(x)=\sqrt[3]{5 x}+3\)
- \(h(x)=\sqrt[3]{2 x-7}+2\)
- \(h(x)=\sqrt[5]{x+2}-3\)
- Contestar
-
1. \(f^{-1}(x)=-\frac{1}{7} x+\frac{3}{7}\)
3. \(g^{-1}(x)=\sqrt{x+12}\)
5. \(g^{-1}(x)=\frac{x+2}{x}\)
7. \(h^{-1}(x)=-\frac{1}{x-3}\)
9. \(h^{-1}(x)=\frac{(x-2)^{3}+7}{2}\)
Ejercicio\(\PageIndex{5}\)
Evaluar.
- \(f(x)=5^{x} ;\)encontrar\(f(-1), f(0),\) y\(f(3).\)
- \(f(x)=\left(\frac{1}{2}\right)^{x} ;\)encontrar\(f(-4), f(0),\) y\(f(-3).\)
- \(g(x)=10^{-x} ;\)encontrar\(g(-5), g(0),\) y\(g(2).\)
- \(g(x)=1-3^{x} ;\)encontrar\(g(-2), g(0),\) y\(g(3).\)
- Contestar
-
1. \(f(-1)=\frac{1}{5}, f(0)=1, f(3)=125\)
3. \(g(-5)=100,000, g(0)=1, g(2)=\frac{1}{100}\)
Ejercicio\(\PageIndex{6}\)
Esbozar la función exponencial. Dibuja la asíntota horizontal con una línea discontinua.
- \(f(x)=5^{x}+10\)
- \(f(x)=5^{x-4}\)
- \(f(x)=-3^{x}-9\)
- \(f(x)=3^{x+2}+6\)
- \(f(x)=\left(\frac{1}{3}\right)^{x}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}-4\)
- \(f(x)=2^{-x}+3\)
- \(f(x)=1-3^{-x}\)
- Contestar
-
1.
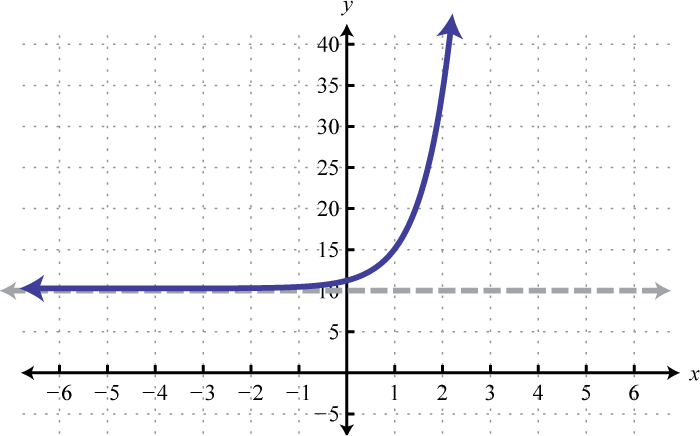
Figura 7.E.5
3.
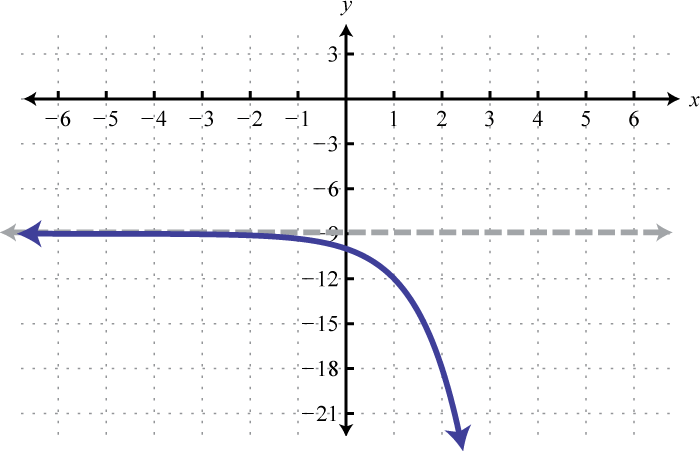
Figura 7.E.6
5.
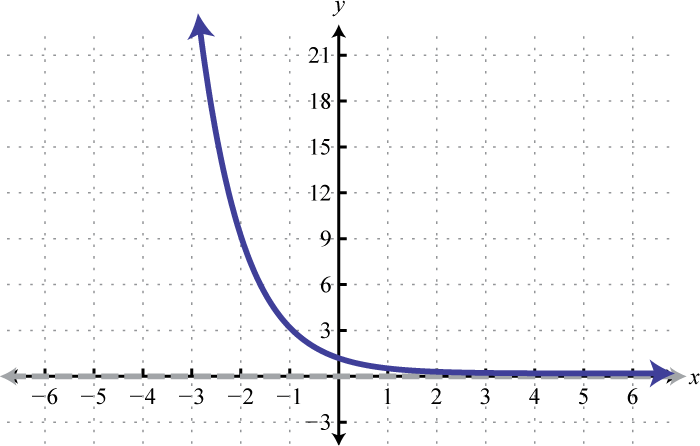
Figura 7.E.7
7.
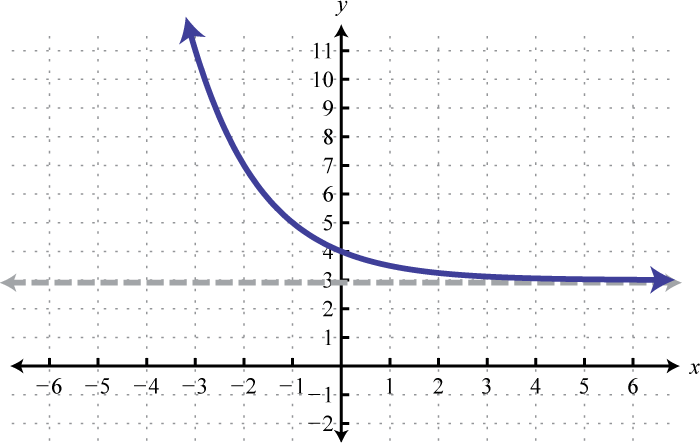
Figura 7.E.8
Ejercicio\(\PageIndex{7}\)
Utilice una calculadora para evaluar lo siguiente. Redondear a la centésima más cercana.
- \(f(x)=e^{x}+1 ;\)encontrar\(f(-3), f(-1),\) y\(f\left(\frac{1}{2}\right)\).
- \(g(x)=2-3 e^{x} ;\)encontrar\(g(-1), g(0),\) y\(g\left(\frac{2}{3}\right)\).
- \(p(x)=1-5 e^{-x} ;\)encontrar\(p(-4), p\left(-\frac{1}{2}\right),\) y\(p(0)\).
- \(r(x)=e^{-2 x}-1 ;\)encontrar\(r(-1), r\left(\frac{1}{4}\right),\) y\(r(2)\).
- Contestar
-
1. \(f(-3) \approx 1.05, f(-1) \approx 1.37, f\left(\frac{1}{2}\right) \approx 2.65\)
3. \(p(-4) \approx-271.99, p\left(-\frac{1}{2}\right) \approx-7.24, p(0)=-4\)
Ejercicio\(\PageIndex{8}\)
Croquis de la función. Dibuja la asíntota horizontal con una línea discontinua.
- \(f(x)=e^{x}+4\)
- \(f(x)=e^{x-4}\)
- \(f(x)=e^{x+3}+2\)
- \(f(x)=e^{-x}+5\)
- Jerry invirtió $\(6,250\) en una cuenta ganando\(3 \frac{5}{8}\)% de interés anual que se compone mensualmente. ¿Cuánto habrá en la cuenta después de\(4\) años?
- José invirtió $\(7,500\) en una cuenta ganando\(4 \frac{1}{4}\)% de interés anual que se agrava continuamente. ¿Cuánto habrá en la cuenta después de\(3 \frac{1}{2}\) años?
- Una muestra de\(14\) -gramo de yodo radiactivo se libera accidentalmente a la atmósfera. La cantidad de la sustancia en gramos viene dada por la fórmula\(P (t) = 14e^{ −0.087t}\), donde\(t\) representa el tiempo en días posteriores a la liberación de la muestra. ¿Cuánto yodo radiactivo estará presente en la atmósfera\(30\) días después de su liberación?
- El número de células en una muestra de bacterias viene dado por la fórmula\(N(t)=\frac{2.4 \times 10^{5}}{1+9 e^{-0.28t}}\), donde\(t\) representa el tiempo en horas desde la colocación inicial de\(24,000\) las células. Usa la fórmula para calcular el número de celdas en la muestra\(20\) horas después.
- Contestar
-
1.
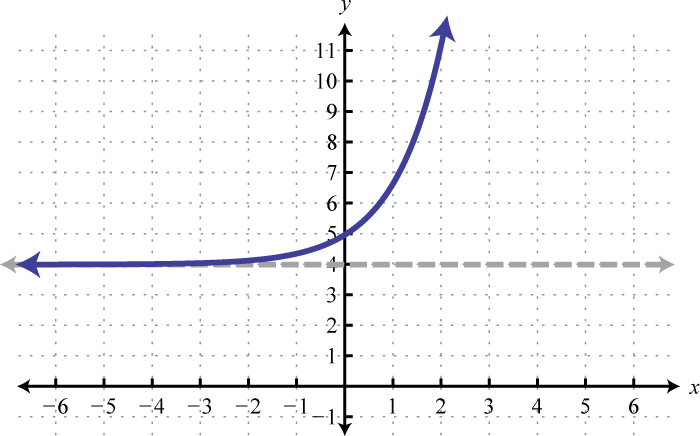
Figura 7.E.9
3.
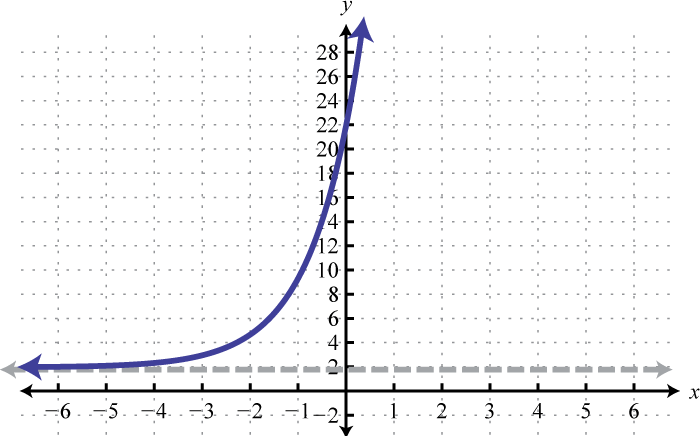
Figura 7.E.10
5. $\(7,223.67\)
7. Aproximadamente\(1\) gram
Ejercicio\(\PageIndex{9}\)
Evaluar.
- \(\log _{4} 16\)
- \(\log _{3} 27\)
- \(\log _{2}\left(\frac{1}{32}\right)\)
- \(\log \left(\frac{1}{10}\right)\)
- \(\log _{1 / 3} 9\)
- \(\log _{3 / 4}\left(\frac{4}{3}\right)\)
- \(\log _{7} 1\)
- \(\log _{3}(-3)\)
- \(\log _{4} 0\)
- \(\log _{3} 81\)
- \(\log _{6} \sqrt{6}\)
- \(\log _{5} \sqrt[3]{25}\)
- \(\ln e^{8}\)
- \(\ln \left(\frac{1}{e^{5}}\right)\)
- \(\log (0.00001)\)
- \(\log 1,000,000\)
- Contestar
-
1. \(2\)
3. \(−5\)
5. \(−2\)
7. \(0\)
9. Sin definir
11. \(\frac{1}{2}\)
13. \(8\)
15. \(−5\)
Ejercicio\(\PageIndex{10}\)
Encuentra\(x\).
- \(\log _{5} x=3\)
- \(\log _{3} x=-4\)
- \(\log _{2 / 3} x=3\)
- \(\log _{3} x=\frac{2}{5}\)
- \(\log x=-3\)
- \(\ln x=\frac{1}{2}\)
- Contestar
-
1. \(125\)
3. \(\frac{8}{27}\)
5. \(0.001\)
Ejercicio\(\PageIndex{11}\)
Dibuje la gráfica de la función logarítmica. Dibuja la asíntota vertical con una línea discontinua.
- \(f(x)=\log _{2}(x-5)\)
- \(f(x)=\log _{2} x-5\)
- \(g(x)=\log _{3}(x+5)+15\)
- \(g(x)=\log _{3}(x-5)-5\)
- \(h(x)=\log _{4}(-x)+1\)
- \(h(x)=3-\log _{4} x\)
- \(g(x)=\ln (x-2)+3\)
- \(g(x)=\ln (x+3)-1\)
- La población de cierto pueblo pequeño está creciendo de acuerdo a la función\(P (t) = 89,000(1.035)^{t}\), donde\(t\) representa el tiempo en años desde el último censo. Utilizar la función para estimar la población\(8 \frac{1}{2}\) años después de que se realizó el censo.
- El volumen de sonido\(L\) en decibelios (dB) viene dado por la fórmula\(L=10 \log \left(I / 10^{-12}\right)\), donde\(I\) representa la intensidad del sonido en vatios por metro cuadrado. Determinar el volumen de un sonido con una intensidad de\(0.5\) vatios por metro cuadrado.
- Contestar
-
1.
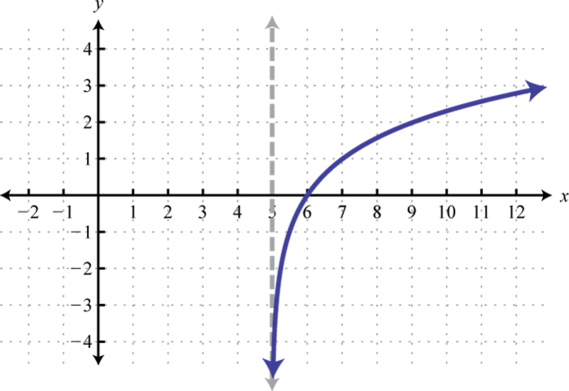
Figura 7.E.11
3.
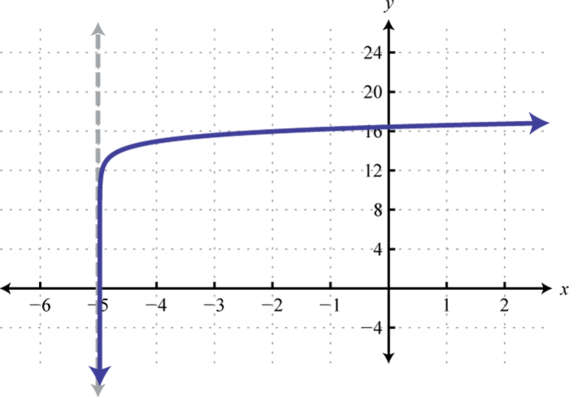
Figura 7.E.12
5.
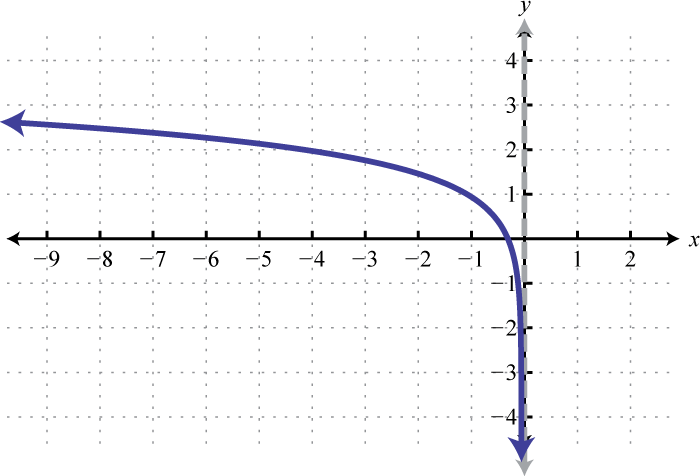
Figura 7.E.13
7.
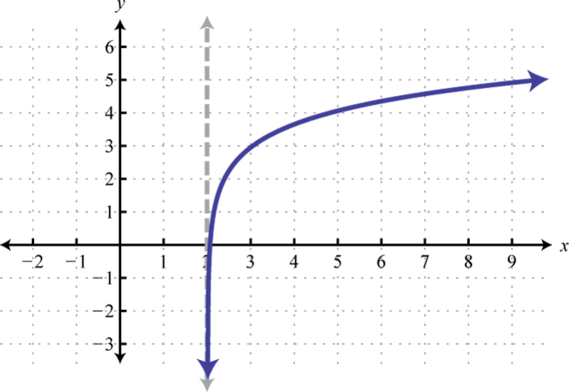
Figura 7.E.14
9. \(119,229\)personas
Ejercicio\(\PageIndex{12}\)
Evaluar sin usar una calculadora.
- \(\log _{9} 9\)
- \(\log _{8} 1\)
- \(\log _{1 / 3} 3\)
- \(\log \left(\frac{1}{10}\right)\)
- \(e^{\ln 17}\)
- \(10^{\log 27}\)
- \(\ln e^{63}\)
- \(\log 10^{33}\)
- Contestar
-
1. \(1\)
3. \(−1\)
5. \(17\)
7. \(63\)
Ejercicio\(\PageIndex{13}\)
Ampliar completamente.
- \(\log \left(100 x^{2}\right)\)
- \(\log _{5}\left(5 x^{3}\right)\)
- \(\log _{3}\left(\frac{3 x^{5}}{5}\right)\)
- \(\ln \left(\frac{10}{3 x^{2}}\right)\)
- \(\log _{2}\left(\frac{8 x^{2}}{y^{2} z}\right)\)
- \(\log \left(\frac{x^{10}}{10 y^{3} z^{4}}\right)\)
- \(\ln \left(\frac{3 b \sqrt{a}}{c^{4}}\right)\)
- \(\log \left(\frac{20 y^{3}}{\sqrt[3]{x^{2}}}\right)\)
- Contestar
-
1. \(2+2 \log x\)
3. \(1+5 \log _{3} x-\log _{3} 5\)
5. \(3+2 \log _{2} x-2 \log _{2} y-\log _{2} z\)
7. \(\ln 3+\ln b+\frac{1}{2} \ln a-4 \ln c\)
Ejercicio\(\PageIndex{14}\)
Escribir como un logaritmo único con coeficiente\(1\).
- \(\log x+2 \log y-3 \log z\)
- \(\log _{2} 5-3 \log _{2} x+4 \log _{2} y\)
- \(-2 \log _{5} x+\log _{5} y-5 \log _{5}(x-1)\)
- \(\ln x-\ln (x-1)-\ln (x+1)\)
- \(3 \log _{2} x+\frac{1}{2} \log _{2} y-\frac{2}{3} \log _{2} z\)
- \(\frac{1}{3} \log x-3 \log y-\frac{3}{5} \log z\)
- \(\log _{5} 4+5 \log _{5} x-\frac{1}{3}\left(\log _{5} y+2 \log _{5} z\right)\)
- \(\ln x-\frac{1}{2}(\ln y-4 \ln z)\)
- Contestar
-
1. \(\log \left(\frac{x y^{2}}{z^{3}}\right)\)
3. \(\log _{5}\left(\frac{y}{x^{2}(x-1)^{5}}\right)\)
5. \(\log _{2}\left(\frac{x^{3} \sqrt{y}}{\sqrt[3]{z^{2}}}\right)\)
7. \(\log _{5}\left(\frac{4 x^{5}}{\sqrt[3]{y z^{2}}}\right)\)
Ejercicio\(\PageIndex{15}\)
Resolver. Dar la respuesta exacta y la respuesta aproximada redondeada a la centésima más cercana en su caso.
- \(5^{2 x+1}=125\)
- \(10^{3 x-2}=100\)
- \(9^{x-3}=81\)
- \(16^{2 x+3}=8\)
- \(5^{x}=7\)
- \(3^{2 x}=5\)
- \(10^{x+2}-3=7\)
- \(e^{2 x-1}+2=3\)
- \(7^{4 x-1}-2=9\)
- \(3^{5 x-2}+5=7\)
- \(3-e^{4 x}=2\)
- \(5+e^{3 x}=4\)
- \(\frac{4}{1+e^{5 x}}=2\)
- \(\frac{100}{1+e^{3 x}}=\frac{1}{2}\)
- Contestar
-
1. \(1\)
3. \(5\)
5. \(\frac{\log (7)}{\log (5)} \approx 1.21\)
7. \(-1\)
9. \(\frac{\log 7+\log 11}{4 \log 7} \approx 0.56\)
11. \(0\)
13. \(0\)
Ejercicio\(\PageIndex{16}\)
Utilice el cambio de fórmula base para aproximar lo siguiente a la décima más cercana.
- \(\log _{5} 13\)
- \(\log _{2} 27\)
- \(\log _{4} 5\)
- \(\log _{9} 0.81\)
- \(\log _{1 / 4} 21\)
- \(\log _{2} \sqrt[3]{5}\)
- Contestar
-
1. \(1.6\)
3. \(1.2\)
5. \(-2.2\)
Ejercicio\(\PageIndex{17}\)
Resolver.
- \(\log _{2}(3 x-5)=\log _{2}(2 x+7)\)
- \(\ln (7 x)=\ln (x+8)\)
- \(\log _{5} 8-2 \log _{5} x=\log _{5} 2\)
- \(\log _{3}(x+2)+\log _{3}(x)=\log _{3} 8\)
- \(\log _{5}(2 x-1)=2\)
- \(2 \log _{4}(3 x-2)=4\)
- \(2=\log _{2}\left(x^{2}-4\right)-\log _{2} 3\)
- \(\log _{2}(x-1)+\log _{2}(x+1)=3\)
- \(\log _{2} x+\log _{2}(x-1)=1\)
- \(\log _{4}(x+5)+\log _{4}(x+11)=2\)
- \(\log (2 x+5)-\log (x-1)=1\)
- \(\ln x-\ln (2 x-1)=1\)
- \(2 \log _{2}(x+4)=\log _{2}(x+2)+3\)
- \(2 \log _{3} x=1+\log _{3}(x+6)\)
- \(\log _{3}(x+1)-2 \log _{3} x=1\)
- \(\log _{5}(2 x)+\log _{5}(x-1)=1\)
- Contestar
-
1. \(12\)
3. \(2\)
5. \(13\)
7. \(±4\)
9. \(2\)
11. \(\frac{15}{8}\)
13. \(0\)
15. \(\frac{1+\sqrt{13}}{6}\)
Ejercicio\(\PageIndex{18}\)
Resolver.
- \(3,250\)Se invierte una cantidad de $ en una cuenta que gana\(4.6\)% de interés anual que se compone mensualmente. Estimar el número de años para que el monto en la cuenta alcance $\(4,000\).
- \(2,500\)Se invierte una cantidad de $ en una cuenta que gana\(5.5\)% de interés anual que se compone continuamente. Estimar el número de años para que el monto en la cuenta alcance $\(3,000\).
- ¿Cuánto tiempo se tarda en duplicar una inversión realizada en una cuenta que gana\(6 \frac{3}{4}\)% de interés anual que se compone continuamente?
- ¿Cuánto tiempo se tarda en duplicar una inversión realizada en una cuenta que gana\(6 \frac{3}{4}\)% de interés anual que se compone semestralmente?
- En el año 2000 un cierto pueblo pequeño tenía una población de\(46,000\) personas. En el año 2010 se estimó que la población había crecido a\(92,000\) personas. Si la población continúa creciendo exponencialmente a este ritmo, estime la población en el año 2016.
- Se compró una camioneta de flota nueva por $\(28,000\) y\(2\) años después se valoró en $\(20,000\). Si el valor de la camioneta sigue disminuyendo exponencialmente a esta tasa, determine su valor\(7\) años después de que sea comprada nueva.
- Un sitio web que ha estado en declive registró visitantes\(4,200\) únicos el mes pasado y visitantes\(3,600\) únicos este mes. Si el número de visitantes únicos sigue disminuyendo exponencialmente, ¿cuántos visitantes únicos esperarías el próximo mes?
- Se introdujo una población inicial de\(18\) conejos en una reserva de vida silvestre. El número de conejos se duplicó en el primer año. Si la población de conejos sigue creciendo exponencialmente a este ritmo, ¿cuántos conejos estarán presentes\(5\) años después de su introducción?
- La vida media del sodio-24 es de aproximadamente\(15\) horas. ¿Cuánto tiempo tardará una muestra de\(50\) -miligramo en decairse a\(10\) miligramos?
- La vida media del radio-226 es de aproximadamente\(1,600\) años. ¿Cuánto tiempo tardará una muestra inicial en decairse al\(30\)% de la cantidad original?
- Un arqueólogo descubrió un artefacto de herramienta ósea. Después del análisis, se encontró que el artefacto contenía\(62\)% del carbono-14 que normalmente se encuentra en el hueso del mismo animal. Dado que el carbono-14 tiene una vida media de\(5,730 years\), estimar la edad del artefacto.
- La vida media del yodo-131 radiactivo es de aproximadamente\(8\) días. ¿Qué porcentaje de una muestra inicial liberada accidentalmente a la atmósfera esperamos que quede después de\(53\) días?
- Contestar
-
1. \(4.5\)años
3. \(10.27\)años
5. Acerca de\(139,446\) las personas
7. \(3,086\)visitantes únicos
9. \(35\)horas
11. Acerca de\(3,952\) años
Examen de muestra
Ejercicio\(\PageIndex{19}\)
- Dado\(f(x)=x^{2}-x+3\) y\(g(x)=3 x-1\) encontrar\((f \circ g)(x)\).
- \(g(x)=\frac{x^{3}+2}{7}\)Demuéstralo\(f(x)=\sqrt[3]{7 x-2} \) y son inversos.
- Contestar
-
1. \((f \circ g)(x)=9 x^{2}-9 x+5\)
Ejercicio\(\PageIndex{20}\)
Encuentra la inversa de las siguientes funciones:
- \(f(x)=\frac{1}{2} x-3\)
- \(h(x)=x^{2}+3\)donde\(x \geq 0\)
- Contestar
-
1. \(f^{-1}(x)=2 x+6\)
Ejercicio\(\PageIndex{21}\)
Esbozar la gráfica.
- \(f(x)=e^{x}-5\)
- \(g(x)=10^{-x}\)
- Joe invirtió $\(5,200\) en una cuenta ganando\(3.8\)% de interés anual que se compone mensualmente. ¿Cuánto habrá en la cuenta al final de los\(4\) años?
- Mary tiene $\(3,500\) en una cuenta de ahorro ganando\(4 \frac{1}{2}\)% de interés anual que se agrava continuamente. ¿Cuánto habrá en la cuenta al final de los\(3\) años?
- Contestar
-
1.
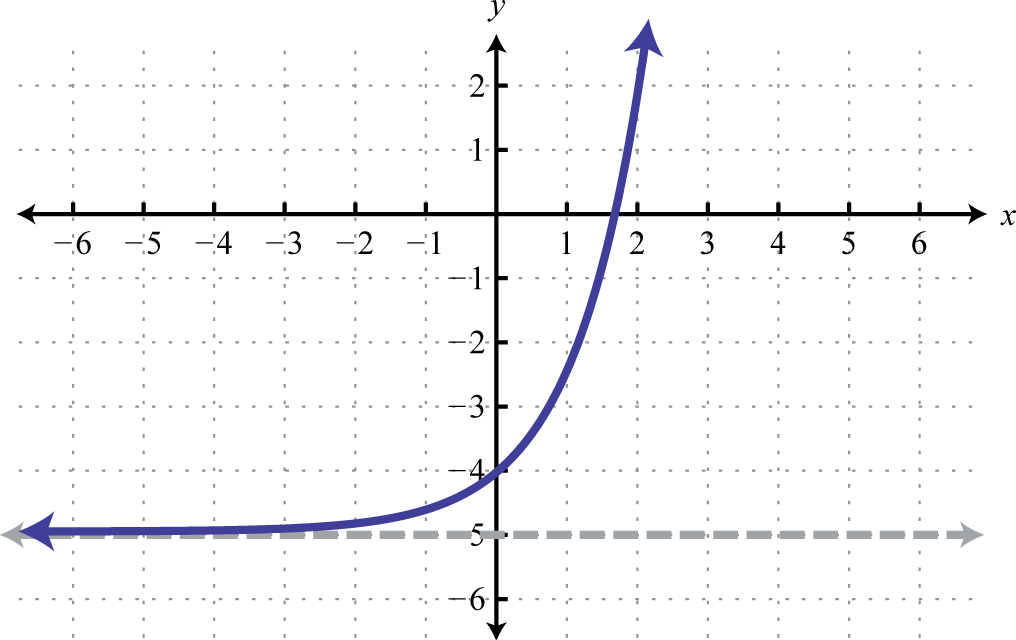
Figura 7.E.15
3. $\(6,052.18\)
Ejercicio\(\PageIndex{22}\)
Evaluar.
- \(\log _{3} 81\)
- \(\log _{2}\left(\frac{1}{4}\right)\)
- \(\log 1,000\)
- \(\ln e\)
- \(\log _{4} 2\)
- \(\log _{9}\left(\frac{1}{3}\right)\)
- \(\ln e^{3}\)
- \(\log _{1 / 5} 25\)
- Contestar
-
1. \(4\)
2. \(-2\)
3. \(3\)
4. \(1\)
Ejercicio\(\PageIndex{23}\)
Esbozar la gráfica.
- \(f(x)=\log _{4}(x+5)+2\)
- \(f(x)=-\ln (x-2)\)
- Contestar
-
1.
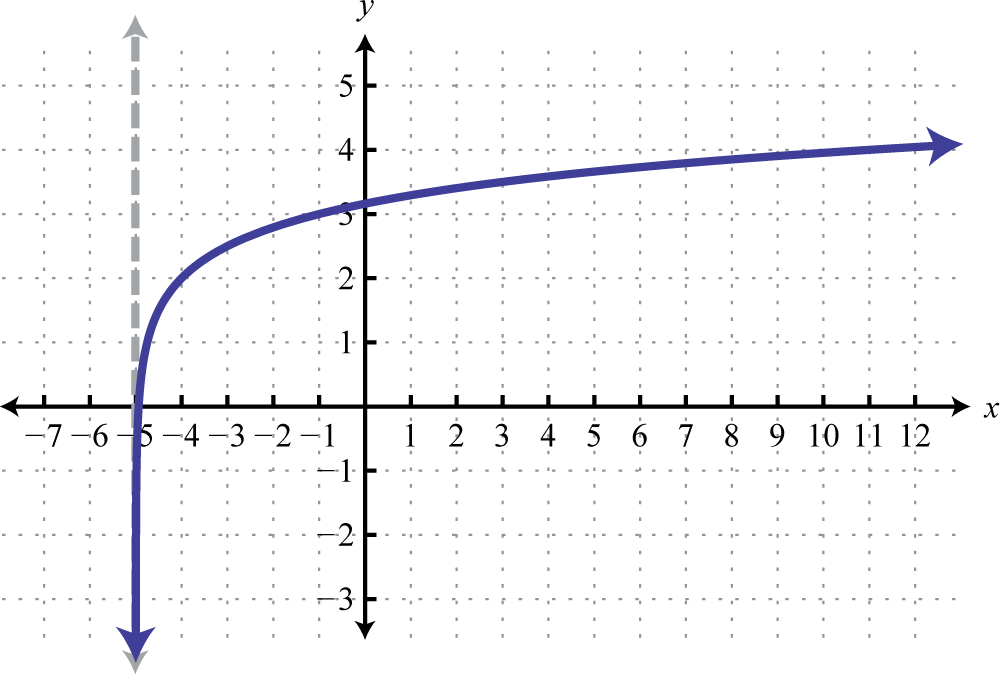
Figura 7.E.16
Ejercicio\(\PageIndex{24}\)
- Ampliar:\(\log \left(\frac{100 x^{2} y}{\sqrt{z}}\right)\).
- Escribir como un logaritmo único con coeficiente\(1\):\(2 \log _{2} x+\frac{1}{3} \log _{2} y-3 \log _{2} z\).
- Contestar
-
1. \(2+2 \log x+\log y-\frac{1}{2} \log z\)
Ejercicio\(\PageIndex{25}\)
Evaluar. Redondear a la décima más cercana.
- \(\log _{2} 10\)
- \(\ln 1\)
- \(\log _{3}\left(\frac{1}{5}\right)\)
- Contestar
-
1. \(3.3\)
2. \(0\)
3. \(-1.5\)
Ejercicio\(\PageIndex{26}\)
Resolver:
- \(2^{3 x-1}=16\)
- \(3^{7 x+1}=5\)
- \(\log _{5}(3 x-4)=\log _{5}(2 x+7)\)
- \(\log _{3}\left(x^{2}+26\right)=3\)
- \(\log _{2} x+\log _{2}(2 x+7)=2\)
- \(\log (2 x+3)=1+\log (x+1)\)
- Joe invirtió $\(5,200\) en una cuenta ganando\(3.8\)% de interés anual que se compone mensualmente. ¿Cuánto tiempo tardará en acumular un total de $\(6,200\) en la cuenta?
- Mary tiene $\(3,500\) en una cuenta de ahorro ganando\(4 \frac{1}{2}\)% de interés anual que se agrava continuamente. ¿Cuánto tiempo tardará en duplicar el monto en la cuenta?
- Durante la fase de crecimiento exponencial, ciertas bacterias pueden crecer a una tasa de\(5.3\)% por hora. Si\(12,000\) las células están inicialmente presentes en una muestra, construya un modelo de crecimiento exponencial y utilízalo para:
- Estimar la población de bacterias en\(3.5\) horas.
- Estimar el tiempo que tardará la población en duplicarse.
- La vida media del cesio-137 es de aproximadamente\(30\) años. Aproximar el tiempo que tomará una muestra de\(20\) -miligramo de cesio-137 para descomponerse a\(8\) miligramos.
- Contestar
-
2. \(\frac{\log 5-\log 3}{7 \log 3}\)
4. \(\pm 1\)
6. \(-\frac{7}{8}\)
8. \(15.4\)años
10. \(40\)años


