1.1: Una introducción a los enteros

Última actualización
Guardar como PDF

Page ID: 111550

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Comenzamos con el conjunto de números de conteo, formalmente llamado el conjunto de números naturales.

Los números naturales

El conjunto\[\mathbb{N}=\{1,2,3,4,5, \ldots \} \nonumber \] se llama el conjunto de números naturales.

Si agregamos el número cero al conjunto de números naturales, entonces tenemos un conjunto de números que se llaman los números enteros.

Los números enteros

El conjunto\[W=\{0,1,2,3,4,5, \ldots\} \nonumber \] se llama el conjunto de números enteros.

El número$0$ es especial, en que cada vez que lo agregas a otro número entero, obtienes el número idéntico como respuesta.

Propiedad de identidad aditiva

Si a es cualquier número entero, entonces\[a +0=a \nonumber \] Por esta razón, el número entero$0$ se llama la identidad aditiva.

Así, por ejemplo,$3 + 0 = 3$,$15 + 0 = 15$, y$123 + 0 = 123$. Todos estos son ejemplos de la propiedad aditiva de identidad. Cada número natural tiene un opuesto, de modo que cuando los sumas, su suma es cero.

Propiedad inversa aditiva

Si$a$ es algún número natural, entonces deﬁne lo contrario de$a$, simbolizado por$-a$, de modo que\[a +(-a)=0 \nonumber \] El número$-a$ se llame el “opuesto de$a$,” o más formalmente, el inverso aditivo de$a$.

Por ejemplo, lo opuesto (inverso aditivo) de$3$ es$−3$, y$3+(−3) = 0$. Lo opuesto (inverso aditivo) de$12$ es$−12$, y$12 + (−12) = 0$. Lo contrario de$254$ es$−254$, y$254+(−254) = 0$. Todos estos son ejemplos de inversas aditivas y la propiedad inversa aditiva.

Porque$7+(−7) = 0$, hemos dicho que$−7$ es lo opuesto (inverso aditivo) de$7$. No obstante, también podemos darle la vuelta a eso y decir que$7$ es lo contrario de$−7$. Si traducimos la frase “lo contrario de$−7$ es$7$” en símbolos matemáticos, obtenemos$−(−7) = 7$.

Lo contrario de lo contrario

Porque$a+(-a)=0,$ podemos decir que$a$ es lo contrario de$-a$. En símbolos, escribimos:\[-(-a)=a \nonumber \]

Así, por ejemplo,$-(-11)=11$,$-(-103)=103$, y$-(-1255)=1255$.

Los números enteros

Si recolectamos todos los números naturales y sus inversos aditivos, entonces incluimos el número cero, tenemos una colección de números llamados enteros.

Los números enteros

El conjunto\[\mathbb{Z}=\{\ldots,-5,-4,-3,-2,-1,0,1,2,3,4,5, \ldots\} \nonumber \] se llama el conjunto de enteros.

Los enteros se pueden hacer para que correspondan a puntos en una línea de una manera muy natural. Primero, dibuja una línea, luego localiza el número cero en cualquier lugar que desees. En segundo lugar, colocar el número uno a la derecha de cero. Esto determina la longitud de una unidad. Finalmente, localice los números$1,2,3,4,5, \dots$ a la derecha de cero, luego sus opuestos (inversas aditivas)$-1,-2,-3,-4,-5, \dots$ a la izquierda de cero (ver Figura$\PageIndex{1}$).

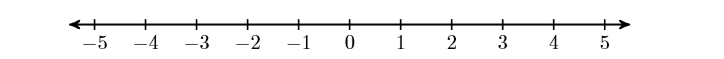
$higo 1.1.1.png$

Figura$\PageIndex{1}$: Cada entero corresponde a una posición única en la recta numérica.

Tenga en cuenta que a medida que nos movemos hacia la derecha en la recta numérica, los enteros se hacen más grandes. Por otro lado, a medida que nos movemos hacia la izquierda en la recta numérica, los enteros se hacen más pequeños.

Números enteros positivos y negativos

En la recta numérica, algunos enteros se encuentran a la derecha de cero y otros a la izquierda de cero.

Si$a$ es un entero que se encuentra a la derecha de cero, entonces$a$ se llama un entero positivo.
Si$a$ es un entero que se encuentra a la izquierda de cero, entonces$a$ se llama un entero negativo.

Así$4$,$25$, y$142$ son enteros positivos, while$-7$,$-53,$ y$-435$ son enteros negativos.

Valor Absoluto

El valor absoluto (o magnitud) de un entero se define de la siguiente manera.

El valor absoluto de un entero

Si$a$ es un entero, entonces el valor absoluto de$a$, escrito$|a|$, se establece como la distancia entre el entero y cero en la recta numérica.

Ejemplo$\PageIndex{1}$

Simplificar$|-4|$.

Solución

Considera la posición de$-4$ en la recta numérica. Tenga en cuenta que$-4$ se encuentra a cuatro unidades de distancia de cero.

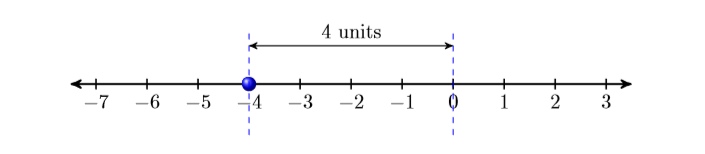
$higo 1.1.2.png$

Figura$\PageIndex{2}$

Debido a que el valor absoluto (magnitud) de un entero es igual a su distancia de cero,$|-4|=4$.

Ejercicio$\PageIndex{1}$

Simplificar:$|-23|$

Contestar: $|-23|=23$

De manera similar:

El entero$5$ se encuentra a cinco unidades de distancia de cero. De ahí,$|5|= 5$.
El entero$0$ se encuentra a cero unidades de distancia de cero, Por lo tanto,$|0|= 0$. Tenga en cuenta que el valor absoluto de cualquier número es positivo o cero. Es decir, el valor absoluto de un número es no negativo (no negativo).

Adición de enteros

Esta sección está diseñada para proporcionar una revisión rápida de la adición de enteros. Consideramos el primero de dos casos.

Agregar números enteros con signos similares

Para sumar dos enteros con signos similares (ambos positivos o ambos negativos), sumar sus magnitudes (valores absolutos), luego preﬁx su signo común.

Ejemplo$\PageIndex{2}$

Simplificar$7+12$.

Solución

Tenemos como señales. Las magnitudes (valores absolutos) de$7$ y$12$ son$7$ y$12$, respectivamente. Si sumamos las magnitudes, obtenemos$19$. Si preﬁx el signo común, obtenemos$19$. Es decir:\[7+12=19 \nonumber \]

Ejercicio$\PageIndex{2}$

Simplificar:$13+28$.

Contestar: $41$

Ejemplo$\PageIndex{3}$

Simplificar$-8+(-9)$.

Solución

Tenemos como señales. Las magnitudes (valores absolutos) de$-8$ y$-9$ son$8$ y$9$, respectivamente. Si sumamos las magnitudes, obtenemos$17$. Si preﬁx el signo común, obtenemos$-17$. Es decir:\[-8+(-9)=-17 \nonumber \]

Ejercicio$\PageIndex{3}$

Simplificar:$-12+(-21)$.

Contestar: $-33$

A continuación, consideramos el caso donde tenemos signos diferentes.

Agregar números enteros con signos de diferencia

Para sumar dos enteros con signos diferentes (uno positivo y otro negativo), restar el entero con la magnitud menor (valor absoluto) del número con la magnitud mayor, luego preﬁx el signo del entero con la magnitud mayor.

Ejemplo$\PageIndex{4}$

Simplificar$-14+11$.

Solución

Tenemos signos a diferencia. Las magnitudes (valores absolutos) de$-14$ y$11$ son$14$ y$11$, respectivamente. Si restamos la menor magnitud de la mayor, obtenemos$3$. El número$-14$ tiene la magnitud mayor, así que preﬁx nuestra respuesta con su signo negativo. Es decir:\[-14+11=-3 \nonumber \]

Ejercicio$\PageIndex{4}$

Simplificar:$12+(-29)$.

Contestar: $-17$

Ejemplo$\PageIndex{5}$

Simplificar$40+(-25)$.

Solución

Tenemos signos a diferencia. Las magnitudes (valores absolutos) de$40$ y$-25$ son$40$ y$25$, respectivamente. Si restamos la menor magnitud de la mayor, obtenemos$15$. El número$40$ tiene la magnitud mayor, así que preﬁx nuestra respuesta con su signo positivo. Es decir:\[40+(-25)=15 \nonumber \]

Ejercicio$\PageIndex{5}$

Simplificar:$32+(-90)$.

Contestar: $-58$

Propiedades matemáticas de la adición

El orden en que sumamos enteros no importa. Es decir,$-20 + 34$ da una respuesta idéntica a la suma$34 + (−20)$. En ambos casos, la respuesta es$14$. A este hecho se le llama la propiedad conmutativa de la adición.

La propiedad conmutativa de la adición

Si$a$ y$b$ son cualesquiera dos enteros, entonces:\[a+b=b+a \nonumber \]

A continuación, cuando sumamos tres enteros, no importa cuáles dos agreguemos primero. Por ejemplo, si sumamos primero el segundo y el tercero de tres números, obtenemos:

\[\begin{aligned}-11+(-2+5) &=-11+3 \quad {\color{Red} \text { Parentheses first: }-2+5=3} \\ &=-8 \quad {\color{Red} \text { Add: }-11+3=-8} \end{aligned} \nonumber \]

Por otro lado, si sumamos el primer y segundo de tres números primero, obtenemos:

\[\begin{aligned}(-11+(-2))+5 &=-13+5 \quad {\color{Red} \text { Parentheses first: }-11+(-2)=-13} \\ &=-8 \quad {\color{Red} \text { Add: }-13+5=-8} \end{aligned} \nonumber \]

Por lo tanto,$-11 + (−2 + 5) = (−11 + (−2)) + 5$. A este hecho se le llama la propiedad asociativa de la adición.

La propiedad asociativa de la adición

Si$a$,$b$, y$c$ son tres enteros cualquiera, entonces:\[a +( b + c)=( a + b)+c \nonumber \]

Resta de Enteros

La resta es la inversa, o lo contrario, de la suma.

Restar enteros

Si$a$ y$b$ son dos enteros cualesquiera, entonces:\[a-b = a +(-b) \nonumber \] Restar$b$ es idéntico a sumar lo opuesto (inverso aditivo) de$b$.

Ejemplo$\PageIndex{6}$

Simplificar:$-13-27$.

Solución

El “opuesto” (inverso aditivo) de$27$ es$-27$. Entonces, restar$27$ es lo mismo que sumar$-27$.

$\begin{aligned}-13-27&=-13+(-27) \quad {\color{Red} \text { Subtracting 27 is the same as adding −27.}} \\ &=-50 \quad {\color{Red} \text { Add the magnitudes, then prefix the common negative sign.}} \end{aligned}$

Ejercicio$\PageIndex{6}$

Simplificar:$-11-15$.

Contestar: $-26$

Ejemplo$\PageIndex{7}$

Simplificar:$-27-(-50)$.

Solución

El “opuesto” (inverso aditivo) de$-50$ es$-(-50)$, o$50$. Entonces, restar$-50$ es lo mismo que sumar$50$.

$\begin{aligned}-27-(-50)&=-27+50 \quad {\color{Red} \text { Subtracting -50 is the same as adding 50.}} \\&=23 \quad {\color{Red} \text { Subtract the smaller magnitude from the larger magnitude, then prefix the sign of the larger magnitude.}} \end{aligned}$

Ejercicio$\PageIndex{7}$

Simplificar:$-18-(-54)$.

Contestar: $36$

Multiplicación de Enteros

Esta sección está diseñada para proporcionar una revisión rápida de la multiplicación y división de enteros.

Como Signos

Si$a$ y$b$ son enteros con signos similares (ambos positivos o ambos negativos), entonces el producto$ab$ y el cociente$a/b$ son positivos.

\[\begin{array}{ll}{(+)(+)=+} \quad {\text { or }} & {(+) /(+)=+} \\ {(-)(-)=+\quad \text { or }} & {(-) /(-)=+}\end{array} \nonumber \]

Ejemplo$\PageIndex{8}$

Simplifica cada una de las siguientes expresiones:

$(2)(3)$
$(-12)(-8)$
$-14 /(-2)$

Solución

Al multiplicar o dividir, los signos similares producen un resultado positivo.

$(2)(3)=6$
$(-12)(-8)=96$
$-14 /(-2)=7$

Ejercicio$\PageIndex{8}$

Simplificar:$(-18)(-5)$.

Contestar: $90$

A diferencia de los signos

Si$a$ y$b$ son enteros con signos distintos (uno positivo y otro negativo), entonces el producto$ab$ y el cociente$a/b$ son negativos.

\[\begin{array}{ll}{(+)(-)=-} & {\text { or }}& {(+) /(-)=-} \\ {(-)(+)=-} & {\text { or }} & {(-) /(+)=-}\end{array} \nonumber \]

Ejemplo$\PageIndex{9}$

Simplifica cada una de las siguientes expresiones:

$(2)(-12)$
$(-9)(12)$
$24/(-8)$

Solución

Al multiplicar o dividir, a diferencia de los signos arrojan un resultado negativo.

$(2)(-12)=-24$
$(-9)(12)=-108$
$24 /(-8)=-3$

Ejercicio$\PageIndex{9}$

Simplificar:$(-19)(3)$.

Contestar: $-57$

Propiedades matemáticas de la multiplicación

El orden en que multiplicamos los enteros no importa. Es decir,$(-8)(5)$ da una respuesta idéntica a$(5)(-8)$. En ambos casos, la respuesta es$-40$. Este hecho se llama la propiedad conmutativa de la multiplicación.

La propiedad conmutativa de la multiplicación

Si$a$ y$b$ son cualesquiera dos enteros, entonces:\[a \cdot b=b+a \nonumber \]

A continuación, cuando multiplicamos tres enteros, no importa cuáles dos multipliquemos primero. Si multiplicamos primero el segundo y el tercero de tres números, obtenemos:

\[\begin{aligned}(-3)[(-4)(-5)] &=(-3)(20) & {\color{Red} \text { Brackets first: }(-4)(-5)=20} \\ &=-60 & {\color{Red} \text { Multiply: }(-3)(20)=-60} \end{aligned} \nonumber \]

Por otro lado, si multiplicamos el primer y segundo de tres números primero, obtenemos:

\[\begin{aligned}[(-3)(-4)](-5)&=(12)(-5) & {\color{Red} \text { Brackets first: }(-3)(-4)=12} \\ & =-60 & {\color{Red} \text { Multiply: }(12)(-5)=-60}\end{aligned} \nonumber \]

Por lo tanto,$(-3)[(-4)(-5)]=[(-3)(-4)](-5)$. Este hecho se llama la propiedad asociativa de la multiplicación.

La propiedad asociativa de la multiplicación

Si$a$,$b$, y$c$ son tres enteros cualquiera, entonces:\[a \cdot(b \cdot c)=(a \cdot b) \cdot c \nonumber \]

Cuando multiplicas un número entero por$1$, obtienes el número idéntico al del producto. Por ejemplo,$(1)(5) = 5$ y$(-11)(1) = -11$. Este hecho se conoce como la propiedad de identidad multiplicativa.

La propiedad de identidad multiplicativa

Si a es cualquier entero, entonces:\[1 \cdot a=a \quad \text { and } \quad a \cdot 1=a \nonumber \] Por esta razón, el entero$1$ se llama la “identidad multiplicativa”.

Por último, tenga en cuenta que$(-1)(5) = -5$. Así, multiplicar$5$ por$-1$ es idéntico a tomar lo “opuesto” de$5$ o negar$5$.

La propiedad multiplicativa de$−1$

Multiplicar por menos uno es idéntico a negar. Es decir:\[(-1) a=-a \nonumber \]

Exponentes

En la expresión exponencial$a^n$, el número$a$ se llama la base, mientras que el número$n$ se llama exponente. Ahora deﬁne lo que se entiende por exponente.

Exponentes

Dejar$a$ ser un entero y dejar$n$ ser cualquier número entero. Si$n \neq 0$, entonces:\[a^{n}=\underbrace{a \cdot a \cdot a \cdot \cdots \cdot a}_{n \text { times }} \nonumber \]

Es decir, para calcular$a^n$, escribir$a$ como factor$n$ tiempos.

Ejemplo$\PageIndex{10}$

Simplificar$(-2)^{3}$.

Solución

En la expresión exponencial$(-2)^3$, nótese que$-2$ es la base, mientras que$3$ es el exponente. El exponente nos dice que escribamos la base como factor tres veces. Simplifica el resultado realizando las multiplicaciones en orden, moviéndose de izquierda a derecha.

\[\begin{aligned}(-2)^{3} & =(-2)(-2)(-2)\quad {\color{Red}\text { -2 as a factor, three times.}} \\ & =(4)(-2)\quad {\color{Red}\text { Multiply: (-2)(-2)=4}} \\ & =-8 \quad {\color{Red}\text { Multiply: (4)(-2)=-8}}\\ \text{Thus } (-2)^{3} &=-8\end{aligned} \nonumber \]

Ejercicio$\PageIndex{10}$

Simplificar:$(-2)^{2}$.

Contestar: $4$

En Ejemplo $\PageIndex{10}$, tenga en cuenta que el producto de tres factores negativos es negativo. Intentemos otro ejemplo.

Ejemplo$\PageIndex{11}$

Simplificar$(-2)^{4}$.

Solución

En la expresión exponencial$(-2)4$, nótese que$-2$ es la base, mientras que$4$ es el exponente. El exponente nos dice que escribamos la base como factor cuatro veces. Simplifica el resultado realizando las multiplicaciones en orden, moviéndose de izquierda a derecha.

\[\begin{aligned}(-2)^{4} & =(-2)(-2)(-2)(-2)\quad {\color{Red}\text { -2 as a factor, four times.}} \\ & =(4)(-2)(-2)\quad {\color{Red}\text { Multiply: (-2)(-2)=4}} \\ & =(-8)(-2) \quad {\color{Red}\text { Multiply: (4)(-2)=-8}}\\ & = 16 \quad {\color{Red}\text { Multiply: (-8)(-2)=-8}}\\ \text{Thus } (-2)^{4} &=16\end{aligned} \nonumber \]

Ejercicio$\PageIndex{11}$

Simplificar:$(-2)^{5}$.

Contestar: $-32$

En Ejemplo $\PageIndex{11}$, tenga en cuenta que el producto de cuatro factores negativos es positivo. Ejemplos $\PageIndex{10}$y $\PageIndex{11}$revelan el siguiente patrón.

Exponentes impares o impares

Cuando un entero negativo se eleva a un exponente par, el resultado es positivo.
Cuando un entero negativo se eleva a un exponente impar, el resultado es negativo.

Calculadora gráfica: negar versus restar

$higo 1.1.3.png$

Figura$\PageIndex{3}$: Mitad inferior del TI-84.

Considere la vista de la mitad inferior de la calculadora gráfica TI-84 en la Figura$\PageIndex{3}$. Tenga en cuenta que hay dos claves que contienen algún tipo de signo negativo, una en la fila inferior de teclas, y otra en la última columna de teclas a la derecha, posicionadas justo encima del símbolo más.

$higo 1.1.4.png$

Figura$\PageIndex{4}$

El primero de estos botones es el operador unario de “negación”. Si quieres negar un solo número (de ahí la palabra “unario”), entonces esta es la clave a usar. Por ejemplo, ingrese$-3$ presionando la siguiente secuencia de botones. El resultado se muestra en la Figura$\PageIndex{7}$.

$higo 1.1.5.png$

Figura$\PageIndex{5}$

El segundo botón es el operador binario de “resta”. Si quieres restar un número de otro número (de ahí la palabra “binario”), entonces esta es la clave a usar. Por ejemplo, ingrese$7-15$ presionando la siguiente secuencia de botones. El resultado se muestra en la Figura$\PageIndex{8}$.

$higo 1.1.6.png$

Figura$\PageIndex{6}$

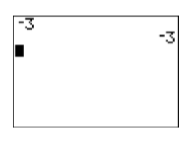
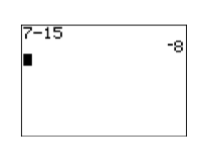
$higo 1.1.7.png$ $higo 1.1.8.png$

Figura$\PageIndex{7}$: Negando un número. Figura$\PageIndex{8}$: Restar dos números.

Nota

No intercambiar los roles del operador de negación unaria y el operador de resta binaria.

Para negar un número, use: (-)
Para restar un número de otro, use: −

Si cambias los roles de estos operadores, la calculadora responderá que has cometido un “error de sintaxis” (ver Figuras$\PageIndex{9}$ y$\PageIndex{10}$).

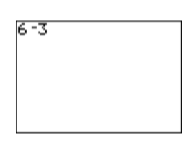
$higo 1.1.9.png$ $higo 1.1.10.png$

Figura$\PageIndex{9}$: Usar el símbolo incorrecto para restar. Figura$\PageIndex{10}$: El error de sintaxis resultante.

Ejemplo$\PageIndex{12}$

Utilice la calculadora gráfica TI-84 para simplificar cada una de las siguientes expressons:

$-717-432$
$(232)(-313)$
$(-17)^{3}$

Solución

El signo menos en cada uno de estos ejemplos se ve exactamente igual, pero a veces se usa como signo “negativo” y a veces se usa como signo de “resta”.

La expresión nos$-717-432$ pide restar$432$ de “negativo”$717$. Ingrese la siguiente secuencia de pulsaciones de teclas para producir el resultado que se muestra en la primera imagen de la Figura$\PageIndex{11}$.

$fig 1.1.11a.png$

De ahí,$-717-432=-1149$.

La expresión nos$(232)(-313)$ pide encontrar el producto de$232$ y “negativo”$313$. Ingrese la siguiente secuencia de pulsaciones de teclas para producir el resultado mostrado en la segunda imagen de la Figura$\PageIndex{11}$.

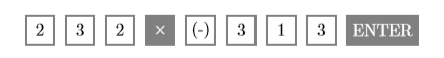
$fig 1.1.11b.png$

De ahí,$(232)(-313)=-72616$.

La expresión nos$(-17)^3$ pide elevar “negativo” al tercer poder. Ingrese la siguiente secuencia de pulsaciones de teclas para producir el resultado mostrado en la tercera imagen de la Figura$\PageIndex{11}$. El símbolo ^ de “intercalación” se encuentra justo encima de la clave de división en la columna más a la derecha de la calculadora gráfica TI-84.

$higo 1.1.11c.png$

De ahí,$(-17)^{3}=-4913$.

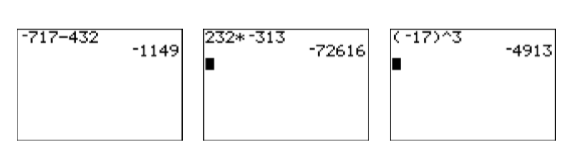
$higo 1.1.11.png$

Figura$\PageIndex{11}$: Cálculos realizados en la calculadora gráfica.

Ejercicio$\PageIndex{12}$

Utilice la calculadora gráfica para evaluar$(-225)^3$.

Contestar: $(-225)^3 = -11390625$

Colaboradores

Template:ContribElemAlgebraArnold