1.2: Orden de Operaciones

Última actualización
Guardar como PDF

Page ID: 111571

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

El orden en que evaluamos las expresiones puede ser ambiguo. Tomemos, por ejemplo, la expresión$-4+2 \cdot 8$. Si realizamos la primera suma, entonces obtenemos$-16$ como resultado (el signo de interrogación sobre el signo igual indica que el resultado es cuestionable).

\[\begin{align*} -4+2 \cdot 8 &\overset{?}{=} -2 \cdot 8\\ &\overset{?}{=}-16 \end{align*} \nonumber \]

Por otro lado, si realizamos la primera multiplicación, entonces obtenemos$12$ como resultado.

\[\begin{align*} -4+2 \cdot 8 &\overset{?}{=} -4 + 16\\ &\overset{?}{=}12 \end{align*} \nonumber \]

Entonces, ¿qué vamos a hacer? Por supuesto, agrupar símbolos eliminaría la ambigüedad.

Agrupación de símbolos

Se pueden usar paréntesis, corchetes y barras de valor absoluto para agrupar partes de una expresión. Por ejemplo:

\[3+5(9-11) \quad \text{or} \quad-2-[-2-5(1-3)] \quad \text{or} \quad 6-3|-3-4| \nonumber \]

En cada caso, la regla es “evaluar la expresión dentro de los símbolos de agrupación primero”. Si los símbolos de agrupación están anidados, evalúe la expresión en el par más interno de símbolos de agrupación primero.

Así, si el ejemplo anterior se agrupa de la siguiente manera, nos vemos obligados a evaluar la expresión dentro de los paréntesis primero.

\[\begin{aligned} (-4+2) \cdot 8 &=-2 \cdot 8 \color{Red}\text { Parentheses first: }-4+2=-2 \\ &=-16 \quad \color{Red} \text { Multiply: }-2 \cdot 8=-16 \end{aligned} \nonumber \]

Otra forma de evitar ambigüedades en la evaluación de expresiones es establecer un orden en el que deben realizarse las operaciones. Siempre se deben aplicar estrictamente las siguientes pautas a la hora de evaluar expresiones.

Reglas que guían el orden de operaciones

Al evaluar expresiones, proceda en el siguiente orden.

Evalúe las expresiones contenidas en los símbolos de agrupación primero. Si los símbolos de agrupación están anidados, evalúe la expresión en el par más interno de símbolos de agrupación primero.
Evaluar todos los exponentes que aparecen en la expresión.
Realizar todas las multiplicaciones y divisiones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.
Realizar todas las sumas y restaciones en el orden en que aparezcan en la expresión, moviéndose de izquierda a derecha.

Ejemplo$\PageIndex{1}$

Simplificar:$-3-4 \cdot 8$.

Solución

Debido a las Reglas establecidas que rigen el orden de operaciones, esta expresión ya no es ambigua. No hay símbolos de agrupación ni exponentes presentes, por lo que inmediatamente vamos a la regla tres, evaluamos todas las multiplicaciones y divisiones en el orden en que aparecen, moviéndonos de izquierda a derecha. Después de eso invocamos la regla cuatro, realizando todas las adiciones y restas en el orden en que aparecen, moviéndonos de izquierda a derecha.

\[\begin{aligned} -3-4 \cdot 8&= -3-32 \quad \color{Red} \text { Multiply first: } 4 \cdot 8=32 \\ &= -3+(-32) \quad \color{Red} \text { Add the opposite. } \\ &= -35 \quad \color{Red} \text { Add: }-3+(-32)=-35\\ \text{Thus, } -3-4 \cdot 8&= -35 \end{aligned} \nonumber \]

Ejercicio$\PageIndex{1}$

Simplificar:$-4+2 \cdot 8$.

Contestar: $12$

Redacción Matemáticas

Al simplificar expresiones, observe la siguiente regla para organizar cuidadosamente su trabajo:
Un signo igual por línea.

Esto significa que no debes organizar tu trabajo horizontalmente.

\[-2-4 \cdot(-8)=-2-(-32)=-2+32=30 \nonumber \]

Eso son tres signos iguales en una sola línea. Más bien, organice su trabajo verticalmente, manteniendo los signos iguales alineados en una columna.

\[\begin{aligned}-2-4 \cdot(-8) &=-2-(-32) \\ &=-2+32 \\ &=30 \end{aligned} \nonumber \]

Ejemplo$\PageIndex{2}$

Simplificar:$54/(-9)(2)$.

Solución

No hay símbolos de agrupación ni exponentes presentes, por lo que inmediatamente vamos a la regla tres, evaluamos todas las multiplicaciones y divisiones en el orden en que aparecen, moviéndonos de izquierda a derecha.

\[\begin{aligned} 54 /(-9)(2) &=-6(2) \quad \color{Red}\text { Divide first: } 54 /(-9)=-6 \\ &=-12 \quad \color{Red}\text { Multiply: }-6(2)=-12 \\ \text{Thus, } 54 /(-9)(2)&= -12 \end{aligned} \nonumber \]

Ejercicio$\PageIndex{2}$

Simplificar:$-24 /(-3)(2)$.

Contestar: $16$

El ejemplo $\PageIndex{2}$puede ser fuente de confusión para muchos lectores. Tenga en cuenta que la multiplicación no toma preferencia sobre la división, ni la división toma preferencia sobre la multiplicación. Las multiplicaciones y divisiones tienen el mismo nivel de preferencia y deben realizarse en el orden en que ocurran, moviéndose de izquierda a derecha. De no ser así, se obtendrá la respuesta equivocada.

$\color{Red}\text {Warning!}$

Esto es lo que sucede si realizas la multiplicación en Ejemplo $\PageIndex{2}$antes de la división.

\[\begin{aligned} 54 /(-9)(2) &=54/(-18) \quad \color{Red}\text { Multiply: } (-9)(2)=-18 \\ &=-3 \quad \color{Red}\text { Divide: } 54/(-18)=-3 \end{aligned} \nonumber\]

$\color{Red}\text{This is incorrect!}$Las multiplicaciones y divisiones deben realizarse en el orden en que ocurran, moviéndose de izquierda a derecha.

Ejemplo$\PageIndex{3}$

Simplificar:

$(-7)^{2}$
$-7^{2}$

Solución

Recordemos que para cualquier entero a, tenemos$(-1)a =-a$. Debido a que negar equivale a multiplicar por$-1$, el Orden de Operaciones Rector de Reglas requiere que abordemos los símbolos de agrupación y exponentes antes de la negación.

Debido a los símbolos de agrupación, negamos primero, luego cuadrado. Es decir,\[\begin{aligned}(-7)^{2} &=(-7)(-7) \\ &=49 \end{aligned} \nonumber \]
No hay símbolos de agrupación en este ejemplo. Así, debemos cuadrar primero, luego negar. Es decir,\[\begin{aligned}-7^{2} &=-(7 \cdot 7) \\ &=-49 \end{aligned} \nonumber \]

Así,$(-7)^2 = 49$, pero$-7^2 = -49$. Nota: Este ejemplo demuestra que$(-7)^2$ es diferente de$-7^2$.

Ejercicio$\PageIndex{3}$

Simplificar:$-15^{2}$.

Contestar: $-225$

Probemos un ejemplo que tenga una mezcla de exponentes, multiplicación y resta.

Ejemplo$\PageIndex{4}$

Simplificar:$-3-2(-4)^{2}$.

Solución

El Orden de Operaciones Rector de Reglas requiere que abordemos exponentes primero, luego multiplicaciones, luego restaciones.

\[\begin{aligned} -3-2(-4)^{2} &=-3-2(16) \quad \color{Red} \text{ Exponent first: } (-4)^2 = 16 \\ &=-3-32 \quad \color{Red} \text{ Multiply: } 2(16)=32 \\ &=-3+(-32) \quad \color{Red} \text{Add the opposite.} \\ &=-35 \quad \color{Red} \text{ Add: } -3+(-32) = -35 \\ \text{Thus, } -3-2(-4)^{2} &= -35 \end{aligned} \nonumber \]

Ejercicio$\PageIndex{4}$

Simplificar:$-5-4(-2)^{3}$.

Contestar: $27$

Agrupación de símbolos

El orden de operaciones de guía de reglas requiere que las expresiones dentro de los símbolos de agrupación (paréntesis, corchetes o llaves) se evalúen primero.

Ejemplo$\PageIndex{5}$

Simplificar:$-2(3-4)^{2}+5(1-2)^{3}$.

Solución

El Orden de Operaciones Rector de Reglas requiere que primero evaluemos las expresiones contenidas dentro de los símbolos de agrupación.

\[\begin{aligned} -2(3-4)^{2} + 5(1-2)^{3} &=-2(3+(-4))^{2}+5(1+(-2))^{3} \quad \color{Red} \text{ Add the opposites.}\\ &=-2(-1)^{2}+5(-1)^{3} \quad \color{Red} \text{ Parenthesis first: } 3+(-4)=-1 \text{ and } 1+(-2)=-1\\ \text {Evaluate the exponents next, perform the multiplications, then add.}\\ &= -2(1)+5(-1) \quad \color{Red} \text{ Exponents: } (-1)^2=1 \text{ and } (-1)^3=-1\\ &=-2(1)+5(-1) \quad \color{Red} \text{ Multiply: } -2(1)=-2 \text{ and } 5(-1)=-5 \\ &=-7 \quad \color{Red} \text{ Add } -2+(-5)=-7 \\ \text{Thus, } -2(3-4)^{2} + 5(1-2)^{3} &= -7 \end{aligned}\nonumber\]

Ejercicio$\PageIndex{5}$

Simplificar:$-2-3(-2-3)^{3}$.

Contestar: $373$

Barras de valores absolutos como símbolos de agrupación

Al igual que los paréntesis y corchetes, debes evaluar primero lo que hay dentro de ellos, luego tomar el valor absoluto del resultado.

Ejemplo$\PageIndex{6}$

Simplificar:$-8-|5-11|$.

Solución

Primero debemos evaluar lo que hay dentro de las barras de valor absoluto.

\[\begin{aligned} -8-|5-11| &=-8-|5+(-11)| \quad \color{Red} \text{ Add the opposites.}\\ &=-8-|-6| \quad \color{Red} \text{ Add: } 5+(-11)=-6\\ \text {The number } -6 \text{ is } 6 \text{ units from zero on the number line. Hence, } |-6|=6 \\ &= -8-6 \quad \color{Red} \text{ Add: } |-6|=6\\ &= -8+(-6) \quad \color{Red} \text{ Add the opposite. } \\ &=-14 \quad \color{Red} \text{ Add. } -2+(-5)=-7 \\ \text{Thus, } -8-|5-11| &= -14 \end{aligned}\nonumber\]

Ejercicio$\PageIndex{6}$

Simplificar:$-|-4-6|$.

Contestar: $-10$

Símbolos de agrupación anidada

Cuando se anidan los símbolos de agrupación, el Orden de Operaciones de Guía de Reglas nos dice que evaluemos primero las expresiones más internas.

Ejemplo$\PageIndex{7}$

Simplificar:$-3-4[-3-4(-3-4)]$.

Solución

El orden rector de las operaciones de reglas requiere que primero abordemos la expresión contenida en los símbolos de agrupación más internos. Es decir, evaluamos la expresión contenida dentro de los corchetes primero.

\ [\ begin {alineado}
-3-4 [-3-4 (-3-4)] &=-3-4 [-3-4 (-3+ (-4))]\ quad\ color {Rojo}\ texto {Agrega lo contrario.} \\
&=-3-4 [-3-4 (-7)]\ quad\ color {Rojo}\ texto {Agregar:} -3+ (-4) =-7\\
\ text {A continuación, evaluamos la expresión contenida dentro de los corchetes.}\\
&= -3-4 [-3- (-28)]\ quad\ color {Rojo}\ text {Multiplicar:} 4 (-7) =-28\\
&= -3-4 [-3+28]\ quad\ color {Rojo}\ text {Agrega lo contrario.}\\
&= -3-4 [25]\ quad\ color {Rojo}\ texto {Agregar:} -3+28=25\\
\ text {Ahora multiplicamos, luego restamos.} \\
&= -3-100\ quad\ color {Rojo}\ texto {Multiplicar:} 4\ {25\} =100\\
&= -3+ (-100)\ quad\ color {Rojo}\ texto {Agrega lo contrario.}\\
&= -103\ quad\ color {Rojo}\ texto {Agregar:} -3+ (-100) =-103\\
\ texto {Así,} -3-4 [-3-4 (-3-4)] &= -103\ end {alineado} \ nonumber\]

Ejercicio$\PageIndex{7}$

Simplificar:$-2-2[-2-2(-2-2)]$.

Contestar: $-14$

Evaluación de expresiones algebraicas

Variable

Una variable es un símbolo (generalmente una letra) que representa un valor desconocido que puede variar.

Agreguemos la definición de una expresión algebraica.

Expresión algebraica

Cuando combinamos números y variables de manera válida, utilizando operaciones como suma, resta, multiplicación, división, exponenciación, la combinación resultante de símbolos matemáticos se denomina expresión algebraica.

Por lo tanto,

\[2a, \quad x+5, \quad \text{and} \quad y^{2} \nonumber \]

estando formados por una combinación de números, variables y operadores matemáticos, son expresiones algebraicas válidas.

Una expresión algebraica debe estar bien formada. Por ejemplo, no\[2+-5x \nonumber \] es una expresión válida porque no hay término que siga al signo más (no es válido escribir$+−$ sin nada entre estos operadores). Del mismo modo, no\[2+3(2 \nonumber \] está bien formado porque los paréntesis no están equilibrados.

En esta sección evaluaremos expresiones algebraicas para valores dados de las variables contenidas en las expresiones. A continuación te presentamos algunos consejos simples para ayudarte a tener éxito.

Consejos para evaluar expresiones algebraicas

Reemplazar todas las ocurrencias de variables en la expresión con paréntesis abiertos. Dejar espacio entre paréntesis para sustituir el valor dado de la variable.
Sustituir los valores dados de las variables en los paréntesis abiertos preparados en el primer paso.
Evaluar la expresión resultante de acuerdo con el Orden de Operaciones Rector de Reglas.

Ejemplo$\PageIndex{8}$

Evaluar la expresión$x^{2}-2xy+y^{2}$ en$x=-3$ y$y=2$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplazará todas las ocurrencias de variables en la expresión$x^{2}-2xy+y^{2}$ con paréntesis abiertos. A continuación, sustituya los valores dados de las variables ($-3$$2$para$x$ y para$y$) entre paréntesis abiertos.

\[\begin{aligned} x^{2}-2 x y+y^{2} &=(\;\; )^{2}-2(\;\;)( )+( )^{2} \\ &=({\color{Red}-3})^{2}-2({\color{Red}-3})({\color{Red}2})+({\color{Red}2})^{2} \end{aligned} \nonumber \]

Por último, seguir las Reglas Orientadoras Orden de Operaciones para evaluar la expresión resultante.

\[\begin{aligned} x^{2} &-2 x y+y^{2} \quad \color{Red} \text{ Original Expression. } \\ &=(\;\;)^{2}-2(\;\;)()+()^{2} \quad \color{Red} \text{ Replace variables with parenthesis. } \\ &=({\color{Red}-3})^{2}-2({\color{Red}-3})({\color{Red}2})+({\color{Red}2})^{2} \quad \color{Red} \text{ Substitute } -3 \text{ for } x \text{ and } 2 \text{ for } y \\ &=9-2(-3)(2)+4 \quad \color{Red} \text{ Evaluate exponenets first. } \\ &=9-(-6)(2)+4 \quad \color{Red} \text{ Left to right, multiply: } 2(-3)=-6\\ &=9-(-12)+4 \quad \color{Red} \text{ Left to right, multiply: } (-6)2=-12\\ &=9+12+4 \quad \color{Red} \text{ Add the opposite. } \\ &=25 \quad \color{Red} \text{ Add. }\\ \text{Thus, if } x=-3 \text{ and } y=2 \text{ , then } x^{2}-2 x y+y^{2}=25 \end{aligned} \nonumber\]

Ejercicio$\PageIndex{8}$

Si$x=-2$ y$y=-1$, evaluar$x^{3}-y^{3}$.

Contestar: $-7$

Evaluando Fracciones

Si hay una barra de fracciones, evalúe el numerador y el denominador por separado de acuerdo con el Orden de Operaciones Rector de Reglas, luego realice la división en el paso final.

Ejemplo$\PageIndex{9}$

Evaluar la expresión\[\dfrac{ad-bc}{a+b} \nonumber\] en$a=5, b=-3, c=2,$ y$d=-4$.

Solución

Siguiendo Consejos para evaluar expresiones algebraicas, primero reemplazará todas las ocurrencias de variables en la expresión$(ad−bc)/(a+b)$ con paréntesis abiertos. A continuación, sustituya los valores dados de las variables ($5$$-3$for$a$$b$,$2$ for$c$,$-4$ for y for$d$) entre paréntesis abiertos.

\[\begin{aligned} \dfrac{a d-b c}{a+b} &=\dfrac{(x)-(x)}{( )+( )} \\ &=\dfrac{({\color{Red}5})({\color{Red}-4}-)-({\color{Red}-3})({\color{Red}2})}{({\color{Red}5})+({\color{Red}-3})} \end{aligned} \nonumber\]

Por último, seguir las Reglas Orientadoras Orden de Operaciones para evaluar la expresión resultante. Tenga en cuenta que evaluamos las expresiones en el numerador y denominador por separado, luego dividimos.

\ [\ begin {alineado}
\ dfrac {a d-b c} {a+b} &=\ dfrac {(x) - (x)} {() + ()}\ quad\ color {Rojo}\ texto {Reemplazar variables con paréntesis.}\\
&=\ dfrac {({\ color {Rojo} 5}) ({\ color {Rojo} -4} -) - ({\ color {Rojo} -3}) ({\ color {Rojo} 2})} {({\ color {Rojo} 5}) + ({\ color {Rojo} -3})}\ quad\ color {Rojo}\ texto { Sustituto:} 5\ texto {para} a, -3\ texto {para} b, 2\ texto {para} c, -4\ texto {para} d\\
&=\ dfrac {-20- (-6)} {2}\ quad\ color {Rojo}\ texto {Numerador:} (5) (-4) =-20, (-3) (2) =-6\ texto {, Denominador:} 5+ (-3) =2\\
&=\ dfrac {-20+6} {2}\ quad\ color {Rojo}\ texto {Numerador: Añadir el opuesto.}\\
&=\ dfrac {-14} {2}\ quad\ color {Rojo}\ texto {Numerador:} -20+6=-14\\
&=-7\ quad\ color {Rojo}\ texto {Divide}\
\ texto {Así, si} x=-3\ texto {y} y=2\ texto {, entonces} x^ {2} -2 x y+y^ {2} =25
\ final {alineado}\ nonumber\]

Ejercicio$\PageIndex{9}$

Si$a=-7, b=-3, c=-15$ y$d=-14$, evaluar:$\dfrac{a^{2}+b^{2}}{c+d}$

Contestar: $-2$

Uso de la Calculadora Gráfica

La calculadora gráfica es una herramienta espléndida para evaluar expresiones algebraicas, particularmente cuando los números involucrados son grandes.

Ejemplo$\PageIndex{10}$

Utilice la calculadora gráfica para simplificar la siguiente expresión:\[-213-35[-18-211(15-223)] \nonumber \]

Solución

La primera dimensión con esta expresión es el hecho de que la calculadora gráfica no tiene un símbolo de corchete para fines de agrupación. La calculadora sólo tiene paréntesis para agrupar. Entonces primero convertimos nuestra expresión a lo siguiente:

\[-213-35(-18-211(15-223)) \nonumber \]

Tenga en cuenta que los corchetes y paréntesis son completamente intercambiables La siguiente dimensión es determinar cuáles de los signos menos son símbolos de negación y cuáles son símbolos de resta. Si el signo menos no aparece entre dos números, es un símbolo de negación. Si el signo menos aparece entre dos números, es un símbolo de resta. De ahí que ingresemos las siguientes pulsaciones de teclas en nuestra calculadora. El resultado se muestra en la Figura$\PageIndex{1}$.

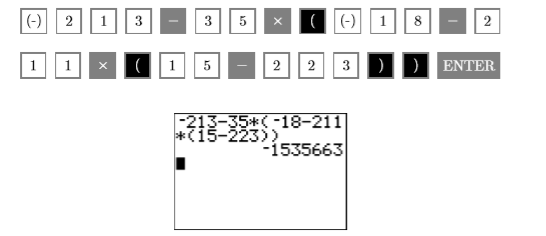
$higo 1.2.1.png$

Figura$\PageIndex{1}$: Cálculo$-213-35[-18-211(15-223)]$

Por lo tanto,$-213-35[-18-211(15-223)]=-1,535,663$.

Ejercicio$\PageIndex{10}$

Utilice la calculadora gráfica para evaluar:\[-2-2[-2-2(-2-2)] \nonumber \]

Contestar: $-14$

Ejemplo$\PageIndex{11}$

Utilice la calculadora gráfica para evaluar:\[\dfrac{5+5}{5+5} \nonumber \]

Solución

Podrías preguntar “¿Por qué necesitamos una calculadora para evaluar esta expresión sumamente simple?” Después de todo, es muy fácil de calcular.

\[\begin{aligned} \dfrac{5+5}{5+5} &=\dfrac{10}{10} \quad \color{Red} \text{ Simplify numerator and denominator. } \\ &=1 \quad \color{Red} \text{ Divide: } 10/10=1 \end{aligned} \nonumber \]

Bueno, ingresemos la expresión$5+5/5+5$ en la calculadora y veamos qué tan bien entendemos el Orden de Operaciones de Guía de Reglas (ver primera imagen en la Figura$\PageIndex{2}$). ¡Whoa! ¿Cómo llegó la calculadora$11$? ¡Se supone que la respuesta es$1$! Disminuyamos la velocidad y apliquemos a la expresión las Reglas que orientan el orden de operaciones$5+5/5+5$.

\[\begin{aligned} \dfrac{5+5}{5+5} &= 5+\dfrac{5}{5}+5 \quad \color{Red} \text{ Divide first. } \\ &=5+1+5 \quad \color{Red} \text{ Divide: } \dfrac{5}{5}=1 \\ &= 11 \quad \color{Red} \text{ Add: } 5+1+5=11 \end{aligned} \nonumber \]

¡Ajá! Así es como se puso la calculadora$11$.

\[5+5 / 5+5 \quad \text { is equivalent to } \quad 5+\dfrac{5}{5}+5 \nonumber \]

Cambiemos el orden de evaluación mediante el uso de símbolos de agrupación. Tenga en cuenta que:

\[\begin{aligned} (5+5) /(5+5) &=10 / 10 \quad \color{Red} \text { Parentheses first. } \\ &= 1 \quad \color{Red} \text { Divide: } 10/10 = 1 \end{aligned} \nonumber \]

Es decir:

\[(5+5) /(5+5) \quad \text { is equivalent to } \quad \dfrac{5+5}{5+5} \nonumber \]

Entrar$(5+5)(5+5)$ y presionar la tecla ENTER para producir la salida que se muestra en la segunda imagen de la Figura$\PageIndex{2}$).

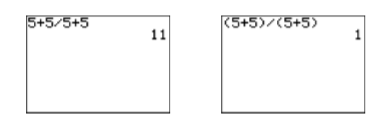
$higo 1.2.2.png$

Figura$\PageIndex{2}$): Cálculo$\dfrac{5+5}{5+5}$

Ejercicio$\PageIndex{11}$

Utilice la calculadora gráfica para evaluar:\[\dfrac{10+10}{10+10} \nonumber \]

Contestar: $1$

La calculadora gráfica tiene ubicaciones de memoria disponibles para “almacenar” valores. Están rotuladas de la A a la Z y aparecen en la caja de la calculadora, en orden alfabético a medida que te mueves de izquierda a derecha y bajando por el teclado. Almacenar valores en estas ubicaciones de memoria es una forma eficiente de evaluar expresiones algebraicas que contienen variables. Utilice la tecla ALPHA para acceder a estas ubicaciones de memoria.

$higo 1.2.3.png$

Figura$\PageIndex{3}$): Mitad superior del TI-84.

Ejemplo$\PageIndex{12}$

Utilice la calculadora gráfica para evaluar$|a|-|b|$ en$a=-312$ y$b=-875$.

Solución

Primero almacene$-312$ en la variable$A$ con las siguientes pulsaciones de teclas. Para seleccionar la letra$A$, presione la tecla ALPHA, luego la tecla MATH, ubicada en la esquina superior izquierda de la calculadora (ver Figura$\PageIndex{3}$).

$higo 1.2.5a.png$

A continuación, almacene$-875$ en la variable B con las siguientes pulsaciones de teclas. Para seleccionar la letra$B$, presione la tecla ALPHA, luego la tecla APPS.

$higo 1.2.5b.png$

Los resultados de estas pulsaciones se muestran en la primera imagen de la Figura$\PageIndex{4}$.

Ahora necesitamos ingresar la expresión |a|−| b|. La función de valor absoluto se encuentra en el menú MATH. Cuando presione la tecla MATH, notará los submenús MATH, NUM, CPX y PRB en la fila superior del menú MATH. Utilice la tecla de flecha derecha para seleccionar el submenú NUM (vea la segunda imagen en la Figura$\PageIndex{4}$). Tenga en cuenta que abs (es la primera entrada en este menú. Esta es la función de valor absoluto necesaria para este ejemplo. Ingrese la expresión$\operatorname{abs}(\mathrm{A})-\operatorname{abs}(\mathrm{B})$ tal y como se muestra en la tercera imagen de la Figura$\PageIndex{4}$. Use la tecla ALPHA como se describió anteriormente para ingresar las variables A y B y cerrar los paréntesis usando la tecla de paréntesis derecha del teclado. Presiona la tecla ENTRAR para evaluar tu expresión.

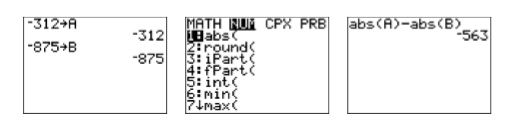
$higo 1.2.4.png$

Figura$\PageIndex{4}$: Evaluar$|a|-|b|$ en$a=-312$ y$b=-875$.

Por lo tanto,$|a|-|b|=-563$.

Ejercicio$\PageIndex{12}$

Utilice la calculadora gráfica para evaluar$|a-b|$ at $a=-312$ and $b=-875$.

Contestar: $563$

Colaboradores

Template:ContribElemAlgebraArnold