2.1: Resolver ecuaciones - Un paso

Última actualización
Guardar como PDF

Page ID: 111609

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Empecemos con la definición de una ecuación.

Ecuación

Una ecuación es una declaración matemática que equipara dos expresiones algebraicas.

La diferencia clave entre una expresión algebraica y una ecuación es la presencia de un signo an igual. Entonces, por ejemplo,

\[2 x+3, \quad x-(3-2 x), \quad \text { and } \quad 2(y+3)-3(1-y) \nonumber \]

son expresiones algebraicas, mientras

\[2 x+3=0, \quad x-(3-2 x)=4, \quad \text { and } \quad 2(y+3)-3(1-y)=-11 \nonumber \]
son ecuaciones. Tenga en cuenta que cada una de las ecuaciones contiene un signo igual, pero las expresiones algebraicas no.

A continuación tenemos la definición de una solución de una ecuación.

Lo que significa ser una solución de una ecuación

Una solución de una ecuación es un valor numérico que satisface la ecuación. Es decir, cuando la variable en la ecuación es reemplazada por la solución, resulta una declaración verdadera.

Ejemplo$\PageIndex{1}$

Demostrar que$8$ es una solución de la ecuación$x-12 = -4$.

Solución

Sustituir$8$$x$ en la ecuación dada y simplificar.

\[\begin{aligned} x-12&=-4 \quad \color{Red} \text { The given equation. } \\ 8-12&=-4 \quad \color{Red} \text { Substitute } 8 \text { for } x . \\ -4&=-4 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Dado que los lados izquierdo y derecho de la última línea son iguales, esto muestra que cuando$8$ se sustituye$x$ en la ecuación resulta una declaración verdadera. Por lo tanto,$8$ es una solución de la ecuación

Ejercicio$\PageIndex{1}$

Cuál de los números$\{1,2,3,4,5\}$ es una solución de la ecuación$2 y+3=7$.

Responder: $2$

Ecuaciones Equivalentes

Ahora que sabemos identificar una solución de una ecuación, definamos lo que significa cuando decimos que dos ecuaciones son equivalentes.

Ecuaciones Equivalentes

Dos ecuaciones son equivalentes si tienen el mismo conjunto de soluciones.

Ejemplo$\PageIndex{2}$

¿Son las ecuaciones$x-3 = 6$ y$x = 9$ equivalentes?

Solución

El número$9$ es la única solución de la ecuación$x − 3 = 6$. De igual manera,$9$ es la única solución de la ecuación$x = 9$. Por lo tanto$x−3 = 6$ y$x = 9$ tener los mismos conjuntos de soluciones y son equivalentes.

Ejercicio$\PageIndex{2}$

¿Son las ecuaciones$x = 5$ y$x-7 = 10$ equivalentes?

Responder: No

Ejemplo$\PageIndex{3}$

¿Son las ecuaciones$x^2 = 1$ y$x = 1$ equivalentes?

Solución

Por inspección, la ecuación$x^2 = 1$ tiene dos soluciones,$-1$ y$1$.

$(-1)^{2}=1 \quad$y$\quad(1)^{2}=1$

Por otro lado, la ecuación$x = 1$ tiene una única solución, a saber$1$. De ahí que las ecuaciones$x^2 = 1$ y$x = 1$ no tengan los mismos conjuntos de soluciones y no sean equivalentes.

Ejercicio$\PageIndex{3}$

¿Son las ecuaciones$x = 1$ y$x^2 = x$ equivalentes?

Responder: No

Como veremos pronto, las ecuaciones equivalentes juegan un papel importante en la búsqueda de la solución de una ecuación.

Envolver y desenvolver, hacer y deshacer

Supongamos que estás envolviendo un regalo para tu primo. Realiza los siguientes pasos en orden.

Ponte el papel de regalo.
Ponte la cinta.
Ponte el lazo decorativo.

Cuando le damos el regalo envuelto a nuestro primo, él cortésmente desenvuelve el presente, “deshaciendo” cada uno de nuestros tres pasos en orden inverso.

Quítate el lazo decorativo.
Quítate la cinta.
Quítate el papel de regalo.

Este envoltorio y desenvuelto aparentemente frívolos de un regalo contiene algunas ideas matemáticas profundamente poderosas. Considera la expresión matemática$x + 4$. Para evaluar esta expresión a un valor particular de$x$, comenzaríamos con el valor dado de$x$, luego agregaríamos$4$.

Vamos a establecer$x$ igual al número$7$. Si agregamos$4$, llegamos al siguiente resultado:$11$

Ahora bien, ¿cómo “desenvolveríamos” este resultado para volver a nuestro número original? Comenzaríamos con nuestro resultado, es decir$11$, luego restar$4$.

Toma nuestro resultado de arriba,$11$. Si restamos$4$, volvemos a nuestro valor original de$x$:$7$

La discusión anterior nos lleva a dos observaciones sumamente importantes.

Nota

La inversa de la suma es la resta. Si empezamos con un número$x$ y sumamos un número$a$, entonces restando$a$ del resultado nos devolverá al número original$x$. En símbolos,

$x + a - a = x$

Es decir, restar$a$ “deshace” el efecto de sumar$a$ y nos devuelve al número original$x$.
La inversa de la resta es la suma. Si empezamos con un número$x$ y restamos un número$a$, entonces sumando$a$ al resultado nos devolverá al número original$x$. En símbolos,

$x - a + a = x$

Es decir, sumar$a$ “deshace” el efecto de restar$a$ y nos devuelve al número original$x$.

Operaciones que producen ecuaciones equivalentes

En Ejemplo$\PageIndex{1}$, vimos que$x = 8$ era una solución de la ecuación$x-12 = -4$. En efecto, las ecuaciones$x = 8$ y$x-12 = -4$ son ecuaciones equivalentes porque ambas tienen los mismos conjuntos de soluciones.

En el caso de la ecuación$x-12 = -4$, es bastante fácil “adivinar” que la solución es$x = 8$, pero a medida que las ecuaciones se vuelven más complicadas, vamos a querer saber exactamente qué operaciones podemos realizar en la ecuación que no cambiarán el conjunto de soluciones. El objetivo es comenzar con una ecuación como

$x-12 = -4$

luego a través de una serie de pasos que no cambian la solución, llegar a la solución

$x =8$

Con estos pensamientos en mente, hay una serie de operaciones que producirán ecuaciones equivalentes (ecuaciones con el mismo conjunto de soluciones). Los dos primeros que vamos a emplear son sumar o restar la misma cantidad de ambos lados de una ecuación.

Agregar la misma cantidad a ambos lados de una ecuación

Agregar la misma cantidad a ambos lados de una ecuación no cambia el conjunto de soluciones. Es decir, si

$a = b$

luego$c$ sumar a ambos lados de la ecuación produce la ecuación equivalente

$a + c = b + c$

Restar la misma cantidad de ambos lados de una ecuación

Restar la misma cantidad a ambos lados de una ecuación no cambia el conjunto de soluciones. Es decir, si

$a = b$

luego restar c de ambos lados de la ecuación produce la ecuación equivalente

$a-c = b-c$

Veamos un ejemplo donde sumar la misma cantidad a ambos lados de la ecuación produce una ecuación equivalente que es la solución a la ecuación original.

Ejemplo$\PageIndex{4}$

Resolver$x-7 = 12$ para$x$.

Solución

Para deshacer el efecto de restar$7$, sumamos$7$ a ambos lados de la ecuación.

\[\begin{aligned} x-7&=12 \quad \color{Red} \text { Original equation. } \\ x-7+7&=12+7 \quad \color{Red} \text { Adding } 7 \text { to both sides of the equation produces an equivalent equation. } \\ x&=19 \quad \color{Red} \text { On the left, adding } 7 \text { "undoes" the effect of subtracting } 7 \text { and returns } x . \text { On the right, } 12+7=19 \end{aligned} \nonumber \]

Por lo tanto, la solución de la ecuación es$19$.

Comprobar: Para verificar, sustituya la solución por$19$ la ecuación original.

\[\begin{aligned} x-7&=12 \quad \color{Red} \text { Original equation. } \\ 19-7&=12 \quad \color{Red} \text { Substitute } 19 \text { for } x \\ 12&=12 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

El hecho de que la última línea del cheque sea una verdadera declaración garantiza que$19$ es una solución de$x-7 = 12$.

Ejercicio$\PageIndex{4}$

Resolver para$x : x-6=4$.

Responder: $10$

En la solución de Ejemplo$\PageIndex{4}$, utilizamos el concepto de la “inversa”. Si empezamos con$x$, restamos$7$, luego sumamos$7$, nos devuelven al número$x$. En símbolos,$x-7+7=x$. Nos devuelven a x porque “restar$7$” y “sumar$7$” son operaciones inversas entre sí. Es decir, haga lo que sea que uno haga, el otro “deshace”.

A continuación, veamos un ejemplo donde restar la misma cantidad de ambos lados de la ecuación produce una ecuación equivalente que es la solución a la ecuación original.

Ejemplo$\PageIndex{5}$

Resolver$x+\dfrac{2}{3}=\dfrac{1}{2}$ para$x$.

Solución

Para deshacer el efecto de sumar$2/3$, restamos$2/3$ de ambos lados de la ecuación.

\ [\ begin {alineado}
x+\ dfrac {2} {3} &=\ dfrac {1} {2}\ quad\ color {Rojo}\ texto {Ecuación original.}\\
x+\ dfrac {2} {3} -\ dfrac {2} {3} &=\ dfrac {1} {2} -\ dfrac {2} {3} quad\ color {Rojo}\ texto {Restar} 2/3\ texto {de ambos lados produce una ecuación equivalente.} \\
x&=\ dfrac {3} {6} -\ dfrac {4} {6}\ color {Rojo}\ texto {A la izquierda, restando} 2/3\ texto {“deshace” el efecto de agregar} 2/3\ texto {y devuelve} x\ texto {. A la derecha, hacer fracciones equivalentes con un denominador común.} \\
x&=-\ dfrac {1} {6}\ quad\ color {Rojo}\ texto {Restar:}\ dfrac {3} {6} -\ dfrac {4} {6} =-\ dfrac {1} {6}
\ end {alineado}\ nonumber\]

Por lo tanto, la solución de la ecuación es$-1/6$.

Consulta: Vamos a usar la calculadora gráfica TI-84 para verificar esta solución.

Almacene el valor$-1/6$ en la variable$X$ usando las siguientes pulsaciones de teclas. El resultado se muestra en la Figura$\PageIndex{1}$.

$fig 2.1.1a.png$

Ingresa el lado izquierdo de la ecuación original: x +2 /3. Utilice las siguientes pulsaciones de teclas. El resultado se muestra en la Figura 2.1.

fig 2.1.1.png — Figura$\PageIndex{1}$: Comprobando la solución a$x +2/3=1 /2$.

Presiona el botón MATH en tu calculadora (ver Figura$\PageIndex{2}$), luego selecciona 1:Frac y presiona el botón ENTER. Esto convertirá el resultado decimal en una fracción (ver Figura$\PageIndex{2}$).

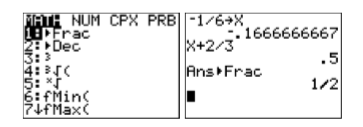
higo 2.1.2.png — Figura$\PageIndex{2}$: Cambiar el resultado a una fracción.

Tenga en cuenta que el resultado está$\dfrac{1}{2},$ demostrando que$-\dfrac{1}{6}$ es una solución de$x+\dfrac{2}{3}=\dfrac{1}{2}$.

Ejercicio$\PageIndex{5}$

Resolver para$x : x+\dfrac{1}{2}=\dfrac{3}{5}$.

Responder: $1/10$

Más operaciones que producen ecuaciones equivalentes

Aquí hay dos operaciones más que producen ecuaciones equivalentes.

Multiplicar ambos lados de una ecuación por una cantidad distinta de cero

Multiplicar ambos lados de una ecuación por una cantidad distinta de cero no cambia el conjunto de soluciones. Es decir, si

$a = b$

y$c \neq 0$, luego multiplicar ambos lados de la ecuación por$c$ produce la ecuación equivalente

$ac = bc$

Dividir ambos lados de una ecuación por una cantidad distinta de cero

Dividir ambos lados de una ecuación por una cantidad distinta de cero no cambia el conjunto de soluciones. Es decir, si

$a = b$

y$c \neq 0$, luego dividir ambos lados de la ecuación por$c$ produce la ecuación equivalente

$\dfrac{a}{c}=\dfrac{b}{c}$

Al igual que la suma y la resta, la multiplicación y la división son operaciones inversas.

Nota

El inverso de la multiplicación es la división. Si empezamos con un número$x$ y multiplicamos por un número$a$, entonces dividir el resultado por el mismo número nos$a$ devuelve al número original$x$. En símbolos,

$\dfrac{a \cdot x}{a}=x$

Es decir, dividiendo por un “deshace” el efecto de multiplicar por$a$ y nos devuelve al número original$x$.

El inverso de la división es la multiplicación. Si empezamos con un número$x$ y dividimos por un número$a$, entonces multiplicar el resultado por el mismo número nos$a$ devuelve al número original$x$. En símbolos,

$a \cdot \dfrac{x}{a}=x$

Es decir, multiplicar por un “deshace” el efecto de dividir por$a$ y nos devuelve al número original$x$.

Veamos un ejemplo donde dividir ambos lados de la ecuación por la misma cantidad produce una ecuación equivalente que es la solución a la ecuación original.

Ejemplo$\PageIndex{6}$

Resolver$-2.1 x=0.42$ para$x$.

Solución

Para deshacer el efecto de multiplicar por$-2.1$, dividimos ambos lados de la ecuación por$-2.1$.

\[\begin{aligned} -2.1 x &=0.42 \quad \color{Red} \text {Original equation.}\\ \frac{-2.1 x}{-2.1} &=\frac{0.42}{-2.1} \quad \color{Red} \text {Dividing both sides by } -2.1 \text{ produces an equivalent equation.}\\ x &=-2 \quad \color{Red} \text {On the left, dividing by } -2.1 \text {"undoes" the effect of multiplying by } -2.1 \text { and returns } x. \text {On the right, divide: } 0.42 /(-2.1)=-2 \end{aligned} \nonumber \]

Por lo tanto, la solución de la ecuación es$-2$.

Comprobar: Para verificar, sustituya la solución por$-2$ la ecuación original.

\[\begin{aligned} -2.1 x&=0.42 \quad \color{Red} \text { Original equation. } \\ -2.1(-2)&=0.42 \quad \color{Red} \text { Substitute }-2 \text { for } x \\ 0.42&=0.42 \quad \color{Red} \text { On the left, multiply: }-2.1(-2)=0.42 \end{aligned} \nonumber \]

El hecho de que la última línea del cheque sea una verdadera declaración garantiza que$-2$ es una solución de$-2.1x =0.42$.

Ejercicio$\PageIndex{6}$

Resolver para$x : -3.6 x = 0.072$.

Responder: $-0.02$

A continuación, veamos un ejemplo donde multiplicar ambos lados de la ecuación por la misma cantidad produce una ecuación equivalente que es la solución a la ecuación original.

Ejemplo$\PageIndex{7}$

Resolver$\dfrac{x}{5}=-10$ para$x$.

Solución

Para deshacer el efecto de dividir por$5$, multiplicamos ambos lados de la ecuación por$5$.

\[\begin{aligned} \dfrac{x}{5} &=-10 \quad \color{Red} \text {Original equation.} \\ 5\left[\dfrac{x}{5}\right] &=[-10] 5 \quad \color{Red} \text {Multiplying both sides by } 5 \text {produces an equivalent equation.} \\ x &=-50 \quad \color{Red} \text {On the left, multiplying by } 5 \text { "undoes" the effect of dividing by } 5 \text { and returns } x \text {. On the right, multiply: } [-10 ] 5=-50 \end{aligned} \nonumber \]

Por lo tanto, la solución de la ecuación es$-50$.

Consulta: Vamos a usar la calculadora gráfica TI-84 para verificar esta solución.

Almacene el valor$-50$ en la variable$X$ usando las siguientes pulsaciones de teclas. El resultado se muestra en la Figura$\PageIndex{3}$.

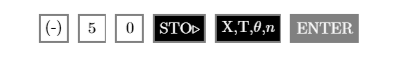
$fig 2.1.3a.png$

Ingrese el lado izquierdo de la ecuación original:$\frac{x}{5}$. Utilice las siguientes pulsaciones de teclas.

higo 2.1.3.png — Figura$\PageIndex{3}$: Comprobando la solución a$x/5=-10$.

Tenga en cuenta que el resultado es$-10$, mostrando que$-50$ es una solución de$x/5=-10$.

Ejercicio$\PageIndex{7}$

Resolver para$x: \dfrac{x}{7}=-2$.

Responder: $-14$

Redacción Matemáticas

Al resolver ecuaciones, observe las siguientes reglas al presentar su trabajo.

Una ecuación por línea. Esto significa que no debes organizar tu trabajo horizontalmente de la siguiente manera:\[x+3=7 \quad x+3-3=7-3 \quad x=4 \nonumber \] Eso son tres ecuaciones en una línea. En su lugar, trabaje verticalmente, escribiendo una ecuación por línea. En la siguiente presentación, anote cómo alineamos los signos iguales en una columna. \[\begin{aligned} x+3 &=7 \\ x+3-3 &=7-3 \\ x &=4 \end{aligned} \nonumber \]
Sumar y restar en línea. No agregue$7$ a ambos lados de la ecuación de la siguiente manera:\[\begin{array}{r}{x-7=12} \\ {+7\;\;\;+7} \\ \hline x=19\end{array} \nonumber \] En su lugar, agregue$7$ “inline” a ambos lados de la ecuación de la siguiente manera:\[\begin{aligned} x-7 &=12 \\ x-7+7 &=12+7 \\ x &=19 \end{aligned} \nonumber \]