2.2: Resolver ecuaciones - Múltiples pasos

Última actualización
Guardar como PDF

Page ID: 111588

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Recordemos la discusión “Envolver” y “Desenvolver” de la Sección 2.1. Para envolver un regalo ponemos el papel de regalo, ponemos la cinta adhesiva y ponemos el lazo decorativo. Para desenvolver el regalo, debemos “deshacer” cada uno de estos pasos en orden inverso. De ahí que para desenvolver el regalo tomamos el lazo decorativo, cogimos la cinta adhesiva, y tomamos el papel de regalo.

Ahora, imagina una máquina que multiplica su entrada por$3$, luego se suma$5$ al resultado. Esta máquina se muestra a la izquierda en la Figura$\PageIndex{1}$.

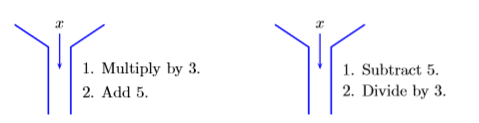
$fig 2.2.1.png$

Figura$\PageIndex{1}$: La segunda máquina “desenvuelve” la primera máquina.

Para “desenvolver” el efecto de la máquina de la izquierda, necesitamos una máquina que “deshaga” cada uno de los pasos de la primera máquina, pero en orden inverso. La máquina “desenvolvidora” se muestra a la derecha en la Figura$\PageIndex{1}$. Primero restará$5$ de su entrada, luego dividirá el resultado por$3$. Obsérvese que cada una de estas operaciones “deshace” la operación correspondiente de la primera máquina, pero en orden inverso.

El siguiente argumento muestra que la segunda máquina “deshace” el funcionamiento de la primera máquina.

Suelte el entero$4$ en la máquina de la izquierda en la Figura$\PageIndex{1}$. Esta máquina primero se multiplicará$4$ por$3$, luego se sumará$5$ al resultado. El resultado es$3(4) + 5$, o$17$.
Para “desenvolver” este resultado,$17$ caiga en la máquina de la derecha. Esta máquina primero resta$5$, luego divide el resultado por$3$. El resultado es$(17-5)/3$, o$4$, el entero original que se puso en la primera máquina.

Ejemplo$\PageIndex{1}$

Resolver para$x : 3 x+5=14$.

Solución

A la izquierda, el orden de operaciones exige que primero multipliquemos$x$ por$3$, luego sumemos$5$. Para resolver esta ecuación$x$, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, primero restaremos de ambos lados$5$ de la ecuación, luego dividiremos ambos lados por$3$.

\[\begin{aligned} 3x+5 &=14 \quad \color{Red} \text{ Original equation. } \\ 3x+5-5 &=14-5 \quad \color{Red} \text{ To "undo" adding 5, subtract 5 from both sides of the equation. } \\ 3x &=9 \quad \color{Red} \text{ Simplify both sides. } \\ \dfrac{3 x}{3} &=\dfrac{9}{3} \quad \color{Red} \text{ To "undo" multiplying by 3, divide both sides of the equation by 3. } \\ x&=3 \quad \color{Red} \text{ Simplify both sides. } \end{aligned} \nonumber \]

Comprobar: Para verificar la solución, sustituya$3$$x$ en la ecuación original y simplificar.

\[\begin{aligned} 3x+5 &=14 \quad \color{Red} \text{ Original equation. } \\ 3(3)+5 &=14 \quad \color{Red} \text{ Substitute 3 for x. } \\ 9+5 &=14 \quad \color{Red} \text{Multiply first: 3(3) = 9. } \\ 14 &=14 \quad \color{Red} \text{ Add: 9 + 5 = 14. } \end{aligned} \nonumber \]

Debido a que la última línea del cheque es una afirmación verdadera, esto garantiza que$3$ es una solución de la ecuación original.

Ejercicio$\PageIndex{1}$

Resolver para$x :2 x+3=7$.

Contestar: $x=2$

Probemos una ecuación con fracciones.

Ejemplo$\PageIndex{2}$

Resolver para$x : \dfrac{x}{5}-\dfrac{2}{3}=\dfrac{1}{2}$.

Solución

A la izquierda, el orden de operaciones exige que primero dividamos$x$ por$5$, luego restemos$2/3$. Para resolver esta ecuación$x$, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, primero sumaremos$2/3$ a ambos lados de la ecuación, luego multiplicaremos ambos lados de la ecuación resultante por$5$.

\[\begin{aligned} \dfrac{x}{5}-\dfrac{2}{3} &=\dfrac{1}{2} \quad \color{Red} \text{ Original equation. }\\ \dfrac{x}{5}-\dfrac{2}{3}+\dfrac{2}{3} &=\dfrac{1}{2}+\dfrac{2}{3} \quad \color{Red} \text{ To "undo" subtracting 2/3, add 2/3 to both sides of the equation. } \end{aligned} \nonumber \]

A la izquierda, simplificamos. A la derecha, hacemos fracciones equivalentes con un denominador común.

\[\begin{aligned} \dfrac{x}{5}&=\dfrac{3}{6}+\dfrac{4}{6} \quad \color{Red} \text { Make equivalent fractions } \\ \dfrac{x}{5}&=\dfrac{7}{6} \quad \color{Red} \text { Add: } \dfrac{3}{6}+\dfrac{4}{6}=\dfrac{7}{6} \end{aligned} \nonumber \]

Ahora “deshacemos” dividiendo por cinco multiplicando ambos lados de la ecuación por$5$.

\[\begin{aligned} \left(\dfrac{x}{5}\right)&=5\left(\dfrac{7}{6}\right) \quad \color{Red} \text { Multiply both sides by } 5 \\ x&=\dfrac{35}{6} \quad \color{Red} \text { On the left, simplify. On the right, multiply: } 5\left(\dfrac{7}{6}\right)=\dfrac{35}{6} \end{aligned} \nonumber \]

Comprobar: Vamos a usar el TI-84 para comprobar esta solución.

Almacene el valor$35/6$ en la variable$X$ usando las siguientes pulsaciones de teclas.

$fig 2.2.2a.png$

El resultado se muestra en la Figura$\PageIndex{2}$.

Ingrese el lado izquierdo de la ecuación original:$x/5 - 2/3$. Utilice las siguientes pulsaciones de teclas.

$fig 2.2.2b.png$

El resultado se muestra en la Figura$\PageIndex{2}$.

$higo 2.2.2.png$

Figura$\PageIndex{2}$: Comprobando la solución a x/5−2/3=1/2.

Presiona el botón MATH en tu calculadora (ver Figura$\PageIndex{3}$), luego selecciona 1: ►Frac, luego presiona el botón ENTER. Esto convertirá el resultado decimal en una fracción (ver Figura$\PageIndex{3}$).

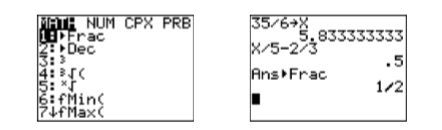
$higo 2.2.3.png$

Figura$\PageIndex{3}$: Cambiar el resultado a una fracción.

Tenga en cuenta que el resultado está$\dfrac{1}{2},$ demostrando que$\dfrac{35}{6}$ es una solución de$\dfrac{x}{5}-\dfrac{2}{3}=\dfrac{1}{2}$.

Ejercicio$\PageIndex{2}$

Resolver para$x: \dfrac{x}{2}-\dfrac{3}{5}=\dfrac{1}{4}$.

Responder: $x = 17/10$

Probemos una ecuación con decimales.

Ejemplo$\PageIndex{3}$

Resolver para$x : 5.2 x+2.3=-3.94$.

Solución

A la izquierda, el orden de las operaciones exige que primero multipliquemos$x$ por$5.2$, luego sumemos 2.3. Para resolver esta ecuación$x$, debemos “deshacer” cada una de estas operaciones en orden inverso. Así, primero restaremos de ambos lados$2.3$ de la ecuación, luego dividiremos ambos lados por$5.2$.

\[\begin{aligned} 5.2 x+2.3 &=-3.94 \quad \color{Red} \text{ Original equation. }\\ 5.2 x+2.3-2.3 &=-3.94-2.3 \quad \color{Red} \text{ To "undo" adding 2.3, subtract 2.3 from both sides.}\\ 5.2 x &=-6.24 \quad \color{Red} \text{ On the left, simplify. On the right, add: -3.94-2.3=-6.24. }\\ \frac{5.2 x}{5.2} &=\frac{-6.24}{5.2} \quad \color{Red} \text{ To undo multiplying by 5.2, divide both sides by 5.2. }\\ x &=-1.2 \quad \color{Red} \text{ On the left, simplify. On the right, divide: -6.24/5.2=-1.2. } \end{aligned} \nonumber \]

Comprobar: Para verificar la solución, sustituya$-1.2$$x$ en la ecuación original y simplificar.

\[\begin{aligned} 5.2 x+2.3 &=-3.94 \quad \color{Red} \text{ Original equation. }\\ 5.2(-1.2)+2.3 &=-3.94 \quad \color{Red} \text{ Substitute -1.2 for x. }\\ -6.24+2.3 &=-3.94 \quad \color{Red} \text{ Multiply: 5.2(-1.2)=-6.24 }\\ -3.94 &=-3.94 \quad \color{Red} \text{ Add: -6.24+2.3=-3.94 } \end{aligned} \nonumber \]

Debido a que la última línea del cheque es una afirmación verdadera, esto garantiza que$-1.2$ es una solución de la ecuación original.

Ejercicio$\PageIndex{3}$

Resolver para$x: 3.25-1.2 x=0.37$.

Contestar: $x=2.4$

Variables en ambos lados de la ecuación

No es raro que la variable para la que estás resolviendo aparezca en términos a ambos lados de la ecuación. Consideremos, por ejemplo, la ecuación$2x+3=5−7x$. En casos como este, es útil tener una comprensión general de lo que significa “resolver”$x$.

Resolver para x

Cuando se le pide que resuelva una ecuación para$x$, el objetivo es manipular la ecuación en la forma final

$x=\text{"Stuff"}$

donde “Stude” es una expresión matemática válida que puede contener otras variables, símbolos matemáticos, etc., pero no debe contener ninguna ocurrencia de la variable$x$.

En esta sección, “Stude” siempre será un solo número, pero en la Sección 2.4, Fórmulas, “Stu,” asumirá complejidad añadida, incluyendo variables distintas a$x$.

Estrategia para resolver$x$

Cuando se le pide que resuelva una ecuación para$x$, una estrategia común es aislar todos los términos que contienen la variable$x$ en un lado de la ecuación y mover todos los términos que no contienen la variable$x$ al otro lado de la ecuación.

Ejemplo$\PageIndex{4}$

Resolver$3-2 x=5 x+9$ para$x$.

Solución

Necesitamos aislar todos los términos que contengan$x$ en un lado de la ecuación. Podemos eliminar$5x$ del lado derecho de$3−2x =5x+9$ restando$5x$ de ambos lados de la ecuación.

\[\begin{aligned} 3-2x &=5x+9 \quad \color{Red} \text { Original equation. } \\ 3-2x-5x & =5x+9-5x \quad \color{Red} \text { Subtract } 5x \text { from both sides. } \\ 3-7x &=9 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

A continuación, elimine$3$ del lado izquierdo de la última ecuación restando$3$ de ambos lados de la ecuación.

\[\begin{aligned} 3-7x-3 & =9-3 \quad \color{Red} \text { Subtract } 3 \text { from both sides. } \\ -7x & =6 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Observe cómo hemos aislado todos los términos que contienen$x$ en un lado de la ecuación.

\[\begin{aligned} \dfrac{-7 x}{-7}&=\dfrac{6}{-7} \quad \color{Red} \text { Divide both sides by }-7 \\ x&=-\dfrac{6}{7} \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Comprobar: Para verificar la solución, sustituya$-6/7$$x$ en la ecuación original.

\ [\ begin {alineado}
3-2 x &=5 x+9\ quad\ color {Rojo}\ texto {Ecuación original.}\\
3-2\ izquierda (-\ dfrac {6} {7}\ derecha) &=5\ izquierda (-\ dfrac {6} {7}\ derecha) +9\ quad\ color {Rojo}\ texto {Sustituir -6/7 por x.}\
3+\ dfrac {12} {7} &=-\ dfrac {30} {7} +9\ quad\ color {Rojo}\ texto { Multiplicar:} -2 (-6/7) =12/7\ texto {y} 5 (-6/7) =-30/7. \\
\ dfrac {21} {7} +\ dfrac {12} {7} &=-\ dfrac {30} {7} +\ dfrac {63} {7}\ quad\ color {Rojo}\ text {Hacer fracciones equivalentes con un denominador común.}\
\ dfrac {33} {7} &=\ dfrac {33} {7}\ quad\ {Rojo}\ texto {Agregar.}
\ final {alineado}\ nonumber\]

Debido a que la última línea del cheque es una afirmación verdadera, esto garantiza que$-6/7$ es una solución de la ecuación original.

Ejercicio$\PageIndex{4}$

Resolver para$x: 4x+7=5-8x$.

Contestar: $x=-1 / 6$

Simplificar expresiones al resolver ecuaciones

A veces necesitamos simplificar las expresiones antes de poder aislar los términos que contienen$x$.

Ejemplo$\PageIndex{5}$

Resolver para$x: 2(3 x+1)-3(4-2 x)=-34$.

Solución

Primero simplificaremos la expresión en el lado izquierdo de la ecuación usando el Orden de Operaciones Rules Guiding.

\[\begin{aligned}2(3 x+1)-3(4-2 x)&=-34 \quad \color{Red} \text { Original equation. } \\ 6x+2-12+6x&=-34 \quad \color{Red} \text { Multiply: } 2(3 x+1)=6 x+2 \text {, Multiply: } -3(4-2 x)=-12+6 x\\ 12 x-10&=-34 \quad \color{Red} \text { Add: } 6x+6 x=12x \text {, Add: } 2-12=-10\\ \end{aligned} \nonumber \]

Para “deshacer” restar$10$, sumamos$10$ a ambos lados de la ecuación.

\[\begin{aligned} 12x-10+10&=-34+10 \quad \color{Red} \text { Add } 10 \text { to both sides. } \\ 12x&=-24 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Para “deshacer” multiplicando por$12$, dividimos ambas partes por$12$.

\[\begin{aligned} \dfrac{12 x}{12}&=\dfrac{-24}{12} \quad \color{Red} \text { Divide both sides by } 12\\ x&=-2 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Comprobar: Vamos a usar el TI-84 para comprobar esta solución.

Primero, almacene −2 en la variableX usando las siguientes pulsaciones de teclas.

$fig 2.2.4a.png$

El resultado se muestra en la primera imagen de la Figura$\PageIndex{4}$.

Ingrese el lado izquierdo de la ecuación original:$2(3x + 1)-3(4-2x)$. Utilice las siguientes pulsaciones de teclas.

$fig 2.2.4b.png$

El resultado se muestra en la segunda imagen de la Figura$\PageIndex{4}$.

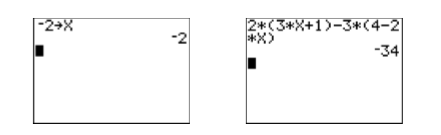
$higo 2.2.4.png$

Figura$\PageIndex{4}$: Comprobando la solución a$2(3x + 1)-3(4-2x)=-34$.

Tenga en cuenta que cuando$-2$ se sustituye$x$ en la izquierda de la ecuación, el resultado es$-34$, igualando el lado derecho de la ecuación. Así, la solución$-2$ comprueba.

Ejercicio$\PageIndex{5}$

Resolver para$x : 2 x-(x-2)=2(x+7)$.

Contestar: $x=-12$

Ejemplo$\PageIndex{6}$

Resolver para$x : 2 x-5(3-2 x)=4(x-1)$.

Solución

Primero simplificaremos las expresiones en cada lado de la ecuación usando el Orden de Operaciones Rules Guiding.

\[\begin{aligned} 2x-5(3-2x)&=4(x-1) \quad \color{Red} \text { Original equation. } \\ 2x-15+10x&=4x-4 \quad \color{Red} \text { On the left, distribute the -5. On the right, distribute the 4.} \\ 12x-15&=4x-4 \quad \color{Red} \text { On the left, add: } 2x+10x=12 x \end{aligned} \nonumber \]

A continuación, necesitamos aislar términos que contengan la variable$x$ en un lado de la ecuación. Para eliminar el término$4x$ del lado derecho, restamos$4x$ de ambos lados de la ecuación.

\[\begin{aligned} 12x-15-4x&=4x-4-4x \quad \color{Red} \text { Subtract } 4 x \text { from both sides. } \\ 8x-15&=-4 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Para eliminar el término$-15$ del lado izquierdo, agregamos$15$ a ambos lados de la ecuación.

\[\begin{aligned} 8x-15+15&=-4+15 \quad \color{Red} \text { Add } 15 \text { to both sides. } \\ 8x&=11 \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Por último, para “deshacer” multiplicando por$8$, dividimos ambas partes por$8$.

\[\begin{aligned} \dfrac{8x}{8}&=\dfrac{11}{8} \quad \color{Red} \text { Divide both sides by } 8 \\ x&=\dfrac{11}{8} \quad \color{Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Comprobar: Vamos a usar el TI-84 para comprobar esta solución.

Primero, almacene 11/8 en la variable X usando las siguientes pulsaciones de teclas.

$fig 2.2.5a.png$

El resultado se muestra en la primera imagen de la Figura$\PageIndex{5}$.

Ingrese el lado izquierdo de la ecuación original:$2x-5(3-2x)$. Utilice las siguientes pulsaciones de teclas.

$higo 2.2.5b.png$

El resultado se muestra en la segunda imagen de la Figura$\PageIndex{5}$.

Ingrese el lado derecho de la ecuación original:$4(x - 1)$. Utilice las siguientes pulsaciones de teclas.

$fig 2.2.5c.png$

El resultado se muestra en la tercera imagen de la Figura$\PageIndex{5}$.

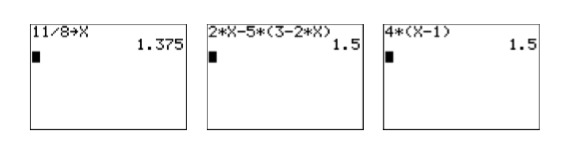
$higo 2.2.5.png$

Figura$\PageIndex{5}$: Comprobando la solución a$2x-5(3-2x) = 4(x-1)$.

No hay necesidad de usar el 1: ►Frac del menú MATH esta vez. El hecho de que ambos lados de la ecuación evalúen a un idéntico$1.5$ cuando$x = 11 /8$ garantiza que$11/8$ es una solución de$2x-5(3-2x) = 4(x-1)$.

Ejercicio$\PageIndex{6}$

Resolver para$x:5(1-x)=2(x+3)-(x-1)$.

Contestar: $x=-1 / 3$

Colaboradores

Template:ContribElemAlgebraArnold