6.3: Factorización ax² + bx + c cuando a =1

Última actualización
Guardar como PDF

Page ID: 111674

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección nos concentramos en aprender a factorizar trinomios teniendo la forma$ax^2 +bx+c$ cuando$a = 1$. La primera tarea es asegurarse de que todos puedan identificar adecuadamente a los coecients$a$,$b$, y$c$.

Ejemplo$\PageIndex{1}$

Comparar$x^2−8x−9$ con la forma$ax^2 +bx+c$ e identificar a los coefcientes$a$,$b$, y$c$.

Solución

Alinee el trinomio$x^2−8x−9$ con la forma estándar$ax^2 +bx+c$, luego compare los coecients. Obsérvese que el coecient entendido de$x^2$ es$1$.

\[\begin{array}{l}{a x^{2}+b x+c} \\ {{\color {Red}1} x^{2}-8 x-9}\end{array} \nonumber \]

Vemos eso$a = 1$,$b = −8$, y$c = −9$. Debido a que lo es el principal principal$1$, este es el tipo de trinomio que aprenderemos a factorizar en esta sección.

Ejercicio$\PageIndex{1}$

Comparar$2x^2 +5x−3$ con la forma$ax^2 + bx + c$ e identificar a los coefcientes$a$,$b$, y$c$.

Responder: $a = 2$,$b = 5$,$c =−3$

Ejemplo$\PageIndex{2}$

Comparar$−40 + 6x^2 − x$ con la forma$ax^2 + bx + c$ e identificar a los coefcientes$a$,$b$, y$c$.

Solución

Primero,$−40+ 6x^2 −x$ organízalo en potencias descendentes de$x$, luego alinearlo con la forma estándar$ax^2 +bx+c$ y compare coecients. Obsérvese que el coecient entendido de$x$ es$−1$.

\[\begin{array}{l}{a x^{2}+b x+c} \\ {6 x^{2}-{\color {Red} 1} x-40}\end{array} \nonumber \]

Vemos eso$a = 6$,$b = −1$, y$c = −40$. Debido a que lo es el principal principal$6$, tendremos que esperar hasta que aprendamos a factorizar$ax^2 + bx + c$ cuando$a \neq 1$ en la sección 6.4 antes de aprender a factorizar este trinomio.

Ejercicio$\PageIndex{2}$

Comparar$3x +9−7x^2$ con la forma$ax^2 + bx + c$ e identificar a los coefcientes$a$,$b$, y$c$.

Responder: $a = −7$,$b = 3$,$c =9$

En esta sección, el coeciente principal debe igualar$1$. Nuestro trabajo en esta sección se centrará únicamente en trinomios de la forma$x^2 + bx + c$, es decir, la forma$ax^2 + bx + c$ donde$a = 1$.

El$ac$ -Método

Ahora vamos a introducir una técnica llamada$ac$ -método (o$ac$ -test) para factorizar trinomios de la forma$ax^2 +bx+c$ cuando$a = 1$. En la próxima sección 6.4 sobre factorización$ax^2 + bx + c$ cuándo$a \neq 1$, veremos que este método también se puede emplear cuando$a \neq 1$, con una excepción menor. Pero para lo que resta de esta sección, nos enfocamos estrictamente en trinomios cuyo principal coeciente es$1$.

Comencemos por encontrar el siguiente producto:

\[\begin{aligned}(x+12)(x-4) &=x(x-4)+12(x-4) \quad \color {Red} \text { Apply the distributive property. } \\ &=x^{2}-4 x+12 x-48 \quad \color {Red } \text { Distribute again. } \\ &=x^{2}+8 x-48 \quad \color {Red} \text { Simplify. }\end{aligned} \nonumber \]

Ahora bien, ¿podemos revertir el proceso? Es decir, ¿podemos comenzar$x^2 +8x−48$ y colocarlo en su forma factorizada original$(x + 12)(x−4)$? La respuesta es sí, si aplicamos el siguiente procedimiento.

El$ac$-method

Comparar el polinomio dado con la forma estándar$ax^2 + bx + c$, determinar los coecients$a$, y$b$$c$, luego proceder de la siguiente manera:

Multiplique los coecientes$a$$c$ y determinen su producto$ac$. Enumere todos los pares enteros cuyo producto es igual$ac$.
Encierra en círculo el par en la lista producida en el paso 1 cuya suma es igual$b$, el coefíciente del término medio de$ax^2 + bx + c$.
Reemplace el término medio$bx$ con una suma de términos similares usando el par con un círculo del paso 2.
Factor por agrupación.
Comprueba el resultado usando el atajo FOIL.

Sigamos los pasos del$ac$ -método a factorizar$x^2 +8x−48$.

Ejemplo$\PageIndex{3}$

Factor:$x^2 +8x−48$.

Solución

Comparar$x^2+8x−48$$ax^2+bx+c$ e identificar$a = 1$,$b = 8$, y$c = −48$. Tenga en cuenta que el principal coecient es$a = 1$. Calcular$ac$. Tenga en cuenta que$ac = (1)(−48)$, entonces$ac =−48$. Listar todos los pares enteros cuyo producto es$ac = −48$.

\[\begin{array}{ll}{1,-48} & {-1,48} \\ {2,-24} & {-2,24} \\ {3,-16} & {-3,16} \\ {4,-12} & { -4,12} \\ {6,-8} & {-6,8}\end{array} \nonumber \]

Encierra en círculo el par ordenado cuya suma es$b = 8$.

\[\begin{array}{ll}{1,-48} & {-1,48} \\ {2,-24} & {-2,24} \\ {3,-16} & {-3,16} \\ {4,-12} & {\color {Red}-4,12} \\ {6,-8} & {-6,8}\end{array} \nonumber \]

Reemplace el término medio$8x$ con una suma de términos similares usando el par circular cuya suma es$8$.

\[x^2{\color {Red}+8x}-48 = x^2{\color {Red}-4x + 12x}-48 \nonumber \]

Factor por agrupación.

\[\begin{aligned} x^{2}+8 x-48 &=x(x-4)+12(x-4) \\ &=(x+12)(x-4) \end{aligned} \nonumber \]

Usa el atajo FOIL para verificar mentalmente tu respuesta. Para determinar el producto$(x + 12)(x−4)$, siga estos pasos:

Multiplicar los términos en las posiciones “Primera”:$x^2$.
Multiplicar los términos en las posiciones “Exterior” e “Interior” y combinar los resultados mentalmente:$−4x + 12x =8x$.
Multiplicar los términos en las “Últimas” posiciones:$−48$.

Es decir:

\[(x+12)(x-4) = \begin{array}{ccccccc} {\color {Red}F} & & {\color {Red}O} & & {\color {Red}I} & & {\color {Red}L}\\ x^2&-&4x&+&12x&-&48 \end{array} \nonumber \]

Combinando términos similares,$(x + 12)(x−4) = x^2 +8x−48$, que es el trinomio original, así que nuestra solución comprueba. Tenga en cuenta que si combina los productos “Exterior” e “Interior” mentalmente, el cheque va aún más rápido.

Ejercicio$\PageIndex{3}$

Factor:$x^2 + 11x + 28$

Contestar: $(x+4)(x+7)$

Algunos lectores podrían preguntar “¿Es una coincidencia que la pareja encerrada en un círculo$\color {Red} −4,12$ pareciera 'caer en su lugar' en la factorización resultante$(x+12)(x−4)$?” Antes de responder a esa pregunta, probemos con otro ejemplo.

Ejemplo$\PageIndex{4}$

Factor:$x^2 −9x−36$.

Solución

Compare$x^2−9x−36$ con$ax^2+bx+c$ y tenga en cuenta que$a = 1$,$b = −9$, y$c =−36$. Calcular$ac = (1)(−36)$, entonces$ac = −36$.

En este punto, algunos lectores podrían preguntar “¿Y si empiezo a enumerar los pares ordenados y veo el par que necesito? ¿Necesito seguir publicando los pares restantes?

La respuesta es “No”. En este caso, comenzamos a enumerar los pares enteros cuyo producto es$ac = −36$, pero somos conscientes de que necesitamos un par entero cuya suma sea$b =−9$. El par entero$3$ y$−12$ tiene un producto que iguala$ac =−36$ y una suma igual$b =−9$.

\[\begin{array}{r}{1,-36} \\ {2,-18} \\ {\color {Red}3,-12} \end{array} \nonumber \]

Tenga en cuenta cómo dejamos de enumerar pares ordenados en el momento en que encontramos el par que necesitábamos. A continuación, reemplace el término medio$−9x$ con una suma de términos similares usando el par con un círculo.

\[x^2{\color {Red}-9x}-36 = x^2{\color {Red}+3x-12x}-36 \nonumber \]

Factor por agrupación.

\[\begin{aligned} x^{2}{\color {Red}-9 x}-36 &=x(x+3)-12(x+3) \\ &=(x-12)(x+3) \end{aligned} \nonumber \]

Usa el atajo FOIL para verificar tu respuesta.

\[(x+3)(x-12) = \begin{array}{ccccccc} {\color {Red}F} & & {\color {Red}O} & & {\color {Red}I} & & {\color {Red}L}\\ x^2&-&12x&+&3x&-&36 \end{array} \nonumber\]

Combinando términos similares$(x + 3)(x−12) = x^2 −9x−36$,, el trinomio original. Nuestras comprobaciones de soluciones.

Ejercicio$\PageIndex{4}$

Factor:$x2 + 10x−24$.

Contestar: $( x + 12)(x−2)$

Acelerar un poco las cosas

Los lectores podrían volver a preguntar “¿Es una coincidencia que la pareja encerrada en un círculo$\color {Red} 3,−12$ pareciera 'caer en su lugar' en la factorización resultante$(x−12)(x + 3)$?” La respuesta es “No”, no es una coincidencia. Siempre que el principal coeciente del trinomio$ax^2 +bx+c$ sea$a = 1$, siempre se puede “colocar en su lugar” el par en círculo para llegar a la factorización final, omitiendo el factoring por agrupación.

Algunos lectores también podrían estar preguntando “¿De verdad tengo que enumerar alguno de esos pares ordenados si ya reconozco el par que necesito?” La respuesta es “¡No!” Si ves el par que necesitas, déjalo caer en su lugar.

Ejemplo$\PageIndex{5}$

Factor:$x^2 −5x−24$.

Solución

Compare$x^2−5x−24$ con$ax^2+bx+c$ y tenga en cuenta que$a = 1$,$b =−5$, y$c =−24$. Calcular$ac = (1)(−24)$, entonces$ac = −24$. Ahora, ¿se te ocurre un par entero cuyo producto es$ac = −24$ y cuya suma es$b = −5$? Para algunos, el par requerido simplemente se les entra en la cabeza:$−8$ y$3$. El producto de estos dos enteros es$−24$ y su suma es$−5$. “Deja caer” este par en su lugar y ya está.

\[x^2 −5x−24 = (x−8)(x + 3) \nonumber \]

Usa el atajo FOIL para verificar tu respuesta.

\[(x-8)(x+3) = \begin{array}{ccccccc} {\color {Red}F} & & {\color {Red}O} & & {\color {Red}I} & & {\color {Red}L}\\ x^2&+&3x&-&8x&-&24 \end{array} \nonumber\]

Combinando términos similares$(x−8)(x + 3) =x^2 −5x−24$,, el trinomio original. Nuestras comprobaciones de soluciones.

Ejercicio$\PageIndex{5}$

Factor:$x^2 −12x + 35$

Contestar: $(x−7)(x−5)$

La técnica “Drop in Place” de Ejemplo nos$\PageIndex{5}$ permite revisar un poco el$ac$ método.

Revisado$ac$-method

Comparar el polinomio dado con la forma estándar$ax^2 + bx + c$, determinar los coecients$a$, y$b$$c$, luego determinar un par de enteros cuyo producto es igual$ac$ y cuya suma es igual$b$. Entonces tienes dos opciones:

Escribe el término medio como un producto de términos similares usando el par ordenado cuyo producto es$ac$ y cuya suma es$b$. Completar el proceso de factorización factorizando por agrupación.
(Sólo funciona si$a =1$.) Simplemente “coloque en su lugar” el par ordenado cuyo producto es$ac$ y cuya suma es$b$ completar el proceso de factorización. Nota: Aprenderemos sobre la factorización$ax^2 + bx + c$ cuando$a \neq 1$ en la sección 6.4 por qué esta opción de “caída en el lugar” no funciona cuando$a \neq 1$

Se recomienda encarecidamente a los lectores que verifiquen su factorización determinando el producto utilizando el método FOIL. Si esto produce el trinomio original, la factorización es correcta.

Ecuaciones no lineales revisitadas

La capacidad de factorizar trinomios de la forma$ax^2 +bx+c$$a = 1$, donde, aumenta el número de ecuaciones no lineales que ahora somos capaces de resolver.

Ejemplo$\PageIndex{6}$

Resuelve la ecuación$x^2 =2 x + 3$ tanto algebraica como gráficamente, luego compara tus respuestas.

Solución

Debido a que hay un poder$x$ mayor que uno, la ecuación es no lineal. Hacer un lado cero.

\[\begin{aligned} x^{2} &=2 x+3 \quad \color {Red} \text { Original equation. } \\ x^{2}-2 x &=3 \quad \color {Red} \text { Subtract } 2 x \text { from both sides. } \\ x^{2}-2 x-3 &=0 \quad \color {Red} \text { Subtract } 3 \text { from both sides. }\end{aligned} \nonumber \]

Compare$x^2−2x−3$ con$ax^2+bx+c$ y tenga en cuenta que$a = 1$,$b =−2$ y$c =−3$. Necesitamos un par entero cuyo producto es$ac = −3$ y cuya suma es$b = −2$. El par entero$1$ y$−3$ viene a la mente. “Dejar caer” estos en su lugar para factorizar.

\[(x + 1)(x-3) = 0 \quad \color {Red} \text {Factor.} \nonumber \]

Tenemos un producto que equivale a cero. Utilice la propiedad cero del producto para completar la solución.

\[\begin{aligned} x+1 &=0 \\ x &=-1 \end{aligned} \nonumber \]

\[\begin{array}{r}{x-3=0} \\ {x=3}\end{array} \nonumber \]

Así, las soluciones de$x^2 =2x + 3$ son$x = −1$ y$x = 3$.

Solución gráfica:

Cargue cada lado de la ecuación$x^2 =2 x + 3$ en el menú Y= de su calculadora gráfica,$y = x^2$ en$\mathbb {Y1}$,$y =2x + 3$ en$\mathbb {Y2}$ (ver Figura$\PageIndex{1}$). Seleccione 6:ZStandard en el menú ZOOM para producir la imagen a la derecha en la Figura$\PageIndex{1}$.

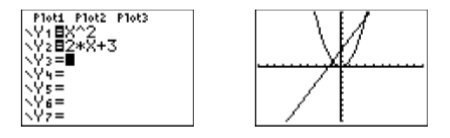
higo 6.3.1.png — Figura$\PageIndex{1}$: Croquis$y = x^2$ y$y =2x + 3$.

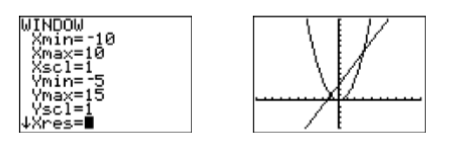
Uno de los puntos de intersección es visible a la izquierda, pero el segundo punto de intersección está muy cerca de la parte superior de la pantalla a la derecha (ver Figura$\PageIndex{1}$). Extendamos un poco la parte superior de la pantalla. Presione el botón VENTANA y realice ajustes a$\mathbb{Ymin}$ y$\mathbb{Ymax}$ (ver Figura$\PageIndex{2}$), luego presione el botón GRAPAR para adoptar los cambios.

Tenga en cuenta que ambos puntos de intersección ahora son visibles en la ventana de visualización (ver Figura$\PageIndex{2}$). Para encontrar las coordenadas de los puntos de intersección, seleccione 5:intersectar en el menú CALC. Presione la tecla ENTRAR para aceptar la “Primera curva”, presione ENTRAR nuevamente para aceptar la “Segunda curva”, luego presione ENTRAR nuevamente para aceptar la posición actual del cursor como su suposición. El resultado se muestra en la imagen de la izquierda en la Figura$\PageIndex{3}$. Repita el proceso para encontrar el segundo punto de intersección, solo cuando llegue el momento de ingresar su “Adivina”, use la tecla de flecha hacia la derecha para mover el cursor más cerca del segundo punto de intersección que el primero.

higo 6.3.2.png — Figura$\PageIndex{2}$: Ajuste de la vista.

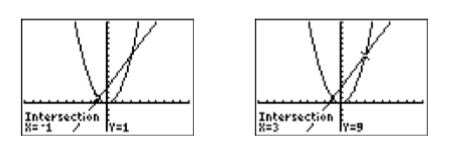
higo 6.3.3.png — Figura$\PageIndex{3}$: Utilice **5:intersectar** del menú **CALC** para encontrar puntos de intersección.

Reportando la solución en tu tarea:

Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

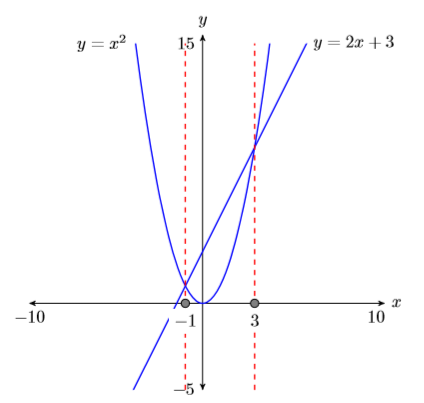
higo 6.3.4.png — Figura$\PageIndex{4}$: Reportando tu solución gráfica en tu tarea.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{4}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{4}$).
Etiquetar cada gráfica con su ecuación (ver Figura$\PageIndex{4}$).
Coloca líneas verticales discontinuas a través de cada punto de intersección. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$x^2 =2 x + 3$ (ver Figura$\PageIndex{4}$).

Finalmente, observe cómo las soluciones gráficas de$x^2 =2 x + 3$, es decir$x = −1$ y$x = 3$, coinciden con las soluciones encontradas utilizando el método algebraico. Esto es evidencia sólida de que ambos métodos de solución son correctos. Sin embargo, no está de más verificar las respuestas finales en la ecuación original, sustituyendo$−1$ por$x$ y$3$ para$x$.

\[\begin{aligned} x^{2} &=2 x+3 \\(-1)^{2} &=2(-1)+3 \\ 1 &=-2+3 \end{aligned} \nonumber \]

\[\begin{aligned} x^{2} &=2 x+3 \\(3)^{2} &=2(3)+3 \\ 9 &=6+3 \end{aligned} \nonumber \]

Porque las dos últimas afirmaciones son afirmaciones verdaderas, las soluciones$x = −1$ y$x = 3$ verifican la ecuación original$x^2 =2x + 3$.

Ejercicio$\PageIndex{6}$

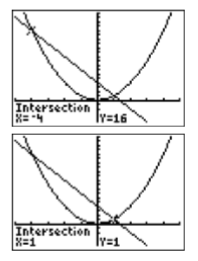
Resuelve la ecuación$x^2 = −3x + 4$ tanto algebraica como gráficamente, luego compara tus respuestas.

Contestar

$-4$,$1$

$Ejercicio 6.3.6.png$

Ejemplo$\PageIndex{7}$

Resuelve la ecuación$x^2 −4x−96 = 0$ tanto algebraica como gráficamente, luego compara tus respuestas.

Solución

Debido a que hay un poder$x$ mayor que uno, la ecuación$x^2 − 4x−96 = 0$ es no lineal. Ya tenemos un lado cero, así podemos proceder con el factoring. Empezar a enumerar pares enteros cuyo producto es$ac = −96$, consciente del hecho de que necesitamos un par cuya suma es$b = −4$.

\[\begin{array}{l}{1,-96} \\ {2,-48} \\ {3,-32} \\ {4,-24} \\ {6,-16} \\ {\color {Red}8,-12} \\ \end{array} \nonumber \]

Tenga en cuenta que paramos el proceso de listado tan pronto como nos encontramos con un par cuya suma era$b = −4$. “Dejar caer” este par en su lugar para factorizar el trinomio.

\[\begin{aligned}x^{2}-4 x-96 &=0 \quad \color {Red} \text { Original equation. } \\ (x+8)(x-12) &=0 \quad \color {Red} \text { Factor. }\end{aligned} \nonumber \]

Tenemos un producto que equivale a cero. Utilice la propiedad cero del producto para completar la solución.

\[\begin{aligned} x+8 &=0 \\ x &=-8 \end{aligned} \nonumber \]

\[\begin{aligned} x-12 &=0 \\ x &=12 \end{aligned} \nonumber \]

Así, las soluciones de$x^2 −4x−96 = 0$ son$x =−8$ y$x = 12$.

Solución gráfica:

Carga la ecuación$y = x^2 −4x−96$$\mathbb{Y1}$ en el menú Y= de tu calculadora gráfica (ver Figura$\PageIndex{5}$). Seleccione 6:ZStandard en el menú ZOOM para producir la imagen a la derecha en la Figura$\PageIndex{5}$.

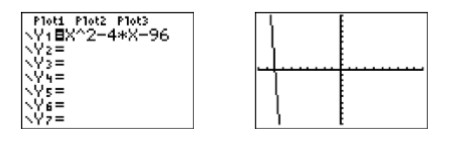
higo 6.3.5.png — Figura$\PageIndex{5}$: Esbozar la gráfica de$y = x^2 −4x−96$.

Cuando el grado de un polinomio es dos, estamos acostumbrados a ver algún tipo de parábola. En Figura$\PageIndex{5}$, vimos que la gráfica bajaba y ola pantalla, pero no la vimos girar y volver a subir. Ajustemos los parámetros WINDOW para que el vértice (punto de inflexión) de la parábola y ambas$x$ -intercepciones sean visibles en la ventana de visualización. Después de cierta experimentación, los ajustes mostrados en la Figura$\PageIndex{6}$ revelan el vértice y las$x$ -intercepciones. Presione el botón GRAPAR para producir la imagen a la derecha en la Figura$\PageIndex{6}$.

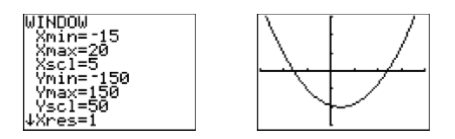
higo 6.3.6.png — Figura$\PageIndex{6}$: Ajuste de la vista.

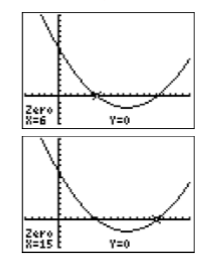
Tenga en cuenta que ambas$x$ intercepciones de la parábola ahora son visibles en la ventana de visualización (ver Figura$\PageIndex{6}$). Para encontrar las coordenadas de las$x$ -intercepciones, seleccione 2:cero en el menú CALC. Use las teclas de flecha izquierda y derecha para mover el cursor hacia la izquierda de la primera$x$ intersección, luego presione ENTRAR para marcar el “Límite izquierdo”. A continuación, mueva el cursor a la derecha de la primera$x$ intersección, luego presione ENTRAR para marcar el “Límite a la derecha”. Presiona ENTRAR para aceptar la posición actual del cursor como tu “Adivina”. El resultado se muestra en la imagen de la izquierda en la Figura$\PageIndex{7}$. Repita el proceso para encontrar las coordenadas de la segunda$x$ intersección. El resultado se muestra en la imagen de la derecha en la Figura$\PageIndex{7}$.

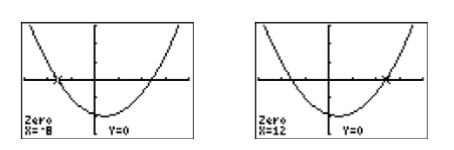
higo 6.3.7.png — Figura$\PageIndex{7}$: Use **2:cero** del menú **CALC** para encontrar las$x$ intercepciones.

Reportando la solución en tu tarea: Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{8}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{8}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{8}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intersección. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$x^2−4x−96 = 0$ (ver Figura$\PageIndex{8}$).

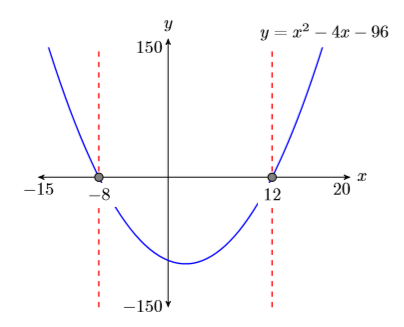
higo 6.3.8.png — Figura$\PageIndex{8}$: Reportando tu solución gráfica en tu tarea.

Finalmente, observe cómo las soluciones gráficas de$x^2 −4x−96 = 0$, es decir$x = −8$ y$x = 12$, coinciden con las soluciones encontradas utilizando el método algebraico. Esto es evidencia sólida de que ambos métodos de solución son correctos. Sin embargo, no está de más verificar las respuestas finales en la ecuación original, sustituyendo$−8$ por$x$ y$12$ para$x$.

\[\begin{array}{r}{x^{2}-4 x-96=0} \\ {(-8)^{2}-4(-8)-96=0} \\ {64+32-96=0}\end{array} \nonumber \]

\[\begin{aligned} x^{2}-4 x-96 &=0 \\(12)^{2}-4(12)-96 &=0 \\ 144-48-96 &=0 \end{aligned} \nonumber \]

Porque las dos últimas afirmaciones son afirmaciones verdaderas, las soluciones$x = −8$ y$x = 12$ verifican la ecuación original$x^2 −4x−96−0$.

Ejercicio$\PageIndex{7}$

Resolver la ecuación$x^2 −21x + 90 = 0$ both algebraically and graphically, then compare your answers.

Contestar

$6$,$15$

$Ejercicio 6.3.7.png$

El\(ac\) -Método

Acelerar un poco las cosas

Ecuaciones no lineales revisitadas