6.2: Resolver ecuaciones no lineales

Última actualización
Guardar como PDF

Page ID: 111673

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Comenzamos introduciendo una propiedad que será utilizada ampliamente en esta y futuras secciones.

La propiedad del producto cero

Si el producto de dos o más números es igual a cero, entonces al menos uno de los números debe ser igual a cero. Es decir, si

$ab =0$

entonces

$a = 0$o$b =0$

Usemos la propiedad cero del producto para resolver algunas ecuaciones.

Ejemplo$\PageIndex{1}$

Resolver para$x$:$(x+3)(x-5)=0$

Solución

El producto de dos factores es igual a cero.

\[(x+3)(x-5)=0 \nonumber \]

De ahí que al menos uno de los factores debe ser igual a cero. Usando la propiedad cero del producto, establezca cada factor igual a cero, luego resuelva las ecuaciones resultantes para$x$.

\[\begin{aligned} x+3 &=0 \\ x &=-3 \end{aligned} \nonumber \]

\[\begin{aligned} x-5 &=0 \\ x &=5 \end{aligned} \nonumber \]

Por lo tanto, las soluciones son$x = −3$ y$x =5$

Comprobar:

Compruebe que cada solución satisfaga la ecuación original.

Sustituto$−3$ de$x$:

\[\begin{aligned}(x+3)(x-5) &=0 \\(-3+3)(-3-5) &=0 \\(0)(-8) &=0 \\ 0 &=0 \end{aligned} \nonumber \]

Sustituto$5$ de$x$:

\[\begin{aligned}(x+3)(x-5) &=0 \\(5+3)(5-5) &=0 \\(8)(0) &=0 \\ 0 &=0 \end{aligned} \nonumber \]

Porque cada cheque produce una declaración verdadera, ambos$x = −3$ y$x = 5$ son soluciones de$(x + 3)(x−5) = 0$.

Ejercicio$\PageIndex{1}$

Resolver para x:$(x-7)(x-2)=0$

Contestar: $7$,$2$

La propiedad cero del producto también funciona igual de bien si hay más de dos factores presentes. Por ejemplo, si$abc = 0$, entonces cualquiera$a = 0$ o$b = 0$ o$c = 0$. Usemos esta idea en el siguiente ejemplo.

Ejemplo$\PageIndex{2}$

Resolver para$x$:$x(2x + 9)(3x−5) = 0$

Solución

El producto de tres factores es igual a cero.

\[x(2x + 9)(3x−5) = 0 \nonumber \]

Usando la propiedad cero del producto, establezca cada factor igual a cero, luego resuelva las ecuaciones resultantes para$x$.

\[x=0 \nonumber \]

\[\begin{align*} 2x + 9 &= 0\\ 2x &= -9\\ x &= -\dfrac{9}{2} \end{align*} \nonumber \]

\[\begin{align*} 3x - 5 &= 0\\ 3x &= 5\\ x &= \dfrac{5}{3} \end{align*} \nonumber \]

De ahí que las soluciones sean$x = 0$,$x = −9/2$, y$x =5 /3$. Animamos al lector a verificar la solución.

Ejercicio$\PageIndex{2}$

Resolver para$x$:$6x(x + 4)(5x + 1) = 0$

Contestar: $0$,$−4$,$−1/5$

Lineal versus no lineal

Todas las ecuaciones resueltas en capítulos anteriores fueron ejemplos de lo que se denominan ecuaciones lineales. Si la mayor potencia de la variable que estamos resolviendo es una, entonces las gráficas involucradas son líneas. De ahí el término, ecuación lineal. No obstante, si el poder en la variable que estamos resolviendo supera uno, entonces las gráficas involucradas son curvas. De ahí el término, ecuación no lineal. En este capítulo aprenderemos a resolver ecuaciones no lineales que involucran polinomios. Sin embargo, primero asegurémonos de que podemos reconocer la diferencia entre una ecuación lineal y una no lineal.

Definición: Ecuaciones lineales versus no lineales

Utilice las siguientes condiciones para determinar si una ecuación es lineal o no lineal.

Si el poder más alto de la variable que estamos resolviendo es uno, entonces la ecuación es lineal.
Si la potencia más alta de la variable para la que estamos resolviendo es mayor que uno, entonces la ecuación es no lineal.

Ejemplo$\PageIndex{3}$

Si la instrucción es “resolver para”$x$, clasifique cada una de las siguientes ecuaciones como lineal o no lineal.

$3x−5=4−7x$
$x^2 =8x$

Solución

Debido a que la instrucción es “resolver para”$x$, para determinar si la ecuación es lineal o no lineal, identificamos la mayor potencia$x$ presente en la ecuación.

El poder más alto del$x$ presente en la ecuación$3x− 5=4− 7x$ es uno. De ahí que esta ecuación sea lineal.
La ecuación$x^2 =8 x$ contiene una potencia$x$ superior a uno (contiene una$x^2$). De ahí que esta ecuación sea no lineal.

Ejercicio$\PageIndex{3}$

Clasifique la siguiente ecuación como lineal o no lineal:$2x = x^3 −4$

Contestar: no lineal

Ahora que podemos clasificar las ecuaciones como lineales o no lineales, introduzcamos estrategias para resolver cada tipo, la primera de las cuales ya debería ser familiar.

Estrategia para resolver una ecuación lineal

Si una ecuación es lineal, inicie el proceso de solución moviendo todos los términos que contienen la variable para la que está resolviendo a un lado de la ecuación, luego mueva todos los términos que no contengan la variable para la que está resolviendo al otro lado de la ecuación.

Ejemplo$\PageIndex{4}$

Resolver para$x$:$3 x−5=4−7x$

Solución

Debido a que la instrucción es “resolver para$x$” y observamos que el mayor poder del$x$ presente es uno, la ecuación$3x−5=4−7x$ es lineal. De ahí que la estrategia sea mover todos los términos que contienen$x$ a un lado de la ecuación, luego mover todos los términos restantes al otro lado de la ecuación.

\[\begin{array}{rlrl}{3 x-5} & {=4-7 x} & {\color {Red} \text { Original equation. }} \\ {3 x-5+7 x} & {=4} & {\color {Red} \text { Add } 7 x \text { to both sides. }} \\ {3 x+7 x} & {=4+5} & {\color {Red} \text { Add } 5 \text { to both sides. }}\end{array} \nonumber \]

Observe cómo hemos logrado mover todos los términos que contienen$x$ a un lado de la ecuación y todos los términos que no contienen$x$ al otro lado de la ecuación.

\[\begin{array}{rlrl}{10 x} & {=9} & {} & {\color {Red} \text { Simplify both sides. }} \\ {x} & {=\dfrac{9}{10}} & {} & {\color {Red} \text { Divide both sides by } 10 .}\end{array} \nonumber \]

De ahí que la solución de$3x−5=4−7x$ es$x =9 /10$. Se anima a los lectores a verificar esta solución.

Ejercicio$\PageIndex{4}$

Agrega texto de ejercicios aquí.

Contestar: $1/4$

La situación es muy diferente cuando la ecuación es no lineal.

Estrategia para resolver una ecuación no lineal

Si una ecuación es no lineal, primero mueve todo a un lado de la ecuación, haciendo que un lado de la ecuación sea igual a cero. Continuar con el proceso de solución factorizando y aplicando la propiedad cero del producto.

Ejemplo$\PageIndex{5}$

Resolver para$x$:$x^2 = 8x$

Solución

Debido a que la instrucción es “resolver para”$x$, y el poder más alto de$x$ es mayor que uno, la ecuación$x^2 =8x$ es no lineal. De ahí que la estrategia requiera que movamos todos los términos a un lado de la ecuación, haciendo que un lado sea cero.

\[\begin{array}{rlrl}{x^{2}} & {=8 x} \quad {\color {Red} \text { Original equation. }} \\ {x^{2}-8 x} & {=0} \quad {\color {Red} \text { Subtract } 8 x \text { from both sides. }}\end{array} \nonumber \]

Observe cómo hemos logrado mover todos los términos a un lado de la ecuación, haciendo que un lado sea igual a cero. Para finalizar la solución, factorizamos el$\mathrm{GCF}$ en el lado izquierdo.

\[x(x-8) = 0 \quad \color {Red} \text {Factor out the GCF.} \nonumber \]

Tenga en cuenta que ahora tenemos un producto de dos factores que equivale a cero. Por la propiedad cero del producto, o bien el primer factor es cero o el segundo factor es cero.

\[\begin{array}{r}{x=0 \quad \text { or } \quad x-8=0} \\ {x=8}\end{array} \nonumber \]

De ahí que las soluciones sean$x = 0$ y$x = 8$.

Comprobar:

Compruebe que cada solución satisfaga la ecuación original.

\[\begin{array}{l}{\text { Substitute } 0 \text { for } x :} \\ {\qquad \begin{aligned} x^{2} &=8 x \\(0)^{2} &=8(0) \\ 0 &=0 \end{aligned}}\end{array} \nonumber \]

\[\begin{array}{l}{\text { Subtitute } 8 \text { for } x :} \\ {\qquad \begin{aligned} x^{2} &=8 x \\(8)^{2} &=8(8) \\ 64 &=64 \end{aligned}}\end{array} \nonumber\]

Nótese que ambos resultados son afirmaciones verdaderas, garantizando que ambos$x = 0$ y$x = 8$ son soluciones de$x^2 =8x$

Ejercicio$\PageIndex{5}$

Resolver para$x$:$x^2 =−5x$

Contestar: $0$,$-5$

¡Advertencia!

¡Lo siguiente es incorrecto!

Considera lo que pasaría si dividiéramos ambos lados de la ecuación$x^2 =8x$ en Ejemplo$\PageIndex{5}$ por$x$:

\[\begin{aligned} x^{2} &=8 x \\ \dfrac{x^{2}}{x} &=\dfrac{8 x}{x} \\ x &=8 \end{aligned} \nonumber \]

Tenga en cuenta que hemos perdido la segunda respuesta que se encuentra en Ejemplo$\PageIndex{5}$,$x = 0$. ¡Este ejemplo demuestra que nunca debes dividir por la variable para la que estás resolviendo! Si lo haces, y se produce la cancelación, perderás respuestas.

Intentemos resolver una ecuación no lineal que requiera factorizar por agrupación.

Ejemplo$\PageIndex{6}$

Resolver para$x$:$6x^2 +9x−8x−12 = 0$

Solución

Debido a que estamos resolviendo$x$ y hay un poder$x$ mayor que uno, esta ecuación es no lineal. De ahí que el primer paso sea mover todo a un lado de la ecuación, haciendo que un lado sea igual a cero. Bueno eso ya está hecho, así que factoricemos el lado izquierdo agrupando. Tenga en cuenta que podemos$3x$ factorizar de los dos primeros términos y$−4$ de los dos segundos términos.

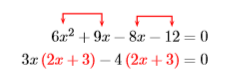
$fig 6.2.a.png$

Factorizar el factor común$2x + 3$.

\[(3x-4){\color {Red}(2x + 3)}=0 \nonumber \]

Ahora tenemos un producto de dos factores que equivale a cero. Utilice la propiedad cero del producto para escribir:

\[\begin{aligned} 3x-4 &=0 \\ 3x &= 4 \\ x &=\dfrac{4}{3} \end{aligned} \nonumber \]

\[\begin{aligned} 2x+3 &=0 \\ 2x &= -3 \\ x &= -\dfrac{3}{2} \end{aligned}\]

De ahí que las soluciones sean$x =4 /3$ y$x =−3/2$.

Comprobar:

Usemos la calculadora gráfica para verificar la solución$x =4 /3$. Primero, almacene la solución$4/3$ en la variable$\mathbb{X}$ usando las siguientes pulsaciones de teclas (vea la primera imagen en la Figura$\PageIndex{1}$.

fig 6.2.b.png — La figura$\PageIndex{1}$ indica que la expresión$6x^2 +9x−8x−12$ es igual a cero cuando$x =4 /3$.

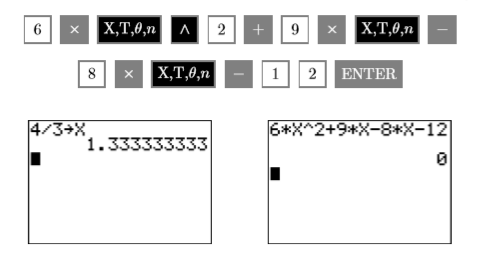
higo 6.2.1.png — Figura$\PageIndex{1}$: Comprobando la solución$x =4 /3$.

Por lo tanto, la solución$x =4 /3$ comprueba. Se anima a los lectores a utilizar sus calculadoras gráficas para verificar la segunda solución,$x = −3/2$.

Ejercicio$\PageIndex{6}$

Resolver para$x$:$5x^2 −20x−4x + 16 = 0$

Contestar: $4/5$,$4$

Uso de la Calculadora Gráfica

En esta sección vamos a emplear dos rutinas de calculadora diferentes para encontrar la solución de una ecuación no lineal. Antes de recoger la calculadora, usemos primero un método algebraico para resolver la ecuación$x^2 = −5x$. La ecuación es no lineal, por lo que el primer paso es mover todo a un lado de la ecuación, haciendo que un lado sea igual a cero.

\[\begin{aligned} x^{2} &= -5x \quad \color {Red} \text { Nonlinear. Make one side zero. } \\ x^{2}+5 x &= 0 \quad \color {Red} \text { Add } 5x \text { to both sides. } \\ x(x+5) &= 0 \quad \color {Red} \text { Factor out the GCF. } \end{aligned} \nonumber \]

Utilice la propiedad cero del producto, estableciendo cada factor igual a cero y luego resolviendo las ecuaciones resultantes para$x$.

\[x=0 \nonumber \]

\[\begin{aligned} x+5&=0 \\ x&=-5 \end{aligned} \nonumber \]

De ahí que las soluciones sean$x = 0$ y$x = −5$.

Ahora usaremos la calculadora para encontrar las soluciones de$x^2 = −5x$. La primera técnica emplea la rutina 5:intersect en el menú CALC de la calculadora.

Ejemplo$\PageIndex{7}$

Utilice la utilidad 5:intersect en la calculadora gráfica para resolver la ecuación$x^2 = −5x$ para$x$.

Solución

Cargue el lado izquierdo de$x^2 = −5x$ adentro$\mathbb{Y1}$ y el lado derecho adentro$\mathbb{Y2}$ (vea la Figura$\PageIndex{2}$). Al seleccionar 6:ZStandard del menú ZOOM se obtienen los gráficos mostrados en la imagen de la derecha en la Figura$\PageIndex{2}$.

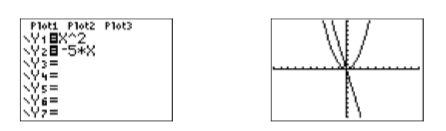
higo 6.2.2.png — Figura$\PageIndex{2}$: Esbozar las gráficas de cada lado de la ecuación$x^2 = −5x$.

Tenga en cuenta que la gráfica de$y = x^2$ es una parábola que se abre hacia arriba, con vértice (punto de inflexión) en el origen. Esta gráfica revela por qué la ecuación$x^2 = −5x$ se llama una ecuación no lineal (no todas las gráficas involucradas son líneas). A continuación, la gráfica de$y = −5x$ es una línea con pendiente$−5$ e$y$ -intercepción en el origen.

Obviamente, las dos gráficas se cruzan en el origen, pero también parece que puede haber otro punto de intersección que esté en la pantalla. Aumentemos$\mathbb{Ymax}$ en un intento de revelar el segundo punto de intersección. Después de cierta experimentación, los ajustes mostrados en la primera imagen de la Figura$\PageIndex{3}$ revelan ambos puntos de intersección. Al presionar el botón GRAPAR se produce la imagen de la derecha en la Figura$\PageIndex{3}$.

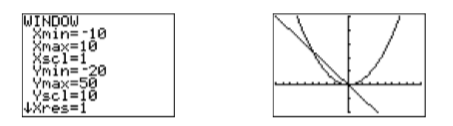
higo 6.2.3.png — Figura$\PageIndex{3}$: Ajuste los parámetros de **VENTANA** para revelar ambos puntos de intersección.

Para encontrar las soluciones de la ecuación$x^2 =−5x$, debemos encontrar las coordenadas de los puntos donde se$y = −5x$ cruzan$y = x^2$ las gráficas. La$x$ coordenada -de cada punto de intersección será una solución de la ecuación$x^2 = −5x$.

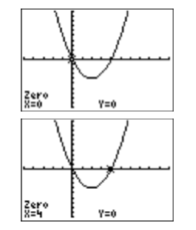
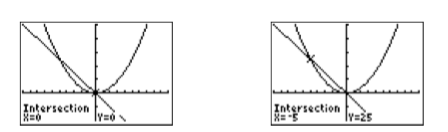
Comience por seleccionar 5:intersectar en el menú CALC. Cuando se le solicite la “Primera curva?” , pulse INTRO. Cuando se le solicite la “¿Segunda curva?” , pulse INTRO. Cuando se le solicite un “Adivina”, presione ENTRAR. El resultado es el punto que$(0,0)$ se muestra en la imagen de la izquierda en la Figura$\PageIndex{4}$.
Repita el proceso por segunda vez. Seleccione 5:intersectar en el menú CALC. Cuando se le solicite la “Primera curva?” , pulse INTRO. Cuando se le solicite la “¿Segunda curva?” , pulse INTRO. Cuando se le solicite un “Adivina”, use la tecla de flecha izquierda para acercar el cursor al punto de intersección más a la izquierda y, a continuación, presione ENTRAR. El resultado es el punto que$(−5,25)$ se muestra en la imagen de la derecha en la Figura$\PageIndex{4}$.

higo 6.2.4.png — Figura$\PageIndex{4}$: Utilice la utilidad 5:intersect para encontrar los puntos de intersección.

Reportando la solución en tu tarea:

Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

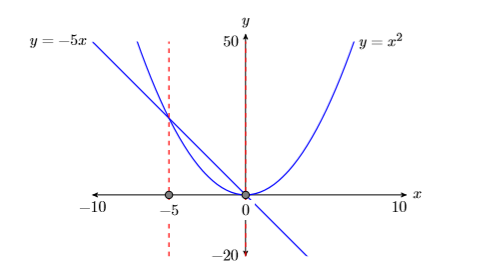
higo 6.2.5.png — Figura$\PageIndex{5}$: Reportando tu solución gráfica en tu tarea.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{5}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{5}$).
Etiquetar cada gráfica con su ecuación (ver Figura$\PageIndex{5}$).
Coloque líneas verticales discontinuas a través de cada punto de intersección. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$x^2 =−5x$ (ver Figura$\PageIndex{5}$).

De ahí que las soluciones de$x^2 = −5x$ son$x = −5$ y$x = 0$. Observe ahora estos coinciden con las soluciones encontradas usando la técnica algebraica.

Ejercicio$\PageIndex{7}$

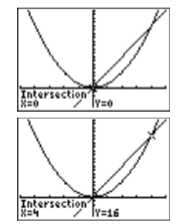
Utilice la utilidad 5:intersect en la calculadora gráfica para resolver la ecuación$x^2 =4x$ para$x$.

Contestar: $Ejercicio 6.2.4.png$

Antes de demostrar una segunda técnica de calculadora gráfica para resolver ecuaciones no lineales, tomemos un momento para recordar la definición de un cero de una función, la cual fue presentada por primera vez en el Capítulo 5, Sección 3.

Ceros y$x$-intercepts

Los puntos donde la gráfica de$f$ cruza el$x$ eje -se denominan las$x$ -intercepciones de la gráfica de$f$. El$x$ -valor de cada$x$ -intercepción se llama cero de la función$f$.

Ahora vamos a emplear la utilidad 2:cero del menú CALC para encontrar las soluciones de la ecuación$x^2 = −5x$.

Ejemplo$\PageIndex{8}$

Utilice la utilidad 2:cero en la calculadora gráfica para resolver la ecuación$x^2 = −5x$ para$x$.

Solución

Primero, hacer que un lado de la ecuación sea igual a cero.

\[\begin{aligned}x^{2} &=-5 x \quad \color {Red} \text { Make one side zero. } \\ x^{2}+5 x &=0 \quad \color {Red} \text { Add } 5 x \text { to both sides. }\end{aligned} \nonumber \]

Para determinar los valores de$x$ esa marca$x^2 +5x = 0$, debemos ubicar los puntos donde la gráfica de$f(x)=x^2 +5x$ cruza el$x$ eje -eje. Estos puntos son las$x$ -intercepciones de la gráfica de$f$ y los$x$ -valores de estos puntos son los ceros de la función$f$.

Cargue la función$f(x)=x^2 +5 x$ en$\mathbb{Y1}$, luego seleccione 6:ZStandard para producir la imagen en la Figura$\PageIndex{6}$. Tenga en cuenta que la gráfica de$f$ tiene dos$x$ -intercepciones, y los$x$ -valores de cada uno de estos puntos son los ceros de la función$f$.

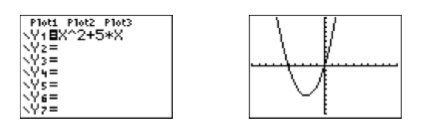
higo 6.2.6.png — Figura$\PageIndex{6}$: Esbozar la gráfica de$p(x)=x^2 +5x$.

Nota

A menudo es más fácil encontrar las soluciones de una ecuación no lineal haciendo un lado cero e identificando dónde cruza el$x$ eje la gráfica de la función resultante.

Seleccione 2:cero en el menú CALC (ver Figura$\PageIndex{7}$).

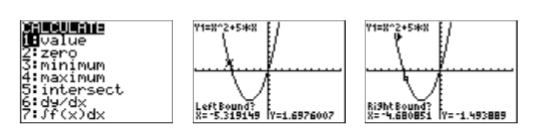
higo 6.2.7.png — Figura$\PageIndex{7}$: Establecer los límites izquierdo y derecho al usar la utilidad **2:zero** para encontrar las$x$ intercepciones -de la gráfica de$f(x)=x^2 +5x$.

La calculadora responde pidiendo un “¿Izquierda?” Use la tecla de flecha izquierda para mover el cursor de manera que quede a la izquierda de la$x$ intersección cercana$(−5,0)$ (vea la segunda imagen en la Figura$\PageIndex{7}$), luego presione la tecla ENTRAR.
La calculadora responde pidiendo un “¿Encuadernado a la derecha?” Mueva el cursor para que quede ligeramente a la derecha de la intersección x cerca$(−5,0)$ (vea la tercera imagen Figura$\PageIndex{7}$), luego presione la tecla ENTRAR.
La calculadora responde pidiendo un “¿Adivina?” Observe las dos marcas triangulares cerca de la parte superior de la ventana de visualización en la primera imagen de la Figura$\PageIndex{8}$ que marcan los límites izquierdo y derecho. Siempre y cuando coloque el cursor de manera que el valor x de la ubicación del cursor se encuentre entre estas dos marcas, ha hecho una suposición válida. Debido a que el cursor ya se encuentra entre estas dos marcas, normalmente lo dejamos donde está y presionamos la tecla ENTRAR.

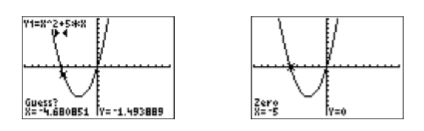
higo 6.2.8.png — Figura$\PageIndex{8}$: *Establecer el límite correcto y hacer una suposición.*

Después de hacer su suposición y presionar la tecla ENTER, la calculadora procede a encontrar una aproximación de la$x$ -intercepción que se encuentra entre los límites izquierdo y derecho previamente marcados (ver la segunda imagen en la Figura$\PageIndex{8}$. De ahí que esta$x$ -intercepción sea$(−5,0)$, haciendo$−5$ un cero de$f(x)=x^2 +5x$ y una solución de la ecuación$x^2 +5x = 0$.

Dejaremos a nuestros lectores repetir el proceso 2:cero para encontrar el segundo cero en el origen.

Reportando la solución en tu tarea:

Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{9}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{9}$).
Etiquetar cada gráfica con su ecuación (ver Figura$\PageIndex{9}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intersección. Sombra y etiquete los$x$ -valores de cada$x$ -intercepción. Estas son las soluciones de la ecuación$x^2 = −5x$ (ver Figura$\PageIndex{9}$).

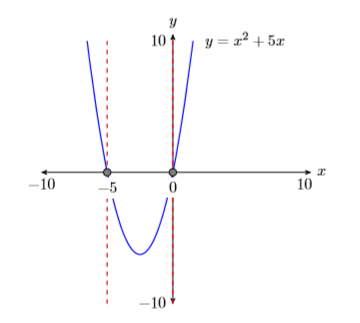
higo 6.2.9.png — Figura$\PageIndex{9}$: Reportando tu solución gráfica en tu tarea.

De ahí que las soluciones de$x^2 = −5x$ son$x = −5$ y$x = 0$. Observe lo bien que esto concuerda con las soluciones encontradas usando la técnica algebraica y las soluciones encontradas usando la utilidad 5:intersect en Example$\PageIndex{7}$.

Ejercicio$\PageIndex{8}$

Utilice la utilidad 2:cero en la calculadora gráfica para resolver la ecuación$x^2 =4x$ para$x$.

Contestar: $Ejercicio 6.2.8.png$

Search

Text Color

Text Size

Margin Size

Font Type