6.4: Factorización ax² + bx + c cuando a≠ 1

Última actualización
Guardar como PDF

Page ID: 111694

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección seguimos factorizando trinomios de la forma$ax^2 + bx + c$. En la última sección, todos nuestros ejemplos tenían$a = 1$, y pudimos “Drop in place” nuestro par entero en un círculo. No obstante, en esta sección$a \neq 1$,, y pronto veremos que no podremos utilizar la técnica de “Drop in place”. No obstante, a los lectores les complacerá saber que el$ac$ método -seguirá aplicándose.

Ejemplo$\PageIndex{1}$

Factor:$2x^2 −7x−15$.

Solución

Procedemos de la siguiente manera:

Comparar$2x^2 −7x−15$$ax^2 + bx + c$ e identificar$a = 2$,$b = −7$, y$c = −15$. Obsérvese que el principal principal es$a = 2$, por lo que este caso es diferente de todos los casos discutidos en la Sección 6.3.
Calcular$ac$. Tenga en cuenta que$ac = (2)(−15)$, entonces$ac = −30$.
Listar todos los pares enteros cuyo producto es$ac =−30$. \[\begin{array}{ll}{1,-30} & {-1,30} \\ {2,-15} & {-2,15} \\ {3,-10} & {-3,10} \\ {5,-6} & {-5,6}\end{array} \nonumber \]
Encierra en círculo el par ordenado cuya suma es$b =−7$. \[\begin{array}{cc}{1,-30} & {-1,30} \\ {2,-15} & {-2,15} \\ {\color {Red}3,-10} & {-3,10} \\ {5,-6} & {-5,6}\end{array} \nonumber \]
Tenga en cuenta que si “dejamos caer en su lugar” nuestro par ordenado en un círculo,$(x+3)(x-10) \neq 2x^2-7x-15$. A la derecha del murciélago, el producto de los términos en la posición “Primera” no es igual$2x^2$. En cambio, dividimos el término medio de$2x^2 −7x−15$ en una suma de términos similares usando nuestro par de números enteros en un círculo$3$ y$−10$. \[2x^2{\color {Red}-7x}-15 = 2x^2{\color {Red}+3x-10x}-15 \nonumber \]Ahora factorizamos por agrupación. Factor$x$ de los dos primeros términos y de$−5$ los dos segundos términos. \[= x(2x + 3)−5(2x + 3) \nonumber \]Ahora podemos factorizar (2x + 3). \[=(x−5)(2x + 3) \nonumber \]
Usa el atajo FOIL para verificar mentalmente tu respuesta. Para multiplicar$(x−5)(2x + 3)$, usa estos pasos:
- Multiplicar los términos en las posiciones “Primera”:$2x^2$.
- Multiplicar los términos en las posiciones “Exterior” e “Interior” y combinar los resultados mentalmente:$3x−10x = −7x$.
- Multiplicar los términos en las “Últimas” posiciones:$−15$. Es decir:\[(x-5)(2x+3)=\begin{array}{ccccccc} \color {Red}F & & \color {Red}O & & \color {Red}I & & \color {Red}L \\ 2x^2&+&3x&-&10x&-&15 \end{array} \nonumber \]

Combinando términos similares,$(x − 5)(2x + 3) = 2x^2 − 7x − 15$, que es el trinomio original, así que nuestra solución comprueba. Tenga en cuenta que si combina los productos “Exterior” e “Interior” mentalmente, el cheque va aún más rápido.

Ejercicio$\PageIndex{1}$

Factor:$3x^2 + 13x + 14$

Responder: $(x + 2)(3x + 7)$

Acelerar un poco las cosas

Algunos lectores ya podrían estar preguntando “¿De verdad tengo que enumerar todos esos pares ordenados si ya veo el par que necesito?” La respuesta es “¡No!” Si ves el par que necesitas, úsalo para romper el término medio del trinomio como una suma de términos similares.

Ejemplo$\PageIndex{2}$

Factor:$3x^2 −7x−6$.

Solución

Compare$3x^2−7x−6$ con$ax^2+bx+c$ y tenga en cuenta que$a = 3$,$b =−7$, y$c = −6$. Calcular$ac = (3)(−6)$, entonces$ac = −18$. Ahora, ¿se te ocurre un par entero cuyo producto es$ac = −18$ y cuya suma es$b = −7$? Para algunos, la pareja simplemente se les viene a la cabeza:$2$ y$−9$. Divida el término medio en una suma de términos similares usando el par$2$ y$−9$.

\[\begin{align*} 3x^2{\color {Red}-7x}-6 &= 3x^2{\color {Red}+2x-9x}-6 \quad \color {Red} -7x=2x-9x\\ &= x(3x+2)-3(3x+2) \quad \color {Red} \text {Factor by grouping.}\\ &= (x-3)(3x+2) \quad \color {Red} \text {Factor out} (3x+2). \end{align*} \nonumber \]

Usa el atajo FOIL para verificar tu respuesta.

\[(x-3)(3x+2)=\begin{array}{ccccccc} \color {Red}F & & \color {Red}O & & \color {Red}I & & \color {Red}L \\ 3x^2&+&2x&-&9x&-&6 \end{array} \nonumber \]

Combinando términos similares$(x−3)(3x+2) = 3x^2−7x−6$,, el trinomio original. Nuestra solución comprueba. Tenga en cuenta que si combina los productos “Exterior” e “Interior” mentalmente, el cheque va aún más rápido.

Ejercicio$\PageIndex{2}$

Factor:$2x^2 −9x + 10$

Contestar: $(x−2)(2x−5)$

Por otro lado, algunos lectores podrían estar diciendo “Bueno, el par ordenado necesario no me está metiendo en la cabeza. ¿Tengo una manera de recortar la obra?” La respuesta es “¡Sí!” Como estás listando los pares ordenados cuyo producto es igual$ac$, ten en cuenta que necesitas el par pedido cuya suma es$b$. Si tropieza con el par necesario, detenga el proceso de listado y “coloque” su par ordenado en su lugar.

Ejemplo$\PageIndex{3}$

Factor:$3x^2 −33x + 54$.

Solución

Compare$3x^2 −33x + 54$ con$ax^2 + bx + c$ y tenga en cuenta que$a = 3$,$b = −33$, y$c = 54$. Calcular$ac = (3)(54)$, entonces$ac = 162$. ¡Ay! ¡Ese es un gran número! Sin embargo, empieza a enumerar los pares enteros cuyo producto es$ac = 162$, pero ten en cuenta que necesitas un par entero cuya suma sea$b = −33$.

\[\begin{array}{ll}{1,162} \\ {2,81} \\ {3,54} \\ {6,27} & {\color {Red}-6,-27}\end{array} \nonumber\]

Tan pronto como anotamos el par$6$ y$27$, nuestra mente dijo “la suma de$6$ y$7$ es”$33$. No obstante, necesitamos que la suma sea igual$b = −33$, así que encajamos$−6$ y$−27$ en su lugar. A continuación, separamos el término medio en una suma de términos similares usando nuestro par circular.

\[\begin{align*} 3x^2{\color {Red}-33x}-54 &= 3x^2{\color {Red}-6x-27x}-54 \quad \color {Red} -33x=-6x-27x\\ &= 3x(x-2)-27(x-2) \quad \color {Red} \text {Factor by grouping.}\\ &= (3x-27)(x-2) \quad \color {Red} \text {Factor out} (x-2). \end{align*} \nonumber\]

¡Oh, oh! Ahora nos damos cuenta de que podemos$3$ factorizar de cada término en el primer factor!

\[= 3(x−9)(x−2) \nonumber \]

Nos perdimos sacar el$\mathrm {GCF}$! Vamos a intentarlo de nuevo, solo que esta vez hagamos lo que siempre se supone que debemos hacer en el primer paso: Factorizar el$\mathrm {GCF}$.

\[3x^2 −33x + 54 = 3(x^2 −11x + 18) \nonumber \]

Comparando$x^2 − 11x + 18$ con$ax^2 + bx + c$, vemos eso$a = 1$,$b = −11$, y$c = 18$. Necesitamos un par entero cuyo producto es$ac = 18$ y cuya suma es$b = −11$. Tenga en cuenta que estos números son considerablemente más pequeños que los números con los que tuvimos que lidiar cuando olvidamos por primera vez el factor$\mathrm {GCF}$. Debido a que los números son más pequeños, el par entero$−9$ y$−2$ fácilmente viene a la mente. Además, porque$a = 1$, podemos factorizar simplemente$x^2 − 11x + 18$ dejando caer el par entero$−9$ y$−2$ en su lugar.

\[3(x2 −11x + 18) = 3(x−9)(x−2) \nonumber \]

¡Una solución mucho más simple!

Ejercicio$\PageIndex{3}$

Factor:$5x^2 −35x−40$

Contestar: $5( x−8)(x + 1)$

En Ejemplo$\PageIndex{3}$, vimos cuánto más difícil hacíamos el problema olvidándonos de factorizar primero el mayor factor común ($\mathrm {GCF}$). Tratemos de no volver a cometer ese error.

Primera regla de factorización

El primer paso para factorizar cualquier polinomio es factorizar el mayor factor común.

Ejemplo$\PageIndex{4}$

Factor:$30x^3 −21x^2 −18x$.

Solución

Tenga en cuenta que el$\mathrm {GCF}$ de$30x^3$$21x^2$,, y$18x$ es$3x$. Factorizar esto$\mathrm {GCF}$.

\[\begin{align*} 30x^3-21x^2-18x &= {\color{Red}3x}\cdot 10x^2-{\color{Red}3x}\cdot 7x -{\color{Red}3x}\cdot 6\\ &= {\color{Red}3x}(10x^2-7x-6) \end{align*} \nonumber \]

A continuación, compare$10x^2 −7x−6$ con$ax^2 + bx + c$ y tenga en cuenta que$a = 10$$b =−7$,, y$c = −6$. Empieza a enumerar los pares enteros cuyo producto es$ac = −60$, pero ten en cuenta que necesitas un par entero cuya suma sea$b = −7$.

\[\begin{array}{ll}{1,-60} \\ {2,-30} \\ {3,-20} \\ {4,-15} \\ {\color {Red}5,-12}\end{array} \nonumber\]

Divida el término medio en una suma de términos similares usando nuestro par circular.

\[\begin{align*} 3x(10x^2-7x-6) &= 3x(10x^2+5x-12x-18) \quad \color {Red} -7x=5x-12x\\ &= 3x[5x(2x+1)-6(2x+1)] \quad \color {Red} \text {Factor by grouping.}\\ &= 3x(5x-6)(2x+1) \quad \color {Red} \text {Factor out} (2x+1). \end{align*} \nonumber\]

De ahí,$30x^3 −21x^2 −18x =3x(5x−6)(2x + 1)$.

Comprobar: Primero, usa el atajo FOIL para multiplicar los dos factores binomiales, luego distribuir el factor monomio.

\[\begin{align*} 3x(5x-6)(2x + 1) &= 3x(10x^2-7x-6) \quad \color {Red} \text {Apply the FOIL shortcut}\\ &= 3x^3-21x^2-18x \quad \color {Red} \text {Distribute the } 3x. \end{align*} \nonumber\]

Debido a que este es el polinomio original, la solución comprueba.

Ejercicio$\PageIndex{4}$

Factor:$12x^4 +2x^3 −30x^2$

Contestar: $2x^2(3x+5)(2x−3)$

Ecuaciones no lineales revisitadas

Usemos la técnica de factorización de este capítulo para resolver algunas ecuaciones no lineales.

Ejemplo$\PageIndex{5}$

Resuelve la ecuación$2x^2 = 13 x−20$ tanto algebraica como gráficamente, luego compara tus respuestas.

Solución

Debido a que hay una potencia de x mayor que uno, la ecuación es no lineal. Hacer un lado igual a cero.

\[\begin{align*} 2x^2 &= 13x-20 \quad \color {Red} \text {Original equation}\\2x^2-13x+20 &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber\]

Compare$2x^2 −13x + 20$ con$ax^2 + bx + c$ y tenga en cuenta que$a = 2$,$b = −13$ y$c = 20$. Necesitamos un par entero cuyo producto es$ac = 40$ y cuya suma es$b = −13$. El par entero$−5$ y$−8$ viene a la mente. Escribe el término medio como una suma de términos similares usando este par.

\[\begin{align*} 2x^2-5x-8x+20 &= 0 \quad \color {Red} -13x=-5x-8x\\x(2x-5)(2x-5) &= 0 \quad \color {Red} \text {Factor by grouping.}\\(x-4)(2x-5) &= 0 \quad \color {Red} \text {Factor out } 2x-5 \end{align*} \nonumber\]

Tenemos un producto que equivale a cero. Utilice la propiedad cero del producto para completar la solución.

\[\begin{align*} x-4 &= 0 \\x & = 4 \end{align*} \nonumber\]

\[\begin{align*} 2x-5 &= 0 \\2x & = 5\\x & = \dfrac{5}{2} \end{align*} \nonumber\]

Así, las soluciones de$2x^2 = 13x−20$ son$x = 4$ y$x =5 /2$.

Solución gráfica:

Cargue cada lado de la ecuación$2x^2 = 13x−20$ en el menú Y= de su calculadora gráfica,$y =2x^2$ en$\mathbb{Y1}$,$y = 13 x−20$ en$\mathbb{Y2}$

(ver Figura$\PageIndex{1}$). Seleccione 6:ZStandard en el menú ZOOM para producir la imagen de la izquierda en la Figura 6.18. Sin embargo, incluso después de ajustar los parámetros WINDOW ($\mathbb{Xmin} =−10$$\mathbb{Xmax} = 10$$\mathbb{Ymin} = −10$,,, y$\mathbb{Ymax} = 60$), la imagen resultante de presionar el botón GRAPH (ver la imagen de la derecha en la Figura$\PageIndex{1}$) no muestra claramente los dos puntos de intersección.

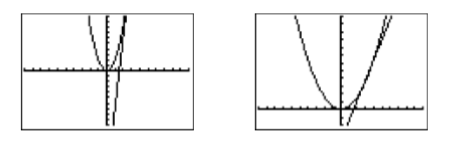
higo 6.4.1.png — Figura$\PageIndex{1}$: Croquis$y =2x^2$ y$y = 13x−20$.

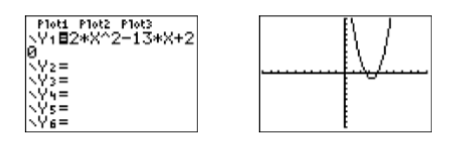
Cambiemos nuestra estrategia y trabajemos con la ecuación$2x2 −13x + 20 = 0 $ en su lugar. Cargue$y =2x^2 − 13x + 20$$\mathbb{Y1}$ en en el menú Y=, luego seleccione 6:ZStandard en el menú ZOOM para producir la imagen a la derecha en la Figura$\PageIndex{2}$.

higo 6.4.2.png — Figura$\PageIndex{2}$: Croquis$y =2x^2 −13x + 20$.

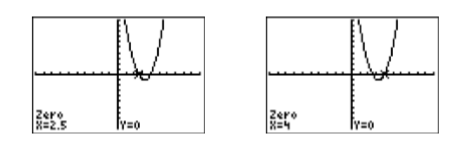
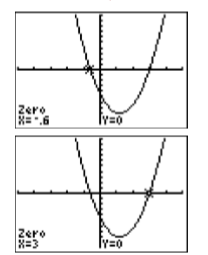
Para encontrar las soluciones de$2x^2−13x+20 = 0$, debemos identificar las$x$ -intercepciones de la gráfica en la Figura$\PageIndex{1}$. Seleccione 2:cero en el menú CALC, luego mueva las flechas izquierda y derecha=para mover el cursor a la izquierda de la primera$x$ intersección. Presione ENTRAR para marcar el “Límite izquierdo”, luego mueva el cursor a la derecha$x$ de la intersección y presione ENTRAR para marcar el “Límite derecho”. Por último, presiona ENTRAR para usar la posición actual del cursor para tu “Guess”. El resultado se muestra en la imagen de la izquierda en la Figura$\PageIndex{3}$. Repita el proceso para encontrar la$x$ intercepción más a la derecha. El resultado se muestra en la imagen de la derecha en la Figura$\PageIndex{3}$.

higo 6.4.3.png — Figura$\PageIndex{3}$: Use **2:cero** del menú **CALC** para encontrar las$x$ intercepciones.

Reportando la solución en tu tarea:

Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{4}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{4}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{4}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intercepción. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$2x^2 − 13x + 20 = 0$ (ver Figura$\PageIndex{4}$).

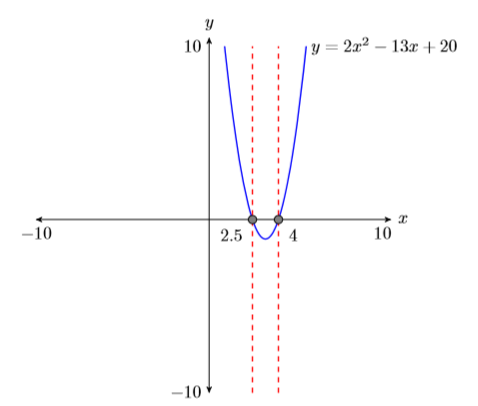
higo 6.4.4.png — Figura$\PageIndex{4}$: Reportando tu solución gráfica en tu tarea.

Finalmente, observe cómo las soluciones gráficas de$2x^2−13x+20=0$, es decir$x =2.5$ y$x = 4$, coinciden con las soluciones$x =5 /2$ y$x = 4$ se encuentran utilizando el método algebraico. Esto es evidencia sólida de que ambos métodos de solución son correctos. Sin embargo, no está de más verificar las respuestas finales en la ecuación original, sustituyendo$5/2$ por$x$ y$4$ para$x$.

\ [\ begin {align*}
2x^2 &= 13x-20\
2\ izquierda (\ dfrac {5} {2}\ derecha) ^2 & = 13\ izquierda (\ dfrac {5} {2}\ derecha) -20\\
2\ izquierda (\ dfrac {25} {4}\ derecha) & = 13\ izquierda (\ dfrac {5} {2} derecha) -20\\
\ dfrac {25} {2} & =\ dfrac {65} {2} -\ dfrac {40} {2}
\ end {align*}\ nonumber\]

\[\begin{align*} 2x^2 &= 13x-20 \\ 2(4)^2 & = 13(4) -20\\ 2(16) & = 13(4) -20\\ 32 & = 52 - 20 \end{align*} \nonumber\]

Porque las dos últimas afirmaciones son afirmaciones verdaderas, las soluciones$x =5 /2$ y$x = 4$ verifican la ecuación original$2x^2 = 13x−20$.

Ejercicio$\PageIndex{5}$

Resuelve la ecuación$5x^2 = 12x + 9$ tanto algebraica como gráficamente, luego compara tus respuestas.

Contestar

$-3/5$,$3$

$Ejercicio 6.4.5.png$

Ejemplo$\PageIndex{6}$

Resuelve la ecuación$2x^3 + x^2 = 28x$ tanto algebraica como gráficamente, luego compara tus respuestas.

Solución

Debido a que hay una potencia de x mayor que uno, la ecuación es no lineal. Hacer un lado igual a cero.

\[\begin{align*} 2x^3+x^2 &= 28x \quad \color {Red} \text {Original equation}\\2x^3+x^2-28x &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber\]

Tenga en cuenta que el$\mathrm {GCF}$ de$2x^3$$x^2$,, y$28x$ es$x$. Factorizar hacia fuera$x$.

\[x(2x^2 + x−28) = 0 \quad \color {Red} \text {Factor out the GCF} \nonumber \]

Compare$2x^2+x−28$ con$ax^2+bx+c$ y tenga en cuenta que$a = 2$,$b = 1$ y$c = −28$. Necesitamos un par entero cuyo producto es$ac = −56$ y cuya suma es$b = 1$. El par entero$−7$ y$8$ viene a la mente. Escribe el término medio como una suma de términos similares usando este par.

\[\begin{align*} x(2x^2-7x+8x-28) &= 0 \quad \color {Red} x=-7x+8x\\x[x(2x-7)+4(2x-7)] &= 0 \quad \color {Red} \text {Factor by grouping.}\\x(x+4)(2x-7) &= 0 \quad \color {Red} \text {Factor out } 2x-7. \end{align*} \nonumber\]

Tenemos un producto de tres factores que equivale a cero. Por la propiedad cero del producto, al menos uno de los factores debe ser igual a cero.

\[x=0 \nonumber \]

\[\begin{align*} x+4 &= 0 \\x & = -4 \end{align*} \nonumber\]

\[\begin{align*} 2x-7 & = 0 \\ 2x & = 7\\ x & = \dfrac{7}{2} \end{align*} \nonumber\]

Así, las soluciones de$2x^3 + x^2 = 28x$ son$x = 0$,$x =−4$, y$x =7 /2$.

Solución gráfica:

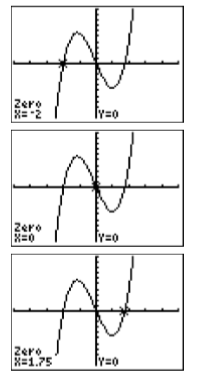
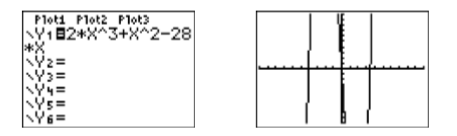
En lugar de trabajar con$2x^3+x^2 = 28x$, graficar cada lado por separado y determinar dónde se cruzan las gráficas, trabajaremos en su lugar con$2x^3 + x^2 − 28x = 0$, ubicando donde la gráfica de$y =2x^3 + x^2 − 28x$ cruza el$x$ eje. Cargue$y =2x^3 + x^2 −28x$$\mathbb{Y1}$ en en el menú Y=, luego seleccione 6:ZStandard en el menú ZOOM para producir la imagen a la derecha en la Figura$\PageIndex{5}$.

higo 6.4.5.png — Figura$\PageIndex{5}$: Croquis$y =2x^3 + x^2 −28x$.

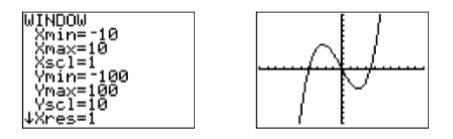
En la imagen de la derecha en la Figura$\PageIndex{6}$, vimos la gráfica elevarse desde la parte inferior de la pantalla, salir de la parte superior de la pantalla, regresar y salir por la parte inferior de la pantalla, y luego finalmente regresar y salir por la parte superior de la pantalla. Claramente, hay al menos dos puntos de inflexión en la gráfica que no son visibles en la ventana de visualización actual. Establezca los ajustes de VENTANA como se muestra en la imagen de la izquierda en la Figura$\PageIndex{6}$, luego presione el botón GRAPADO para producir la imagen a la derecha en la Figura$\PageIndex{6}$. Tenga en cuenta que esta ventana ahora muestra las$x$ -intercepciones así como los puntos de inflexión de la gráfica del polinomio.

higo 6.4.6.png — Figura$\PageIndex{6}$: Ajustar la vista para que los puntos de inflexión del polinomio sean visibles.

Para encontrar las soluciones de$2x^3 + x2 −28x = 0$, debemos identificar las$x$ -intercepciones de la gráfica en la Figura$\PageIndex{6}$. Seleccione 2:cero en el menú CALC, luego use las teclas de flecha izquierda y derecha para mover el cursor a la izquierda$x$ de la primera intersección. Presione ENTRAR para marcar el “Límite izquierdo”, luego mueva el cursor a la derecha$x$ de la intersección y presione ENTRAR para marcar el “Límite derecho”. Por último, presiona ENTRAR para usar la posición actual del cursor para tu “Guess”. El resultado se muestra en la primera imagen de la izquierda en la Figura$\PageIndex{7}$. Repita el proceso para encontrar las restantes$x$ -intercepciones. Los resultados se muestran en las siguientes dos imágenes de la Figura$\PageIndex{7}$.

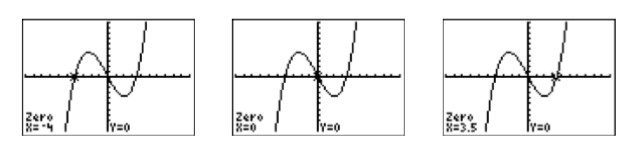
higo 6.4.7.png — Figura$\PageIndex{7}$: Use **2:cero** del menú **CALC** para encontrar las$x$ intercepciones.

Reportando la solución en tu tarea:

Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{8}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{8}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{8}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intercepción. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje -eje. Estas son las soluciones de la ecuación$2x^3 + x^2 −28x = 0$ (ver Figura$\PageIndex{8}$).

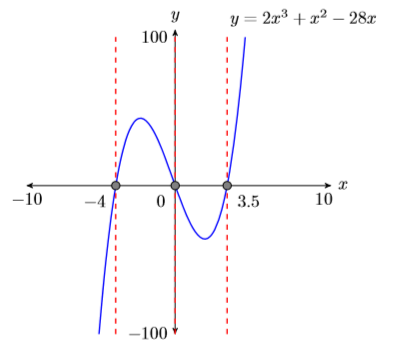
higo 6.4.8.png — Figura$\PageIndex{8}$: Reportando tu solución gráfica en tu tarea.

Finalmente, observe cómo las soluciones gráficas de$2x^3+x^2−28x = 0$, es decir$x =−4$,$x = 0$, y$x =3.5$, coinciden con las soluciones$x = −4$,$x = 0$, y$x =7 /2$ se encuentran usando el método algebraico.

Ejercicio$\PageIndex{6}$

Resuelve la ecuación$4x^3 = −x^2 + 14x$ tanto algebraica como gráficamente, luego compara tus respuestas.

Contestar

$−2$,$0$,$7/4$

$Ejercicio 6.4.6.png$