6.5: Factorización de Formas Especiales

Última actualización
Guardar como PDF

Page ID: 111695

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección repasamos dos formas especiales de producto que aprendimos en el Capítulo 5, la primera de las cuales fue cuadrar un binomio.

Cuadrando un binomio

Aquí hay dos reglas anteriores para cuadrar un binomio.

$(a + b)^2 = a^2 +2ab + b^2$
$(a−b)^2 = a^2 −2ab + b^2$

Trinomios Cuadrados Perfectos

Para cuadrar un binomio tal como$(a + b)^2$, proceder de la siguiente manera:

Cuadrando el primer término:$a$
Multiplique el primer y segundo término, luego doble:$2ab$
Cuadrar el último término:$b^2$

Ejemplo$\PageIndex{1}$

Ampliar:$(2x +3y)^2$

Solución

Usando el patrón$(a+b)^2 = a^2+2ab+b^2$, podemos expandirnos de$(2x+3y)^2$ la siguiente manera:

\[\begin{align*} (2x +3y)^2 &= (2x)^2 + 2(2x)(3y) + (3y)^2 \\ &= 4x^2 +6xy +9y^2 \end{align*} \nonumber \]

Observe cómo cuadramos el primer y segundo término, luego producimos el término medio de nuestra respuesta multiplicando el primer y segundo términos y duplicando.

Ejercicio$\PageIndex{1}$

Ampliar:$(5a +2b)^2$

Contestar: $25a^2 + 20ab +4b^2$

Ejemplo$\PageIndex{2}$

Ampliar:$(3u^2 −5v2)^2$

Solución

Usando el patrón$(a−b)^2 = a^2−2ab+b^2$, podemos expandirnos de$(3u^2−5v^2)^2$ la siguiente manera:

\[\begin{align*} (3u^2 -5v^2)^2 &= (3u^2)^2 - 2(3u^2)(5v^2) + (5v^2)^2 \\ &= 9u^4 - 30u^2v^2 + 25v^4 \end{align*} \nonumber \]

Tenga en cuenta que el signo del término medio es negativo en esta ocasión. El primer y último término siguen siendo positivos porque estamos cuadrando.

Ejercicio$\PageIndex{2}$

Ampliar:$(2s^3 −7t)^2$

Contestar: $4s^6 −28s^3t + 49t^2$

Una vez que hayas cuadrado algunos binomios, es momento de hacer todo el trabajo en tu cabeza.

Cuadrar el primer término.
Multiplica el primer y segundo término y duplica el resultado.
Cuadrar el segundo término.

Ejemplo$\PageIndex{3}$

Amplíe cada una de las siguientes opciones:

$(2y−3)^2$
$(4a−3b)^2$
$(x3 + 5)^2$

Solución

Usando el patrón$(a ± b)^2 = a^2 ± 2ab + b^2$, expandimos cada uno binomialmente mentalmente, anotando la respuesta sin ningún paso intermedio.

$(2y−3)^2 = 4y^2 −12y +9$
$(4a−3b)^2 = 16a^2 −24ab +9b^2$
$(x^3 + 5)^2 = x^6 + 10x^3 + 25$

Ejercicio$\PageIndex{3}$

Ampliar:$(5x^4 −3)^2$

Contestar: $25x^8 −30x^4 +9$

Ahora bien, debido a que el factoring es “no multiplicar”, debería ser un asunto sencillo revertir el proceso de Ejemplo$\PageIndex{3}$.

Ejemplo$\PageIndex{4}$

Factorizar cada uno de los siguientes trinomios:

$4y^2 −12y + 9$
$16a^2 −24ab +9b^2$
$x^6 + 10x^3 + 25$

Solución

Debido al trabajo ya realizado en Ejemplo$\PageIndex{3}$, es una tarea sencilla factorizar cada uno de estos trinomios.

$4y^2 −12y + 9 = (2y−3)^2$
$16a^2 −24ab +9b^2 = (4 a−3b)^2$
$x^6 + 10x^3 + 25 = (x^3 + 5)$

Ejercicio$\PageIndex{4}$

Factor:$25x^8 −30x^4 +9$

Contestar: $(5x^4 −3)^2$

Cada uno de los trinomios en Ejemplo$\PageIndex{4}$ es un ejemplo de trinomio cuadrado perfecto.

Trinomio cuadrado perfecto

Si un trinomio$a^2 +2ab + b^2$ es el cuadrado de un binomio, como en$(a+b)^2$, entonces el trinomio se llama trinomio cuadrado perfecto.

Entonces, ¿cómo se reconoce un trinomio cuadrado perfecto? Si el primer y último término de un trinomio son cuadrados perfectos, entonces debes sospechar que puedes estar tratando con un trinomio cuadrado perfecto. No obstante, también hay que tener el término medio correcto para tener un trinomio cuadrado perfecto.

Tabla$\PageIndex{1}$: Lista de Cuadrados
$n$	$n^2$
\ (n\) ">1	\ (n^2\) ">1
\ (n\) ">2	\ (n^2\) ">4
\ (n\) ">3	\ (n^2\) ">9
\ (n\) ">4	\ (n^2\) ">16
\ (n\) ">5	\ (n^2\) ">25
\ (n\) ">6	\ (n^2\) ">36
\ (n\) ">7	\ (n^2\) ">49
\ (n\) ">8	\ (n^2\) ">64
\ (n\) ">9	\ (n^2\) ">81
\ (n\) ">10	\ (n^2\) ">100
\ (n\) ">11	\ (n^2\) ">121
\ (n\) ">12	\ (n^2\) ">144
\ (n\) ">13	\ (n^2\) ">169
\ (n\) ">14	\ (n^2\) ">196
\ (n\) ">15	\ (n^2\) ">225
\ (n\) ">16	\ (n^2\) ">256
\ (n\) ">17	\ (n^2\) ">289
\ (n\) ">18	\ (n^2\) ">324
\ (n\) ">19	\ (n^2\) ">361
\ (n\) ">20	\ (n^2\) ">400
\ (n\) ">21	\ (n^2\) ">441
\ (n\) ">22	\ (n^2\) ">484
\ (n\) ">23	\ (n^2\) ">529
\ (n\) ">24	\ (n^2\) ">576
\ (n\) ">25	\ (n^2\) ">625

Ejemplo$\PageIndex{5}$

Factorizar cada uno de los siguientes trinomios:

$9x^2 −42x + 49$
$49a^2 + 70ab + 25b^2$
$4x^2 −37x +9$

Solución

Tenga en cuenta que el primer y último término de cada trinomio son cuadrados perfectos.

En el trinomio$9x^2−42x+49$, tenga en cuenta que$(3x)^2 =9x^2$ y$72 = 49$. De ahí que el primer y último término sean cuadrados perfectos. Tomando las raíces cuadradas, sospechamos que$9x^2 −42x + 49$ factores de la siguiente manera:\[9x^2 −42x + 49 \overset{?}{=} (3x−7)^2 \nonumber \] Sin embargo, debemos verificar para ver si el término medio es correcto. Multiplicar$3x$ y$7$, luego doblar:$2(3x)(7) = 42x$. Así, el término medio es correcto y por lo tanto\[9x^2 −42x + 49 = (3x−7)^2\nonumber \]
En el trinomio$49a^2+70ab+25b^2$, tenga en cuenta que$(7a)^2 = 49a^2$ y$(5b)^2 = 25 b^2$. De ahí que el primer y último término sean cuadrados perfectos. Tomando las raíces cuadradas, sospechamos que$49a^2 + 70ab + 25 b^2$ factores de la siguiente manera:\[49a^2 + 70ab + 25 b^2 \overset{?}{=} (7 a +5 b)^2 \nonumber \] Sin embargo, debemos verificar para ver si el término medio es correcto. Multiplicar$7a$ y$5b$, luego doblar:$2(7a)(5b) = 70ab$. Así, el término medio es correcto y por lo tanto\[49a^2 + 70ab + 25 b^2 = (7 a +5 b)^2 \nonumber \]
En el trinomio$4x^2−37x+9$, tenga en cuenta que$(2x)^2 =4x^2$ y$(3)^2 = 9$. De ahí que el primer y último término sean cuadrados perfectos. Tomando las raíces cuadradas, sospechamos que$4x^2 −37x + 9$ factores de la siguiente manera:\[4x^2 −37x +9 \overset{?}{=} (2x−3)^2 \nonumber \]

No obstante, debemos verificar para ver si el término medio es correcto. Multiplicar$2x$ y$3$, luego doblar:$2(2x)(3) = 12x$. Sin embargo, este no es el término medio de$4x^2 −37x + 9$, por lo que esta factorización es incorrecta! Debemos encontrar otra manera de factorizar este trinomio.

Comparando$4x^2 −37x+ 9$ con$ax^2 + bx+ c$, necesitamos un par de enteros cuyo producto es$ac = 36$ y cuya suma es$b = −37$. El par entero$−1$ y$−36$ viene a la mente. Reemplazar el término medio como una suma de términos similares usando este par ordenado.

\[\begin{align*} 4x^2-37x +9 &= 4x^2-x-36x +9 \quad \color {Red} -37x=-x-36x\\ &= x(4x-1)-9(4x-1) \quad \color {Red} \text {Factor by grouping}\\ &= (x-9)(4x-1) \quad \color {Red} \text {Factor out } 4x-1 \end{align*} \nonumber \]

Este ejemplo demuestra claramente lo importante que es verificar el término medio.

Ejercicio$\PageIndex{5}$

Factor:$16x^2 + 72x + 81$

Contestar: $(4x + 9)^2$

¡Recuerda la primera regla del factoraje!

La primera regla de factorización

El primer paso a realizar en cualquier problema de factoring es factorizar el$\mathrm{GCF}$.

Ejemplo$\PageIndex{6}$

Factorizar cada uno de los siguientes trinomios:

$2x^3y + 12x^2y^2 + 18xy^3$
$−4x^5 + 32x^4 −64x^3$

Solución

Recuerde, primer factor fuera del$\mathrm{GCF}$.

En el trinomio$2x^3y + 12x^2y^2 + 18xy^3$, observamos que el$\mathrm{GCF}$ de$2x^3y$,$12x^2y^2$, y$18xy^3$ es$2xy$. Primero factorizamos hacia fuera$2xy$. \[2x^3y + 12x^2y^2 + 18xy^3 =2xy(x^2 +6xy +9y^2) \nonumber \]Ahora notamos que el primer y último término del factor trinomial resultante son cuadrados perfectos, por lo que tomamos sus raíces cuadradas y factores de la siguiente manera. \[=2xy(x +3y)^2 \nonumber \]Por supuesto, la última factorización es correcta sólo si el término medio es correcto. Porque$2(x)(3y)=6xy$ coincide con el término medio de$x^2 +6xy +9y^2$, tenemos un trinomio cuadrado perfecto y nuestro resultado es correcto.
En el trinomio$−4x^5 + 32x^4 −64x^3$, observamos que el$\mathrm{GCF}$ de$4x^5$,$32x^4$, y$64x^3$ es$4x^3$. Primero factorizamos hacia fuera$4x^3$. \[−4x^5 + 32x^4 −64x^3 =4x^3(−x^2 +8x−16) \nonumber \]Sin embargo, el primer y tercer término de$−x^2 +8x−16$ son negativos y, por lo tanto, no son cuadrados perfectos. Empecemos de nuevo, esta vez factorizando$−4x^3$. \[−4x^5 + 32x^4 −64x^3 = −4x^3(x^2 −8x + 16) \nonumber \]Esta vez el primer y tercer término de$x^2−8x+16$ son cuadrados perfectos. Tomamos sus raíces cuadradas y escribimos:\[= −4x^3(x−4)^2 \nonumber \] Nuevamente, esta última factorización es correcta sólo si el término medio es correcto. Porque$2(x)(4) = 8x$, sí tenemos un trinomio cuadrado perfecto y nuestro resultado es correcto.

Ejercicio$\PageIndex{6}$

Factor:$−4x^3 −24x^2 −36x$

Contestar: $−4x(x + 3)^2$

La Diferencia de los Cuadrados

La segunda forma de producto especial que aprendimos en el Capítulo 5 fue la diferencia de cuadrados.

La diferencia de los cuadrados

Aquí está la regla de la diferencia de cuadrados. \[(a + b)(a−b)=a^2 − b^2 \nonumber \]

Si estás multiplicando dos binomios que tienen exactamente los mismos términos en las posiciones “Primera” y los mismos términos exactos en las posiciones “Últimas”, pero un conjunto está separado por un signo más mientras que el otro conjunto está separado por un signo menos, entonces multiplica de la siguiente manera:

Cuadrando el primer término:$a^2$
Cuadrar el segundo término:$b^2$
Coloca un signo menos entre las dos casillas.

Ejemplo$\PageIndex{7}$

Amplíe cada una de las siguientes opciones:

$(3x+5)(3x-5)$
$(a^3 −2b^3)(a^3 +2b^3)$

Solución

Aplicamos la diferencia de patrón de cuadrados para expandir cada uno de los problemas dados.

En$(3x + 5)(3x − 5)$, tenemos exactamente los mismos términos en las posiciones “Primera” y “Última”, con el primer conjunto separado por un signo más y el segundo conjunto separado por un signo menos.
1. Cuadrando el primer término:$(3x)^2 =9x^2$
2. Cuadrar el segundo término:$5^2 = 25$
3. Coloca un signo menos entre las dos casillas.

Por lo tanto:\[(3x + 5)(3x−5) = 9x^2 −25 \nonumber \]

En$(a^3 −2b^3)(a^3 +2b^3)$, tenemos exactamente los mismos términos en las posiciones “Primera” y “Última”, con el primer conjunto separado por un signo menos y el segundo conjunto separado por un signo más.
1. Cuadrando el primer término:$(a^3)^2 = a^6$
2. Cuadrar el segundo término:$(2b^3)^2 =4b^6$
3. Coloca un signo menos entre las dos casillas.

Por lo tanto:\[(a^3 −2b^3)(a^3 +2b^3)=a^6 −4b^6 \nonumber \]

Ejercicio$\PageIndex{7}$

Ampliar:$(4x−3y)(4x +3y)$

Contestar: $16x^2 −9y^2$

Debido a que el factoring es “no multiplicar”, debe ser un asunto sencillo para revertir el proceso de Ejemplo$\PageIndex{7}$.

Ejemplo$\PageIndex{8}$

Factorizar cada uno de los siguientes:

$9x^2 −25$
$a^6 −4b^6$

Solución

Debido al trabajo ya realizado en Ejemplo$\PageIndex{7}$, es una cuestión sencilla factorizar (o “desmultiplicar”) cada uno de estos problemas.

$9x^2 −25 = (3x + 5)(3x−5)$
$a^6 −4b^6 =(a^3 −2b^3)(a^3 +2b^3)$

En cada caso, anote cómo tomamos las raíces cuadradas de cada término, luego separamos un conjunto con un signo más y el otro con un signo menos. Debido a la propiedad conmutativa de la multiplicación, no importa cuál hagas más y cuál hagas menos.

Ejercicio$\PageIndex{8}$

Factor:$81x^2 −49$

Contestar: $(9x + 7)(9x−7)$

Recuerda siempre la primera regla del factoraje.

Ejemplo$\PageIndex{9}$

Factor:$x^3 −9x$

Solución

En$x^3 −9x$, el$\mathrm{GCF}$ de$x^3$ y$9x$ es$x$. Factorizar hacia fuera$x$. \[x^3−9x = x(x^2 −9) \nonumber \]Tenga en cuenta que ahora$x^2−9$ es la diferencia de dos cuadrados perfectos. Tome las raíces cuadradas de$x^2$ y$9$, que son$x$ y$3$, luego separe un conjunto con un signo más y el otro conjunto con un signo menos.
\[= x(x + 3)(x−3) \nonumber \]

Ejercicio$\PageIndex{9}$

Factor:$4x^4−16x^2$

Contestar: $4x^2(x + 2)(x−2)$

Factoring Completamente

A veces, después de una pasada en la factorización, quedan factores que pueden ser factorizados aún más. Debe seguir factorizando en este caso.

Ejemplo$\PageIndex{10}$

Factor:$x^4 −16$

Solución

En$x^4 −16$, tenemos la diferencia de dos cuadrados:$(x^2)^2 = x^4$ y$4^2 = 16$. Primero, tomamos las raíces cuadradas, luego separamos un conjunto con un signo más y el otro conjunto con un signo menos. \[x^4 −16 = (x^2 + 4)(x^2 −4) \nonumber \]Tenga en cuenta que$x^2+4$ es la suma de dos cuadrados y no factoriza más. Sin embargo,$x^2 −4$ es la diferencia de dos cuadrados. Toma las raíces cuadradas,$x$ y$2$, luego separa un conjunto con un signo más y el otro conjunto con un signo menos.
\[=( x^2 + 4)(x + 2)(x−2) \nonumber \]Hecho. No podemos factorizar más.

Ejercicio$\PageIndex{10}$

Factor:$x^4 −81$

Contestar: $(x^2 + 9)(x + 3)(x−3)$

Ecuaciones no lineales revisitadas

Recuerde, si una ecuación es no lineal, el primer paso es hacer que un lado sea igual a cero moviendo todos los términos a un lado de la ecuación. Una vez que haya completado este importante primer paso, factorizar y aplicar la propiedad cero del producto para encontrar las soluciones.

Ejemplo$\PageIndex{11}$

Resolver para$x$:$25x^2 = 169$

Solución

Haga que un lado sea igual a cero, factor, luego aplique la propiedad cero del producto.

\[\begin{align*} 25x^2 &= 169 \quad \color {Red} \text {Original equation.}\\ 25x^2 - 169 &= 0 \quad \color {Red} \text {Subtract 169 from both sides.} \end{align*} \nonumber \]

Tenga en cuenta que tenemos dos cuadrados perfectos separados por un signo menos. Esta es la diferencia del patrón de cuadrados. Toma las raíces cuadradas, haciendo un término más y un término menos.

\[\begin{align*} (5x + 13)(5x-13) &= 0 \quad \color {Red} \text {Use difference of squares to factor.} \end{align*} \nonumber \]

Utilice la propiedad cero del producto para completar la solución, estableciendo cada factor igual a cero y resolviendo las ecuaciones resultantes.

\[\begin{align*} 5x + 13 &= 0 \\ x &= -\dfrac{13}{5} \end{align*} \nonumber\]

\[\begin{align*} 5x - 13 &= 0 \\ x &= \dfrac{13}{5} \end{align*} \nonumber\]

De ahí que las soluciones de$25x^2 = 169$ son$x =−13/5$ y$x = 13 /5$. Animamos a los lectores a revisar cada una de estas soluciones.

Ejercicio$\PageIndex{11}$

Resolver para$x$:$16x^2 = 121$

Contestar: $−11/4$,$11/4$

Ejemplo$\PageIndex{12}$

Resolver para$x$:$49x^2 + 81 = 126x$

Solución

Haga que un lado sea igual a cero, factor, luego aplique la propiedad cero del producto.

\[\begin{align*} 49x^2+81x &= 126x \quad \color {Red} \text {Original equation.}\\ 49x^2-126x+81 &= 0 \quad \color {Red} \text {Subtract 126x from both sides.} \end{align*} \nonumber \]

Obsérvese que el primer y último término del trinomio son cuadrados perfectos. De ahí que tenga sentido tratar de factorizar como un trinomio cuadrado perfecto, tomando las raíces cuadradas del primer y último término.

\[\begin{align*} (7x-9)^2 &= 0 \quad \color {Red} \text {Factor as a perfect square trinomial.} \end{align*} \nonumber \]

Por supuesto, asegúrate de revisar el término medio. Porque$−2(7x)(9) = −126x$, el término medio es correcto. Porque$(7x−9)^2 = (7 x−9)(7x−9)$, podemos usar la propiedad cero del producto para establecer cada factor igual a cero y resolver las ecuaciones resultantes.

\[\begin{align*} 7x-9 &= 0 \\ x &= \dfrac{9}{7} \end{align*} \nonumber\]

De ahí que la única solución de$49x^2 +81 = 126x$ es$x =9 /7$. Animamos a los lectores a verificar esta solución.

Nota

También se puede argumentar que el único número cuyo cuadrado es cero es el número cero. De ahí, uno puede ir directamente de$(7x−9)^2 =0$ a$7x−9=0$. De ahí que la única solución de$49x^2 + 81 = 126x$ es$x =9 /7$.

Ejercicio$\PageIndex{12}$

Resolver para$x$:$25x^2 = 80x−64$

Contestar: $8/5$

Ejemplo$\PageIndex{13}$

Resolver para$x$:$2x^3 +3x^2 = 50x + 75$

Solución

Haga que un lado sea igual a cero, factor, luego aplique la propiedad cero del producto.

\[\begin{align*} 2x^3 +3x^2 &= 50x + 75 \quad \color {Red} \text {Original equation.}\\ 2x^3 + 3x^2 - 50x - 75 &= 0 \quad \color {Red} \text {Make one side zero.} \end{align*} \nonumber \]

Esta es una expresión de cuatro términos, por lo que intentamos factorizar por agrupación. Factor$x^2$ de los dos primeros términos, y$−25$ de los dos segundos términos.

\[\begin{align*} x^2(2x + 3)-25(2x + 3) &= 0 \quad \color {Red} \text {Factor by grouping}\\ (x^2-25)(2x + 3) &= 0 \quad \color {Red} \text {Factor out } 2x+3 \end{align*} \nonumber\]

Completar la factorización usando la diferencia de cuadrados a factorizar$x^2−25$.

\[\begin{align*} (x+5)(x-5)(2x+3) &= 0 \quad \color {Red} \text {Use difference of squares to factor.} \end{align*} \nonumber \]

Por último, utilice la propiedad cero del producto. Establezca cada factor igual a cero y resuelva para$x$.

\[\begin{align*} x+5 &= 0 \\ x &= -5 \end{align*} \nonumber\]

\[\begin{align*} x-5 &= 0 \\ x &= 5 \end{align*} \nonumber\]

\[\begin{align*} 2x+3 &= 0 \\ x &= -\dfrac{3}{2} \end{align*} \nonumber\]

De ahí que las soluciones de$2x^3 +3x^2 = 50x+75$ son$x = −5$,$x = 5$, y$x = −3/2$. Animamos a los lectores a revisar cada una de estas soluciones.

Ejercicio$\PageIndex{13}$

Resolver para$x$:$5x^3 + 36 =x^2 + 180x$

Contestar: $−6$,$6$,$1/5$

Resolvamos otra ecuación no lineal, coincidiendo con las soluciones algebraicas y gráficas.

Ejemplo$\PageIndex{14}$

Resuelve la ecuación$x^3 =4x$, tanto algebraica como gráficamente, luego compara tus respuestas.

Solución

Tenga en cuenta que tenemos una potencia$x$ mayor a uno, por lo que la ecuación$x^3 =4x$ es no lineal. Hacer un lado cero y factorizar.

\[\begin{align*} x^3 &= 4x \quad \color {Red} \text {Original equation.}\\ x^3-4x &= 0 \quad \color {Red} \text {Nonlinear. Make one side zero. }\\ x(x^2-4) &=0 \quad \color {Red} \text {Factor out GCF.}\\ x(x+2)(x-2) &= 0 \quad \color {Red} \text {Apply difference of squares.} \end{align*} \nonumber\]

Tenga en cuenta que ahora tenemos un producto de tres factores que equivale a cero. La propiedad cero del producto dice que al menos uno de estos factores debe ser igual a cero.

\[\begin{align*} x &= 0 \end{align*} \nonumber\]

\[\begin{align*} x+2 &= 0 \\ x &= -2 \end{align*} \nonumber\]

\[\begin{align*} x-2 &= 0 \\ x &= 2 \end{align*} \nonumber\]

De ahí que las soluciones de$x^3 =4x$ son$x = 0$,$x = −2$, y$x = 2$.

Solución gráfica

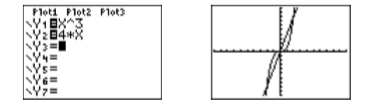
Carga$y = x^3$ y$y =4x$ en$\mathbb{Y1}$ y$\mathbb{Y2 }$ en el menú Y= de tu calculadora. Seleccione 6:ZStandard en el menú ZOOM para producir la gráfica en la Figura$\PageIndex{1}$.

Aunque la imagen de la Figura$\PageIndex{1}$ muestra los tres puntos de intersección, ajustando los parámetros VENTANA como se muestra en la Figura$\PageIndex{2}$, luego presionar el botón GRAPADO producirá una vista más agradable de los puntos de intersección, como se muestra en la figura a la derecha en las Figuras $\PageIndex{2}$.

higo 6.5.1.png — Figura$\PageIndex{1}$: Croquizado$y = x^3$ y$y =4x$.

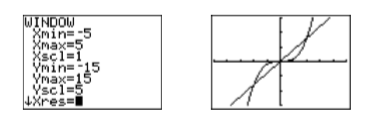
higo 6.5.2.png — Figura$\PageIndex{2}$: Ajuste de la ventana de visualización.

Utilice la herramienta 5:intersectar del menú CALC para encontrar los tres puntos de intersección. Presione la tecla INTRO en respuesta a “Primera curva”, luego presione ENTRAR nuevamente en respuesta a “Segunda curva”, luego use la tecla de flecha izquierda para mover el cursor cerca del punto de intersección más a la izquierda y presione ENTRAR en respuesta a “Adivina”. El resultado se muestra en la primera imagen de la izquierda en la Figura$\PageIndex{3}$. Repita el proceso para encontrar los puntos restantes de intersección. Los resultados se muestran en las dos últimas imágenes de la Figura$\PageIndex{3}$.

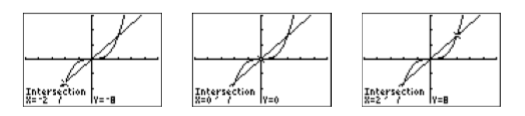
higo 6.5.3.png — Figura$\PageIndex{3}$: Encontrar los puntos de intersección.

Así, las soluciones gráficas son$x =−2$$x = 0$, y$x = 2$.

Reportando la solución en tu tarea:

Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{4}$).
Coloca tus parámetros de VENTANA al final de cada eje (ver Figura$\PageIndex{4}$).
Etiquete la gráfica con su ecuación (ver Figura$\PageIndex{4}$).
Deja caer líneas verticales discontinuas a través$x$ de cada intersección. Sombra y etiquete los$x$ valores -de los puntos donde la línea vertical discontinua cruza el$x$ eje. Estas son las soluciones de la ecuación$x^3 = 4x$ (ver Figura$\PageIndex{4}$).

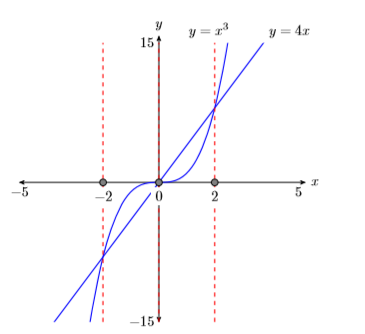
higo 6.5.4.png — Figura$\PageIndex{4}$: Reportando tu solución gráfica en tu tarea.

Por último, tenga en cuenta que las soluciones gráficas$x = −2$$x = 0$,, y$x = 2$ coinciden con nuestras soluciones algebraicas exactamente.

Ejercicio$\PageIndex{14}$

Resuelve la ecuación$x^3 = 16x$ tanto algebraica como gráficamente, luego compara tus respuestas.

Contestar

$−4$,$0$,$4$

$Ejercicio 6.5.14.png$