8.1: Introducción a la notación radical

Última actualización
Guardar como PDF

Page ID: 111654

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Sabemos cuadrar un número. Por ejemplo:

$5^2 = 25$
$(−5)^2 = 25$

Tomar la raíz cuadrada de un número es lo opuesto a la cuadratura.

La raíz cuadrada no negativa de$25$ es$5$.
La raíz cuadrada negativa de$25$ es$−5$.

Así, al buscar una raíz cuadrada de un número, estamos buscando un número cuyo cuadrado sea igual a nuestro número.

Ejemplo$\PageIndex{1}$

Encuentra las raíces cuadradas de$81$.

Solución

Estamos buscando un número cuya plaza es$81$.

Porque$9^2 = 81$, la raíz cuadrada no negativa de$81$ es$9$.
Porque$(−9)^2 = 81$, la raíz cuadrada negativa de$81$ es$−9$.

De ahí,$81$ tiene dos raíces cuadradas,$−9$ y$9$.

Ejercicio$\PageIndex{1}$

Encuentra las raíces cuadradas de$64$.

Responder: $8$y$−8$

Ejemplo$\PageIndex{2}$

Encuentra las raíces cuadradas de$0$.

Solución

Estamos buscando un número cuya plaza es$0$.

Porque$0^2 = 0$, la raíz cuadrada no negativa de$0$ es$0$.

Ningún otro número al cuadrado será igual a cero. De ahí que el cero tenga exactamente una raíz cuadrada, es decir, cero.

Ejercicio$\PageIndex{2}$

Encuentra las raíces cuadradas de$100$.

Responder: $10$y$−10$

Ejemplo$\PageIndex{3}$

Encuentra las raíces cuadradas de$−36$.

Solución

Estamos buscando un número cuya plaza es$−36$. No obstante, cada vez que cuadras un número real, el resultado nunca es negativo. De ahí$−36$ que no tenga raíces cuadradas reales. ¹

Ejercicio$\PageIndex{3}$

Encuentra las raíces cuadradas de$−25$.

Responder: sin raíces cuadradas reales

Las introducciones en Ejemplos$\PageIndex{1}$$\PageIndex{2}$,, y$\PageIndex{3}$ conducen a la siguiente definición.

Desafiando las Raíces Cuadradas de un Número

Las soluciones de$x^2 = a$ se llaman raíces cuadradas de$a$.

Caso:$a>0$. La ecuación$x^2 = a$ tiene dos soluciones reales, a saber$x =\pm \sqrt{a}$.

La notación$\sqrt{a}$ llama a la raíz cuadrada no egativa.
La notación$−\sqrt{a}$ llama a la raíz cuadrada negativa.

Caso:$a = 0$. La ecuación$x^2 = 0$ tiene exactamente una solución, a saber$x = 0$.

Caso:$a<0$. La ecuación no$x^2 = a$ tiene soluciones reales.

Ejemplo$\PageIndex{4}$

Resuelva$x^2 = 9$ para$x$, luego simplifique sus respuestas.

Solución

Debido a que el lado derecho de$x^2 = 9$ es positivo, la ecuación tiene dos soluciones.

\[\begin{align*} x^2 &= 9 \quad \color {Red} \text {Original equation.}\\ x &= \pm \sqrt{9} \quad \color {Red} \text {Two answers: } -\sqrt{9} \text { and } \sqrt{9} \end{align*} \nonumber\]

Para simplificar estas respuestas, necesitamos entender los siguientes hechos:

$\sqrt{9}$pide la raíz cuadrada no negativa de$9$. Porque$(3)^2 = 9$, la raíz cuadrada no negativa de$9$ es$3$. De ahí,$\sqrt{9} = 3$.
$-\sqrt{9}$pide la raíz cuadrada negativa de$9$. Porque$(−3)^2 = 9$, la raíz cuadrada negativa de$9$ es$−3$. De ahí,$-\sqrt{9}=−3$.

Así, las soluciones de$x^2 = 9$ son$x = \pm 3$, lo que equivale a decir “$x =−3$o”$x = 3$.

Ejercicio$\PageIndex{4}$

Resuelva$x^2 = 16$ para$x$, luego simplifique sus respuestas.

Responder: $4$,$-4$

Ejemplo$\PageIndex{5}$

Resuelva$x^2 = 0$ para$x$, luego simplifique la respuesta.

Solución

Sólo hay un número cuyo cuadrado es igual$0$, a saber$0$.

\[\begin{align*} x^2 &= 0 \quad \color {Red} \text {Original equation.}\\ x &= 0 \quad \color {Red} \text {One answer: } (0)^2 = 0. \end{align*} \nonumber\]

Así, la única solución de$x^2 = 0$ es$x = 0$. En consecuencia, la raíz cuadrada no negativa de cero es cero. De ahí,$\sqrt{0} = 0$.

Ejercicio$\PageIndex{5}$

Resuelva$x^2 = 49$ para$x$, luego simplifique las respuestas.

Responder: $7$,$-7$

Ejemplo$\PageIndex{6}$

Resuelva$x^2 =−4$ para$x$, luego simplifique la respuesta.

Solución

No se puede cuadrar un número real y obtener un resultado negativo. De ahí$x^2 = −4$ que no tenga soluciones reales. Por lo tanto, no$\sqrt{-4}$ es un número real.

Ejercicio$\PageIndex{6}$

Resuelva$x^2 = −9$ para$x$, luego simplifique las respuestas.

Responder: no hay soluciones reales

Ejemplo$\PageIndex{7}$

Simplifica cada uno de los siguientes:

$\sqrt{121}$
-$\sqrt{225}$
$\sqrt{-100}$
-$\sqrt{324}$

Solución

Recuerde, la notación$\sqrt{a}$ exige la raíz cuadrada no negativa de$a$, mientras que la notación -$\sqrt{a}$ pide la raíz cuadrada negativa de$a$.

Porque$11^2 = 121$, la raíz cuadrada no negativa de$225$ es$-15$. Así:\[-\sqrt{225} = -15 \nonumber \]
Porque$(-15)^2 = 225$, la raíz cuadrada no negativa de$121$ es$11$. Así:\[\sqrt{121} = 11 \nonumber \]
No se puede cuadrar un número real y obtener$−100$. Por lo tanto, no$\sqrt{-100}$ es un número real.
Porque$(-18)^2 = 324$, la raíz cuadrada no negativa de$324$ es$-18$. Así:\[-\sqrt{324} = -18 \nonumber \]

Ejercicio$\PageIndex{7}$

Simplificar:$−\sqrt{144}$

Responder: $-12$

Cuadrando “deshace” tomando la raíz cuadrada.

Cuadrado de raíces cuadradas

Si$a>0$, entonces ambos$-\sqrt{a}$ y$\sqrt{a}$ son soluciones de$x^2 = a$. En consecuencia, si sustituimos cada uno de ellos en la ecuación$x^2 = a$, obtenemos:

$(-\sqrt{a})^2 = a$y$(\sqrt{a})^2 = a$

Ejemplo$\PageIndex{8}$

Simplifica cada una de las siguientes expresiones:

$(\sqrt{5})^2$
$(-\sqrt{7})^2$
$(\sqrt{-11})^2$

Solución

Nos encargaremos de cada caso con cuidado.

Porque$\sqrt{5}$ es una solución de$x^2 = 5$, si nos cuadramos$\sqrt{5}$, deberíamos conseguir$5$. \[(\sqrt{5})^2 =5 \nonumber \]
Porque$-\sqrt{7}$ es una solución de$x^2 = 7$, si nos cuadramos$-\sqrt{7}$, deberíamos conseguir$7$. \[(-\sqrt{7})^2 =7 \nonumber \]
Porque no$x^2 = −11$ tiene respuestas reales, no$\sqrt{-11}$ es un número real. Cursos avanzados como álgebra universitaria o trigonometría introducirán el complejo sistema numérico y mostrarán cómo manejar esta expresión.

Ejercicio$\PageIndex{8}$

Simplificar:$(−\sqrt{21})^2$

Responder: $21$

Uso de la Calculadora Gráfica

Hasta este punto, la ecuación$x^2 = a$ ha implicado cuadrados perfectos. Por ejemplo, si empezamos con$x^2 = 25$, entonces las soluciones son$x = \pm \sqrt {25}$. Porque$25$ es una plaza perfecta, podemos simplificar aún más, llegando a$x =\pm 5$.

Sin embargo, el lado derecho de$x^2 = a$ no tiene que ser un cuadrado perfecto. Por ejemplo, la ecuación$x^2 = 7$ tiene dos soluciones reales,$x =\pm \sqrt {7}$. Porque no$7$ es un cuadrado perfecto, no podemos simplificar más. En el siguiente ejemplo, usaremos la calculadora gráfica para comparar esta solución algebraica con una solución gráfica y ojalá brindemos alguna garantía de que$−\sqrt{7}$ y$\sqrt {7}$ sean soluciones perfectamente válidas de$x^2 = 7$.

Ejemplo$\PageIndex{9}$

Utilice la calculadora gráfica para resolver$x^2 = 7$. Entonces resuelve la ecuación algebraicamente y compara las respuestas.

Solución

Ingrese cada lado de la ecuación$x^2 = 7$ en el menú Y= (ver Figura$\PageIndex{1}$), luego seleccione 6:ZEstándar para producir la imagen en la Figura$\PageIndex{1}$.

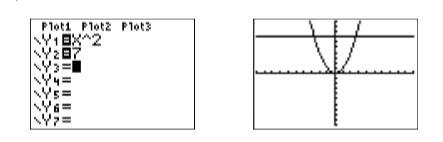
higo 8.1.1.png — Figura$\PageIndex{1}$: Esbozar cada lado de$x^2 = 7$.

Utilice la utilidad 5:intersectar en el menú CALC para encontrar los puntos de intersección. Presione ENTRAR en respuesta a “Primera curva”, presione ENTRAR en respuesta a “Segunda curva”, luego use las teclas de flecha para mover el cursor más cerca del punto de intersección a la izquierda que al de la derecha. Presiona ENTRAR en respuesta a “Adivina”. Esto producirá el punto de intersección que se muestra en la imagen de la izquierda en la Figura$\PageIndex{2}$. Repita el procedimiento para encontrar el punto de intersección en la imagen de la derecha en la Figura$\PageIndex{2}$.

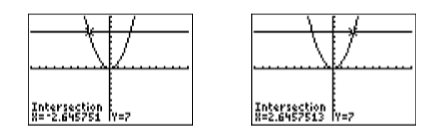
higo 8.1.2.png — Figura$\PageIndex{2}$: Encontrar puntos de intersección.

Las soluciones aproximadas de$x^2 = 7$ son$x≈− 2.645751$ y$x ≈2.6457513$.

Reportando la solución en tu tarea: Duplica la imagen en la ventana de visualización de tu calculadora en tu página de tareas. Usa una regla para dibujar todas las líneas, pero a mano alzada cualquier curva.

Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{3}$).
Coloca tus parámetros WINDOW al final de cada eje (ver Figura$\PageIndex{3}$).
Etiquetar cada gráfica con su ecuación (ver Figura$\PageIndex{3}$).
Coloca líneas verticales discontinuas a través de cada punto de intersección. Sombra y etiquete los valores x de los puntos donde la línea vertical discontinua cruza el eje x. Estas son las soluciones de la ecuación$x^2 = 7$ (ver Figura$\PageIndex{3}$).

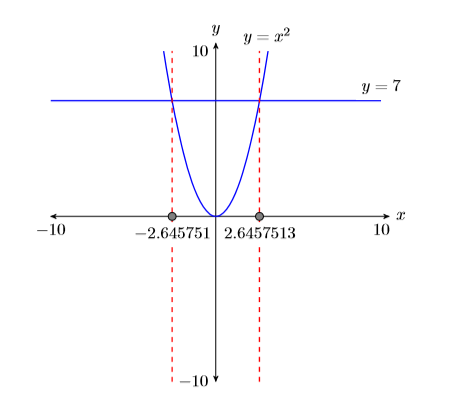
higo 8.1.3.png — Figura$\PageIndex{3}$: Reportando tu solución gráfica en tu tarea.

Ahora resolvemos la ecuación algebraicamente.

\[\begin{align*} x^2 &= 7 \\ x &= \pm \sqrt{7} \end{align*} \nonumber\]

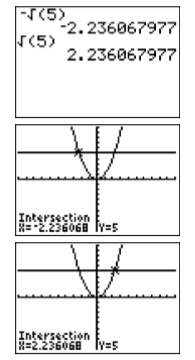
En este punto, la pregunta es: “¿Estas soluciones algebraicas coinciden con las soluciones gráficas de la Figura$\PageIndex{3}$?” Usemos nuestra calculadora para comparar resultados. Localice el símbolo de raíz cuadrada$\sqrt{ }$ en la caja de la calculadora encima de la$x^2$ tecla en la columna más a la izquierda en el teclado de la calculadora. Tenga en cuenta que tendremos que usar la$2^{nd}$ clave para acceder a este operador. Ingrese$-\sqrt{(7)}$ y presione ENTRAR. Luego ingrese$\sqrt{(7)}$ y presione ENTRAR. Los resultados se muestran en la Figura$\PageIndex{4}$.

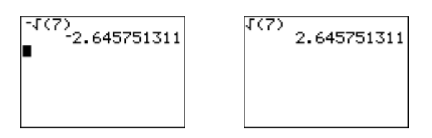
higo 8.1.4.png — Figura$\PageIndex{4}$: Computación$-\sqrt{7}$ y$\sqrt{7}$.

Así,$-\sqrt{7} ≈− 2.645751311$ y$\sqrt{7} ≈ 2.645751311$. Observe cómo estos coinciden estrechamente con las aproximaciones gráficas en la Figura$\PageIndex{3}$.

Ejercicio$\PageIndex{9}$

Resuelve la ecuación$x^2 =5$ tanto algebraica como gráficamente, luego compara tus respuestas.

Responder

$-\sqrt{5}$,$\sqrt{5}$

$Ex 8.1.9.png$

Ejemplo$\PageIndex{10}$

Utilice la calculadora gráfica para resolver$x^2 = −5$. Entonces resuelve la ecuación algebraicamente y compara las respuestas.

Solución

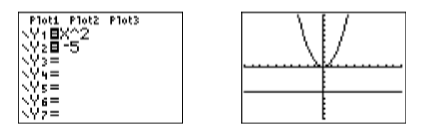
Ingrese cada lado de la ecuación$x^2 = −5$ en el menú Y= (ver Figura$\PageIndex{5}$), luego seleccione 6:ZEstándar para producir la imagen en la Figura$\PageIndex{5}$.

higo 8.1.5.png — Figura$\PageIndex{5}$: Esbozar cada lado de$x^2 = −5$.

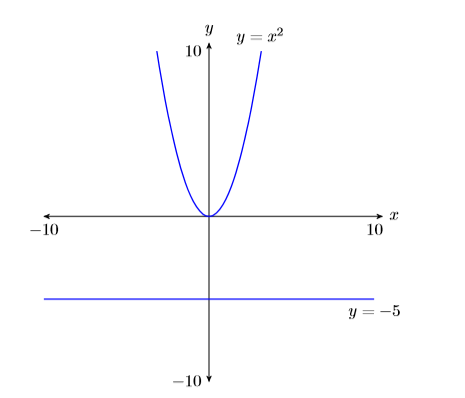
Etiquete los ejes horizontal y vertical con$x$ y$y$, respectivamente (ver Figura$\PageIndex{6}$).
Coloca tus parámetros de VENTANA al final de cada eje (ver Figura$\PageIndex{6}$).
Etiquetar cada gráfica con su ecuación (ver Figura$\PageIndex{6}$).

Debido a que no hay puntos de intersección, la gráfica de la Figura nos$\PageIndex{6}$ informa que la ecuación no$x^2 = −5$ tiene soluciones reales. Ahora resolvemos la ecuación algebraicamente. $x^2 = −5$Sin embargo, no se puede cuadrar un número real y obtener una respuesta negativa. De ahí que la ecuación no$x^2 = −5$ tenga soluciones reales. Esto concuerda completamente con la gráfica de la Figura$\PageIndex{6}$.

higo 8.1.6.png — Figura$\PageIndex{6}$: Reportando tu solución gráfica en tu tarea.

Aproximación a las raíces cuadradas

Tabla$\PageIndex{1}$: Lista de Cuadrados
$n$	$n^2$
\ (n\) ">0	\ (n^2\) ">0
\ (n\) ">1	\ (n^2\) ">1
\ (n\) ">2	\ (n^2\) ">4
\ (n\) ">3	\ (n^2\) ">9
\ (n\) ">4	\ (n^2\) ">16
\ (n\) ">5	\ (n^2\) ">25
\ (n\) ">6	\ (n^2\) ">36
\ (n\) ">7	\ (n^2\) ">49
\ (n\) ">8	\ (n^2\) ">64
\ (n\) ">9	\ (n^2\) ">81
\ (n\) ">10	\ (n^2\) ">100
\ (n\) ">11	\ (n^2\) ">121
\ (n\) ">12	\ (n^2\) ">144
\ (n\) ">13	\ (n^2\) ">169
\ (n\) ">14	\ (n^2\) ">196
\ (n\) ">15	\ (n^2\) ">225
\ (n\) ">16	\ (n^2\) ">256
\ (n\) ">17	\ (n^2\) ">289
\ (n\) ">18	\ (n^2\) ">324
\ (n\) ">19	\ (n^2\) ">361
\ (n\) ">20	\ (n^2\) ">400
\ (n\) ">21	\ (n^2\) ">441
\ (n\) ">22	\ (n^2\) ">484
\ (n\) ">23	\ (n^2\) ">529
\ (n\) ">24	\ (n^2\) ">576
\ (n\) ">25	\ (n^2\) ">625

Los cuadrados en la “Lista de Cuadrados” que se muestran en Tabla se$\PageIndex{1}$ denominan cuadrados perfectos. Cada uno es el cuadrado de un número entero. Pero no todos los números son cuadrados perfectos. Por ejemplo, en el caso de$\sqrt{24}$, no hay un número entero cuyo cuadrado sea igual a$24$. No obstante, esto no$\sqrt{24}$ impide ser un número perfectamente bueno.

Podemos usar la “Lista de Cuadrados” para encontrar aproximaciones decimales cuando el radicando no es un cuadrado perfecto.

Ejemplo$\PageIndex{11}$

Estimar$\sqrt{24}$ adivinando. Usa una calculadora para encontrar un resultado más preciso y compara este resultado con tu suposición.

Solución

De la “Lista de Cuadrados”, señalar que$24$ se encuentra entre$16$ y$25$, así$\sqrt{24}$ estará entre$4$ y$5$, con$\sqrt{24}$ mucho más cerca$5$ de lo que está a$4$.

$Ejemplo 8.1.11.png$

Vamos a adivinar\[\sqrt{24}≈ 4.8\nonumber \]. Como cheque, vamos a cuadrar ¡\[4.8. (4.8)^2 = (4 .8)(4.8) = 23.04 \nonumber \]No del todo$24$! Claramente,$\sqrt{24}$ debe ser un poco más grande que$4.8$.

Usemos una calculadora científica para obtener una mejor aproximación. De nuestra calculadora, usando el botón de raíz cuadrada, encontramos\[\sqrt{24}≈ 4.89897948557 \nonumber \].

A pesar de que esto es mejor que nuestra estimación de$4.8$, sigue siendo sólo una aproximación. Nuestra calculadora solo era capaz de proporcionar$11$ cifras decimales. Sin embargo, la representación decimal exacta de$\sqrt{24}$ es un decimal inﬁnita que nunca termina y nunca establece un patrón de repetición.

Solo por diversión, aquí hay una aproximación decimal de$\sqrt{24}$ que es precisa a los$1000$ lugares, cortesía de www.wolframalpha.com

$Ejemplo 8.1.11a.png$

Si multiplicaras este número por sí mismo (cuadrar el número), obtendrías un número que está muy cerca$24$, pero no sería exactamente$24$. Todavía habría un poco de discrepancia.

Ejercicio$\PageIndex{11}$

Estimación:$\sqrt{83}$

Responder: $9.1$

Referencia

1 Cuando decimos que no$−36$ tiene raíces cuadradas reales, queremos decir que no hay números reales que sean raíces cuadradas de$−36$. La razón por la que enfatizamos la palabra real en esta situación es el hecho de que$−36$ sí tiene dos raíces cuadradas que son elementos de los números complejos, un conjunto de números que suelen introducirse en cursos avanzados como álgebra universitaria o trigonometría.