8.2: Simplificar expresiones radicales

Última actualización
Guardar como PDF

Page ID: 111649

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Comencemos comparando dos expresiones matemáticas.

\[\begin{align*} \sqrt{9}\sqrt{16} &= 3\cdot 4 \\ &= 12 \end{align*} \nonumber \]

\[\begin{align*} \sqrt{9\cdot 16} &= \sqrt{144} \\ &= 12 \end{align*} \nonumber\]

Tenga en cuenta que ambos$\sqrt{9}\sqrt{16}$ e$\sqrt{9\cdot 16}$ iguales$12$. De ahí,$\sqrt{9}\sqrt{16} = \sqrt{9\cdot 16}$. Veamos otro ejemplo.

\[\begin{align*} \sqrt{4}\sqrt{9} &= 2\cdot 3 \\ &= 6 \end{align*} \nonumber \]

\[\begin{align*} \sqrt{4\cdot 9} &= \sqrt{36} \\ &= 6 \end{align*} \nonumber\]

Tenga en cuenta que ambos$\sqrt{4}\sqrt{9}$ e$\sqrt{4\cdot 9}$ iguales$6$. De ahí,$\sqrt{4}\sqrt{9} = \sqrt{4\cdot 9}$. Parece que se está formando un patrón, a saber:

\[\sqrt{a}\sqrt{b} = \sqrt{ab} \nonumber \]

Probemos un ejemplo en nuestra calculadora. Primero ingrese$\sqrt{2}\sqrt{3}$, luego ingrese$\sqrt{2\cdot 3}$ (ver Figura$\PageIndex{1}$). Tenga en cuenta que producen el mismo resultado. Por lo tanto,$\sqrt{2}\sqrt{3} = \sqrt{2\cdot 3}$

higo 8.2.1.png — Figura$\PageIndex{1}$: Tenga en cuenta que$\sqrt{2}\sqrt{3} = \sqrt{2\cdot 3}$

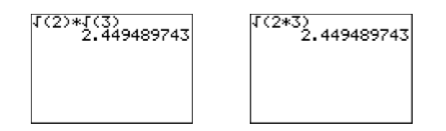
La discusión anterior nos lleva al siguiente resultado.

Propiedad de multiplicación de radicales

Si$a ≥ 0$ y$b ≥ 0$, entonces:\[\sqrt{a}\sqrt{b} = \sqrt{a\cdot b} \nonumber \]

Ejemplo$\PageIndex{1}$

Simplifique cada una de las siguientes expresiones tanto como sea posible:

$\sqrt{3} \sqrt{11}$
$\sqrt{12} \sqrt{3}$
$\sqrt{2} \sqrt{13}$

Solución

En cada caso, use la propiedad$\sqrt{a} \sqrt{b}=\sqrt{a b}$. Es decir, multiplique los dos números bajo el signo de raíz cuadrada, colocando el producto bajo una sola raíz cuadrada.

$\begin{aligned} \sqrt{3} \sqrt{11} &=\sqrt{3 \cdot 11} \\ &=\sqrt{33} \end{aligned}$
$\begin{aligned} \sqrt{12} \sqrt{3} &=\sqrt{12 \cdot 3} \\ &=\sqrt{36} \\ &=6 \end{aligned}$
$\begin{aligned} \sqrt{2} \sqrt{13} &=\sqrt{2 \cdot 13} \\ &=\sqrt{26} \end{aligned}$

Ejercicio$\PageIndex{1}$

Simplificar:$\sqrt{2} \sqrt{8}$

Contestar: $4$

Forma Radical Simple

También podemos usar la propiedad a$\sqrt{a} \sqrt{b}=\sqrt{a b}$ la inversa para factorizar un cuadrado perfecto. Por ejemplo:

\[\begin{array}{rlrl}{\sqrt{50}} & {=\sqrt{25} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=5 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{25}=5}\end{array} \nonumber \]

Se dice que la expresión$5\sqrt{2}$ está en forma radical simple. Como reducir una fracción a términos más bajos, siempre debes buscar factorizar un cuadrado perfecto cuando sea posible.

Forma Radical Simple

Si es posible, siempre factifique un cuadrado perfecto.

Ejemplo$\PageIndex{2}$

Colocar$\sqrt{8}$ en forma radical simple.

Solución

De$\sqrt{8}$, podemos factorizar un cuadrado perfecto, en este caso$\sqrt{4}$.

\[\begin{array}{rlrl}{\sqrt{8}} & {=\sqrt{4} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=2 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{4}=2}\end{array} \nonumber \]

Ejercicio$\PageIndex{2}$

Colocar$\sqrt{12}$ en forma radical simple.

Contestar: $2\sqrt{3}$

A veces, después de factorizar un cuadrado perfecto, aún puedes factorizar otro cuadrado perfecto.

Ejemplo$\PageIndex{3}$

Colocar$\sqrt{72}$ en forma radical simple.

Solución

De$\sqrt{72}$, podemos factorizar un cuadrado perfecto, en este caso$\sqrt{9}$.

\[\begin{array}{rlrl}{\sqrt{72}} & {=\sqrt{9} \sqrt{8}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=3 \sqrt{8}} & {} & \color {Red} {\text { Simplify: } \sqrt{9}=3}\end{array} \nonumber \]

No obstante, a partir de$\sqrt{8}$ podemos factorizar otro cuadrado perfecto, en este caso$\sqrt{4}$.

\[\begin{array}{ll}{=3 \sqrt{4} \sqrt{2}} & \color {Red} {\text { Factor out another perfect square. }} \\ {=3 \cdot 2 \cdot \sqrt{2}} & \color {Red} {\text { Simplify: } \sqrt{4}=2} \\ {=6 \sqrt{2}} & \color {Red} {\text { Multiply: } 3 \cdot 2=6}\end{array} \nonumber \]

Solución alternativa

Podemos simplificar el proceso al señalar que podemos$\sqrt{72}$ factorizar$\sqrt{36}$ desde el inicio del proceso.

\[\begin{array}{rlrl}{\sqrt{72}} & {=\sqrt{36} \sqrt{2}} & {} & \color {Red} {\text { Factor out a perfect square. }} \\ {} & {=6 \sqrt{2}} & {} & \color {Red} {\text { Simplify: } \sqrt{36}=6}\end{array} \nonumber \]

Aunque la segunda solución es más eficiente, la primera solución sigue siendo matemáticamente correcta. El punto a hacer aquí es que debemos seguir factorizando un cuadrado perfecto siempre que sea posible. Nuestra respuesta no está en forma simple radical hasta que ya no podamos factorizar un cuadrado perfecto.

Ejercicio$\PageIndex{3}$

Colocar$\sqrt{200}$ en forma radical simple.

Contestar: $10\sqrt{2}$

El teorema de Pitágoras

Un ángulo que mide$90$ grados se llama ángulo recto. Si uno de los ángulos de un triángulo es un ángulo recto, entonces el triángulo se llama triángulo rectángulo. Es tradicional marcar el ángulo recto con un pequeño cuadrado (ver Figura$\PageIndex{2}$).

higo 8.2.2.png — Figura$\PageIndex{2}$:$\triangle A B C$ El triángulo recto tiene un ángulo recto en el vértice$C$.

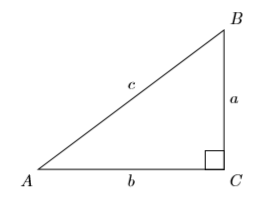
Terminología del triángulo rectángulo

El lado más largo del triángulo rectángulo, el lado directamente opuesto al ángulo recto, se llama hipotenusa del triángulo rectángulo.
Los dos lados restantes del triángulo rectángulo se llaman las patas del triángulo rectángulo.

Prueba del Teorema de Pitágoras

Cada lado del cuadrado de la Figura se$\PageIndex{3}$ ha dividido en dos segmentos, uno de longitud$a$ y otro de longitud$b$.

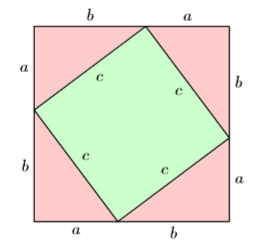
higo 8.2.3.png — Figura$\PageIndex{3}$: Demostrando el Teorema de Pitágoras.

Podemos encontrar el área total de la plaza al cuadrar cualquiera de los lados de la plaza.

\[\begin{array}{ll}{A=(a+b)^{2}} & \color {Red} {\text { Square a side to find area. }} \\ {A=a^{2}+2 a b+b^{2}} & \color {Red} {\text { Squaring a binomial pattern. }}\end{array} \nonumber\]

Así, el área total de la plaza es$A = a^2 +2ab + b^2$.

Un segundo enfoque para determinar el área del cuadrado es sumar las áreas de las partes geométricas que componen el cuadrado. Tenemos cuatro triángulos rectos congruentes, sombreados en rojo claro, con base$a$ y altura$b$. El área de cada uno de estos triángulos se encuentra tomando media veces la base por la altura; es decir, el área de cada triángulos es$(1 / 2) a b$. En el interior, tenemos un cuadrado más pequeño con lateral$c$. Su área se encuentra al cuadrar su lado; es decir, el área del cuadrado más pequeño es$c^2$.

El área total del cuadrado es la suma de sus partes, un cuadrado más pequeño y cuatro triángulos congruentes. Es decir:

\[\begin{array}{ll}{A=c^{2}+4\left(\frac{1}{2} a b\right)} & \color {Red} {\text { Adding the area of the interior square and the area of four right triangles. }} \\ {A=c^{2}+2 a b} & \color {Red} {\text { Simplify: } 4((1 / 2) a b)=2 a b}\end{array} \nonumber \]

Las dos expresiones,$a^2 +2ab+ b^2$ y$c^2 +2ab$, ambas representan el área total del cuadrado grande. De ahí que deben ser iguales entre sí.

\[\begin{aligned} a^{2}+2 a b+b^{2}=c^{2}+2 a b & \quad \color {Red} \text { Each side of this equation represents the area of the large square. } \\ a^{2}+b^{2}=c^{2} & \quad \color {Red} \text { Subtract } 2 a b \text { from both sides. } \end{aligned} \nonumber \]

La última ecuación,$a^2 + b^2 = c^2$, se llama Teorema de Pitágoras.

El teorema de Pitágoras

Si$a$ y$b$ son las patas de un triángulo rectángulo y$c$ es su hipotenusa, entonces:

\[a^2 + b^2 = c^2 \nonumber \]

Decimos “La suma de los cuadrados de las patas de un triángulo rectángulo es igual al cuadrado de su hipotenusa”.

Buena pista: Tenga en cuenta que la hipotenusa se asienta sola en un lado de la ecuación$a^2 + b^2 = c^2$. Las piernas de la hipotenusa están del otro lado.

Pongamos a trabajar el Teorema de Pitágoras.

Ejemplo$\PageIndex{4}$

Encuentra la longitud del lado faltante del triángulo rectángulo que se muestra a continuación.

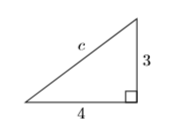
$higo 8.2.4.png$

Solución

Primero, escribir el Teorema de Pitágoras, luego sustituir los valores dados en los lugares apropiados.

\[\begin{aligned} a^{2}+b^{2}=c^{2} & \color {Red} \text { Pythagorean Theorem. } \\(4)^{2}+(3)^{2}=c^{2} & \color {Red} \text { Substitute: } 4 \text { for } a, 3 \text { for } b \\ 16+9=c^{2} & \color {Red} \text { Square: }(4)^{2}=16,(3)^{2}=9 \\ 25=c^{2} & \color {Red} \text { Add: } 16+9=25 \end{aligned} \nonumber \]

La ecuación$c^2 = 25$ tiene dos soluciones reales,$c = −5$ y$c = 5$. Sin embargo, en esta situación,$c$ representa la longitud de la hipotenusa y debe ser un número positivo. Por lo tanto:

\[c=5 \quad \color {Red} \text { Nonnegative square root. } \nonumber \]

Así, la longitud de la hipotenusa es$5$.

Ejercicio$\PageIndex{4}$

Encuentra el lado faltante del triángulo derecho que se muestra a continuación.

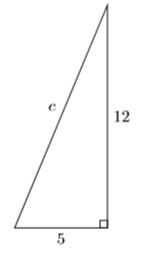
$Ex 8.2.4.png$

Contestar: $13$

Ejemplo$\PageIndex{5}$

Un triángulo rectángulo isósceles tiene una hipotenusa de longitud$8$. Encuentra los largos de las piernas.

Solución

En general, un triángulo isósceles es un triángulo con dos lados iguales. En este caso, un triángulo rectángulo isósceles tiene dos patas iguales. Vamos a dejar$x$ representar la longitud de cada pierna.

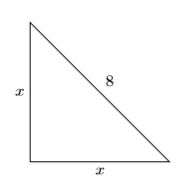
$higo 8.2.5.png$

Utilizar el Teorema de Pitágoras, sustituyendo$x$ cada pierna y$8$ por la hipotenusa.

\[\begin{array}{rlrl}{a^{2}+b^{2}} & {=c^{2}} & {} & \color {Red} {\text { Pythagorean Theorem. }} \\ {x^{2}+x^{2}} & {=8^{2}} & {} & \color {Red} {\text { Substitute: } x \text { for } a, x \text { for } b, 8 \text { for } c .} \\ {2 x^{2}} & {=64} & {} & \color {Red} {\text { Combine like terms: } x+x=2 x} \\ {x^{2}} & {=32} & {} & \color {Red} {\text { Divide both sides by } 2}\end{array} \nonumber \]

La ecuación$x^2 = 32$ tiene dos soluciones reales,$x=-\sqrt{32}$ y$x=\sqrt{32}$. No obstante, en esta situación,$x$ representa la longitud de cada tramo y debe ser un número positivo. Por lo tanto:

\[x=\sqrt{32} \quad \color {Red} \text { Nonnegative square root. } \nonumber \]

Recuerda, tu respuesta final debe ser en forma simple y radical. Debemos faccionar un cuadrado perfecto cuando sea posible.

\[\begin{array}{ll}{x=\sqrt{16} \sqrt{2}} & \color {Red} {\text { Factor out a perfect square. }} \\ {x=4 \sqrt{2}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]

Así, la longitud de cada pierna es$4\sqrt{2}$.

Ejercicio$\PageIndex{5}$

Un triángulo rectángulo isósceles tiene una hipotenusa de longitud$10$. Encuentra los largos de las piernas.

Contestar: Cada pierna tiene longitud$5\sqrt{2}$

Aplicaciones

Probemos un problema de palabras.

Ejemplo$\PageIndex{6}$

Una escalera de$20$ pies de largo se apoya contra la pared del garaje. Si la base de la escalera está a$8$ pies de la pared del garaje, ¿qué tan alto llega la escalera a la pared del garaje? Encuentra una respuesta exacta, luego usa tu calculadora para redondear tu respuesta a la décima de pie más cercana.

Solución

Como siempre, obedecemos los Requisitos para Soluciones de Problemas de Palabras.

Configurar un diccionario de variables. Crearemos un diagrama bien marcado para este propósito, dejando$h$ representar la distancia entre la base de la pared del garaje y la punta superior de la escalera.

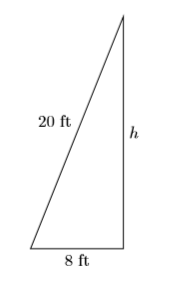
$higo 8.2.6.png$

Configure una ecuación. Usando el Teorema de Pitágoras, podemos escribir:\[\begin{array}{ll}{8^{2}+h^{2}=20^{2}} & \color {Red} {\text { Pythagorean Theorem. }} \\ {64+h^{2}=400} & \color {Red} {\text { Square: } 8^{2}=64 \text { and } 20^{2}=400}\end{array} \nonumber \]
Resuelve la ecuación. \[\begin{array}{ll}{h^{2}=336} & \color {Red} {\text { Subtract } 64 \text { from both sides. }} \\ {h=\sqrt{336}} & \color {Red} {h \text { will be the nonnegative square root. }} \\ {h=\sqrt{16} \sqrt{21}} & \color {Red} {\text { Factor out a perfect square. }} \\ {h=4 \sqrt{21}} & \color {Red} {\text { Simplify: } \sqrt{16}=4}\end{array} \nonumber \]
Contesta la pregunta. La escalera alcanza$4 \sqrt{21}$ pies arriba de la pared. Usando una calculadora, esto es aproximadamente$18.3$ pies, redondeado a la décima de pie más cercana.
Mira hacia atrás. Entiende que cuando usamos$18.3$ ft, una aproximación, nuestra solución solo verificará aproximadamente.

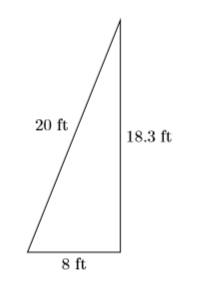
$higo 8.2.7.png$

Usando el Teorema de Pitágoras:\[\begin{array}{r}{8^{2}+18.3^{2} \stackrel{?}{=} 20^{2}} \\ {64+334.89 \stackrel{?}{=} 400} \\ {398.89 \stackrel{?}{=} 400}\end{array} \nonumber \] La aproximación no es perfecta, pero parece lo suficientemente cercana como para aceptar esta solución.

Ejercicio$\PageIndex{6}$

Una escalera de$15$ pies de largo se apoya contra una pared. Si la base de la escalera está a$6$ pies de la pared, ¿qué tan alto llega la escalera? Usa tu calculadora para redondear tu respuesta a la décima de pie más cercana.

Contestar: $13.7$pies.

Search

Text Color

Text Size

Margin Size

Font Type