Capítulo 8 Ejercicios de revisión
- Page ID
- 110303
Ejercicios de revisión de capítulos
Simplificar expresiones racionales
Determinar los valores para los cuales no está definida una expresión racional
En los siguientes ejercicios, determinar los valores para los que la expresión racional es indefinida.
\(\dfrac{2a+1}{3a−2}\)
- Responder
-
\(a \ne \dfrac{2}{3}\)
\(\dfrac{b−3}{b^2−16}\)
\(\dfrac{3xy^2}{5y}\)
- Responder
-
\(y \ne 0\)
\(\dfrac{u−3}{u^2−u−30}\)
Evaluar expresiones racionales
En los siguientes ejercicios, evaluar las expresiones racionales para los valores dados.
\(\dfrac{4p−1}{p^2+5}\)cuando\(p=−1\)
- Responder
-
\(−\dfrac{5}{6}\)
\(\dfrac{q^2−5}{q+3}\)cuando\(q=7\)
\(\dfrac{y^2−8}{y^2−y−2}\)cuando\(y=1\)
- Responder
-
\(\dfrac{7}{2}\)
\(\dfrac{z^2+2}{4z−z^2}\)cuando\(z=3\)
En los siguientes ejercicios, simplifique.
\(\dfrac{10}{24}\)
- Responder
-
\(\dfrac{5}{12}\)
\(\dfrac{8m^4}{16mn^3}\)
\(\dfrac{14a−14}{a−1}\)
- Responder
-
\(14\)
\(\dfrac{b^2+7b+12}{b^2+8b+16}\)
Simplifique las expresiones racionales con factores opuestos
En los siguientes ejercicios, simplifique.
\(\dfrac{c^2−c−2}{4−c^2}\)
- Responder
-
\(-\dfrac{c+1}{c+2}\)
\(\dfrac{d−16}{16−d}\)
\(\dfrac{7v−35}{25−v^2}\)
- Responder
-
\(−\dfrac{7}{5+v}\)
\(\dfrac{w^2−3w−28}{49−w^2}\)
Multiplicar y dividir expresiones racionales
Multiplicar expresiones racionales
En los siguientes ejercicios, multiplicar.
\(\dfrac{3}{8}·\dfrac{2}{15}\)
- Responder
-
\(\dfrac{1}{20}\)
\(\dfrac{2xy^2}{8y^3}·\dfrac{16y}{24x}\)
\(\dfrac{3a^2+21a}{a^2+6a−7}·\dfrac{a−1}{ab}\)
- Responder
-
\(\dfrac{3}{b}\)
\(\dfrac{5z^2}{5z^2+40z+35}·\dfrac{z^2−1}{3z}\)
Dividir expresiones racionales
En los siguientes ejercicios, divide.
\(\dfrac{t^2−4t-12}{t^2+8t+12}÷\dfrac{t^2−36}{6t}\)
- Responder
-
\(\dfrac{6t}{(t+6)^2}\)
\(\dfrac{r^2−16}{4}÷\dfrac{r^3−64}{2r^2−8r+32}\)
\(\dfrac{11+w}{w−9}÷\dfrac{121−w^2}{9−w}\)
- Responder
-
\(\dfrac{1}{11+w}\)
\(\dfrac{3y^2−12y−63}{4y+3}÷(6y^2−42y)\)
\(\dfrac{\dfrac{c^2−64}{3c^2+26c+16}}{\dfrac{c^2−4c−32}{15c+10}}\)
- Responder
-
\(5c+4\)
\(\dfrac{8m^2−8m}{m−4}·\dfrac{m^2+2m−24}{m^2+7m+10}÷\dfrac{2m^2−6m}{m+5}\)
Sumar y restar expresiones racionales con un denominador común
Agregar expresiones racionales con un denominador común
En los siguientes ejercicios, agregue.
\(\dfrac{3}{5}+\dfrac{2}{5}\)
- Responder
-
\(1\)
\(\dfrac{4a^2}{2a−1}−\dfrac{1}{2a−1}\)
\(\dfrac{p^2+10p}{p+5}+\dfrac{25}{p+5}\)
- Responder
-
\(p+5\)
\(\dfrac{3x}{x−1}+\dfrac{2}{x−1}\)
Restar expresiones racionales con un denominador común
En los siguientes ejercicios, restar.
\(\dfrac{d^2}{d+4}−\dfrac{3d+28}{d+4}\)
- Responder
-
\(d-7\)
\(\dfrac{z^2}{z+10}−\dfrac{100}{z+10}\)
\(\dfrac{4q^2−q+3}{q^2+6q+5}−\dfrac{3q^2+q+6}{q^2+6q+5}\)
- Responder
-
\(\dfrac{q−3}{q+5}\)
\(\dfrac{5t+4t+3}{t^2−25}−\dfrac{4t^2−8t−32}{t^2−25}\)
En los siguientes ejercicios, sumar y restar.
\(\dfrac{18w}{6w−1}+\dfrac{3w−2}{1−6w}\)
- Responder
-
\(\dfrac{15w+2}{6w−1}\)
\(\dfrac{a^2+3a}{a^2−4}−\dfrac{3a−8}{4−a^2}\)
\(\dfrac{2b^2+3b−15}{b^2−49}−\dfrac{b^2+16b−1}{49−b^2}\)
- Responder
-
\(\dfrac{3b−2}{b+7}\)
\(\dfrac{8y^2−10y+7}{2y−5}+\dfrac{2y^2+7y+2}{5−2y}\)
Sumar y restar expresiones racionales con denominadores diferentes
Encuentre el denominador menos común de las expresiones racionales
En los siguientes ejercicios, encuentra el LCD.
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\)
- Responder
-
\((m+2)(m−5)(m+4)\)
\(\dfrac{6}{n^2−4},\quad\dfrac{2n}{n^2−4n+4}\)
\(\dfrac{5}{3p^2+17p−6},\quad\dfrac{2m}{3p^2−23p−8}\)
- Responder
-
\((3p+1)(p+6)(p+8)\)
En los siguientes ejercicios, reescribe como expresiones racionales equivalentes con el denominador dado.
Reescribir como expresiones racionales equivalentes con denominador\((m+2)(m−5)(m+4)\)
\(\dfrac{4}{m^2−3m−10},\quad\dfrac{2m}{m^2−m−20}\).
Reescribir como expresiones racionales equivalentes con denominador\((n−2)(n−2)(n+2)\)
\(\dfrac{6}{n^2−4n+4},\quad\dfrac{2n}{n^2−4}\).
- Responder
-
\(\dfrac{6n+12}{(n−2)(n−2)(n+2)},\quad\dfrac{2n^2−4n}{(n−2)(n−2)(n+2)}\)
Reescribir como expresiones racionales equivalentes con denominador\((3p+1)(p+6)(p+8)\)
\(\dfrac{5}{3p^2+19p+6},\quad\dfrac{7p}{3p^2+25p+8}\)
En los siguientes ejercicios, agregue.
\(\dfrac{2}{3}+\dfrac{3}{5}\)
- Responder
-
\(\dfrac{19}{15}\)
\(\dfrac{7}{5a}+\dfrac{3}{2b}\)
\(\dfrac{2}{c−2}+\dfrac{9}{c+3}\)
- Responder
-
\(\dfrac{11c−12}{(c−2)(c+3)}\)
\(\dfrac{3d}{d^2−9}+\dfrac{5}{d^2+6d+9}\)
\(\dfrac{2x}{x^2+10x+24}+\dfrac{3x}{x^2+8x+16}\)
- Responder
-
\(\dfrac{5x^2+26x}{(x+4)(x+4)(x+6)}\)
\(\dfrac{5q}{p^{2}q−p^2}+\dfrac{4q}{q^2−1}\)
En los siguientes ejercicios, restar y sumar.
\(\dfrac{3v}{v+2}−\dfrac{v+2}{v+8}\)
- Responder
-
\(\dfrac{2(v^2+10v−2)}{(v+2)(v+8)}\)
\(\dfrac{−3w−15}{w^2+w−20}−\dfrac{w+2}{4−w}\)
\(\dfrac{7m+3}{m+2}−5\)
- Responder
-
\(\dfrac{2m−7}{m+2}\)
\(\dfrac{n}{n+3}+\dfrac{2}{n−3}−\dfrac{n−9}{n^2−9}\)
\(\dfrac{8d}{d^2−64}−\dfrac{4}{d+8}\)
- Responder
-
\(4d−8\)
\(\dfrac{5}{12x^{2}y}+\dfrac{7}{20xy^3}\)
Simplificar expresiones racionales complejas
Simplifique una expresión racional compleja escribiéndola como división
En los siguientes ejercicios, simplifique.
\(\dfrac{\dfrac{5a}{a+2}}{\dfrac{10a^2}{a^2−4}}\)
- Responder
-
\(\dfrac{a−2}{2a}\)
\(\dfrac{\dfrac{2}{5}+\dfrac{5}{6}}{\dfrac{1}{3}+\dfrac{1}{4}}\)
\(\dfrac{x−\dfrac{3x}{x+5}}{\dfrac{1}{x+5}+\dfrac{1}{x−5}}\)
- Responder
-
\(\dfrac{(x−8)(x−5)}{2}\)
\(\dfrac{\dfrac{2}{m}+\dfrac{m}{n}}{\dfrac{n}{m}−\dfrac{1}{n}}\)
En los siguientes ejercicios, simplifique.
\(\dfrac{6+\dfrac{2}{q−4}}{\dfrac{5}{q}+4}\)
- Responder
-
\(\dfrac{(q−2)(q+4)}{5(q−4)}\)
\(\dfrac{\dfrac{3}{a^2}−\dfrac{1}{b}}{\dfrac{1}{a}+\dfrac{1}{b^2}}\)
\(\dfrac{\dfrac{2}{z^2−49}+\dfrac{1}{z+7}}{\dfrac{9}{z+7}+\dfrac{12}{z−7}}\)
- Responder
-
\(\dfrac{z−5}{21z+21}\)
\(\dfrac{\dfrac{3}{y^2−4y−32}}{\dfrac{2}{y−8}+\dfrac{1}{y+4}}\)
Resolver ecuaciones racionales
Resolver ecuaciones racionales
En los siguientes ejercicios, resuelve.
\(\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{1}{x}\)
- Responder
-
\(\dfrac{6}{7}\)
\(1−\dfrac{2}{m}=\dfrac{8}{m^2}\)
\(\dfrac{1}{b−2}+\dfrac{1}{b+2}=\dfrac{3}{b^2−4}\)
- Responder
-
\(\dfrac{3}{2}\)
\(\dfrac{3}{q+8}−\dfrac{2}{q−2}=1\)
\(\dfrac{v−15}{v^2−9v+18}=\dfrac{4}{v−3}+\dfrac{2}{v−6}\)
- Responder
-
no hay solución
\(\dfrac{z}{12}+\dfrac{z+3}{3z}=\dfrac{1}{z}\)
Resolver una ecuación racional para una variable específica
En los siguientes ejercicios, resuelva para la variable indicada.
\(\dfrac{V}{l}=hw\)para\(l\)
- Responder
-
\(l=\dfrac{V}{hw}\)
\(\dfrac{1}{x}−\dfrac{2}{y}=5\)para\(y\)
\(x=\dfrac{y+5}{z−7}\)para\(z\)
- Responder
-
\(z=\dfrac{y+5+7x}{x}\)
\(P=\dfrac{k}{V}\)para\(V\)
Resolver Proporción y Similares Figuras Similares
Resolver proporciones
En los siguientes ejercicios, resuelve.
\(\dfrac{x}{4}=\dfrac{3}{5}\)
- Responder
-
\(\dfrac{12}{5}\)
\(\dfrac{3}{y}=\dfrac{9}{5}\)
\(\dfrac{s}{s+20}=\dfrac{3}{7}\)
- Responder
-
\(15\)
\(\dfrac{t−3}{5}=\dfrac{t+2}{9}\)
En los siguientes ejercicios, resuelve usando proporciones.
Rachael tenía un batido de fresa de\(21\) onza que tiene\(739\) calorías. ¿Cuántas calorías hay en un batido de\(32\) onza?
- Responder
-
\(1161\)calorías
Leo fue a México durante las vacaciones navideñas y cambió\($525\) dólares a pesos mexicanos. En ese momento, el tipo de cambio que tenía\($1\) EU es igual a pesos\(16.25\) mexicanos. ¿Cuántos pesos mexicanos obtuvo para su viaje?
En los siguientes ejercicios, resuelve.
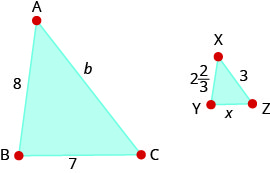
\(∆ABC\)es similar a\(∆XYZ\). Las longitudes de dos lados de cada triángulo se dan en la figura. Encuentra las longitudes de los terceros lados.
- Responder
-
\(b=9\);\(x=2\dfrac{1}{3}\)
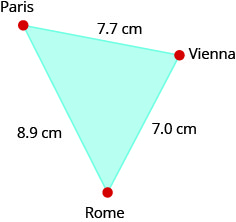
En un mapa de Europa, París, Roma y Viena forman un triángulo cuyos lados se muestran en la siguiente figura. Si la distancia real de Roma a Viena es\(700\) millas, encuentre la distancia de
- a. París a Roma
- b. de París a Viena
Tony mide\(5.75\) pies de altura. Una tarde, su sombra tenía\(8\) pies de largo. Al mismo tiempo, la sombra de un árbol cercano tenía\(32\) pies de largo. Encuentra la altura del árbol.
- Responder
-
\(23\)pies
La altura de un faro en Pensacola, Florida es de\(150\) pies. De pie junto a la estatua, un\(5.5\) pie de altura Natalie proyectó una sombra de\(1.1\) pie ¿Cuánto tiempo sería la sombra del faro?
Resolver problemas de movimiento uniforme y aplicaciones de trabajo
Resolver aplicaciones de movimiento uniforme
En los siguientes ejercicios, resuelve.
Al hacer el viaje de 5 horas a casa después de visitar a sus padres, Lisa se topó con el mal tiempo. Ella pudo conducir\(176\) millas mientras hacía buen tiempo, pero luego manejando\(10\) mph más lento, se fue\(81\) millas con el mal tiempo. ¿Qué tan rápido manejaba cuando hacía mal tiempo?
- Contestar
-
45 mph
Mark está montando en un avión que puede volar\(490\) millas con un viento de cola de\(20\) mph al mismo tiempo que puede volar\(350\) millas contra un viento de cola de\(20\) mph. ¿Cuál es la velocidad del avión?
John puede andar en bicicleta\(8\) mph más rápido que Luke puede andar en su bicicleta. A Luke le toma\(3\) horas más que a John recorrer\(48\) millas. ¿Qué tan rápido puede John andar en bicicleta?
- Contestar
-
\(16\)mph
Mark estaba entrenando para un triatlón. Corrió\(8\) kilómetros y recorrió\(32\) kilómetros en bicicleta en un total de\(3\) horas. Su velocidad de carrera era\(8\) kilómetros por hora menos que su velocidad de ciclismo. ¿Cuál era su velocidad de carrera?
En los siguientes ejercicios, resuelve.
Jerry puede enmarcar una habitación en una\(1\) hora, mientras que Jake toma\(4\) horas. ¿Cuánto tiempo podrían enmarcar una habitación trabajando juntos?
- Contestar
-
\(\dfrac{4}{5}\)hora
Lisa tarda\(3\) horas en cortar el césped mientras que su prima, Barb, toma\(2\) horas. ¿Cuánto tiempo les llevará trabajar juntos?
Jeffrey puede pintar una casa en\(6\) días, pero si consigue un ayudante puede hacerlo en\(4\) días. ¿Cuánto tiempo tardaría el ayudante en pintar la casa sola?
- Contestar
-
\(12\)días
Sue y Deb trabajan juntos escribiendo un libro que les lleva\(90\) días. Si Sue trabajara sola le llevaría\(120\) días. ¿Cuánto tardaría Deb en escribir el libro sola?
Usar variación directa e inversa
Resolver problemas de variación directa
En los siguientes ejercicios, resuelve.
Si\(y\) varía directamente como\(x\), cuándo\(y=9\) y\(x=3\), encontrar\(x\) cuándo\(y=21\).
- Contestar
-
\(7\)
Si\(y\) varía directamente como\(x\), cuándo\(y=20\) y\(x=2\), encontrar\(y\) cuándo\(x=4\).
Si\(m\) varía inversamente con el cuadrado de\(n\), cuándo\(m=4\) y\(n=6\), encontrar\(m\) cuándo\(n=2\).
- Contestar
-
\(36\)
Vanessa viaja para ver a su prometido. La distancia,\(d\), varía directamente con la velocidad,\(v\), ella conduce. Si viaja\(258\) millas conduciendo\(60\) mph, ¿qué tan lejos viajaría yendo\(70\) mph?
Si el costo de una pizza varía directamente con su diámetro, y si cuesta una pizza de\(8\)” diámetro\($12\), ¿cuánto costaría una pizza de\(6\)” diámetro?
- Contestar
-
\($9\)
La distancia para detener un automóvil varía directamente con el cuadrado de su velocidad. Se necesitan\(200\) pies para detener un auto que va\(50\) mph. ¿Cuántos pies se necesitarían para detener un auto yendo\(60\) mph?
En los siguientes ejercicios, resuelve.
El número de boletos para una recaudación de fondos de música varía inversamente con el precio de los boletos. Si Madelyn tiene el dinero suficiente para comprar\(12\) boletos\($6\), ¿cuántos boletos puede permitirse Madelyn comprar si el precio aumentaba a\($8\)?
- Contestar
-
\(97\)boletos
En un instrumento de cuerda, la longitud de una cuerda varía inversamente con la frecuencia de sus vibraciones. Si una cuerda de\(11\) -pulgada en un violín tiene una frecuencia de\(360\) ciclos por segundo, ¿qué frecuencia tiene una cuerda de\(12\) -pulgada?
Prueba de práctica
En los siguientes ejercicios, simplifique.
\(\dfrac{3a^{2}b}{6ab^2}\)
- Contestar
-
\(\dfrac{a}{2b}\)
\(\dfrac{5b−25}{b^2−25}\)
En los siguientes ejercicios, realice la operación indicada y simplifique.
\(\dfrac{4x}{x+2}·\dfrac{x^2+5x+6}{12x^2}\)
- Contestar
-
\(\dfrac{x+3}{3x}\)
\(\dfrac{5y}{4y−8}·\dfrac{y^2−4}{10}\)
\(\dfrac{4p}{q}+\dfrac{5}{p}\)
- Contestar
-
\(\dfrac{4+5q}{pq}\)
\(\dfrac{1}{z−9}−\dfrac{3}{z+9}\)
\(\dfrac{\dfrac{2}{3}+\dfrac{3}{5}}{\dfrac{2}{5}}\)
- Contestar
-
\(\dfrac{19}{16}\)
\(\dfrac{\dfrac{1}{m}−\dfrac{1}{n}}{\dfrac{1}{n}+\dfrac{1}{m}}\)
En los siguientes ejercicios, resuelve cada ecuación.
\(\dfrac{1}{2}+\dfrac{2}{7}=\dfrac{1}{x}\)
- Contestar
-
\(x = \dfrac{14}{11}\)
\(\dfrac{5}{y−6}=\dfrac{3}{y+6}\)
\(\dfrac{1}{z−5}+\dfrac{1}{z+5}=\dfrac{1}{z^2−25}\)
- Contestar
-
\(z = \dfrac{1}{2}\)
\(\dfrac{t}{4}=\dfrac{3}{5}\)
\(\dfrac{2}{r−2}=\dfrac{3}{r−1}\)
- Contestar
-
\(r = 4\)
En los siguientes ejercicios, resuelve.
Si\(y\) varía directamente con\(x\), y\(x=5\) cuándo\(y=30\), encontrar\(x\) cuándo\(y=42\).
Si\(y\) varía inversamente con\(x\) y\(x=6\) cuándo\(y=20\), encuentra\(y\) cuándo\(x=2\).
- Contestar
-
\(y=60\)
Si\(y\) varía inversamente con el cuadrado de\(x\) y\(x=3\) cuándo\(y=9\), encuentra\(y\) cuándo\(x=4\).
La dosis recomendada de eritromicina para perros, es de\(5\) mg por cada libra que pesa el perro. Si Daisy pesa\(25\) libras, ¿cuántos miligramos de eritromicina debe recetar su veterinario?
- Contestar
-
\(125\)mg
Julia pasó\(4\) horas el domingo por la tarde haciendo ejercicio en el gimnasio. Corrió en la cinta de correr por\(10\) millas y luego andar en bicicleta por\(20\) millas. Su velocidad de ciclismo era\(5\) mph más rápida que su velocidad de carrera en la cinta de correr. ¿Cuál era su velocidad de carrera?
Kurt puede andar en bicicleta por\(30\) kilómetros con el viento en la misma cantidad de tiempo que puede recorrer\(21\) millas contra el viento. Si la velocidad del viento es\(6\) mph, ¿cuál es la velocidad de Kurt en su bicicleta?
- Contestar
-
\(14\)mph
Amanda corre a las\(8\) millas del parque usando una ruta y luego regresa por una ruta\(14\) de millas. El viaje de regreso le lleva\(1\) una hora más que su trote al parque. Encuentra su tasa de jogging.
Un experimentado lavacristales puede lavar todas las ventanas de la casa de Mike en\(2\) horas, mientras que un nuevo aprendiz puede lavar todas las ventanas en\(7\) horas. ¿Cuánto tiempo les llevaría trabajar juntos?
- Contestar
-
\(1\frac{5}{9}\)hora
Josh puede dividir un camión lleno de troncos en\(8\) horas, pero trabajando con su papá pueden hacerlo en\(3\) horas. ¿Cuánto tardaría el padre de Josh trabajando solo en dividir los troncos?
El precio que Tyler paga por la gasolina varía directamente con la cantidad de galones que compra. Si\(24\) los galones le cuestan\($59.76\), ¿cuánto costarían\(30\) los galones?
- Contestar
-
\($74.70\)
El volumen de un gas en un contenedor varía inversamente con la presión sobre el gas. Si un recipiente de nitrógeno tiene un volumen de\(29.5\) litros con\(2000\) psi, ¿cuál es el volumen si el tanque tiene una clasificación de\(14.7\) psi? Redondear al número entero más cercano.
Las ciudades de Dayton, Columbus y Cincinnati forman un triángulo en el sur de Ohio, como se muestra en la siguiente figura, que da las distancias del mapa entre estas ciudades en pulgadas.
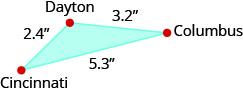
La distancia real de Dayton a Cincinnati es de\(48\) millas. ¿Cuál es la distancia real entre Dayton y Columbus?
- Contestar
-
\(64\)millas