Capítulo 9 Ejercicios de revisión
- Page ID
- 110158
Capítulo 9 Ejercicios de revisión
Simplificar y usar raíces cuadradas
Simplifique las expresiones con raíces cuadradas
En los siguientes ejercicios, simplifique.
\(\sqrt{64}\)
\(\sqrt{144}\)
- Contestar
-
12
\(−\sqrt{25}\)
\(−\sqrt{81}\)
- Contestar
-
−9
\(\sqrt{−9}\)
\(\sqrt{−36}\)
- Contestar
-
no es un número real
\(\sqrt{64}+\sqrt{225}\)
\(\sqrt{64+225}\)
- Contestar
-
17
En los siguientes ejercicios, estime cada raíz cuadrada entre dos números enteros consecutivos.
\(\sqrt{28}\)
\(\sqrt{155}\)
- Contestar
-
\(12<\sqrt{155}<13\)
Raíces Cuadradas Aproximadas
En los siguientes ejercicios, aproximar cada raíz cuadrada y redondear a dos decimales.
\(\sqrt{15}\)
\(\sqrt{57}\)
- Contestar
-
7.55
Simplifique las expresiones variables con raíces cuadradas
En los siguientes ejercicios, simplifique.
\(\sqrt{q^2}\)
\(\sqrt{64b^2}\)
- Contestar
-
8b
\(−\sqrt{121a^2}\)
\(\sqrt{225m^{2}n^{2}}\)
- Contestar
-
15mn
\(−\sqrt{100q^2}\)
\(\sqrt{49y^2}\)
- Contestar
-
7y
\(\sqrt{4a^{2}b^{2}}\)
\(\sqrt{121c^{2}d^{2}}\)
- Contestar
-
11cd
Simplifique las raíces cuadradas
Utilice la propiedad del producto para simplificar las raíces cuadradas
En los siguientes ejercicios, simplifique.
\(\sqrt{300}\)
\(\sqrt{98}\)
- Contestar
-
\(7\sqrt{2}\)
\(\sqrt{x^{13}}\)
\(\sqrt{y^{19}}\)
- Contestar
-
\(y^{9}\sqrt{y}\)
\(\sqrt{16m^4}\)
\(\sqrt{36n^{13}}\)
- Contestar
-
\(6n^{6}\sqrt{n}\)
\(\sqrt{288m^{21}}\)
\(\sqrt{150n^7}\)
- Contestar
-
\(5n^3\sqrt{6n}\)
\(\sqrt{48r^{5}s^{4}}\)
\(\sqrt{108r^{5}s^{3}}\)
- Contestar
-
\(6r^{2}s\sqrt{3rs}\)
\(\frac{10−\sqrt{50}}{5}\)
\(\frac{6+\sqrt{72}}{6}\)
- Contestar
-
\(1+\sqrt{2}\)
En los siguientes ejercicios, simplifique.
\(\sqrt{\frac{16}{25}}\)
\(\sqrt{\frac{81}{36}}\)
- Contestar
-
\(\frac{3}{2}\)
\(\sqrt{\frac{x^8}{x^4}}\)
\(\sqrt{\frac{y^6}{y^2}}\)
- Contestar
-
\(y^2\)
\(\sqrt{\frac{98p^6}{2p^2}}\)
\(\sqrt{\frac{72q^8}{2q^4}}\)
- Contestar
-
\(6q^2\)
\(\sqrt{\frac{65}{121}}\)
\(\sqrt{\frac{26}{169}}\)
- Contestar
-
\(\frac{\sqrt{26}}{13}\)
\(\sqrt{\frac{64x^4}{25x^2}}\)
\(\sqrt{\frac{36r^{10}}{16r^5}}\)
- Contestar
-
\(\frac{3r^2\sqrt{r}}{2}\)
\(\sqrt{\frac{48p^{3}q^{5}}{27pq}}\)
\(\sqrt{\frac{12r^{5}s^{7}}{75r^{2}s}}\)
- Contestar
-
\(\frac{2rs^3\sqrt{r}}{5}\)
Suma y resta raíces cuadradas
Sumar y restar como raíces cuadradas
En los siguientes ejercicios, simplifique.
\(3\sqrt{2}+\sqrt{2}\)
\(5\sqrt{5}+7\sqrt{5}\)
- Contestar
-
\(12\sqrt{5}\)
\(4\sqrt{y}+4\sqrt{y}\)
\(6\sqrt{m}−2\sqrt{m}\)
- Contestar
-
\(4\sqrt{m}\)
\(−3\sqrt{7}+2\sqrt{7}−\sqrt{7}\)
\(8\sqrt{13}+2\sqrt{3}+3\sqrt{13}\)
- Contestar
-
\(11\sqrt{13}+2\sqrt{3}\)
\(3\sqrt{5xy}−\sqrt{5xy}+3\sqrt{5xy}\)
\(2\sqrt{3rs}+\sqrt{3rs}−5\sqrt{rs}\)
- Contestar
-
\(3\sqrt{3rs}−5\sqrt{rs}\)
Sumar y restar raíces cuadradas que necesitan simplificación
En los siguientes ejercicios, simplifique.
\(\sqrt{32}+3\sqrt{2}\)
\(\sqrt{8}+\sqrt{32}\)
- Contestar
-
\(5\sqrt{2}\)
\(\sqrt{72}+\sqrt{50}\)
\(\sqrt{48}+\sqrt{75}\)
- Contestar
-
\(9\sqrt{3}\)
\(3\sqrt{32}+\sqrt{98}\)
\(\frac{1}{3}\sqrt{27}−\frac{1}{8}\sqrt{192}\)
- Contestar
-
0
\(\sqrt{50y^5}−\sqrt{72y^5}\)
Agrega texto de ejercicios aquí.
- Contestar
-
\(17n^2\sqrt{2}\)
Multiplicar raíces cuadradas
En los siguientes ejercicios, simplifique.
\(\sqrt{2}·\sqrt{20}\)
\(2\sqrt{2}·6\sqrt{14}\)
- Contestar
-
\(24\sqrt{7}\)
\(\sqrt{2m^2}·\sqrt{20m^4}\)
\((\sqrt{62y})(\sqrt{350y^3})\)
- Contestar
-
\(180y^2\)
\((6\sqrt{3v^4})(5\sqrt{30v})\)
\((\sqrt{8})^2\)
- Contestar
-
8
\((−\sqrt{10})^2\)
\((2\sqrt{5})(5\sqrt{5})\)
- Contestar
-
50
\((−3\sqrt{3})(5\sqrt{18})\)
En los siguientes ejercicios, simplifique.
\(10(2−\sqrt{7})\)
- Contestar
-
\(20−10\sqrt{7}\)
\(\sqrt{3}(4+\sqrt{12})\)
\((5+\sqrt{2})(3−\sqrt{2})\)
- Contestar
-
\(13−2\sqrt{2}\)
\((5−3\sqrt{7})(1−2\sqrt{7})\)
\((1−3\sqrt{x})(5+2\sqrt{x})\)
- Contestar
-
\(5−13\sqrt{x}−6x\)
\((3+4\sqrt{y})(10−\sqrt{y})\)
\((1+6\sqrt{p})^2\)
- Contestar
-
\(1+12\sqrt{p}+36p\)
\((2−6\sqrt{5})^2\)
\((3+2\sqrt{7})(3−2\sqrt{7})\)
- Contestar
-
−19
\((6−\sqrt{11})(6+\sqrt{11})\)
Dividir raíces cuadradas
Dividir raíces cuadradas
En los siguientes ejercicios, simplifique.
\(\frac{\sqrt{75}}{10}\)
- Contestar
-
\(\frac{\sqrt{3}}{2}\)
\(\frac{2−\sqrt{12}}{6}\)
\(\frac{\sqrt{48}}{\sqrt{27}}\)
- Contestar
-
\(\frac{4}{3}\)
\(\frac{\sqrt{75x^7}}{\sqrt{3x^3}}\)
\(\frac{\sqrt{20y^5}}{\sqrt{2y}}\)
- Contestar
-
\(y^2\sqrt{10}\)
\(\frac{\sqrt{98p^{6}q^{4}}}{\sqrt{2p^{4}q^{8}}}\)
En los siguientes ejercicios, racionalizar el denominador.
\(\frac{10}{\sqrt{15}}\)
- Contestar
-
\(\frac{2\sqrt{15}}{3}\)
\(\frac{6}{\sqrt{6}}\)
\(\frac{5}{3\sqrt{5}}\)
- Contestar
-
\(\frac{\sqrt{5}}{3}\)
\(\frac{10}{2\sqrt{6}}\)
\(\sqrt{\frac{3}{28}}\)
- Contestar
-
\(\frac{\sqrt{21}}{14}\)
\(\sqrt{\frac{9}{75}}\)
En los siguientes ejercicios, racionalizar el denominador.
\(\frac{4}{4+\sqrt{27}}\)
- Contestar
-
\(\frac{16−12\sqrt{3}}{−11}\)
\(\frac{5}{2−\sqrt{10}}\)
\(\frac{4}{2−\sqrt{5}}\)
- Contestar
-
\(−8−4\sqrt{5}\)
\(\frac{5}{4−\sqrt{8}}\)
\(\frac{\sqrt{2}}{\sqrt{p}+\sqrt{3}}\)
- Contestar
-
\(\frac{\sqrt{2p}−\sqrt{6}}{p−3}\)
\(\frac{\sqrt{x}−\sqrt{2}}{\sqrt{x}+\sqrt{2}}\)
Resolver ecuaciones con raíces cuadradas
Resolver ecuaciones radicales
En los siguientes ejercicios, resuelve la ecuación.
\(\sqrt{7z+1}=6\)
- Contestar
-
5
\(\sqrt{4u−2}−4=0\)
\(\sqrt{6m+4}−5=0\)
- Contestar
-
\(\frac{7}{2}\)
\(\sqrt{2u−3}+2=0\)
\(\sqrt{u−4}+4=u\)
- Contestar
-
no hay solución
\(\sqrt{v−9}+9=0\)
\(\sqrt{r−4}−r=−10\)
- Contestar
-
13
\(\sqrt{s−9}−s=−9\)
\(2\sqrt{2x−7}−4=8\)
- Contestar
-
\(\frac{43}{2}\)
\(\sqrt{2−x}=\sqrt{2x−7}\)
\(\sqrt{a}+3=\sqrt{a+9}\)
- Contestar
-
0
\(\sqrt{r}+3=\sqrt{r+4}\)
\(\sqrt{u}+2=\sqrt{u+5}\)
- Contestar
-
\(\frac{11}{6}\)
\(\sqrt{n+11}−1=\sqrt{n+4}\)
\(\sqrt{y+5}+1=\sqrt{2y+3}\)
- Contestar
-
11
En los siguientes ejercicios, resuelve. Redondear aproximaciones a un decimal.
Un palé de césped cubrirá un área de aproximadamente 600 pies cuadrados. Trinh quiere pedir una paleta de césped para hacer un césped cuadrado en su patio trasero. Usa la fórmula\(s=\sqrt{A}\) para encontrar la longitud de cada lado de su césped.
Un helicóptero arrojó un paquete desde una altura de 900 pies sobre un excursionista varado. Usa la fórmula\(t=\frac{\sqrt{h}}{4}\) para encontrar cuántos segundos tardó el paquete en llegar al excursionista.
- Contestar
-
7.5 segundos
El oficial Morales midió las marcas de derrape de uno de los autos involucrados en un accidente. La longitud de las marcas de derrape era de 245 pies. Usa la fórmula\(s=\sqrt{24d}\) para encontrar la velocidad del auto antes de que se aplicaran los frenos.
Raíces Superiores
Simplifique las expresiones con raíces superiores
En los siguientes ejercicios, simplifique.
- \(\sqrt[6]{64}\)
- \(\sqrt[3]{64}\)
- Contestar
-
- 2
- 4
- \(\sqrt[3]{−27}\)
- \(\sqrt[4]{−64}\)
- \(\sqrt[9]{d^9}\)
- \(\sqrt[8]{v^8}\)
- Contestar
-
- d
- |v|
- \(\sqrt[5]{a^{10}}\)
- \(\sqrt[3]{b^{27}}\)
- \(\sqrt[4]{16x^8}\)
- \(\sqrt[6]{64y^{12}}\)
- Contestar
-
- \(2x^2\)
- \(2y^2\)
- \(\sqrt[7]{128r^{14}}\)
- \(\sqrt[4]{81s^{24}}\)
Utilice la propiedad Product para simplificar expresiones con raíces más altas
En los siguientes ejercicios, simplifique.
- \(\sqrt[9]{d^9}\)
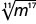
- Contestar
-
- d
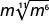
- \(\sqrt[3]{54}\)
- \(\sqrt[4]{128}\)
- \(\sqrt[5]{64c^8}\)
- \(\sqrt[4]{48d^7}\)
- Contestar
-
- \(2c\sqrt[5]{2c^3}\)
- \(2d\sqrt[4]{3d^3}\)
- \(\sqrt[3]{343q^7}\)
- \(\sqrt[6]{192r^9}\)
- \(\sqrt[3]{−500}\)
- \(\sqrt[4]{−16}\)
- Contestar
-
- \(−5\sqrt[3]{4}\)
- no es un número real
En los siguientes ejercicios, simplifique.
\(\sqrt[5]{\frac{r^{10}}{r^5}}\)
\(\sqrt[3]{\frac{w^{12}}{w^2}}\)
- Contestar
-
\(w^3\sqrt[3]{w}\)
\(\sqrt[4]{\frac{64y^8}{4y^5}}\)
\(\sqrt[3]{\frac{54z^9}{2z^3}}\)
- Contestar
-
\(3z^2\)
\(\sqrt[6]{\frac{64a^7}{b^2}}\)
En los siguientes ejercicios, simplifique.
\(4\sqrt[5]{20}−2\sqrt[5]{20}\)
- Contestar
-
\(2\sqrt[5]{20}\)
\(4\sqrt[3]{18}+3\sqrt[3]{18}\)
\(\sqrt[4]{1250}−\sqrt[4]{162}\)
- Contestar
-
\(2\sqrt[4]{2}\)
\(\sqrt[3]{640c^5}−\sqrt[3]{−80c^3}\)
\(\sqrt[5]{96t^8}+\sqrt[5]{486t^4}\)
- Contestar
-
\(2t^\sqrt[5]{3t^3}+3\sqrt[5]{2t^4}\)
Exponentes racionales
Simplifique las expresiones con\(a^{\frac{1}{n}}\)
En los siguientes ejercicios, escribe como expresión radical.
\(r^{\frac{1}{8}}\)
\(s^{\frac{1}{10}}\)
- Contestar
-
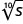
En los siguientes ejercicios, escribe con un exponente racional.
\(\sqrt[5]{u}\)
\(\sqrt[6]{v}\)
- Contestar
-
\(v^{\frac{1}{6}}\)
\(\sqrt[3]{9m}\)
\(\sqrt[6]{10z}\)
- Contestar
-
\((10z)^{\frac{1}{6}}\)
En los siguientes ejercicios, simplifique.
\(16^{\frac{1}{4}}\)
\(32^{\frac{1}{5}}\)
- Contestar
-
2
\((−125)^{\frac{1}{3}}\)
\((125)^{−\frac{1}{3}}\)
- Contestar
-
\(\frac{1}{5}\)
\((−9)^{\frac{1}{2}}\)
\((36)^{−\frac{1}{2}}\)
- Contestar
-
\(\frac{1}{6}\)
En los siguientes ejercicios, escribe con un exponente racional.
\(\sqrt[3]{q^5}\)
\(\sqrt[5]{n^8}\)
- Contestar
-
\(n^{\frac{8}{5}}\)
En los siguientes ejercicios, simplifique.
\(27^{−\frac{2}{3}}\)
\(64^{\frac{5}{2}}\)
- Contestar
-
32,768
\(36^{\frac{3}{2}}\)
\(81^{−\frac{5}{2}}\)
- Contestar
-
\(\frac{1}{59,049}\)
Utilice las leyes de los exponentes para simplificar expresiones con exponentes racionales
En los siguientes ejercicios, simplifique.
\(3^{\frac{4}{5}}·3^{\frac{6}{5}}\)
\((x^6)^{\frac{4}{3}}\)
- Contestar
-
\(x^8\)
\(\frac{z^{\frac{5}{2}}}{z^{\frac{7}{5}}}\)
\((16s^{\frac{9}{4}})^{\frac{1}{4}}\)
- Contestar
-
\(2s^{\frac{9}{16}}\)
\((m^{8}n^{12})^{\frac{1}{4}}\)
\(\frac{z^{\frac{2}{3}}·z^{−\frac{1}{3}}}{z^{−\frac{5}{3}}}\)
- Contestar
-
\(z^2\)
Prueba de práctica
En los siguientes ejercicios, simplifique.
\(\sqrt{81+144}\)
\(\sqrt{169m^{4}n^{2}}\)
- Contestar
-
\(13m^{2}|n|\)
\(\sqrt{36n^{13}}\)
\(3\sqrt{13}+5\sqrt{2}+\sqrt{13}\)
- Contestar
-
\(4\sqrt{13}+5\sqrt{2}\)
\(5\sqrt{20}+2\sqrt{125}\)
\((3\sqrt{6y})(\sqrt{250y^3})\)
- Contestar
-
\(180y^2\sqrt{3}\)
\((2−5\sqrt{x})(3+\sqrt{x})\)
\((1−2\sqrt{q})^2\)
- Contestar
-
\(1−4\sqrt{q}+4q\)
- \(\sqrt{a^{12}}\)
- \(\sqrt[3]{b^{21}}\)
- \(\sqrt[4]{81x^{12}}\)
- \(\sqrt[6]{64y^{18}}\)
- Contestar
-
- \(3x^3\)
- \(2y^3\)
\(\sqrt[6]{\frac{64r^{12}}{25r^6}}\)
\(\sqrt{\frac{14y^3}{7y}}\)
- Contestar
-
\(y\sqrt{2}\)
\(\frac{\sqrt{256x^7}}{\sqrt{54x^2}}\)
\(\sqrt[4]{512}−2\sqrt[4]{32}\)
- Contestar
-
0
- \(256^{\frac{1}{4}}\)
- \(243^{\frac{1}{5}}\)
\(49^{\frac{3}{2}}\)
- Contestar
-
343
\(25^{−\frac{5}{2}}\)
\(\frac{w^{\frac{3}{4}}}{w^{\frac{7}{4}}}\)
- Responder
-
\(\frac{1}{w}\)
\((27s^{\frac{3}{5}})^{\frac{1}{3}}\)
En los siguientes ejercicios, racionalizar el denominador.
\(\frac{3}{2\sqrt{6}}\)
- Responder
-
\(\frac{\sqrt{6}}{4}\)
\(\frac{\sqrt{3}}{\sqrt{x}+\sqrt{5}}\)
En los siguientes ejercicios, resuelve.
\(3\sqrt{2x−3}−20=7\)
- Responder
-
42
\(\sqrt{3u−2}=\sqrt{5u+1}\)
En el siguiente ejercicio, resolver.
Un helicóptero que volaba a una altitud de 600 pies arrojó un paquete a un bote salvavidas. Usa la fórmula\(t=\frac{\sqrt{h}}{4}\) para encontrar cuántos segundos tardó el paquete en llegar al excursionista. Redondea tu respuesta a la décima de segundo más cercana.
- Responder
-
6.1 segundos


