9.8E: Ejercicios

La práctica hace la perfección

Simplifique las expresiones con$a^{\frac{1}{n}}$

En los siguientes ejercicios, escribe como expresión radical.

Ejemplo$\PageIndex{47}$

1. $x^{\frac{1}{2}}$
2. $y^{\frac{1}{3}}$
3. $z^{\frac{1}{4}}$

Ejemplo$\PageIndex{48}$

1. $r^{\frac{1}{2}}$
2. $s^{\frac{1}{3}}$
3. $t^{\frac{1}{4}}$

Contestar

1. $\sqrt{r}$
2. $\sqrt[3]{s}$
3. $\sqrt[4]{t}$

Ejemplo$\PageIndex{49}$

1. $u^{\frac{1}{5}}$
2. $v^{\frac{1}{9}}$
3. $w^{\frac{1}{20}}$

Ejemplo$\PageIndex{50}$

1. $g^{\frac{1}{7}}$
2. $h^{\frac{1}{5}}$
3. $j^{\frac{1}{25}}$

Contestar

1. $\sqrt[7]{g}$
2. $\sqrt[5]{h}$
3. $\sqrt[25]{j}$

En los siguientes ejercicios, escribe con un exponente racional.

Ejemplo$\PageIndex{51}$

1. $−\sqrt[7]{x}$
2. $\sqrt[9]{y}$
3. $\sqrt[5]{f}$

Ejemplo$\PageIndex{52}$

1. $\sqrt[8]{r}$
2. $\sqrt[10]{s}$
3. \(\sqrt[4]{t}\)

Contestar

1. $r^{\frac{1}{8}}$
2. $s^{\frac{1}{10}}$
3. $t^{\frac{1}{4}}$

Ejemplo$\PageIndex{53}$

1. \ (\ sqrt [3] {a}\
2. $\sqrt[12]{b}$
3. $\sqrt{c}$

Ejemplo$\PageIndex{54}$

1. $\sqrt[5]{u}$
2. $\sqrt{v}$

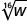
Contestar

1. $u^{\frac{1}{5}}$
2. $v^{\frac{1}{2}}$
3. $w^{\frac{1}{16}}$

Ejemplo$\PageIndex{55}$

1. $\sqrt[3]{7c}$
2. $\sqrt[7]{12d}$
3. $3\sqrt[4]{5f}$

Ejemplo$\PageIndex{56}$

1. $\sqrt[4]{5x}$
2. $\sqrt[8]{9y}$
3. $7\sqrt[5]{3z}$

Contestar

1. $(5x)^{\frac{1}{4}}$
2. $(9y)^{\frac{1}{8}}$
3. $7(3z)^{\frac{1}{5}}$

Ejemplo$\PageIndex{57}$

1. $\sqrt{21p}$
2. $\sqrt[4]{8q}$
3. $\sqrt[6]{436r}$

Ejemplo$\PageIndex{58}$

1. $\sqrt[3]{25a}$
2. $\sqrt{3b}$

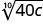
Contestar

1. $(25a)^{\frac{1}{3}}$
2. $(3b)^{\frac{1}{2}}$
3. $(40c)^{\frac{1}{10}}$

En los siguientes ejercicios, simplifique.

Ejemplo$\PageIndex{59}$

1. $81^{\frac{1}{2}}$
2. $125^{\frac{1}{3}}$
3. $64^{\frac{1}{2}}$

Ejemplo$\PageIndex{60}$

1. $625^{\frac{1}{4}}$
2. $243^{\frac{1}{5}}$
3. $32^{\frac{1}{5}}$

Contestar

1. 5
2. 3
3. 2

Ejemplo$\PageIndex{61}$

1. $16^{\frac{1}{4}}$
2. $16^{\frac{1}{2}}$
3. $3125^{\frac{1}{5}}$

Ejemplo$\PageIndex{62}$

1. $216^{\frac{1}{3}}$
2. $32^{\frac{1}{5}}$
3. $81^{\frac{1}{4}}$

Contestar

1. 6
2. 2
3. 3

Ejemplo$\PageIndex{63}$

1. $(−216)^{\frac{1}{3}}$
2. $−216^{\frac{1}{3}}$
3. $(216)^{−\frac{1}{3}}$

Ejemplo$\PageIndex{64}$

1. $(−243)^{\frac{1}{5}}$
2. $−243^{\frac{1}{5}}$
3. $(243)^{−\frac{1}{5}}$

Contestar

1. −3
2. −3
3. $\frac{1}{3}$

Ejemplo$\PageIndex{65}$

1. $(−1)^{\frac{1}{3}}$
2. $−1^{\frac{1}{3}}$
3. $(1)^{−\frac{1}{3}}$

Ejemplo$\PageIndex{66}$

1. $(−1000)^{\frac{1}{3}}$
2. $−1000^{\frac{1}{3}}$
3. $(1000)^{−\frac{1}{3}}$

Contestar

1. −10
2. −10
3. \ (\ frac {1} {10}

Ejemplo$\PageIndex{67}$

1. $(−81)^{\frac{1}{4}}$
2. $−81^{\frac{1}{4}}$
3. $(81)^{−\frac{1}{4}}$

Ejemplo$\PageIndex{68}$

1. $(−49)^{\frac{1}{2}}$
2. $−49^{\frac{1}{2}}$
3. $(49)^{−\frac{1}{2}}$

Contestar

1. no es un número real
2. −7
3. $\frac{1}{7}$

Ejemplo$\PageIndex{69}$

1. $(−36)^{\frac{1}{2}}$
2. $−36^{\frac{1}{2}}$
3. $(36)^{−\frac{1}{2}}$

Ejemplo$\PageIndex{70}$

1. $(−1)^{\frac{1}{4}}$
2. $(1)^{−\frac{1}{4}}$
3. $−1^{\frac{1}{4}}$

Contestar

1. no es un número real
2. 1
3. −1

Ejemplo$\PageIndex{71}$

1. $(−100)^{\frac{1}{2}}$
2. $−100^{\frac{1}{2}}$
3. $(100)^{−\frac{1}{2}}$

Ejemplo$\PageIndex{72}$

1. $(−32)^{\frac{1}{5}}$
2. $(243)^{−\frac{1}{5}}$
3. $−125^{\frac{1}{3}}$

Contestar

1. −2
2. $\frac{1}{3}$
3. −5

Simplifique las expresiones con$a^{\frac{m}{n}}$

En los siguientes ejercicios, escribe con un exponente racional.

Ejemplo$\PageIndex{73}$

1. $\sqrt{m^5}$
2. $\sqrt[3]{n^2}$
3. $\sqrt[4]{p^3}$

Ejemplo$\PageIndex{74}$

1. $\sqrt[4]{r^7}$
2. $\sqrt[5]{s^3}$
3. $\sqrt[3]{t^7}$

Contestar

1. $r^{\frac{7}{4}}$
2. $s^{\frac{3}{5}}$
3. $t^{\frac{7}{3}}$

Ejercicio$\PageIndex{75}$

1. $\sqrt[5]{u^2}$
2. $\sqrt[5]{v^8}$
3. $\sqrt[9]{w^4}$

Ejemplo$\PageIndex{76}$

1. $\sqrt[3]{a}$
2. $\sqrt[5]{b}$
3. $\sqrt[3]{c^5}$

Contestar

1. $a^{\frac{1}{3}}$
2. $b^{\frac{1}{5}}$
3. $c^{\frac{5}{3}}$

En los siguientes ejercicios, simplifique.

Ejemplo$\PageIndex{77}$

1. $16^{\frac{3}{2}}$
2. $8^{\frac{2}{3}}$
3. $10,000^{\frac{3}{4}}$

Ejemplo$\PageIndex{78}$

1. $1000^{\frac{2}{3}}$
2. $25^{\frac{3}{2}}$
3. $32^{\frac{3}{5}}$

Contestar

1. 100
2. 125
3. 8

Ejemplo$\PageIndex{79}$

1. $275^{\frac{3}{2}}$
2. $16^{\frac{5}{4}}$
3. $32^{\frac{2}{5}}$

Ejemplo$\PageIndex{80}$

1. $16^{\frac{3}{2}}$
2. $125^{\frac{5}{3}}$
3. $64^{\frac{4}{3}}$

Contestar

1. 64
2. 3125
3. 256

Ejemplo$\PageIndex{81}$

1. $32^{\frac{2}{5}}$
2. $27^{−\frac{2}{3}}$
3. $25^{−\frac{3}{2}}$

Ejemplo$\PageIndex{82}$

1. $64^{\frac{5}{2}}$
2. $81^{−\frac{3}{2}}$
3. $27^{−\frac{4}{3}}$

Contestar

1. 32,768
2. $\frac{1}{729}$
3. $\frac{1}{81}$

Ejemplo$\PageIndex{83}$

1. $25^{\frac{3}{2}}$
2. $9^{−\frac{3}{2}}$
3. $(−64)^{\frac{2}{3}}$

Ejemplo$\PageIndex{84}$

1. $100^{\frac{3}{2}}$
2. $49^{−\frac{5}{2}}$
3. $(−100)^{\frac{3}{2}}$

Contestar

1. 1000
2. $\frac{1}{16,807}$
3. no es un verdadero numbe

Ejemplo$\PageIndex{85}$

1. $−9^{\frac{3}{2}}$
2. $−9^{−\frac{3}{2}}$
3. $(−9)^{\frac{3}{2}}$

Ejemplo$\PageIndex{86}$

1. $−64^{\frac{3}{2}}$
2. $−64^{−\frac{3}{2}}$
3. $(−64)^{\frac{3}{2}}$

Responder

1. −512
2. $−\frac{1}{512}$
3. no es un número real

Ejemplo$\PageIndex{87}$

1. $−100^{\frac{3}{2}}$
2. $−100^{−\frac{3}{2}}$
3. $(−100)^{\frac{3}{2}}$

Ejemplo$\PageIndex{88}$

1. $−49^{\frac{3}{2}}$
2. $−49^{−\frac{3}{2}}$
3. $(−49)^{\frac{3}{2}}$

Responder

1. −343
2. $−\frac{1}{343}$
3. no es un número real

Utilice las leyes de los exponentes para simplificar las expresiones con exponentes racionales

En los siguientes ejercicios, simplifique.

Ejemplo$\PageIndex{89}$

1. $4^{\frac{5}{8}}·4^{\frac{11}{8}}$
2. $m^{\frac{7}{12}}·m^{\frac{17}{12}}$
3. $p^{\frac{3}{7}}·p^{\frac{18}{7}}$

Ejemplo$\PageIndex{90}$

1. $6^{\frac{5}{2}}·6^{\frac{12}{6}}$
2. $n^{\frac{2}{10}}·n^{\frac{8}{10}}$
3. $q^{\frac{2}{5}}·q^{\frac{13}{5}}$

Responder

1. 216
2. n
3. $q^3$

Ejemplo$\PageIndex{91}$

1. $5^{\frac{1}{2}}·5^{\frac{7}{2}}$
2. $c^{\frac{3}{4}}·c^{\frac{9}{4}}$
3. $d^{\frac{3}{5}}·d^{\frac{2}{5}}$

Ejemplo$\PageIndex{92}$

1. $10^{\frac{1}{3}}·10^{\frac{5}{3}}$
2. $x^{\frac{5}{6}}·x^{\frac{7}{6}}$
3. $y^{\frac{11}{8}}·y^{\frac{21}{8}}$

Responder

1. 100
2. $x^2$
3. $y^4$

Ejemplo$\PageIndex{93}$

1. $(m^6)^{\frac{5}{2}}$
2. $(n^9)^{\frac{4}{3}}$
3. $(p^{12})^{\frac{3}{4}}$

Ejemplo$\PageIndex{94}$

1. $(a^{12})^{\frac{1}{6}}$
2. $(b^{15})^{\frac{3}{5}}$
3. $(c^{11})^{\frac{1}{11}}$

Responder

1. $a^2$
2. $b^9$
3. c

Ejemplo$\PageIndex{95}$

1. $(x^{12})^{\frac{2}{3}}$
2. $(y^{20})^{\frac{2}{5}}$
3. $(z^{16})^{\frac{1}{16}}$

Ejemplo$\PageIndex{96}$

1. $(h^6)^{\frac{4}{3}}$
2. $(k^{12})^{\frac{3}{4}}$
3. $(j^{10})^{\frac{7}{5}}$

Responder

1. $h^8$
2. $k^9$
3. $j^{14}$

Ejemplo$\PageIndex{97}$

1. $\frac{x^{\frac{7}{2}}}{x^{\frac{5}{2}}}$
2. $\frac{y^{\frac{5}{2}}}{y^{\frac{1}{2}}}$
3. $\frac{r^{\frac{4}{5}}}{r^{\frac{9}{5}}}$

Ejemplo$\PageIndex{98}$

1. $\frac{s^{\frac{11}{5}}}{s^{\frac{6}{5}}}$
2. $\frac{z^{\frac{7}{3}}}{z^{\frac{1}{3}}}$
3. $\frac{w^{\frac{2}{7}}}{w^{\frac{9}{7}}}$

Responder

1. s
2. $z^2$
3. $\frac{1}{w}$

Ejemplo$\PageIndex{99}$

1. $\frac{t^{\frac{12}{5}}}{t^{\frac{7}{5}}}$
2. $\frac{x^{\frac{3}{2}}}{x^{\frac{1}{2}}}$
3. $\frac{m^{\frac{13}{8}}}{m^{\frac{5}{8}}}$

Ejemplo$\PageIndex{100}$

1. $\frac{u^{\frac{13}{9}}}{u^{\frac{4}{9}}}$
2. $\frac{r^{\frac{15}{7}}}{r^{\frac{8}{7}}}$
3. $\frac{n^{\frac{3}{5}}}{n^{\frac{8}{5}}}$

Responder

1. u
2. r
3. $\frac{1}{n}$

Ejemplo$\PageIndex{101}$

1. $(9p^{\frac{2}{3}})^{\frac{5}{2}}$
2. $(27q^{\frac{3}{2}})^{\frac{4}{3}}$

Ejemplo$\PageIndex{102}$

1. $(81r^{\frac{4}{5}})^{\frac{1}{4}}$
2. $(64s^{\frac{3}{7}})^{\frac{1}{6}}$

Responder

1. $3r^{\frac{1}{5}}$
2. $2s^{\frac{1}{14}}$

Ejemplo$\PageIndex{103}$

1. $(16u^{\frac{1}{3}})^{\frac{3}{4}}$
2. $(100v^{\frac{2}{5}})^{\frac{3}{2}}$

Ejemplo$\PageIndex{104}$

1. $(27m^{\frac{3}{4}})^{\frac{2}{3}}$
2. $(625n^{\frac{8}{3}})^{\frac{3}{4}}$

Responder

1. $9m^{\frac{1}{2}}$
2. $125n^2$

Ejemplo$\PageIndex{105}$

1. $(x^{8}y^{10})^{\frac{1}{2}}$
2. $(a^{9}by ^{12})^{\frac{1}{3}}$

Ejemplo$\PageIndex{106}$

1. $(r^{8}s^{4})^{\frac{1}{4}}$
2. $(u^{15}v^{20})^{\frac{1}{5}}$

Responder

1. $r^{2}s$
2. $u^{3}v^{4}$

Ejemplo$\PageIndex{107}$

1. $(a^{6}b^{16})^{\frac{1}{2}}$
2. $(j^{9}k^{6})^{\frac{2}{3}}$

Ejemplo$\PageIndex{108}$

1. $(r^{16}s^{10})^{\frac{1}{2}}$
2. $(u^{10}v^5)^{\frac{4}{5}}$

Responder

1. $r^{8}s^{5}$
2. $u^{8}v^{4}$

Ejemplo$\PageIndex{109}$

1. $\frac{r^{\frac{5}{2}}·r^{−\frac{1}{2}}}{r^{−\frac{3}{2}}}$
2. $\frac{s^{\frac{1}{5}}·s}{s^{−\frac{9}{5}}}$

Ejemplo$\PageIndex{110}$

1. $\frac{a^{\frac{3}{4}}·a^{−\frac{1}{4}}}{a^{−\frac{10}{4}}}$
2. $\frac{b^{\frac{2}{3}}·b}{b^{−\frac{7}{3}}}$

Responder

1. $a^3$
2. $b^4$

Ejemplo$\PageIndex{111}$

1. $\frac{c^{\frac{5}{3}}·c^{−\frac{1}{3}}}{c^{−\frac{2}{3}}}$
2. $\frac{d^{\frac{3}{5}}·d}{d^{−\frac{2}{5}}}$

Ejemplo$\PageIndex{112}$

1. $\frac{m^{\frac{7}{4}}·m^{−\frac{5}{4}}}{m^{−\frac{2}{4}}}$
2. $\frac{n^{\frac{3}{7}}·n}{n^{−\frac{4}{7}}}$

Responder

1. m
2. $n^2$

Ejemplo$\PageIndex{113}$

$4^{\frac{5}{2}}·4^{\frac{1}{2}}$

Ejemplo$\PageIndex{114}$

$n^{\frac{2}{6}}·n^{\frac{4}{6}}$

Responder

n

Ejemplo$\PageIndex{115}$

$(a^24)^ {\frac{1}{6}}$

Ejemplo$\PageIndex{116}$

$(b^{10})^{\frac{3}{5}}$

Responder

$b^6$

Ejemplo$\PageIndex{117}$

$\frac{w^{\frac{2}{5}}}{w^{\frac{7}{5}}}$

Ejemplo$\PageIndex{118}$

$\frac{z^{\frac{2}{3}}}{z^{\frac{8}{3}}}$

Responder

$\frac{1}{z^2}$

Ejemplo$\PageIndex{119}$

$(27r^{\frac{3}{5}})^{\frac{1}{3}}$

Ejemplo$\PageIndex{120}$

$(64s^{\frac{3}{5}})^{\frac{1}{6}}$

Responder

$2s^{\frac{1}{10}}$

Ejemplo$\PageIndex{121}$

$(r^{9}s^{12})^{\frac{1}{3}}$

Ejemplo$\PageIndex{122}$

$(u^{12}v^{18})^{\frac{1}{6}}$

Responder

$u^{2}v^{3}$

Matemáticas cotidianas

Ejemplo$\PageIndex{123}$

Paisajismo Joe quiere tener una parcela ajardinada cuadrada en su patio trasero. Tiene suficiente compost para cubrir un área de 144 pies cuadrados. Simplifica$144^{\frac{1}{2}}$ para encontrar la longitud de cada lado de su jardín.

Ejemplo$\PageIndex{124}$

Paisajismo Elliott quiere hacer un patio cuadrado en su patio. Tiene suficiente concreto para pavimentar una superficie de 242 pies cuadrados. Simplifica$242^{\frac{1}{2}}$ para encontrar la longitud de cada lado de su patio.Redondea a la décima de pie más cercana.

Responder

15.6 pies

Ejemplo$\PageIndex{125}$

Gravedad Mientras colocaba decoraciones navideñas, Bob dejó caer una decoración desde la parte superior de un árbol que mide 12 pies de altura. Simplifica$\frac{12^{\frac{1}{2}}}{16^{\frac{1}{2}}}$ para encontrar cuántos segundos tardó en que la decoración llegara al suelo. Redondear a la décima de segundo más cercana.

Ejemplo$\PageIndex{126}$

Gravedad Un avión lanzó una bengala desde una altura de 1024 pies sobre un lago. Simplifica$\frac{1024^{\frac{1}{2}}}{16^{\frac{1}{2}}}$ para encontrar cuántos segundos tardó en llegar al agua la llamarada.

Responder

8 segundos

Ejercicios de escritura

Ejemplo$\PageIndex{127}$

Mostrar dos métodos algebraicos diferentes para simplificar$4^{\frac{3}{2}}$. Explica todos tus pasos.

Ejemplo$\PageIndex{128}$

Explique por qué la expresión$(−16)^{\frac{3}{2}}$ no puede ser evaluada.