3.1: Aplicaciones Exponenciales y Logísticas

Última actualización
Guardar como PDF

Page ID: 112002

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hay una variedad de diferentes tipos de relaciones matemáticas. La relación matemática más simple es la relación aditiva. Esta es una situación en la que el valor de una cantidad es siempre una cierta cantidad más (o menor) que otra cantidad. Un buen ejemplo de una relación aditiva es una relación de edad. En una relación de edad, la edad de la persona mayor es siempre la misma cantidad más que la edad de la persona más joven. Si la persona mayor es cinco años mayor, entonces la edad de la persona mayor ($y$) siempre será igual a la edad de la persona más joven$(x)$ más cinco:$y=x+5$

Se observa otro tipo de relación aditiva donde dos cantidades suman un valor constante. Digamos que hay una tabla cuya longitud es de 20 pulgadas. Si la cortamos en dos piezas, siendo una pieza de 6 pulgadas, entonces la otra pieza será de 14 pulgadas. Si una pieza mide 9 pulgadas, entonces la otra será de 11 pulgadas. Si una pieza es$x$ pulgadas, entonces la otra pieza$(y)$ será$20-x: y=20-x$ o$x+y=20$

El siguiente tipo de relación matemáticaHP es una relación multiplicativa. Esto representa una situación en la que una cantidad es siempre un múltiplo de la otra cantidad. Esto se ve comúnmente en las relaciones proporcionales. Si una receta para un pastel requiere 2 tazas de harina, entonces, si queremos hacer 3 pasteles, necesitaremos 6 tazas de harina. La cantidad de harina$(y)$ es siempre dos veces la cantidad de pasteles que queremos hacer$(x): y=2 x$

Si una receta para un lote de galletas (con 20 galletas por lote) requiere 1.5 tazas de azúcar, entonces tres lotes requerirían 4.5 tazas de azúcar. La cantidad de azúcar requerida ($y$) es siempre el número de lotes$(x)$ veces$1.5: y=1.5 x$. Si quisiéramos representar esta relación en función del número de cookies en lugar del número de lotes, necesitaríamos ajustar la fórmula. Dado que hay 20 galletas por lote, podríamos ajustar nuestra fórmula para que primero calculemos el número de lotes a partir del número de galletas y luego multipliquemos por$1.5 .$ Si el número de galletas es$x$ y la cantidad de azúcar es$y,$ entonces$y=1.5 * \frac{x}{20}$ o$y=\frac{3}{40} x$
La siguiente tipo de relación matemática es la relación polinómica. En este tipo de relación, una cantidad está relacionada con un poder de otra cantidad. Un buen ejemplo de este tipo de relación implica la gravedad. Como descubrió Galileo en el siglo XVI, la distancia que cae un objeto después de caer no es proporcional al tiempo que ha estado cayendo. Más bien, es proporcional al cuadrado de la época. La siguiente tabla muestra este tipo de relación.
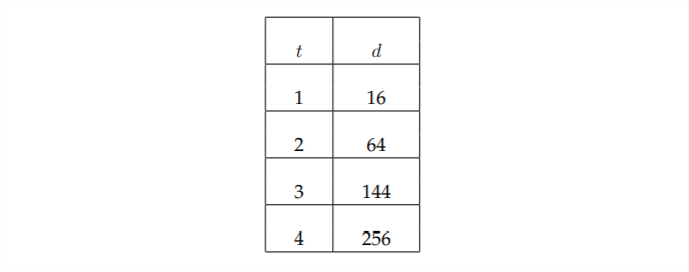
$clipboard_e72a9e6e53cc72000e31135223fb34bc9.png$
Después de un segundo, parece que la distancia siempre será dieciséis veces el tiempo que el objeto ha estado cayendo. No obstante, después de dos segundos, podemos ver que esta relación ya no es cierta. Eso es porque esta relación es una relación polinómica en la que la distancia que ha caído un objeto ($d$) es proporcional al cuadrado del tiempo que ha estado cayendo$(t): d=16 t^{2}$

Relaciones exponenciales
El siguiente tipo de relación es el foco de este capítulo: la relación exponencial. En esta situación, la tasa de cambio de una cantidad es proporcional al tamaño de esa cantidad. Esta relación se puede explorar con más profundidad en un curso de cálculo integral, pero aquí discutiremos los conceptos básicos.

En una relación lineal o proporcional, la pendiente, o tasa de cambio, es constante. Por ejemplo, en la ecuación$y=3 x+1,$ la pendiente es siempre tres, sin importar cuáles sean los valores de$x$ y$y$ sean. En una relación exponencial, la tasa de cambio (también llamada "$y$prime” o$y^{\prime}$) es proporcional al valor de$y .$ En este caso, decimos que
\ [
y^ {\ prime} =k * y
\]
Esto es lo que se conoce como una ecuación diferencial. Esta es una ecuación en la que se relacionan la variable y su tasa de cambio. A través de los procesos de cálculo diferencial e integral, podemos resolver la ecuación anterior$y^{\prime}=k * y$ como:
\ [
y=A e^ {k t}
\]
En la ecuación anterior,$A$ es el valor de$y$ en el tiempo$t=0, k$ es una constante que determina cómo rápido la cantidad$y$ aumenta o disminuye y$t$ juega el papel de la variable independiente (como$x$ suele hacer) y representa el tiempo que ha pasado. Si$k$ es positivo, entonces la cantidad$y$ está creciendo porque su tasa de cambio es positiva. Si$k$ es negativo, entonces la cantidad$y$ está disminuyendo porque la tasa de cambio es negativa.

La cantidad representada por$e$ en la ecuación anterior es una constante matemática (like$\pi$) que a menudo se usa para representar relaciones exponenciales. La mejor manera de entender el valor$e$ y lo que representa está directamente relacionada con preguntas fundamentales a partir del cálculo diferencial e integral.

El cálculo diferencial se ocupa principalmente de la cuestión de las pendientes. Se discutió anteriormente que una relación lineal tiene una pendiente constante. Las relaciones polinomiales y exponenciales tienen pendientes que dependen del valor de$x$ y/o$y$. Esto es lo que los hace curvas más que líneas. Si consideramos las pendientes de algunas relaciones exponenciales diferentes, podemos ver un aspecto de donde$e$ viene el valor para.

Consideremos las gráficas de las siguientes relaciones:

\ [\ begin {aligned}
y &=1.5^ {x}\\
y &=2^ {x}\\
y &=3^ {x}\\
y &=10^ {x}

\ end {alineado}\]
Veamos el gráficas para estas funciones:
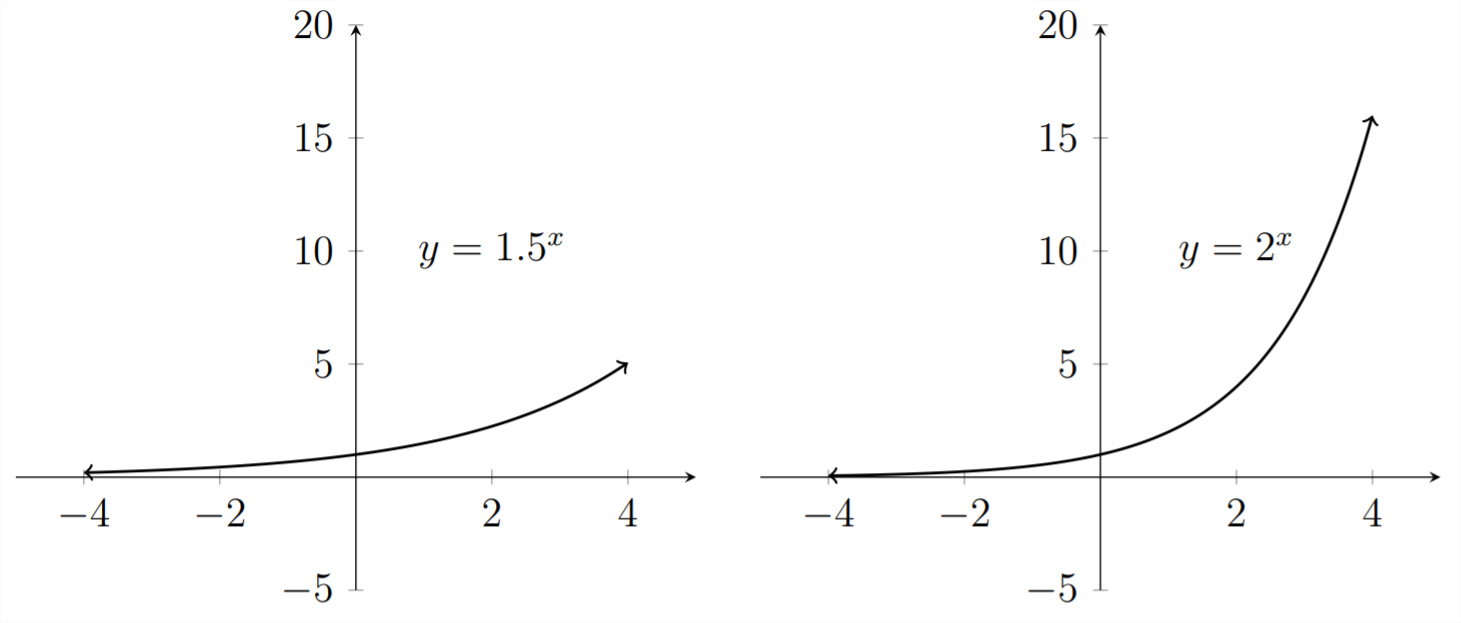
$clipboard_e0585237f45cd9b5466c6e014dcce1502.png$
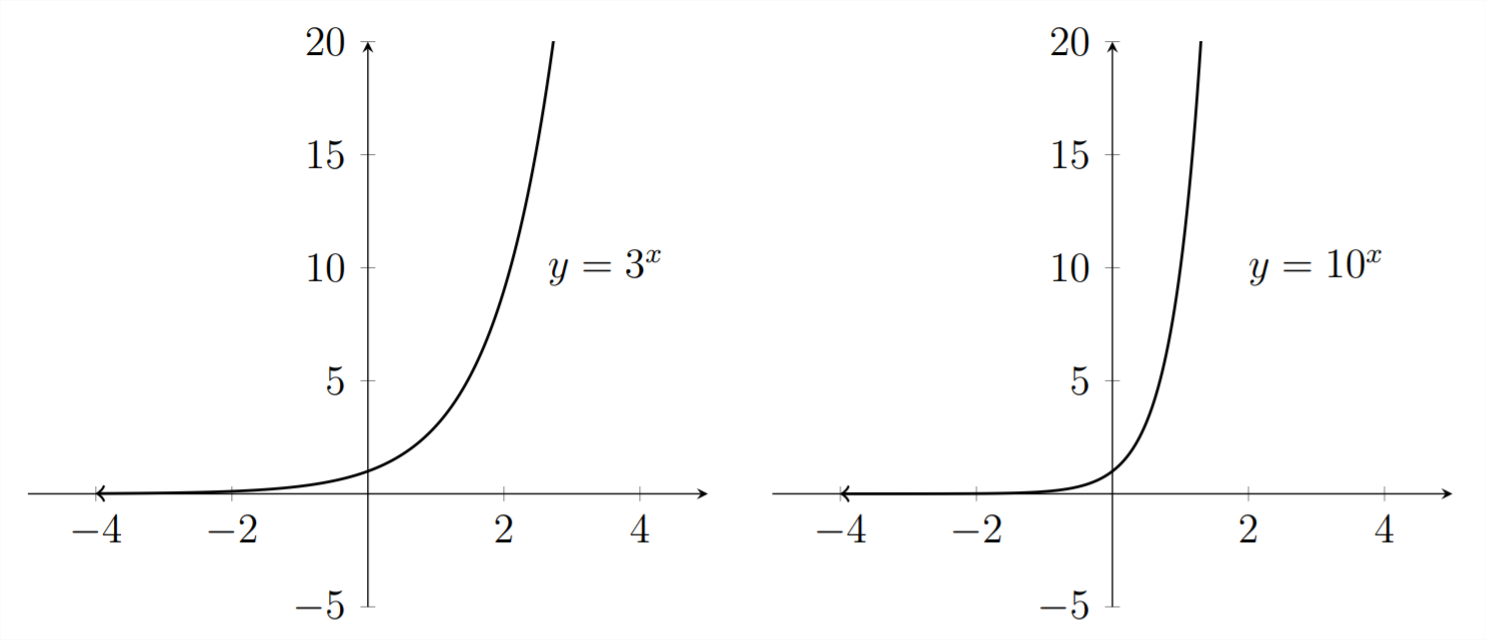
$clipboard_e5cd662884ffe22983e49d65666da6d59.png$
Podemos ver que estas gráficas demuestran un comportamiento ligeramente diferente y diferentes$x$ y$y$ valores. Una cosa que todos tienen en común es que todos pasan por el punto (0,1) de la gráfica. Esto es porque$1.5^{0}=1,2^{0}=1,3^{0}=1$ y$10^{0}=1 .$ Por lo tanto el punto donde$x$$y$ es 0 y es 1 está en las cuatro gráficas.
Aunque las cuatro gráficas pasan por el punto$(0,1),$, cada una hace esto de una manera diferente. Veamos la pendiente de una línea tangente a cada curva en el punto$(0,1) .$ Esta es la línea recta que toca la curva en el punto$(0,1),$ pero en ninguna otra parte:
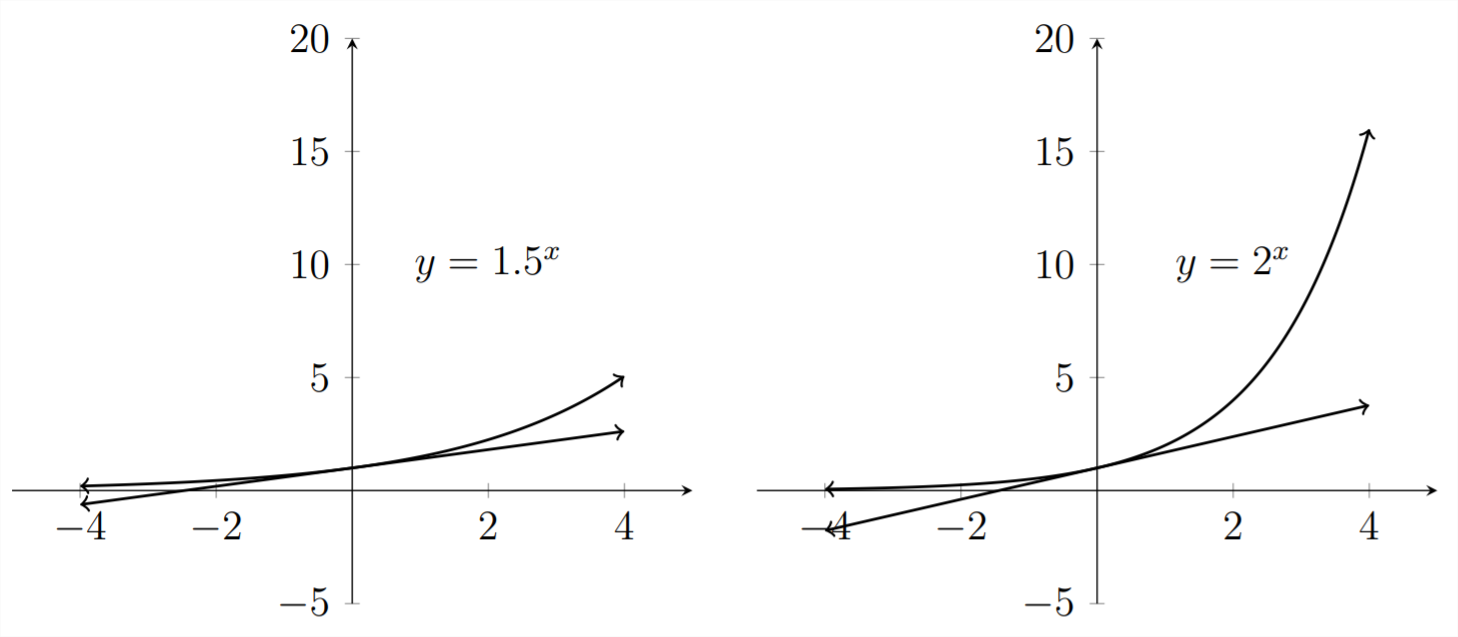
$clipboard_ed2b3e2a5399e939277aefac06ac2166d.png$
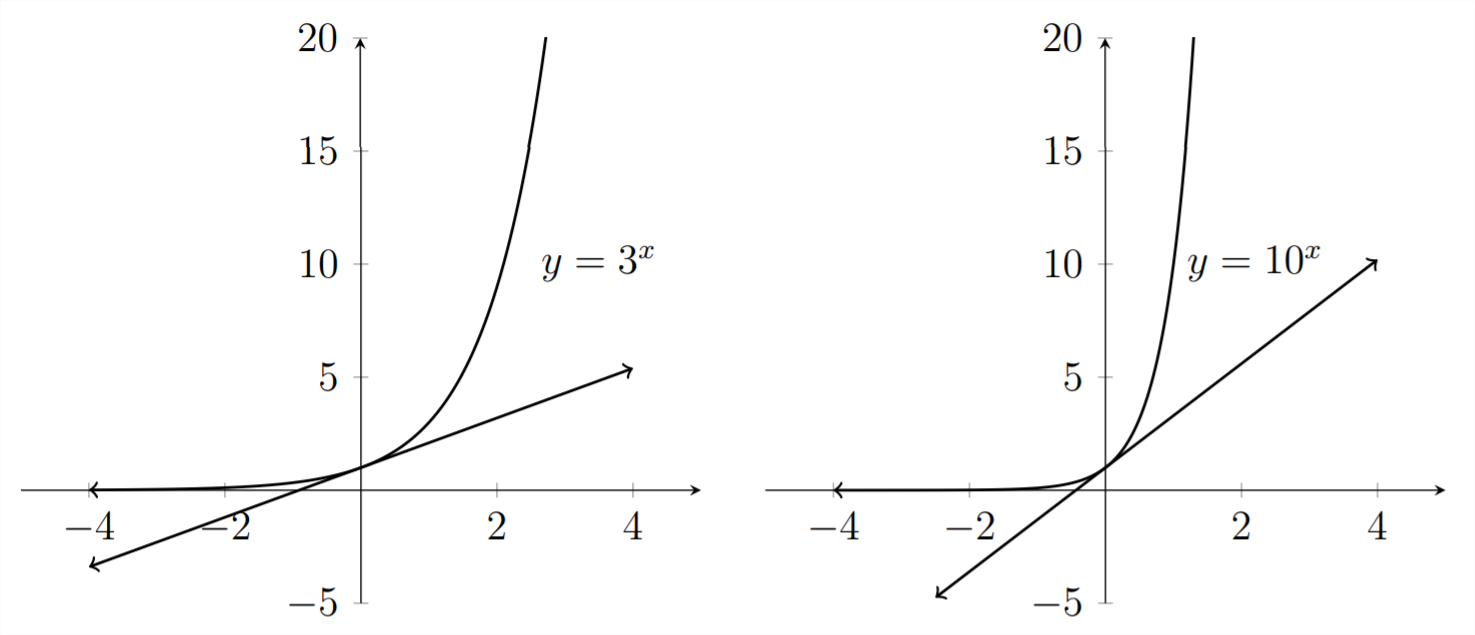
$clipboard_e3cdedf0efda0aae1a5fb497e17d13501.png$
Podemos ver que las pendientes de estas líneas tangentes son todas diferente. En el caso de$y=2^{x},$ la pendiente de la línea tangente en (0,1) es aproximadamente$0.7,$ mientras que para la gráfica de$y=3^{x},$ la pendiente de la línea tangente en (0,1) es aproximadamente 1.1

A medida que los matemáticos examinaron estas gráficas durante los siglos XVII y XVIII, comenzaron a cuestionarse cuál era el valor de la base "$b^{\prime \prime}$debería estar en la ecuación$y=b^{x}$ para que la pendiente de la línea tangente en el punto (0,1) fuera igual a exactamente$1 .$ La respuesta fue$e \approx 2.71828$

Otra forma de derivar el valor de$e$ usos Cálculo Integral. Cálculo Integral a menudo se ocupa de encontrar el área bajo una curva. Este proceso puede generalizarse y utilizarse para realizar muchos otros tipos de cálculos que son similares a encontrar área.
Considerar la gráfica de la curva$y=\frac{1}{x}$
$clipboard_e9a186b91477d96e879498c92914d344f.png$
Podemos delinear bordes sobre los$x$ valores y determinar el área de la región resultante utilizando las técnicas de cálculo:
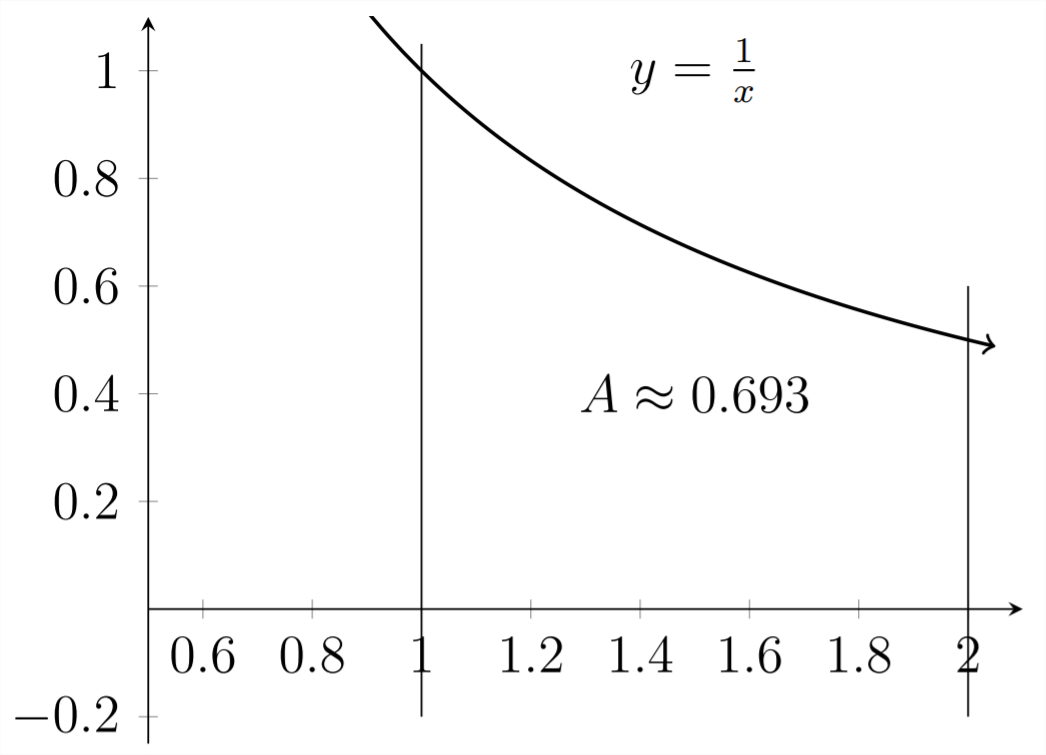
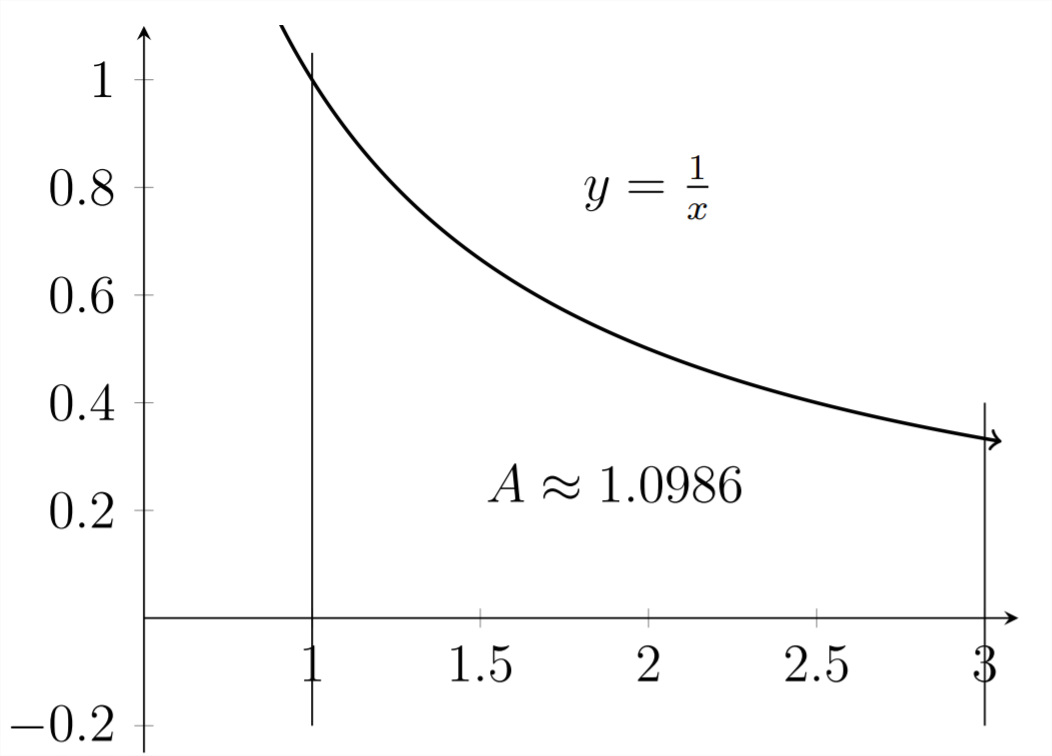
$clipboard_e2ccf7ca26a565916a9c1499bee832455.png$ $clipboard_e2c0f8eb4845651434e020c1018e720f0.png$
Estos valores para el área bajo la curva son en realidad los mismos valores que los de la pendiente de la línea tangente en las gráficas anteriores. Si haces la pregunta, “¿Dónde deberías dibujar la segunda línea vertical para que el área bajo la curva sea igual a exactamente$1 ?^{\prime \prime}$ entonces al igual que la pregunta de pendiente, la respuesta es$e \approx 2.71828$
Así es como$e$ se determinó el valor de y por qué se usa para representar estos relaciones exponenciales.

Relaciones logísticas
Consideremos la gráfica de$y=2^{x}:$
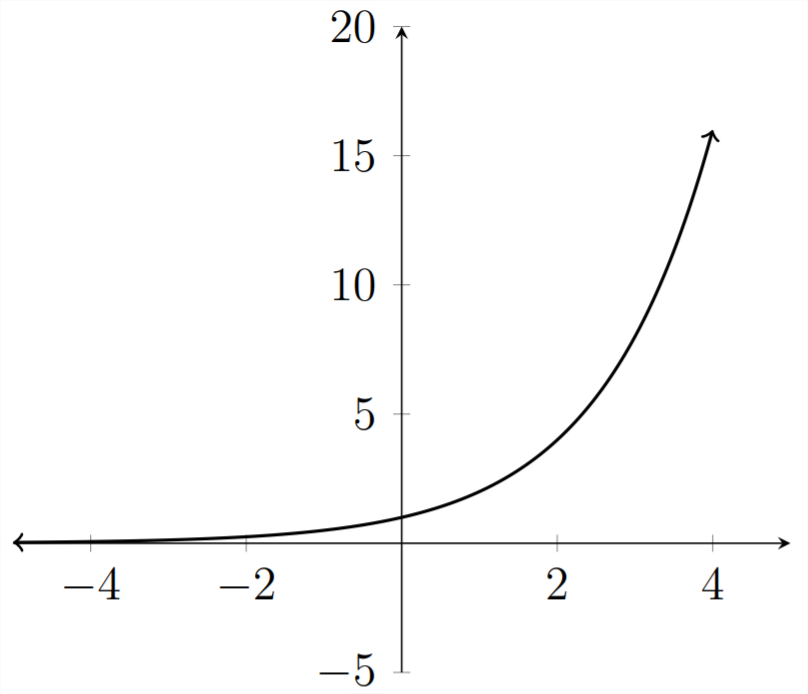
$clipboard_ea4ac62601b268f01d12f5c328fcb9d7d.png$
Si extendemos el$x$ eje -más allá$x=4,$ veríamos que los$y$ valores para esta relación crecerán muy rápidamente, ya que continúan duplicándose.
$clipboard_e0c1c146f3e5e7057ff749cee109c8204.png$

Algunos fenómenos en el mundo natural exhiben un comportamiento similar al crecimiento de esta función. Sin embargo, en el mundo natural, pocas, si alguna, las cosas pueden crecer sin restricciones. La mayor parte del crecimiento de cualquier tipo está limitado por los recursos que alimentan el crecimiento. Las poblaciones suelen crecer exponencialmente por un periodo de tiempo, sin embargo, las poblaciones dependen de los recursos naturales para continuar creciendo. Como resultado, la función exponencial simple solo es útil para modelar el comportamiento del mundo real si los$x$ valores -son limitados.

Fue este problema con la función exponencial simple lo que llevó al matemático francés Pierre Verhulst a ajustar ligeramente la ecuación diferencial que da lugar a la función exponencial para hacerla más realista.
La ecuación diferencial original decía:
\ [
y^ {\ prime} =k * y
\]
Esto dice que la tasa de crecimiento de siempre$y$ es directamente proporcional al valor de
$y .$ En otras palabras, cuanto más grande obtiene una población, más rápido crecerá - para siempre. Verhulst cambió esto para decir:
\ [
y^ {\ prime} =k * y\ left (1-\ frac {y} {N}\ right)
\]
Esta es la relación definitoria para la función Logística. Observe que cuando los valores de$y$ son pequeños, esto es esencialmente lo mismo que el exponencial simple. Si$y$ es pequeño, entonces el$\left(1-\frac{y}{N}\right)$ término estará muy cerca de 1 y producirá un comportamiento muy parecido al simple exponencial.

El$N$ en la fórmula es una “población máxima” teórica. A medida que el valor de$y$ se acerca a este valor máximo,$\frac{y}{N}$ se acercará a 1 y$\left(1-\frac{y}{N}\right)$ se hará cada vez más pequeño. A medida que se va haciendo más pequeño, el factor de$\left(1-\frac{y}{N}\right)$ ralentizará el crecimiento de la función para modelar la presión que se ejerce sobre los recursos que están impulsando el crecimiento.

La solución de la ecuación logística es bastante complicada y da como resultado una forma estándar de:
\ [
y=\ frac {N} {1+b e^ {-k t}}
\]

A continuación se muestra la gráfica para una relación logística
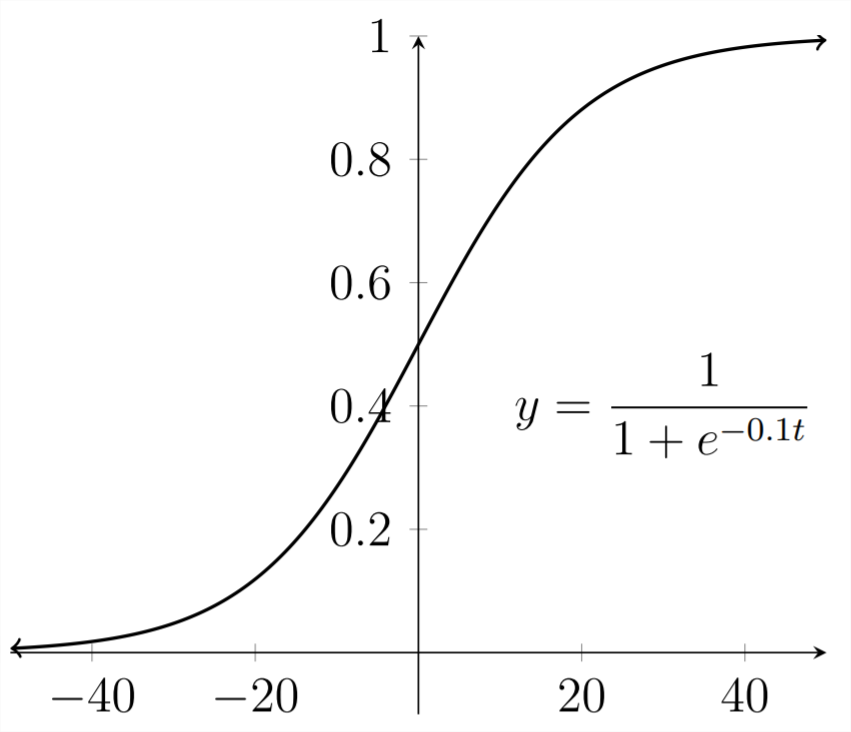
$clipboard_ef707107b9fd89d7edbe403835b7171ab.png$
muestral: La forma “lazy-s” es característica de la función logística. En las primeras etapas, la relación muestra un crecimiento muy similar a la función exponencial simple pero, a medida que la función crece, el crecimiento disminuye y los valores de la función se estabilizan. El$y$ valor máximo de$N$ es siempre la asíntota horizontal para la función logística.

Relaciones Exponenciales Negativas
La función Logística es muy útil para modelar fenómenos del mundo natural. Aunque la función exponencial simple es algo limitada en el modelado de fenómenos naturales, la exponencial negativa es bastante útil. Mirando hacia atrás a la gráfica de$y=2^{x}$:
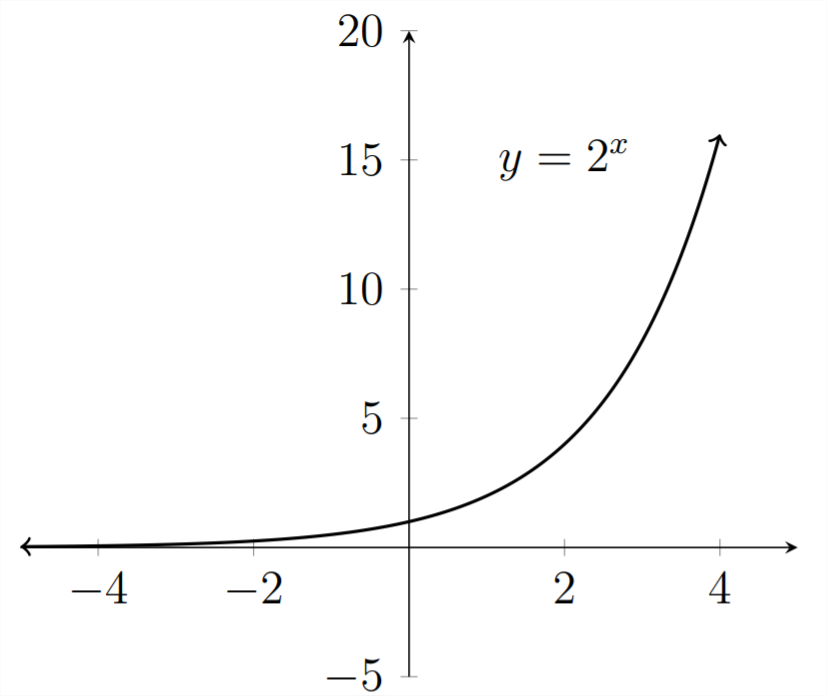
$clipboard_ee36999948f37dea72536272098f913e4.png$
Si damos la vuelta a la gráfica cambiando$x$ a$-x$ en la fórmula, entonces estaremos trabajando con la cola en descomposición de la gráfica:
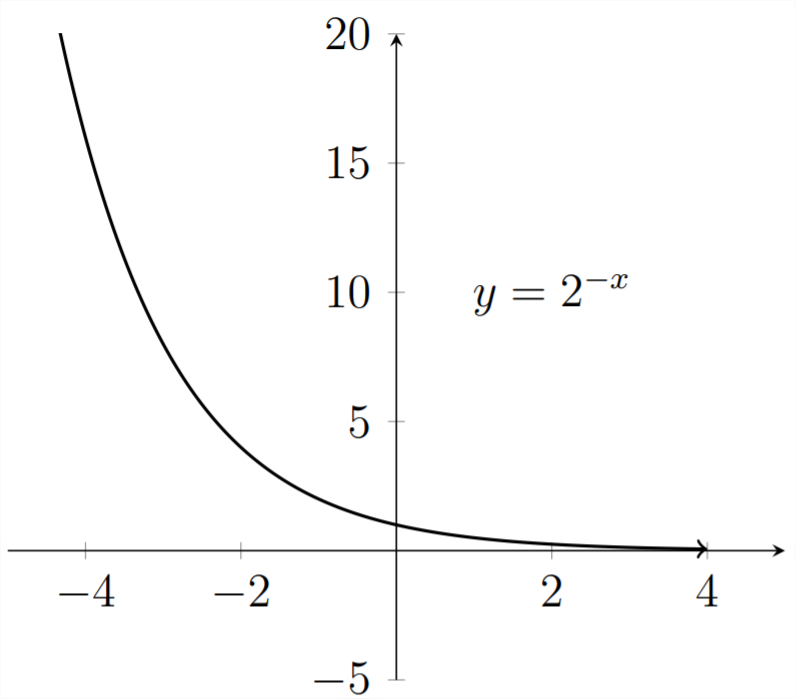
$clipboard_e64be42f0e8ad9b061a70dff783d638c3.png$
Vamos a acercar la porción de la gráfica en el Cuadrante I:
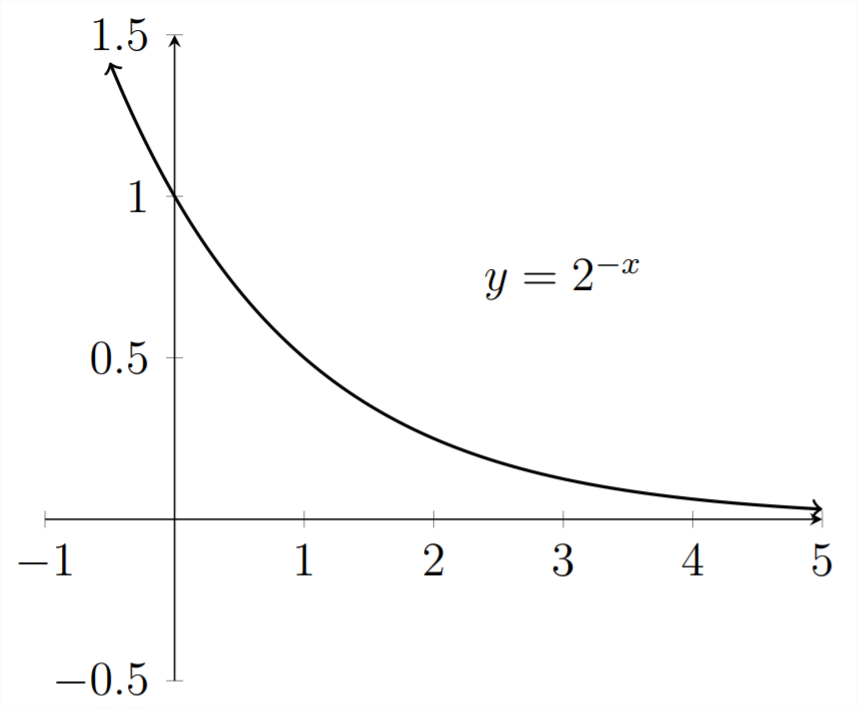
$clipboard_ecdebe00c1d293896d59dbfb6cf7fa12f.png$
El comportamiento mostrado en la gráfica es bastante útil para modelar la desintegración radiactiva, procesos de calentamiento y enfriamiento, y asimilación de medicamentos en el torrente sanguíneo. Veamos un ejemplo.

Ejemplo
Si a un paciente se le inyectan 150 microgramos de medicamento, la cantidad de medicamento que aún se encuentra en el torrente sanguíneo después de$t$ horas viene dada por la función:
\ [
A (t) =150 e^ {-0.12 t}
\]
a) Encuentra la cantidad de medicación en el torrente sanguíneo después de 3 horas.
Redondee su respuesta a las 100 th más cercanas.
b) ¿Cuánto tiempo tardará la cantidad de medicamento en llegar a los 60 microgramos?
Redondee su respuesta a las 10 de hora más cercanas.

En esta sección nos enfocaremos en resolver estos problemas utilizando la calculadora gráfica. En secciones posteriores, cubriremos procesos que pueden ser utilizados para resolver estos problemas algebraicamente. Es útil entender ambos métodos de solución.
Primero, graficemos la función dada en el problema:
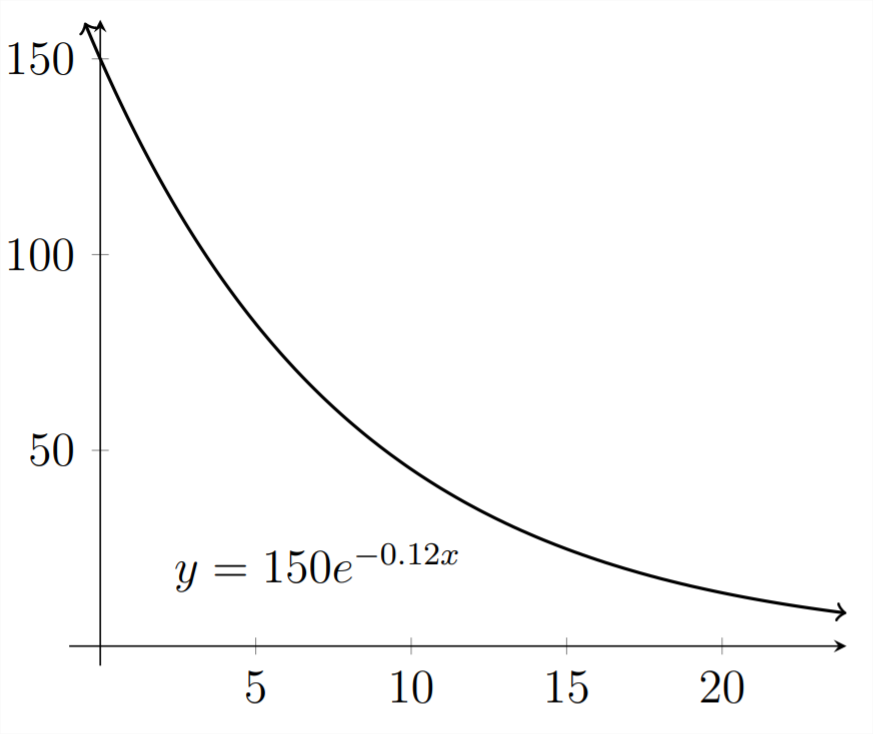
$clipboard_eb4c30181e97094f8ae176988f2a24d50.png$
Podemos calcular directamente la respuesta para la parte
(a) tapando el valor de 3 para$t$ o podemos usar la tabla en la calculadora gráfica para encontrar este valor:
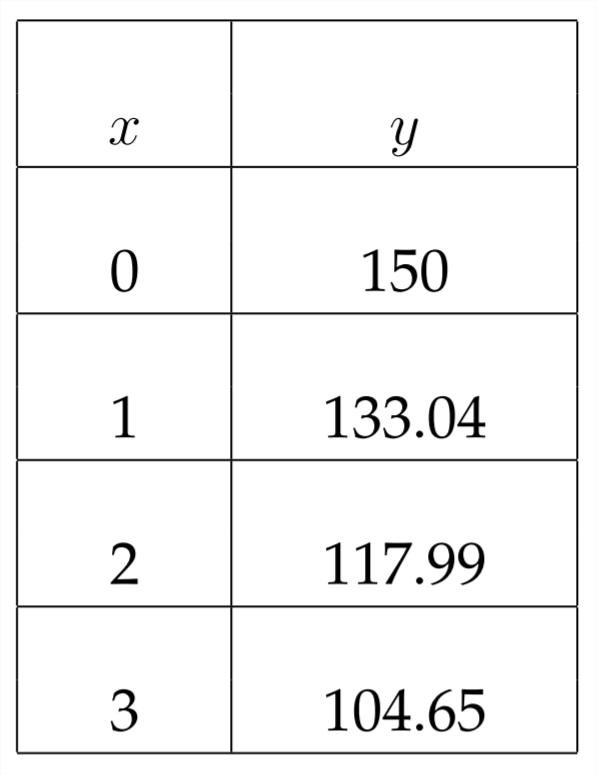
$clipboard_ea6e06323b03e4e6de95f83b997471486.png$

Podemos ver que después de 3 horas hay aproximadamente 104.65 microgramos de medicamento en el torrente sanguíneo del paciente.

Para responder gráficamente a la parte (b), graficaremos la función original junto con la línea horizontal.$y=60 .$ Cuando encontremos la intersección de estas dos gráficas, sabremos cuánto tiempo tarda en haber 60 microgramos de medicamento en el torrente sanguíneo del paciente:
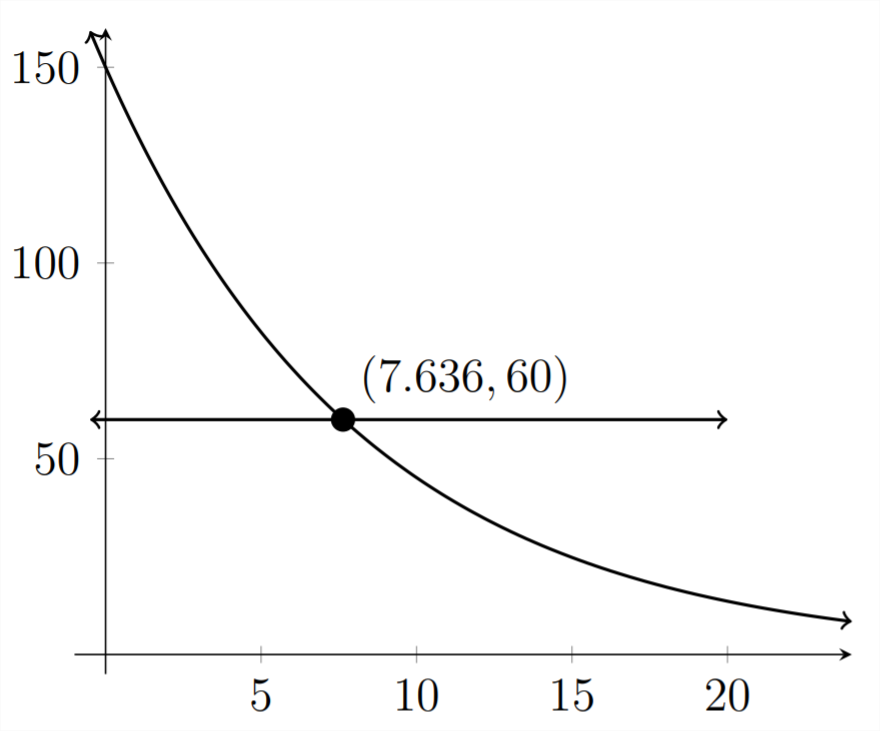
$clipboard_e13212db00ca5d7e9780d73821c397600.png$

Aquí, podemos ver que tardarían alrededor de 7.6 horas (o alrededor de 7 horas 36 minutos), para que haya 60 microgramos de medicamento en el torrente sanguíneo del paciente.

Ejemplo
La población de ciervos en una reserva natural se puede modelar usando la ecuación:
\ [
y=\ frac {8000} {1+9 e^ {-0.2 t}}
\]
$y$ indica el número de venados que viven en la reserva natural y$t$ representa el número de años que han pasado desde que se estableció allí la población inicial de venados.
a) ¿Cuántos venados había en la población inicial?
b) ¿Cuál es la población de venados después de 10 años?
Redondee su respuesta al número entero más cercano.
c) Cuánto tiempo tarda la población en llegar$5,000 ?$
Redondea tu respuesta al 10 º del año más cercano.
Las partes
(a) y (b) pueden ser respondidas a partir de una tabla de valores para la función. Antes de mirar la mesa, consideremos la pregunta en la Parte (a). El problema es preguntar cuál era la población inicial de venados. El significa que estamos buscando averiguar qué$y$ es cuando$t=0$
veamos qué pasa cuando conectamos cero adentro para$t$ en la fórmula:
\ [
\ begin {aligned}
y &=\ frac {8000} {1+9 e^ {-0.2 * 0}} =\ frac {8000} {1+9 e^ {0}}\\
&=\ frac {8000} {1+9 * 1} =\ frac {8000} {10}\\
&=800
\ end {alineado}
\]

Veamos la tabla de valores:
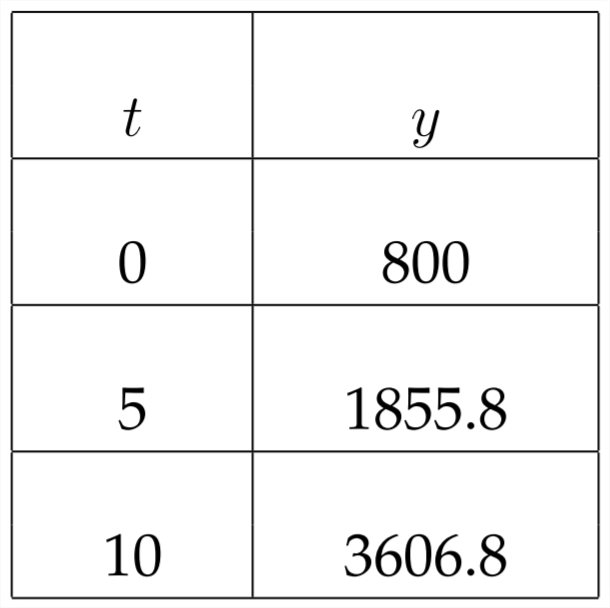
$clipboard_e70905c758108b69be05eece038c280f4.png$
Al número entero más cercano, la población de venados después de 10 años es de 3,607
En la Parte (c), necesitaremos graficar una línea horizontal en$y=5,000$ y encontrar la intersección.
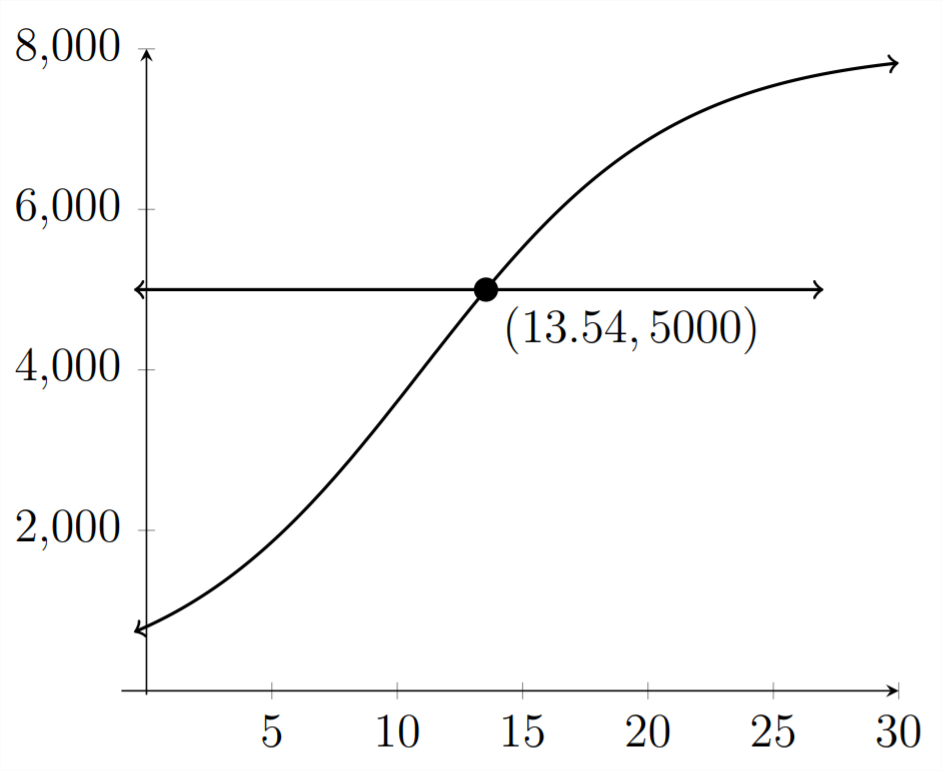
$clipboard_e6c7402918fad38d885623e9eb10f8d11.png$

A la 10 más cercana, la población de ciervos tarda unos 13.5 años en llegar a 5,000

Ejercicios 3.1
1) Medicación en el torrente sanguíneo
La función$A(t)=200 e^{-0.014 t}$ da la cantidad de medicamento, en miligramos, en el torrente sanguíneo de un paciente$t$ minutos después de que se haya inyectado el medicamento.
a) Encontrar la cantidad de medicamento en el torrente sanguíneo después de 45 minutos.
Redondee su respuesta al miligramo más cercano.
b) ¿Cuánto tiempo tardará la cantidad de medicamento en llegar a los 50 miligramos?
Redondee su respuesta al minuto más cercano.

2) Medicación en el torrente sanguíneo
La función$D(t)=50 e^{-0.2 t}$ da la cantidad de medicamento, en miligramos, en el torrente sanguíneo de un paciente$t$ horas después de que se haya inyectado el medicamento.
a) Encontrar la cantidad de medicamento en el torrente sanguíneo después de 3 horas.
Redondee su respuesta al miligramo más cercano.
b) ¿Cuánto tiempo tardará la cantidad de medicamento en llegar a los 10 miligramos?
Redondee su respuesta al minuto más cercano.

3) Población de peces
El número de lubina en un lago se puede modelar usando la ecuación dada:
\ [
P (t) =\ frac {3600} {1+7 e^ {-0.05 t}}
\]
donde$t$ está el número de meses que han pasado desde que el lago fue abastecido de lubina. En cada pregunta a continuación, redondee su respuesta al número entero más cercano.
a) ¿Cuántos lubinos había en el lago inmediatamente después de que se abasteciera?
b) ¿Cuántos lubinos había en el lago 1 año después de que se abasteciera?

4) Población de aves
La población de una determinada especie de ave está limitada por el tipo de hábitat requerido para la anidación. La población puede modelarse usando la siguiente ecuación:
\ [
P (t) =\ frac {5600} {0.5+27.5 e^ {-0.044 t}}
\]
donde$t$ está el número de años. En cada pregunta a continuación, redondee su respuesta al número entero más cercano.
a) Encontrar la población inicial de aves.
b) ¿Cuál es la población 100 años después?

5) Un Modelo de Temperatura
Una taza de café se calienta$180^{\circ} \mathrm{F}$ y se coloca en una habitación que mantiene una temperatura de$65^{\circ} \mathrm{F}$. La temperatura del café después de que hayan pasado los$t$ minutos viene dada por:
\ [
F (t) =65+115 e^ {-0.042 t}
\]
a) Encuentra la temperatura del café 10 minutos después de que se coloque en la habitación.
Redondee su respuesta al grado más cercano.
b) ¿Cuándo será la temperatura del café$100^{\circ} \mathrm{F}$?
Redondee su respuesta a la décima de minuto más cercana.

6) Una
Sopa Modelo de Temperatura a una temperatura de$170^{\circ} \mathrm{F}$ se vierte en un recipiente en una habitación que mantiene una temperatura constante. La temperatura de la sopa disminuye según el modelo dado por:
\ [
F (t) =75+95 e^ {-0.12 t}
\]
donde$t$ está el número de minutos que han pasado desde que se vertió la sopa.
a) ¿Cuál es la temperatura de la sopa después de 2 minutos?
Redondee su respuesta al 10 º de grado más cercano.
b) Un determinado cliente prefiere que la sopa se enfríe a$110^{\circ} \mathrm{F}$.
¿Cuánto tardará esto?
Redondee su respuesta al 10 de minuto más cercano.

7) Desintegración radiactiva
Una sustancia radiactiva se descompone de tal manera que la cantidad de masa restante después de$t$ días viene dada por la ecuación:
\ [
m (t) =13 e^ {-0.015 t}
\]
donde la cantidad se mide en kilogramos.
a) Encuentra la misa en el tiempo$t=0$
b) ¿Cuánto de la masa queda después de 45 días?
c) ¿Cuánto tiempo tarda en quedar 5 kg. para que queden 5 kg.?

8) Desintegración
radiactiva El yodo radiactivo es utilizado por los médicos como trazador en el diagnóstico de ciertos trastornos de la glándula tiroides. Este tipo de yodo se descompone de tal manera que la masa que queda después de$t$ días viene dada por:
\ [
m (t) =6 e^ {-0.087 t}
\]
donde la cantidad se mide en gramos.
a) Encuentra la misa en el tiempo$t=0$
b) ¿Cuánto queda después de 20 días?
c) ¿Cuánto tiempo tarda en quedar 2 gramos?
Redondee su respuesta a la décima de día más cercana.

9) Población de peces
La función:
\ [
P (t) =\ frac {12} {1+e^ {-t}}
\]
da el tamaño de una población de peces en miles al tiempo$t,$ medido en años.
a) Encontrar la población inicial de peces a la vez$t=0$
Encuentra la población de peces después de 2 años, tiempo$t=2$
b) ¿Cuánto tiempo tomará para que la población sea$10,000 ?$
¿Cuál parece ser la población máxima para este modelo en particular?

10) Población de peces
La función:
\ [
P (t) =\ frac {70} {1+2 e^ {-t}}
\]
da el tamaño de una población de peces en miles al tiempo$t,$ medido en años.
a) Encontrar la población inicial de peces a la vez$t=0$
Encontrar la población de peces después de 1.5 años,$t=1.5$
b) ¿Cuánto tiempo tomará para que la población sea$50,000 ?$
¿Cuál parece ser la población máxima para este modelo en particular?

11) Población de peces
La función:
\ [
P (t) =\ frac {20} {1-0.4 e^ {-0.35 t}}
\]
da el tamaño de una población de peces en miles al tiempo$t,$ medido en años.
a) Encontrar la población inicial de peces a la vez$t=0$
Encontrar la población de peces después de 5 años, tiempo$t=5$
b) ¿Cuánto tiempo tomará para que la población sea$25,000 ?$
¿Qué le sucede a esta población a lo largo del tiempo?

12) Población de peces
La función:
\ [
P (t) =\ frac {10} {1-0.73 e^ {-0.08 t}}
\]
da el tamaño de una población de peces en miles al tiempo$t,$ medido en años.
a) Encontrar la población inicial de peces a la vez$t=0$
Encontrar la población de peces después de 5 años, tiempo$t=5$
b) ¿Cuánto tiempo tomará para que la población sea$25,000 ?$
¿Qué le sucede a esta población a lo largo del tiempo?

13) Mezcla Continua
Un tanque de 100 galones de agua pura tiene agua salada con 0.5 lb por galón agregado a una tasa de 2 galones por minuto. La solución de salmuera se mezcla a fondo y se drena a razón de 2 galones por minuto.

La ecuación de cuántas libras de sal hay en el tanque a la vez$t$ viene dada por:
\ [
y=50-50 e^ {-0.02 t}
\]
donde$y$ se mide en libras y$t$ se mide en minutos.
a) ¿Cuántas libras de sal hay en el tanque después de 20 minutos?
b) ¿Cuánto tiempo tarda en haber 30 libras de sal en el tanque?
Redondee su respuesta a la décima de minuto más cercana.

14) Mezcla Continua
Un tanque de 20 galones de agua pura tiene agua salada con 0.4 lb por galón de sal agregada a una tasa de 3 galones por minuto. La solución de salmuera se mezcla a fondo y se drena a razón de 3 galones por minuto.

La ecuación de cuántas libras de sal hay en el tanque a la vez$t$ viene dada por:
\ [
y=8-8 e^ {-0.15 t}
\]
donde$y$ se mide en libras y$t$ se mide en minutos.
a) ¿Cuántas libras de sal hay en el tanque después de 15 minutos?
b) ¿Cuánto tiempo tarda en haber 6 libras de sal en el tanque?
Redondee su respuesta a la décima de minuto más cercana.

15) Mezcla Continua
Un tanque contiene 200 galones de una$2 \%$ solución de HCl. Se agrega una$5 \%$ solución de HCl a 5 galones por minuto. La solución bien mezclada se está drenando a 5 galones por minuto.
La cantidad de HCl en el tanque en cualquier momento dado$t$ en minutos es:
\ [
y=10-6 e^ {-0.025 t}
\]
a) ¿Cuántos galones de HCl hay en el tanque a los$t=25$ minutos?
b) Cuándo alcanza la concentración de HCl en la solución$4 \% ?$

16) Mezcla Continua
Un tanque contiene 100 galones de agua salada que contiene un total de 25 lbs de sal. El agua salada que contiene 0.4 lbs por galón se agrega al tanque a una velocidad de 5 galones por minuto y la solución bien mezclada se drena a la misma velocidad.
La cantidad de sal en libras en el tanque en cualquier momento dado$t$ en minutos es:
\ [
y=40-15 e^ {-0.05 t}
\]
a) ¿Cuántas libras de sal hay en el tanque a los$t=20$ minutos?
b) ¿Cuánto tiempo tarda en haber 30 libras de sal en el tanque?