5.1: La Ecuación del Círculo

La ecuación para un círculo se da típicamente como:
\ [(x-h) ^ {2} + (y-k) ^ {2} =r^ {2}
\] En esta ecuación, el punto\((h, k)\) representa el centro del círculo y\(r\) representa el radio del círculo. Esta ecuación se deriva de la fórmula de distancia. La definición de un círculo es el locus (o colección) de puntos que son equidistantes de un punto dado (el centro del círculo).

Entonces, tomando esta definición, podemos decir que cualquier punto\((x, y)\) que esté en el círculo debe estar a una\(r\) distancia del centro. Usando la fórmula de distancia:
\ [d=\ sqrt {\ left (x_ {1} -x_ {2}\ right) ^ {2} +\ left (y_ {1} -y_ {2}\ right) ^ {2}}
\] Cuadrando ambos lados:
\ [d^ {2} =\ left (x_ {1} -x_ {2}\ right) ^ {2} +\ left (y_ {1} -y_ {2}\ right) ^ {2}
\] En esta situación, la distancia\(d\) es el radio de el círculo,\(r .\) Esta distancia debe ser la misma para todos los puntos del círculo. Entonces cualquier punto en el borde del círculo,\((x, y)\) debe estar a una\(r\) distancia del centro del círculo,\((h, k)\)
\ [(x-h) ^ {2} + (y-k) ^ {2} =r^ {2}
\]

Ejercicios\(5.1(a)\)

Determine el centro y el radio para cada círculo y dibuje la gráfica del círculo.
1)\(\quad(x-3)^{2}+(y+1)^{2}=9\)
2)\(\quad(x+4)^{2}+(y+2)^{2}=16\)
3)\(\quad(x-1)^{2}+(y-6)^{2}=20\)
4)\(\quad(x-2)^{2}+(y+5)^{2}=27\)
5)\(\quad(x+7)^{2}+(y-4)^{2}=33\)
6)\(\quad(x-5)^{2}+(y-3)^{2}=50\)

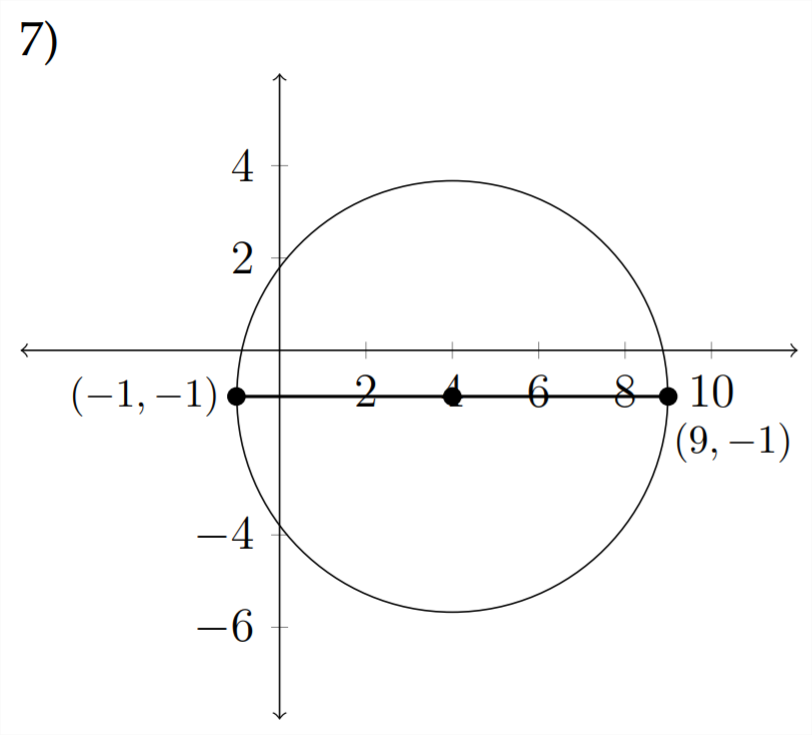
Determinar la ecuación para cada círculo. Cada línea representa un diámetro

A veces la ecuación para un círculo no se da en la forma estándar. En esta situación, es necesario poner la ecuación en forma estándar y luego determinar el centro y el radio. Para poner la ecuación en forma estándar necesitarás completar el cuadrado. Completar el cuadrado es una técnica matemática que suele ser útil y es la base de cómo se deriva la fórmula cuadrática.

Supongamos que se nos da la ecuación de un círculo que no está en forma estándar:

\[ x^{2}+6 x+y^{2}+10 y+25=0\]

Necesitamos reafirmar esta relación para que el centro y el radio puedan determinarse fácilmente a partir de la ecuación. Para ello, necesitamos completar el cuadrado tanto para las variables como para\(x\) las\(y\) variables. Hay una variedad de métodos para completar el cuadrado voy a demostrar uno de estos a continuación.

Toma la ecuación original y mueve cualquier término que no tenga una variable al otro lado:

\[ x^{2}+6 x+y^{2}+10 y=-25\]

Luego abre un espacio después de la\(6 x\) y la\(10 y:\)

\[ x^{2}+6 x+y^{2}+10 y=-25\]

La idea es que queremos expresiones trinomiales para ambos\(x\) y\(y\) que sean cuadrados perfectos.
Si nos fijamos en la cuadratura de expresiones binomiales, podemos ver que hay un patrón:

\ begin {array} {l}
(x+3) ^ {2} = (x+3) (x+3) =x^ {2} +6 x+9\\
(x+4) ^ {2} =( x+4) (x+4) =x^ {2} +8 x+16\\
(x+5) ^ {2} =( x+5) (x+5) =x^ {2} +10 x+25\\
(x+6) ^ {2} =( x+6) (x+6) =x^ {2} +12 x+36
\ final {matriz}

Podemos ver que si tenemos\(x^{2}+6 x,\) entonces esto correspondería a\((x+3)(x+3)\) o\((x+3)^{2}\). Pero hay un problema: no\((x+3)^{2}\) es igual a\(x^{2}+6 x\). Es igual a No\(x^{2}+6 x+9 .\) podemos simplemente agregar un 9 al\(x^{2}+6 x,\) sino que podemos agregar un 9 a ambos lados.

\[ x^{2}+6 x+9+y^{2}+10 y=-25+9\]

De igual manera, para completar el cuadrado en el\(y,\) vemos que\(y^{2}+10 y\) corresponde a\((x+5)(x+5)\) o\((x+5)^{2}\). Aquí, necesitaríamos agregar 25 a ambos lados para crear un cuadrado perfecto.

\ [\ begin {alineado}
x^ {2} +6 x+9+y^ {2} +10 y+25 &=-25+9+25\\
x^ {2} +6 x+9+y^ {2} +10 y+25 &=9\\
(x+3) ^ {2} + (y+5) ^ {2} &=9
\ end {alineado}
\]

Entonces, el centro del círculo es (-3, -5) y el radio es 3
A veces no es tan obvio cuáles son los valores\(h\) y\(k\) deberían ser en completar el cuadrado. Considera la siguiente ecuación:
\ [x^ {2} +20 x+y^ {2} +30 y+15=0
\] Si miramos hacia atrás a los ejemplos para cuadrar binomios, podemos ver el patrón que relaciona el coeficiente del término lineal con los valores para\(h\) y\(k\)
\ [\ begin {array} {l}
(x+3) ^ {2} =( x+3) (x+3) =x^ {2} +6 x+9\\
(x+4) ^ {2} =( x+4) (x+4) =x^ {2} +8 x+16\\
(x+5) ^ {2} =( x+5) (x+5) =x^ {2} +10 x+25\\
(x+6) ^ {2} =( x+6) (x+6) =x^ {2} +12 x+36
\ end {array}
\] Observe que el coeficiente del término lineal es siempre el doble del valor del numeral entre paréntesis y el término constante es siempre ese número al cuadrado.

\ [(x+n) ^ {2} = (x+n) (x+n) =x^ {2} +2 n x+n^ {2}
\] Entonces, dado el problema anterior,\(x^{2}+20 x+y^{2}+30 y+15=0,\) primero podemos mover el
15 al lado derecho de la ecuación y luego completar los cuadrados en las\(y\) variables\(x\) y.
\ [\ begin {array} {c}
x^ {2} +20 x+y^ {2} +30 y=-15\\
(x+?) ^ {2} + (y+?) ^ {2}\\
x^ {2} +20 x+100+y^ {2} +30 y+225=-15+100+225\\
(x+10) ^ {2} + (y+15) ^ {2} =310
\ end {array}
\] Ahora podemos ver que el centro del círculo está en el punto (-10, -15) y el radio del círculo es\(\sqrt{310} \approx 17.6\)

Ejercicios\(5.1(\mathrm{b})\)

Encuentra el centro y el radio para cada círculo.
Si la ecuación no está escrita en forma estándar, complete el cuadrado para reescribir la ecuación en forma estándar:\((x-h)^{2}+(y-k)^{2}=r^{2}\)

1. \(\quad x^{2}+y^{2}=4\)
2. 2)\(\quad x^{2}+(y-1)^{2}=1\)
3. 3)\(\quad 2(x-3)^{2}+2 y^{2}=8\)
4. 4)\(\quad 3(x+1)^{2}+3(y-1)^{2}=6\)
5. 5)\(\quad x^{2}+y^{2}-2 x-4 y-4=0\)
6. 6)\(\quad x^{2}+y^{2}+4 x+2 y-20=0\)
7. 7)\(\quad x^{2}+y^{2}+4 x-4 y-1=0\)
8. 8)\(\quad x^{2}+y^{2}-6 x+2 y+9=0\)
9. 9)\(\quad 2 x^{2}+2 y^{2}+8 x+7=0\)
10. 10)\(\quad 3 x^{2}+3 y^{2}-12 y=0\)
11. 11)\(\quad 2 x^{2}+2 y^{2}-12 x+8 y-24=0\)
12. 12)\(\quad 2 x^{2}+8 x+2 y^{2}=0\)
13. 13)\(\quad x^{2}+y^{2}+15 x=0\)
14. 14)\(\quad x^{2}+y^{2}+x+y-\frac{1}{2}=0\)
15. 15)\(\quad x^{2}+y^{2}-x+2 y+1=0\)
16. 16)\(\quad 3 x^{2}+3 y^{2}-6 x+3 y=4\)
17. 17)\(\quad 2 x^{2}+2 y^{2}-10 x-18 y=1\)
18. 18)\(\quad 2 x^{2}+2 y^{2}-5 x+y=0\)
19. 19)\(\quad 9 x^{2}+9 y^{2}+9 x-27 y+1=0\)
20. 20)\(\quad 2 x^{2}+2 y^{2}-7 x+y=0\)