5.2: La Ecuación de la Parábola
- Page ID
- 111864
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
La ecuación de la parábola a menudo se da en varias formas diferentes. Una de las formas más simples es:
\ [
(x-h) ^ {2} =4 p (y-k)
\]
Una parábola se define como el locus (o colección) de puntos equidistantes de un punto dado (el foco) y una línea dada (la directrix). Otro punto importante es el vértice o punto de inflexión de la parábola. Si la ecuación de una parábola se da en forma estándar entonces el vértice será\((h, k) .\) El foco será una distancia de\(p\) unidades del vértice dentro de la curva de la parábola y la directrix será una distancia de\(p\) unidades desde el vértice fuera de la curva de la parábola. Este valor\((p)\) se llama distancia focal.
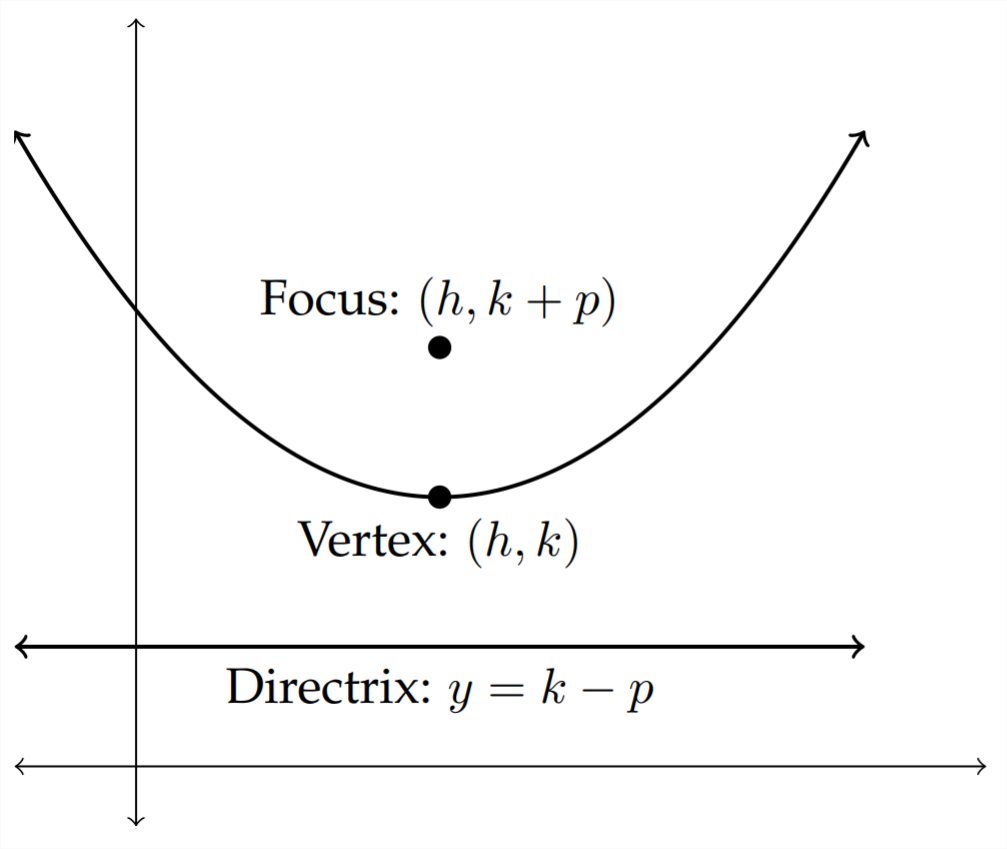
Cualquier punto en la curva de la parábola es equidistante del foco\((h, k+p)\) y la directrix\((h, k-p) .\) Observe que el foco es un punto y se identifica con las coordenadas del punto mientras que la directrix es una línea y se identifica con la ecuación para esa línea.
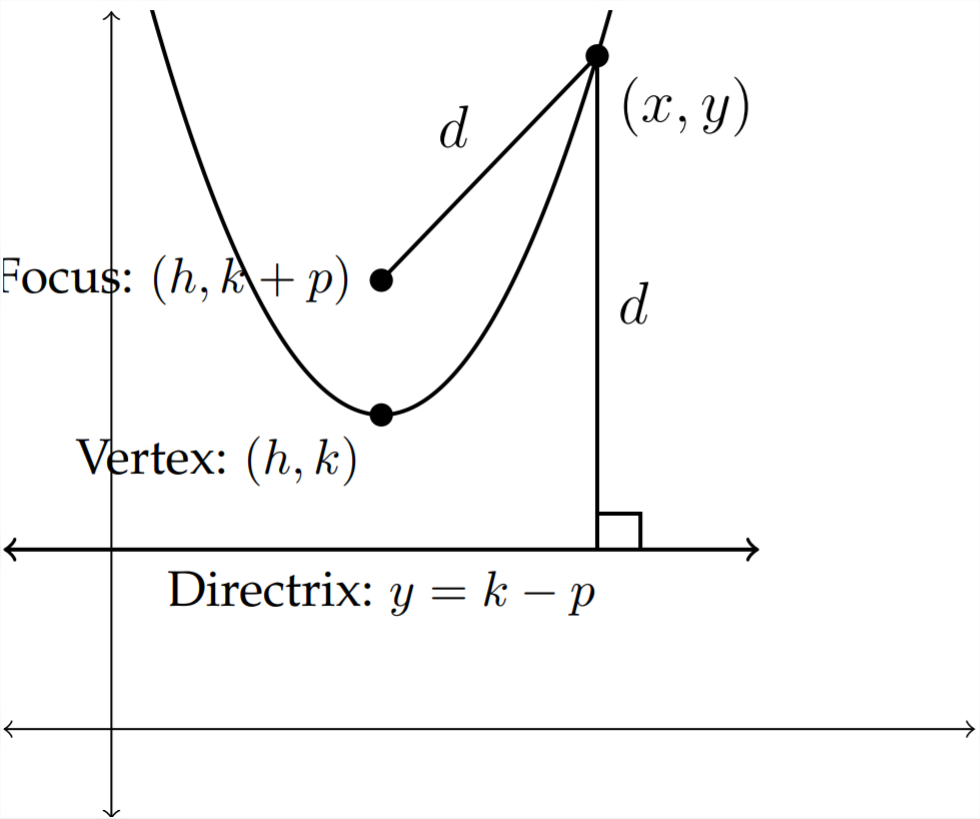
Podemos derivar la ecuación estándar para una parábola usando la fórmula de distancia.
En la imagen de arriba las dos distancias etiquetadas "\(d^{\prime \prime}\)deben ser la misma distancia. La distancia vertical entre el punto\((x, y)\) y la directrix\(y=k-p\) es simplemente la diferencia entre sus\(y\) coordenadas:
\ [
d=y- (k-p)
\]
Para encontrar la distancia entre el punto\((x, y)\) y el foco\((h, k+p)\) nos necesita usar la fórmula de distancia:
\ [
d=\ sqrt {(x-h) ^ {2} + (y- (k+p)) ^ {2}}
\]
Luego establecemos las dos distancias iguales entre sí:
\ [
\ sqrt {(x-h) ^ {2} + (y- (k+p)) ^ {2}} =y- (k-p)
\]
Cuadrar ambos lados :
\ [
(x-h) ^ {2} + (y- (k+p)) ^ {2} =( y- (k-p)) ^ {2}
\]
Tendremos que expandir cada lado y recolectar términos similares, pero dejaremos el\((x-h)^{2}\) solo porque aparecerá de esta forma en la ecuación final.
\ [
(x-h) ^ {2} +y^ {2} -2 (k+p) y+ (k+p) ^ {2} =y^ {2} -2 (k-p) y+ (k-p) ^ {2}
\]
Los\(y^{2}\) términos se cancelan entre sí:
\ [
(x-h) ^ {2} -2 (k+p) y+ (k+p) ^ {2} =-2 (k-p) y+ (k-p) ^ {2}
\]
Ahora vamos a expandir los\(y\) términos\(k, p\) y:
\ [
(x-h) ^ {2} -2 k y-2 p y+k^ {2} +2 p k+p^ {2} =-2 k y+2 p y+k^ {2} -2 p k+p^ {2}
\]
Aquí, los\(p^{2}\) términos\(k^{2}\) y cancelan, al igual que los\(-2 k y\) términos dejando:
\ [
( x-h) ^ {2} -2 p y+2 p k=2 p y-2 p k
\]
Si recogemos todo por encima del\((x-h)^{2}\) lado derecho, tendremos:
\ [
(x-h) ^ {2} =4 p y-4 p k
\]
Factor out\(4 p\) y tenemos la ecuación estándar para a parábola:
\ [
(x-h) ^ {2} =4 p (y-k)
\]
Esta ecuación será diferente dependiendo de la orientación de la parábola. Una parábola orientada hacia arriba tendrá esta ecuación estándar y ambos lados tendrán el mismo signo. Por ejemplo,\((x-5)^{2}=12(y-1)\) es una parábola orientada hacia arriba, como es Se\(-(x-5)^{2}=-12(y-1) .\) puede ver que esta es la misma ecuación, pero se ha multiplicado por -1 en ambos lados.
Una parábola en la que un lado es positivo y un lado negativo, como
\ [
(x+1) ^ {2} =-8 (y-10)
\]
es una parábola orientada hacia abajo. Este formulario también podría aparecer como
\ [
- (x+1) ^ {2} =8 (y-10)
\]
La siguiente imagen ilustra esta situación:

Observe que, en este caso, el foco está por debajo del vértice y la directrix está por encima de él. Recuerda que el foco siempre está en el interior de la curva, mientras que la directrix siempre está fuera de la curva.
Las parábolas también se pueden abrir a la derecha o a la izquierda. En estos casos, es la\(y\) variable que se cuadra en la ecuación estándar:
\ [
(y-k) ^ {2} =4 p (x-h)
\]
En estas situaciones, el foco está a la izquierda o derecha del vértice. Si ambos lados de la ecuación tienen el mismo\(\operatorname{sign},\) tal como\((y-5)^{2}=12(x-1)\) o\(-(y-5)^{2}=-12(x-1)\) entonces esto sería una parábola que se abre a la derecha.

Si los dos lados tienen signos opuestos, entonces la parábola se abrirá hacia la izquierda

La orientación del vértice, foco y directrix nos permite determinar la ecuación de una parábola si se nos dan ciertas piezas de información sobre el vértice, enfoque y directrix. El vértice siempre cae a medio camino entre el foco y la directrix. Los datos clave para determinar la ecuación de una parábola son:
1) el vértice: esto nos da los valores para\(h\) y\(k\) para la ecuación.
2) la orientación: esto nos permite determinar la forma apropiada de la ecuación
a)\(\quad(x-h)^{2}=4 p(y-k)\)
b)\(\quad(x-h)^{2}=-4 p(y-k)\)
c)\(\quad(y-k)^{2}=4 p(x-h)\)
d)\(\quad(y-k)^{2}=-4 p(x-h)\)
Dada la siguiente información determinar un ecuación para la parábola descrita.
Enfocar en (3,2)\(\quad\) Vértice en (1,2)
Primero dibuja un pequeño boceto del problema:

dado que el foco siempre cae dentro del interior de la curva de la parábola, esta parábola está orientada hacia la derecha. Su directrix es la línea\(x=-1\)

La ecuación para esta parábola sería:
\ [
(y-2) ^ {2} =8 (x-1)
\]
Ejercicios\(5.2(a)\)
Determinar la ecuación en forma estándar para cada una de las parábolas que se describen a continuación.
1) Enfoque: (2,5) y vértice: (2,6)
2) Enfoque: (-4,3) y vértice: (-3,3)
3) Enfoque: (1.5,0) y Vetrex: (0,0)
4) Enfoque: (-9,0) y vértice: (-9, -0.5)
5) Enfoque: (5,1) y directrix: x=12
6) Enfoque: (0,3) y directrix: y=1
7) Enfoque: (1, -3) y Directrix: y=2
8) Foco: (-4,8) y Directrix: x=-6
9) Vértice: (1,3), eje de simetría paralelo a\(y\) -eje
contiene el punto (4,7.5)
10) Vértice: (4,2), eje de simetría paralelo a\(y\) -eje
contiene el punto (5,0)
11) Enfoque: (0,0) y vértice: (0, -1.25)
12) Enfoque: (0,0) y vértice: (0,2.5)
13) Enfoque: (2,7) y Directrix: x=0.5
14) Enfoque: (-3,0) y Directrix: x=-2
15) Vértice: (3, -2), eje de simetría paralela a\(x\) -eje,
contiene el punto (7,3)
16) Vértice: (-6, -6), eje de simetría paralelo a\(y\) -eje,
contiene el punto (0,0)
Si se nos da la ecuación de una parábola y necesitamos encontrar el vértice, el foco y la directrix, a menudo es útil poner la ecuación en forma estándar. Esto suele requerir completar la plaza.
Si nos dan la ecuación:
\ [
x^ {2} +6 x-4 y+1 = 0
\]
entonces sabemos que esta será una parábola orientada hacia arriba o hacia abajo. Alejemos todo de los\(x\) términos pero dejemos un espacio para completar el
cuadrado:
\ [
x^ {2} +6 x=4 y-1
\]
Para completar el cuadrado en este, necesitamos agregar 9 a ambos lados para que podamos reescribir el lado izquierdo como\((x+3)^{2}\)
\ [
\ begin {aligned}
x^ {2} +6 x+9 &=4 y-1+9\\
(x+3) ^ {2} &=4 y+8
\ end {alineado}
\]
Entonces podemos factorizar el coeficiente de la\(y\) variable (incluso si no factoriza uniformemente).
\ [
(x+3) ^ {2} =4 (y+2)
\]
Entonces, esta es una parábola orientada hacia arriba con el vértice en el punto (-3, -2). Para encontrar el foco y directrix, necesitamos conocer la vlaue de\(p .\) desde\(4 p=4,\) entonces sabemos que\(p=1 .\) Esto quiere decir que el foco estará 1 unidad por encima del vértice en el punto (-3, -1) y la directrix será una unidad por debajo del vértice en la línea y=-3.
\ begin {array} {c}
\ text {Vertex:}\ quad (-3, -2)\\
\ text {Enfoque:}\ quad (-3, -1)\\
\ text {Directrix:}\ quad (y=-3)
\ end {array}
Aquí hay otro ejemplo:
Exprese el en forma estándar y determinar el vértice, foco y directrix de la siguiente parábola.
\ [
y^ {2} -2 y-1+8 x=0
\]
Sabemos que esta parábola estará orientada a la derecha o a la izquierda.
Primero, movamos todos los términos que no contengan\(y\) hacia el lado derecho sino dejemos espacio para completar el cuadrado.
\ [
y^ {2} -2 y=-8 x+1
\]
Agrega 1 a ambos lados para completar el cuadrado:
\ [
\ begin {aligned}
y^ {2} -2 y+1 &=-8 x+1+1\\
(y-1) ^ {2} &=-8 x+2
\ end {alineado}
\]
Factorizar el coeficiente de la\(x\) variable:
\ [
(y-1) ^ {2} =-8 (x-0.25)
\]
Entonces, esta es una parábola orientada a la izquierda con un vértice en el punto\((0.25,1) .\) Para encontrar la distancia focal, decimos que\(4 p=-8,\) así\(p=-2\)
ya que está orientado a la izquierda, el foco será una distancia de 2 unidades a la izquierda del vértice en el punto (-1.75,1) y la directrix será una distancia de 2 unidades a la derecha del vértice en la línea\(x=2.25\)
Ejercicios\(5.2(b)\)
Expresa cada ecuación en forma estándar y determina el vértice, enfoque y directrix de cada parábola.
Forma estándar:
\ [
\ begin {array} {l}
4 p (y-k) =( x-h) ^ {2}\\
4 p (x-h) =( y-k) ^ {2}
\ end {array}
\]
1)\(\quad (x-2)^{2}=8(y+1)\)
2)\(\quad (x+5)^{2}=12(y-3)\)
3)\(\quad (y+1)^{2}=6(x-2)\)
4) \(\quad (y+4)^{2}=10(x+1)\)
5)\(\quad (x+3)^{2}=-5(y+2)\)
6)\(\quad (x-4)^{2}=-7(y-6)\)
7)\(\quad (y+8)^{2}=-6(x+4)\)
8)\(\quad (y-3)^{2}=-9(x+4)\)
9)\(\quad (x^{2}+8 x+y+6=0\)
10)\(\quad x^{2}+6 x+y-3=0\)
11)\(\quad y^{2}+6 y+8 x+1=0\)
12)\(\quad y^{2}+8 y-4 x+8=0\)
13)\(\quad x^{2}+4 x-3 y+7=0\)
14)\(\quad x^{2}+2 x-6 y-11=0\)
15)\(\quad y^{2}+6 y-4 x+4=0\)
16)\(\quad y^{2}-4 y+3 x+9=0\)
17)\(\quad x+y^{2}-3 y+1=0\)
18)\(\quad 10+x+y^{2}+5 y=0\)
19)\(\quad x+y^{2}-3 y+4=0\)
20)\(\quad 3 x+y^{2}+8 y+4=0\)
21)\(\quad x^{2}+3 x+3 y-1=0\)
22)\(\quad x^{2}+5 x-4 y-1=0\)
23)\(\quad x^{2}-8 x-4 y+3=0\)
24)\(\quad 6 x-y^{2}-12 y+4=0\)
25)\(\quad 2 x+4 y^{2}+8 y-5=0\)
26)\(\quad 4 x^{2}-12 x+12 y+7=0\)
27)\(\quad 3 x^{2}-6 x-9 y+4=0\)
28)\(\quad 2 x-3 y^{2}+9 y+5=0\)
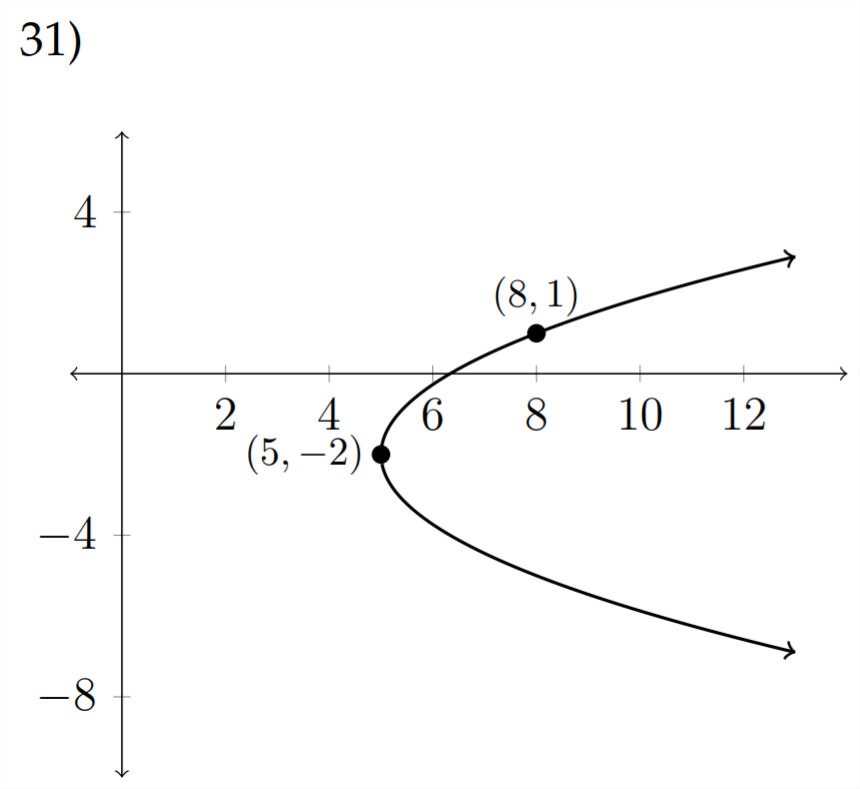
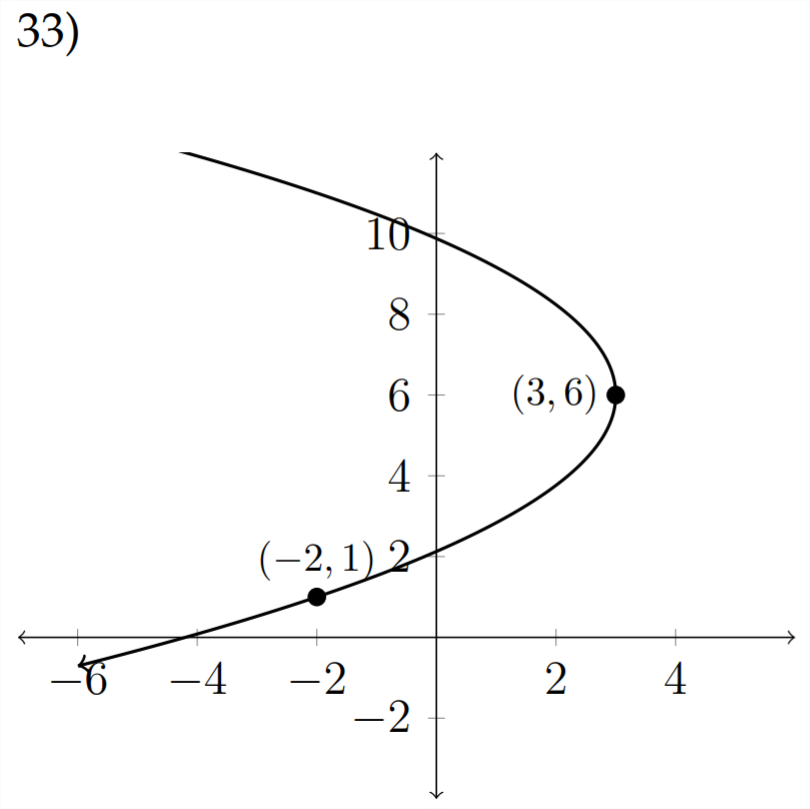
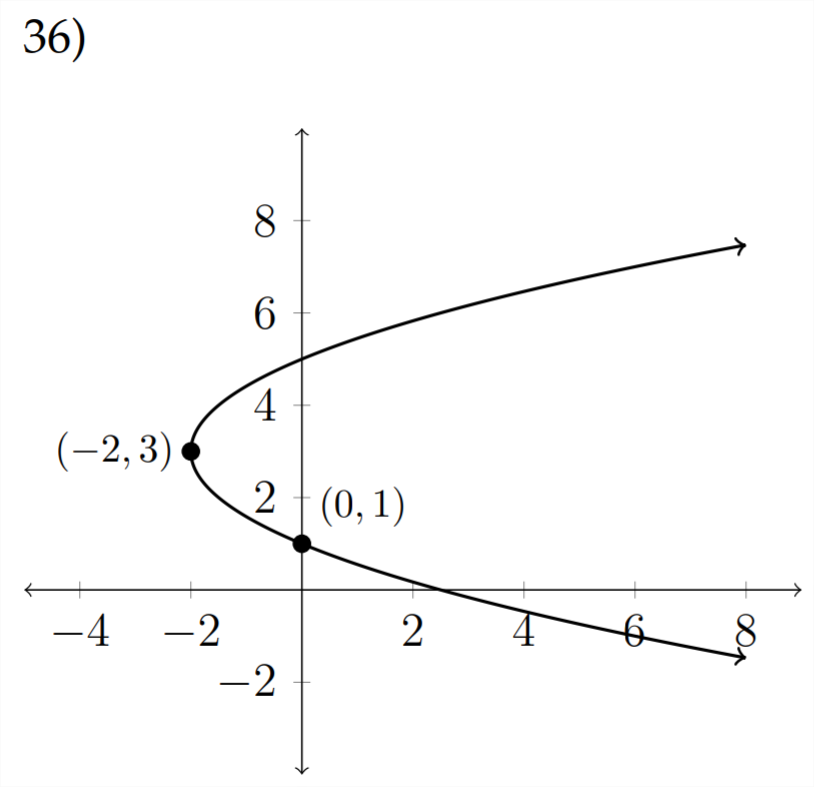
Escribe una ecuación en forma estándar para cada parábola que se muestra a continuación.