7.1: El principio fundamental del conteo

Última actualización
Guardar como PDF

Page ID: 111939

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La combinatoria es un área importante de lo que generalmente se conoce como “Matemáticas Discretas”. La palabra discreto se refiere a cantidades que son individuales, separadas o distintas. Esto crea una división importante en matemáticas entre “matemáticas continuas” y “matemáticas discretas”. La diferencia entre estas dos áreas es que las matemáticas continuas consideran y utilizan todas las partes de la recta numérica números enteros, números racionales (fracciones), números irracionales y así sucesivamente. Las matemáticas discretas suelen utilizar solo los números enteros.

En lugar de limitar las posibilidades en matemáticas, esta restricción en realidad abre nuevas y sorprendentes áreas de consideración. Los códigos binarios que utilizan las computadoras generalmente se controlan y se mantienen (en su mayoría) libres de errores mediante el uso de matemáticas discretas. La seguridad informática para la información digital más simple (comprobando su saldo bancario en línea) y la más compleja (datos clasificados de alto nivel) se maneja a través de un cifrado que se basa en los conceptos de matemáticas discretas.

Cualquier tipo de aplicación en las ciencias que implique elecciones y posibilidades suele utilizar los conceptos de combinatoria. La química combinatoria explora los resultados cuando se agregan una serie de diferentes grupos químicos a la misma estructura química básica para investigar las cualidades del compuesto resultante. Además, la combinatoria es muy importante para el estudio de la probabilidad. Para calcular la probabilidad de un evento, a menudo es necesario calcular cuántos

diferentes maneras en que algo puede suceder.
La primera idea importante de la combinatoria es el principio fundamental del conteo. Esta es la idea de que si dos eventos ocurren en sucesión y hay$m$ formas de hacer el primero y$n$ formas de hacer el segundo (después de que haya ocurrido el primero), entonces hay$m * n$ formas de completar las dos tareas en sucesión.

Por ejemplo, al lanzar dos dados de seis caras, hay 36 posibilidades: seis posibilidades desde el primer dado y seis desde el segundo. Estas posibilidades se enumeran a continuación:
$clipboard_e186c4a32a665b07b79f1269ff2426ae7.png$
Si tuviéramos que lanzar un dado de seis lados y un dado de ocho lados, entonces habría$6 * 8=48$ diferentes posibilidades.

Muchas veces la creación de un diagrama de árbol puede ayudarnos a visualizar las posibilidades. Supongamos que se crea un código de tres dígitos usando los números 0,1 y 2 para que se permita la repetición de los números. Habría 3 posibilidades para el primer número, tres para el segundo número y tres para el tercer número, lo que significa que habría un total de$3 * 3 * 3=27$ diferentes códigos posibles.
El diagrama de árbol para ilustrar esto se muestra en la página siguiente.
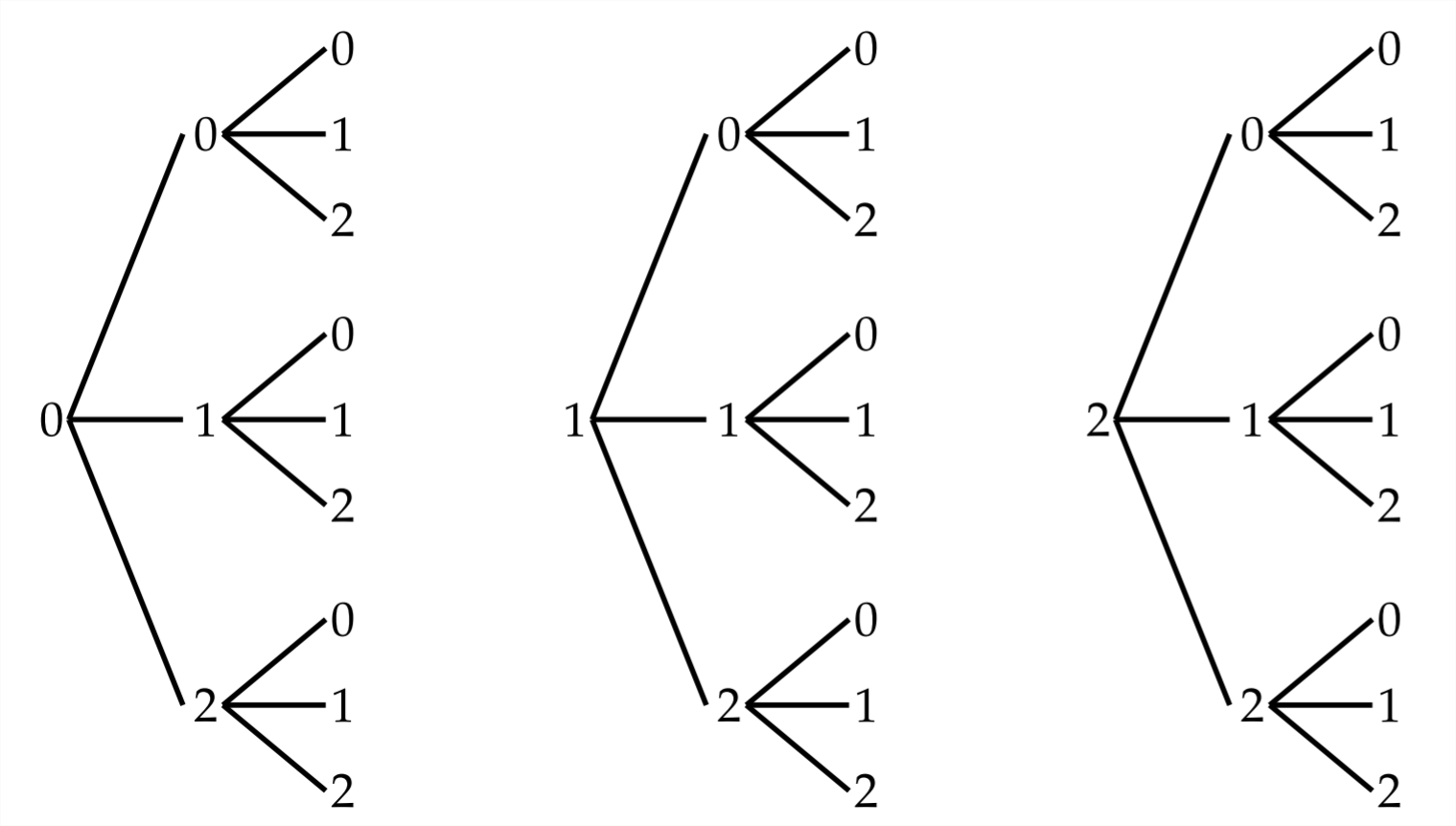
$clipboard_ec71ce7e5d3909ab5b777c86a60e13345.png$

Todas las posibilidades están listadas y se pueden construir a partir del diagrama de árbol.
Aquí hay algunos problemas de muestra para usar el principio fundamental del conteo (también conocido como el principio de multiplicación).

Ejemplo:
Una heladería ofrece helados de Vainilla, Chocolate, Fresa, Boysenberry y Rocky Road. El helado viene con un cono de gofre, un cono de azúcar o un cono de oblea y puede ser simple o con chispas. ¿Cuántas formas diferentes hay de pedir una sola cucharada de helado?

Con 5 tipos diferentes de helado, 3 conos diferentes y 2 opciones para chispas, habría$5 * 3 * 2=30$ diferentes posibilidades.

Ejemplo:
En muchos estados las placas para automóviles constan de tres letras seguidas de tres números.
¿Cuántas posibilidades diferentes hay:
si se permite la repetición de letras y números?
si no se permite la repetición de letras y números?
Hay seis posiciones para letras y números que conforman la matrícula.
Los tres primeros deben ser letras y los segundos tres números.
Hay 26 opciones para las tres primeras y 10 opciones para las segundas tres, por lo que hay$26 * 26 * 26 * 10 * 10 * 10=17,576,000$ posibles matrículas si se permite la repetición.

Si no se permite la repetición, entonces tenemos que descontar la letra o número que se elija para un puesto en particular. Entonces, para la primera letra hay 26 posibilidades, pero luego sólo 25 para la segunda letra y 24 para la tercera. De igual manera, con los números hay 10 opciones inicialmente, luego 9 opciones y luego 8
Entonces, la solución sin repetición sería$26 * 25 * 24 * 10 * 9 * 8=11,232,000$

4)$\quad$ Una moneda es volteada cinco veces y se registra el resultado cada vez. ¿Cuántos resultados diferentes hay?
5)$\quad$ Se voltea una moneda y se enrolla una matriz de seis caras y se registran los resultados. Si esto se hace tres veces, ¿cuántos resultados posibles hay?
6)$\quad$ Se eligen dos cartas de una baraja de 52 cartas. Si la primera carta no es reemplazada antes de elegir la segunda carta, ¿cuántas formas hay de elegir: a)
$\quad$ Una pala primero y un segundo corazón?
b) ¿$\quad$Dos espadas?
7)$\quad$ Una empresa cuenta con 3000 empleados. Planean implementar un sistema de numeración de identificación de empleado que consistiría en una letra seguida de dos dígitos. ¿Es posible darle a cada empleado un código de identificación diferente bajo este plan?
8)$\quad$ Un equipo de beisbol cuenta con 7 lanzadores y 3 captadores. ¿Cuántas baterías diferentes (combinaciones de lanzador - receptor) son posibles?
9)$\quad$ Se crea una cadena de cinco letras usando las letras$\mathrm{A}, \mathrm{B}, \mathrm{C}, \mathrm{D}$ y E. Cuantas de estas cadenas de letras son posibles si:
$\quad$ a)$\quad$ No se imponen condiciones
$\quad$ b) No$A$ se permite la repetición de la letra
$\quad$c) Cada cadena de letras debe comenzar con$C$
$\quad$ d)$\quad$ B debe ser la letra media
$\quad$ e)$\quad$$A, B$ y$C$ deben ser las letras medias en cualquier orden sin repetición
Para Parte ( e) por favor enumere todas las posibilidades.
10) (\ quad\) Un candado de combinación está numerado del 0 al 30. Cada combinación consta de tres números en sucesión. Los números sucesivos deben ser diferentes, pero el primero y el tercero pueden ser iguales. ¿Cuántas combinaciones diferentes son posibles?