2.4: Números Complejos

Última actualización
Guardar como PDF

Page ID: 111976

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Sumar y restar números complejos.
Multiplicar y dividir números complejos.
Resolver ecuaciones cuadráticas con números complejos

Descubierto por Benoit Mandelbrot alrededor de 1980, el Set Mandelbrot es una de las imágenes fractales más reconocibles. La imagen se construye sobre la teoría de la auto-similitud y la operación de iteración. Hacer zoom sobre una imagen fractal trae muchas sorpresas, particularmente en el alto nivel de repetición de detalles que aparece a medida que aumenta la ampliación. La ecuación que genera esta imagen resulta ser bastante simple.

Una representación visual del conjunto de Mandelbrot — Figura$\PageIndex{1}$: El conjunto de Mandelbrot exhibe similitud, la cual se muestra mejor en una animación.

Para entenderlo mejor, necesitamos familiarizarnos con un nuevo conjunto de números. Hay que tener en cuenta que el estudio de las matemáticas se construye continuamente sobre sí mismo. Los enteros negativos, por ejemplo, llenan un vacío dejado por el conjunto de enteros positivos. El conjunto de números racionales, a su vez, llena un vacío dejado por el conjunto de enteros. El conjunto de números reales llena un vacío dejado por el conjunto de números racionales. No es sorprendente que el conjunto de números reales también tenga vacíos. En esta sección, exploraremos un conjunto de números que llena vacíos en el conjunto de números reales y descubriremos cómo trabajar dentro de él.

Expresando raíces cuadradas de números negativos como múltiplos de$i$

Sabemos encontrar la raíz cuadrada de cualquier número real positivo. De manera similar, podemos encontrar la raíz cuadrada de cualquier número negativo. La diferencia es que la raíz no es real. Si el valor en el radicando es negativo, se dice que la raíz es un número imaginario.El número imaginario$i$ se define como la raíz cuadrada de$−1$.

\[\sqrt{-1}=i\]

Entonces, usando las propiedades de los radicales,

\[i^2=(\sqrt{-1})^2=-1\]

Podemos escribir la raíz cuadrada de cualquier número negativo como múltiplo de$i$. Considera la raíz cuadrada de$−49$.

\[\begin{align*} \sqrt{-49}&= \sqrt{49\times(-1)}\\[4pt] &= \sqrt{49}\sqrt{-1}\\[4pt] &= 7i \end{align*}\]

Usamos$7i$ y no$−7i$ porque la raíz principal de$49$ sea la raíz positiva.

Un número complejo es la suma de un número real y un número imaginario. Un número complejo se expresa en forma estándar cuando se escribe$a+bi$ donde$a$ está la parte real y$b$ es la parte imaginaria. Por ejemplo,$5+2i$ es un número complejo. Entonces, también, lo es$3+4i\sqrt{3}$.

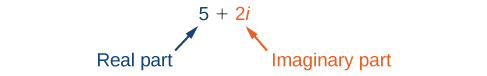
$Se muestra el número complejo 5 + 2i. El 5 está etiquetado como: Parte real y el 2i está etiquetado como: Parte imaginaria$

Los números imaginarios difieren de los números reales en que un número imaginario cuadrado produce un número real negativo. Recordemos que cuando se cuadra un número real positivo, el resultado es un número real positivo y cuando se cuadra un número real negativo, el resultado también es un número real positivo. Los números complejos consisten en números reales e imaginarios.

Definición: Números imaginarios y complejos

Un número complejo es un número de la forma$a+bi$ donde

$a$es la parte real del número complejo.
$b$es la parte imaginaria del número complejo.

Si$b=0$, entonces$a+bi$ es un número real. Si$a=0$ y no$b$ es igual a$0$, el número complejo se llama un número imaginario puro. Un número imaginario es una raíz par de un número negativo.

Cómo: Dado un número imaginario, expresarlo en la forma estándar de un número complejo

Escribir$\sqrt{-a}$ como$\sqrt{a}\sqrt{-1}$.
Expresar$\sqrt{-1}$ como$i$.
Escribe$\sqrt{a}\times i$ en la forma más simple.

Ejemplo$\PageIndex{1}$: Expressing an Imaginary Number in Standard Form

Express$\sqrt{-9}$ en forma estándar.

Solución

\[\begin{align*} \sqrt{-9}&= \sqrt{9}\sqrt{-1)}\\[4pt] &= 3i\\[4pt] \end{align*}\]

En forma estándar, esto es$0+3i$.

Ejercicio$\PageIndex{1}$

Express$\sqrt{-24}$ en forma estándar.

Contestar: $\sqrt{-24}=0+2i\sqrt{6}$

Trazar un número complejo en el plano complejo

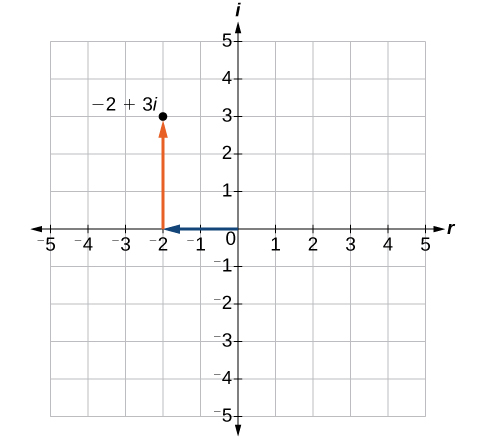
No podemos trazar números complejos en una recta numérica, ya que podríamos números reales. Sin embargo, todavía podemos representarlos gráficamente. Para representar un número complejo, necesitamos abordar los dos componentes del número. Utilizamos el plano complejo, que es un sistema de coordenadas en el que el eje horizontal representa el componente real y el eje vertical representa el componente imaginario. Los números complejos son los puntos en el plano, expresados como pares ordenados$(a,b)$, donde$a$ representa la coordenada para el eje horizontal y$b$ representa la coordenada para el eje vertical.

Consideremos el número$−2+3i$. La parte real del número complejo es$−2$ y la parte imaginaria es$3$. Trazamos el par ordenado$(−2,3)$ para representar el número complejo$−2+3i$, como se muestra en la Figura$\PageIndex{2}$.

Plano de coordenadas con los ejes x e y que van de 5 a 5 negativos. El punto negativo 2 más 3i se traza en la gráfica. Una flecha se extiende hacia la izquierda desde el origen dos unidades y luego una flecha se extiende hacia arriba tres unidades desde el final de la flecha anterior. — Figura$\PageIndex{2}$

PLANO COMPLEJO

En el plano complejo, el eje horizontal es el eje real, y el eje vertical es el eje imaginario, como se muestra en la Figura$\PageIndex{3}$.

Un plano de coordenadas en blanco con el eje x etiquetado: real y el eje y etiquetado: imaginario. — Figura$\PageIndex{3}$

Cómo: Dado un número complejo, representar sus componentes en el plano complejo

Determinar la parte real y la parte imaginaria del número complejo.
Muévase a lo largo del eje horizontal para mostrar la parte real del número.
Muévase paralelo al eje vertical para mostrar la parte imaginaria del número.
Trazar el punto.

Ejemplo$\PageIndex{2}$: Plotting a Complex Number on the Complex Plane

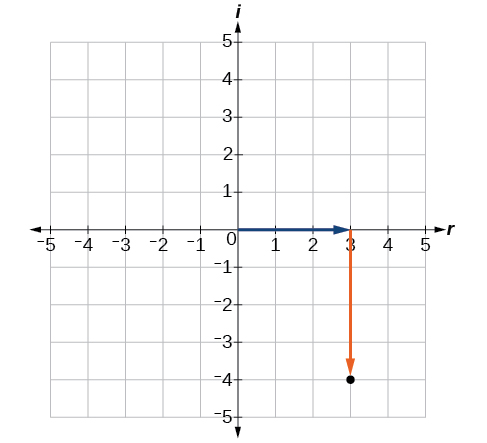
Trazar el número complejo$3−4i$ en el plano complejo.

Solución

La parte real del número complejo es$3$, y la parte imaginaria lo es$–4$. Trazamos el par ordenado$(3,−4)$ como se muestra en la Figura$\PageIndex{4}$.

Plano de coordenadas con los ejes x e y que van de -5 a 5. Se traza el punto 3 — 4i, con una flecha que se extiende hacia la derecha desde el origen 3 unidades y una flecha que se extiende hacia abajo 4 unidades desde el final de la flecha anterior. — Figura$\PageIndex{4}$

Ejercicio$\PageIndex{2}$

Trazar el número complejo$−4−i$ en el plano complejo.

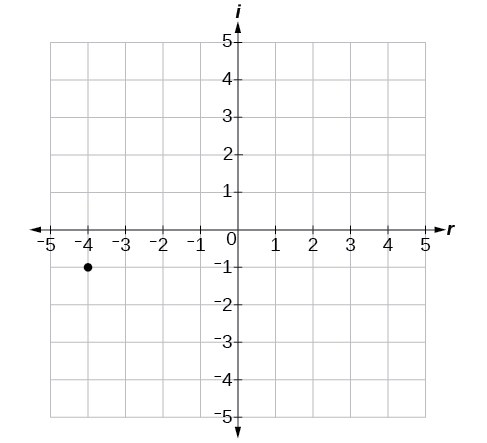
Contestar: $Plano de coordenadas con los ejes x e y que van de 5 a 5 negativos. Se traza el punto -4 i.$
Figura$\PageIndex{5}$

Sumando y restando números complejos

Al igual que con los números reales, podemos realizar operaciones aritméticas en números complejos. Para sumar o restar números complejos, combinamos las partes reales y luego combinamos las partes imaginarias.

Números complejos: suma y resta

Sumando números complejos:

\[(a+bi)+(c+di)=(a+c)+(b+d)i\]

Restar números complejos:

\[(a+bi)−(c+di)=(a−c)+(b−d)i\]

Cómo: Dados dos números complejos, encuentra la suma o diferencia

Identificar las partes reales e imaginarias de cada número.
Sumar o restar las partes reales.
Suma o resta las partes imaginarias.

Ejemplo$\PageIndex{3}$: Adding and Subtracting Complex Numbers

Sumar o restar como se indica.

$(3−4i)+(2+5i)$
$(−5+7i)−(−11+2i)$

Solución

\[\begin{align*} (3-4i)+(2+5i)&= 3-4i+2+5i\\[4pt] &= 3+2+(-4i)+5i\\[4pt] &= (3+2)+(-4+5)i\\[4pt] &= 5+i \end{align*}\]
\[\begin{align*} (-5+7i)-(-11+2i)&= -5+7i+11-2i\\[4pt] &= -5+11+7i-2i\\[4pt] &= (-5+11)+(7-2)i\\[4pt] &= 6+5i \end{align*}\]

Ejercicio$\PageIndex{3}$

Restar$2+5i$ de$3–4i$.

Contestar: $(3−4i)−(2+5i)=1−9i$

Multiplicar números complejos

Multiplicar números complejos es muy parecido a multiplicar binomios. La mayor diferencia es que trabajamos con las partes real e imaginaria por separado.

Multiplicar un número complejo por un número real

Comencemos multiplicando un número complejo por un número real. Distribuimos el número real tal como lo haríamos con un binomio. Considere, por ejemplo,$3(6+2i)$:

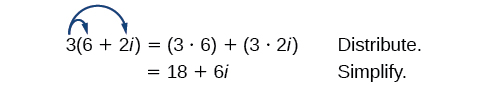
$Multiplicación de un número real y un número complejo. El 3 fuera de los paréntesis tiene flechas que se extienden desde él tanto al 6 como al 2i dentro de los paréntesis. Esta expresión se establece igual a la cantidad tres por seis más la cantidad tres por dos veces i; esta es la propiedad distributiva. La siguiente línea equivale a dieciocho más seis veces i; la simplificación.$

Cómo: Dado un número complejo y un número real, multiplique para encontrar el producto

Utilice la propiedad distributiva.
Simplificar.

Ejemplo$\PageIndex{4}$: Multiplying a Complex Number by a Real Number

Encuentra el producto$4(2+5i)$.

Solución

Distribuir el$4$.

\[\begin{align*} 4(2+5i)&= (4\cdot 2)+(4\cdot 5i)\\[4pt] &= 8+20i \end{align*}\]

Ejercicio$\PageIndex{4}$

Encuentra el producto:$\dfrac{1}{2}(5−2i)$.

Contestar: $\dfrac{5}{2}-i$

Multiplicar números complejos juntos

Ahora, multipliquemos dos números complejos. Podemos usar ya sea la propiedad distributiva o más específicamente el método FOIL porque estamos tratando con binomios. Recordemos que FOIL es un acrónimo para multiplicar los términos Primero, Interior, Exterior y Último juntos. La diferencia con los números complejos es que cuando obtenemos un término cuadrado,$i^2$, es igual$-1$.

\[\begin{align*} (a+bi)(c+di)&= ac+adi+bci+bdi^2\\[4pt] &= ac+adi+bci-bd(-1)\qquad i^2 = -1\\[4pt] &= ac+adi+bci-bd\\[4pt] &= (ac-bd)+(ad+bc)i \end{align*}\]

Agrupar términos reales y términos imaginarios.

Cómo: Dados dos números complejos, multiplique para encontrar el producto

Utilice la propiedad distributiva o el método FOIL.
Recuerda eso$i^2=-1$.
Agrupar los términos reales y los términos imaginarios

Ejemplo$\PageIndex{5}$: Multiplying a Complex Number by a Complex Number

Multiplicar$(4+3i)(2−5i)$.

Solución

\[\begin{align*} (4+3i)(2-5i)&= 4(2)-4(5i)+3i(2)-(3i)(5i)\\[4pt] &= 8-20i+6i-15(i^2)\\[4pt] &= (8+15)+(-20+6)i\\[4pt] &= 23-14i \end{align*}\]

Ejercicio$\PageIndex{5}$

Multiplicar:$(3−4i)(2+3i)$.

Contestar: $18+i$

Dividir números complejos

Dividir dos números complejos es más complicado que sumar, restar o multiplicar porque no podemos dividir por un número imaginario, lo que significa que cualquier fracción debe tener un denominador de número real para escribir la respuesta en forma estándar$a+bi$. Necesitamos encontrar un término por el que podamos multiplicar el numerador y el denominador que elimine la porción imaginaria del denominador para que terminemos con un número real como denominador. A este término se le llama el conjugado complejo del denominador, que se encuentra cambiando el signo de la parte imaginaria del número complejo. En otras palabras, el complejo conjugado de$a+bi$ es$a−bi$. Por ejemplo, el producto de$a+bi$ y$a−bi$ es

\[\begin{align*} (a+bi)(a-bi)&= a^2-abi+abi-b^2i^2\\[4pt] &= a^2+b^2 \end{align*}\]

El resultado es un número real.

Tenga en cuenta que los conjugados complejos tienen una relación opuesta: El conjugado complejo de$a+bi$ es$a−bi$, y el conjugado complejo de$a−bi$ es$a+bi$. Además, cuando una ecuación cuadrática con coeficientes reales tiene soluciones complejas, las soluciones son siempre conjugados complejos entre sí.

Supongamos que queremos dividir$c+di$ por$a+bi$, donde$a$ ni ni$b$ es igual a cero. Primero escribimos la división como una fracción, luego encontramos el complejo conjugado del denominador, y multiplicamos.

$\dfrac{c+di}{a+bi}$dónde$a≠0$ y$b≠0$

Multiplique el numerador y el denominador por el complejo conjugado del denominador.

\[\begin{align*} \dfrac{(c+di)}{(a+bi)}\cdot \dfrac{(a-bi)}{(a-bi)}&= \dfrac{(c+di)(a-bi)}{(a+bi)(a-bi)}\\[4pt] &= \dfrac{ca-cbi+adi-bdi^2}{a^2-abi+abi-b^2i^2} \qquad \text{Apply the distributive property}\\[4pt] &= \dfrac{ca-cbi+adi-bd(-1)}{a^2-abi+abi-b^2(-1)} \qquad \text{Simplify, remembering that } i^2=-1\\[4pt] &= \dfrac{(ca+bd)+(ad-cb)i}{a^2+b^2} \end{align*}\]

Definición: EL CONEJADO COMPLEJO

El conjugado complejo de un número complejo$a+bi$ es$a−bi$. Se encuentra cambiando el signo de la parte imaginaria del número complejo. La parte real del número se deja sin cambios.

Cuando un número complejo se multiplica por su conjugado complejo, el resultado es un número real.
Cuando se agrega un número complejo a su conjugado complejo, el resultado es un número real.

Ejemplo$\PageIndex{6}$: Finding Complex Conjugates

Encuentra el complejo conjugado de cada número.

$2+i\sqrt{5}$
$-\dfrac{1}{2}i$

Solución

El número ya está en la forma$a+bi$. El conjugado complejo es$a−bi$, o$2−i\sqrt{5}$.
Podemos reescribir este número en la forma$a+bi$ como$0−\dfrac{1}{2}i$. El conjugado complejo es$a−bi$, o$0+\dfrac{1}{2}i$. Esto se puede escribir simplemente como$\dfrac{1}{2}i$.

Análisis

Si bien hemos visto que podemos encontrar el complejo conjugado de un número imaginario, en la práctica generalmente encontramos los conjugados complejos de solo números complejos con un componente tanto real como imaginario. Para obtener un número real a partir de un número imaginario, simplemente podemos multiplicar por$i$.

Ejercicio$\PageIndex{6}$

Encuentra el complejo conjugado de$−3+4i$.

Contestar: $−3−4i$

Cómo: Dados dos números complejos, dividir uno por otro

Escribe el problema de división como una fracción.
Determinar el complejo conjugado del denominador.
Multiplique el numerador y denominador de la fracción por el complejo conjugado del denominador.
Simplificar.

Ejemplo$\PageIndex{7}$: Dividing Complex Numbers

Dividir$(2+5i)$ por$(4−i)$.

Solución

Comenzamos por escribir el problema como una fracción.

\[\dfrac{(2+5i)}{(4−i)} \nonumber \]

Después multiplicamos el numerador y el denominador por el complejo conjugado del denominador.

\[\dfrac{(2+5i)}{(4−i)}⋅\dfrac{(4+i)}{(4+i)} \nonumber \]

Para multiplicar dos números complejos, ampliamos el producto como lo haríamos con polinomios (usando FOIL).

\[\begin{align*} \dfrac{(2+5i)}{(4-i)}\cdot \dfrac{(4+i)}{(4+i)}&= \dfrac{8+2i+20i+5i^2}{16+4i-4i-i^2}\\[4pt] &= \dfrac{8+2i+20i+5(-1)}{16+4i-4i-(-1)}\; i^2=-1 \\[4pt] &= \dfrac{3+22i}{17}\\[4pt] &= \dfrac{3}{17}+\dfrac{22}{17i} \end{align*}\]

Separar partes reales e imaginarias.

Tenga en cuenta que esto expresa el cociente en forma estándar.

Simplificación de los poderes de$i$

Los poderes de$i$ son cíclicos. Veamos qué pasa cuando elevamos$i$ a poderes crecientes.

\[i^1=i \nonumber \]\[i^2=-1 \nonumber \]\[i^3=i^2⋅i=-1⋅i=-i \nonumber \]\[i^4=i^3⋅i=-i⋅i=-i^2=-(-1)=1 \nonumber \]\[i^5=i^4⋅i=1⋅i=i \nonumber \]

Podemos ver que cuando llegamos al quinto poder de i, es igual al primer poder. A medida que sigamos multiplicándonos$i$ por el aumento de poderes, veremos un ciclo de cuatro. Examinemos los siguientes cuatro poderes de$i$.

\[i^6=i^5⋅i=i⋅i=i^2=-1 \nonumber \]\[i^7=i^6⋅i=i^2⋅i=i^3=-i \nonumber \]\[i^8=i^7⋅i=i^3⋅i=i^4=1 \nonumber \]\[i^9=i^8⋅i=i^4⋅i=i^5=i \nonumber \]

El ciclo se repite continuamente:$i,−1,−i,1,$ cada cuatro potencias.

Ejemplo$\PageIndex{8}$: Simplifying Powers of $i$

Evaluar:$i^{35}$.

Solución

Ya que$i^4=1$, podemos simplificar el problema factorizando tantos factores$i^4$ como sea posible. Para ello, primero determine cuántas veces$4$ entra en$35: 35=4⋅8+3$.

\[i^{35}=i^{4⋅8+3}=i^{4⋅8}⋅i^3={(i^4)}^8⋅i^3=i^8⋅i^3=i^3=−i \nonumber \]

Ejercicio$\PageIndex{7}$

Evaluar:$i^{18}$

Contestar: $−1$

Q&A

¿Podemos escribir$i^{35}$ de otras maneras útiles?

Como vimos en Ejemplo$\PageIndex{8}$, reducimos$i^{35}$ a$i^3$ dividiendo el exponente por$4$ y usando el resto para encontrar la forma simplificada. Pero quizás otra factorización de$i^{35}$ puede ser más útil. $\PageIndex{1}$El cuadro muestra algunas otras factorizaciones posibles.

Mesa$\PageIndex{1}$
Factorización de$i^{35}$	$i^{34}⋅i$	$i^{33}⋅i^2$	$i^{31}⋅i^4$	$i^{19}⋅i^{16}$
Forma reducida	${(i^2)}^{17}⋅i$	$i^{33}⋅(−1)$	$i^{31}⋅1$	$i^{19}⋅{(i^4)}^4$
Forma simplificada	${(−1)}^{17}⋅i$	$−i^{33}$	$i^{31}$	$i^{19}$

Cada uno de estos eventualmente dará como resultado la respuesta que obtuvimos anteriormente, pero puede requerir varios pasos más que nuestro método anterior.

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con números complejos.

Sumando y restando números complejos
Multiplicar números complejos
Multiplicar conjugados complejos
Elevar i a Poderes

Conceptos clave

La raíz cuadrada de cualquier número negativo se puede escribir como un múltiplo de $i$. Ver Ejemplo.
Para trazar un número complejo, utilizamos dos líneas numéricas, cruzadas para formar el plano complejo. El eje horizontal es el eje real, y el eje vertical es el eje imaginario. Ver Ejemplo.
Los números complejos se pueden sumar y restar combinando las partes reales y combinando las partes imaginarias. Ver Ejemplo.
Los números complejos se pueden multiplicar y dividir.
- Para multiplicar números complejos, distribuir igual que con polinomios. Ver Ejemplo y Ejemplo.
- Para dividir números complejos, multiplique tanto el numerador como el denominador por el conjugado complejo del denominador para eliminar el número complejo del denominador. Ver Ejemplo y Ejemplo.
Los poderes de i son cíclicos, repitiéndose cada cuatro. Ver Ejemplo.

Factorización de\(i^{35}\)	\(i^{34}⋅i\)	\(i^{33}⋅i^2\)	\(i^{31}⋅i^4\)	\(i^{19}⋅i^{16}\)
Forma reducida	\({(i^2)}^{17}⋅i\)	\(i^{33}⋅(−1)\)	\(i^{31}⋅1\)	\(i^{19}⋅{(i^4)}^4\)
Forma simplificada	\({(−1)}^{17}⋅i\)	\(−i^{33}\)	\(i^{31}\)	\(i^{19}\)

Search

Text Color

Text Size

Margin Size

Font Type

Definición: Números imaginarios y complejos

Cómo: Dado un número imaginario, expresarlo en la forma estándar de un número complejo

Ejemplo\(\PageIndex{1}\): Expressing an Imaginary Number in Standard Form

Ejercicio\(\PageIndex{1}\)