5.5: Dividir polinomios

Última actualización
Guardar como PDF

Page ID: 116910

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Utilice la división larga para dividir polinomios.
Usa división sintética para dividir polinomios.

El exterior del Lincoln Memorial en Washington, D.C., es un gran sólido rectangular con$61.5$ metros de longitud (m), ancho$40$ m y alto$30$ m.$^1$

Podemos encontrar fácilmente el volumen usando geometría elemental.

\[\begin{align*} V&=l \; {\cdot} \; w \; {\cdot} \; h \\ &=61.5 \; {\cdot} \; 40 \; {\cdot} \; 30 \\ &=73,800 \end{align*}\]

Entonces el volumen es de metros$73,800$ cúbicos ($m^3$).

alt — Figura$\PageIndex{1}$: Lincoln Memorial, Washington, D.C. (crédito: Ron Cogswell, Flickr)

Supongamos que conocíamos el volumen, la longitud y la anchura. Podríamos dividirnos para encontrar la altura.

\[\begin{align*} h&=\dfrac{V}{l{\cdot}w} \\&=\dfrac{73,800}{61.5{\cdot}40} \\ &=30 \end{align*}\]

Como podemos confirmar a partir de las dimensiones anteriores, la altura es de 30 m. Podemos usar métodos similares para encontrar cualquiera de las dimensiones que faltan. También podemos usar el mismo método si alguna o todas las mediciones contienen expresiones variables. Por ejemplo, supongamos que el volumen de un sólido rectangular viene dado por el polinomio$3x^4−3x^3−33x^2+54x$. La longitud del sólido viene dada por$3x$; la anchura viene dada por$x−2$.

Para encontrar la altura del sólido, podemos utilizar la división polinómica, que es el foco de esta sección.

Uso de división larga para dividir polinomios

Estamos familiarizados con el algoritmo de división larga para la aritmética ordinaria. Comenzamos dividiendo en los dígitos del dividendo que tienen mayor valor posicional. Dividimos, multiplicamos, restamos, incluimos el dígito en la siguiente posición de valor posicional, y repetimos. Por ejemplo, dividamos 178 por 3 usando división larga.

$alt$

Otra forma de ver la solución es como una suma de partes. Esto debería parecer familiar, ya que es el mismo método utilizado para verificar la división en aritmética elemental.

\[\begin{align*} \text{dividend}&=(\text{divisor}{\cdot}\text{quotient})+\text{remainder} \\ 178&=(3{\cdot}59)+1 \\ &=177+1 \\ &=178\end{align*}\]

A esto lo llamamos el Algoritmo de División y lo discutiremos de manera más formal después de mirar un ejemplo.

La división de polinomios que contienen más de un término tiene similitudes con la división larga de números enteros. Podemos escribir un dividendo polinómico como producto del divisor y el cociente agregado al resto. Los términos de la división polinómica corresponden a los dígitos (y valores posicionales) de toda la división numérica. Este método nos permite dividir dos polinomios. Por ejemplo, si tuviéramos que dividir$2x^3−3x^2+4x+5$$x+2$ usando el algoritmo de división larga, se vería así:

\ [\ require {encerrar}\ begin {array} {rll}\ large x+2\ encerrar {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\ large\ text {Configurar el problema de división.}\\ [8pt]
\ large 2x^2\ hspace {5.45em} &\ qquad &\ grande2x^3\ texto {dividido por} x\ texto {es} 2x^2.\\ [-3pt]
\ grande x+2\ encerrar { longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\\ [8pt]
\ grande 2x^2\ hspace {5.45em} &\ qquad &\ [-3pt]
\ grande x+2\ encierra {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\\ [-3pt]
\ grande under\ línea {-\ izquierda (2x^3 + 4x^2\ derecha)}\ hespacio {4.9em} & \ qquad &\ large\ text {Multiplicar} x+2\ texto {por} 2x^2\ texto {y restar.}\\ [-3pt]
\ grande -7x^2+4x\ hspace {2.8em} &\ qquad &\ large\ text {Derribar el siguiente término.}\\ [8pt]

\ grande 2x^2 - 7x\ hspace {2.85em} &\ qquad &\ grande -7x^2\ texto {dividido por} x\ texto {es} -7x.\\ [-3pt]
\ grande x+2\ encierra {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\ [-3pt]
\ grande\ subrayado {-\ izquierda (2x^3 + 4x^2\ derecha)}\ hespacio {4.9em} &\ qquad &\\ [-3pt]
\ grande -7x^2+4x\ hspace {2.8em} &\ qquad &\\ [-3pt]
\ large\ underline {-\ left (-7x^2 - 14x\ right)}\ hspace {2.0em} &\ qquad &\ large\ text {Multiplicar} x+2\ text {por} -7x.\\ [-3pt]
\ grande 18x+5\ phantom {0} &\ qquad &\ large\ text {Restar y derribar el siguiente término.}\\ [8pt] grande

\ 2x^2 - 7x+18 &\ qquad &\ grande 18x\ texto {dividido por} x\ texto {es} 18.\\ [-3pt]
\ grande x+2\ encierra {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\ qquad &\\ [-3pt]
\ grande\ subrayado {-\ izquierda (2x^3 + 4x^2\ derecha)}\ hespacio {4.9em} &\ qquad y\\ [-3pt]
\ grande -7x^2+4x\ hspace {2.8 em} &\ qquad &\\ [-3pt]
\ grande\ subrayado {-\ izquierda (-7x^2 - 14x\ derecha)}\ hspace {2.0em} &\ qquad &\\ [-3pt]
\ grande 18x+\ phantom {0} 5 &\ qquad &\ [-3pt]
\ grande\ subrayado {-\ izquierda (18x + 36\ derecha)}\ hespacio {-0.45em} &\ qquad &\ grande\ text {Multiplicar} x+2\ texto {por} 18.\\ [-3pt]
\ large -31 &\ qquad &\ large\ text {Restar.}\\ [8pt]
\ end {array}\ nonumber\]

Hemos encontrado

\[\dfrac{2x^3−3x^2+4x+5}{x+2}=2x^2−7x+18−\dfrac{31}{x+2} \nonumber\]

\[ 2x^3−3x^2+4x+5=(x+2)(2x^2−7x+18)−31 \nonumber\]

Podemos identificar el dividendo, el divisor, el cociente y el resto.

Escribir el resultado de esta manera ilustra el Algoritmo de División.

El algoritmo de división

El Algoritmo de División establece que, dado un dividendo polinómico$f(x)$ y un divisor polinómico distinto de cero$d(x)$ donde el grado de$d(x)$ es menor o igual al grado de$f(x)$, existen polinomios únicos$q(x)$ y$r(x)$ tales que

\[f(x)=d(x)q(x)+r(x)\]

$q(x)$es el cociente y$r(x)$ es el resto. El resto es igual a cero o tiene grado estrictamente menor que$d(x)$.

Si$r(x)=0$, entonces se$d(x)$ divide uniformemente en$f(x)$. Esto quiere decir que, en este caso, ambos$d(x)$ y$q(x)$ son factores de$f(x)$.

Dado un polinomio y un binomio, usar división larga para dividir el polinomio por el binomio

Configurar el problema de división.
Determinar el primer término del cociente dividiendo el término principal del dividendo por el término principal del divisor.
Multiplique la respuesta por el divisor y escríbala por debajo de los términos similares del dividendo.
Restar el binomio inferior del binomio superior.
Derribar el siguiente plazo del dividendo.
Repita los pasos 2—5 hasta llegar al último término del dividendo.
Si el resto es distinto de cero, exprese como fracción usando el divisor como denominador.

Ejemplo$\PageIndex{1}$: Using Long Division to Divide a Second-Degree Polynomial

Dividir$5x^2+3x−2$ por$x+1$.

Solución

$alt$

El cociente es$5x−2$. El resto es 0. Escribimos el resultado como

\[\dfrac{5x^2+3x−2}{x+1}=5x−2 \nonumber\]

\[5x^2+3x−2=(x+1)(5x−2) \nonumber\]

Análisis

Este problema de división tuvo un resto de 0. Esto nos dice que el dividendo se divide equitativamente por el divisor, y que el divisor es un factor del dividendo.

Ejemplo$\PageIndex{2}$: Using Long Division to Divide a Third-Degree Polynomial

Dividir$6x^3+11x^2−31x+15$ por$3x−2$.

Solución

\ [\ require {encerrar}\ begin {array} {rll}
\ large 2x^2 +\ phantom {0} 5x-\ phantom {0} 7 &\ qquad &\ large 6x^3\ text {dividido por} 3x\ text {es} 2x^2.\\ [-3pt]
\ grande 3x-2\ encierra {longdiv} {6x^3+11x^2-31x+15} &\ qquad &\\ [-3pt]
\ grande\ subrayado {-\ izquierda (6x^3 - 4x^2 \ derecha)}\ hespacio {5.8em} &\ qquad &\ grande\ texto {Multiplicar} 3x-2\ texto {por} 2x^2.\\ [-3pt]
\ grande 15x^2-31x\ hspace {3.0em} &\ qquad &\ grande\ texto {Restar. Derribar siguiente término.} 15x^2\ texto {dividido por} 3x\ texto {es} 5x.\\ [-3pt]
\ grande\ subrayado {-\ izquierda (15x^2 - 10x\ derecha)}\ hspace {2.5em} &\ qquad &\ grande\ texto {Multiplicar} 3x-2\ texto {por} 5x.\\ [-3pt]
\ grande -21x+15\ hspace {0.5em} &\ qquad &\ large\ text {Restar. Derribar siguiente término.} -21x\ texto {dividido por} 3x\ texto {es} -7.\\ [-3pt]
\ grande\ subrayado {-\ izquierda (-21x + 14\ derecha)}\ hspace {0.1em} &\ qquad &\ large\ text {Multiplicar} 3x-2\ texto {por} -7.\\ [-3pt]
\ grande 1\ hspace {0.5em} &\ qquad &\ large\ text {Resta. El resto es 1.}\\ [8pt]
\ end {array}\ nonumber\]

Hay un resto de 1. Podemos expresar el resultado como:

\[\dfrac{6x^3+11x^2−31x+15}{3x−2}=2x^2+5x−7+\dfrac{1}{3x−2} \nonumber\]

Análisis

Podemos verificar nuestro trabajo usando el Algoritmo de División para reescribir la solución. Después multiplicar.

\[(3x−2)(2x^2+5x−7)+1=6x^3+11x^2−31x+15 \nonumber\]

Aviso, a medida que escribimos nuestro resultado,

el dividendo es$6x^3+11x^2−31x+15$
el divisor es$3x−2$
el cociente es$2x^2+5x−7$
el resto es$1$

¡Pruébalo! $\PageIndex{2}$

Dividir$16x^3−12x^2+20x−3$ por$4x+5$.

Solución: $4x^2−8x+15−\dfrac{78}{4x+5}$

Uso de división sintética para dividir polinomios

Como hemos visto, la larga división de polinomios puede implicar muchos pasos y ser bastante engorrosa. La división sintética es un método abreviado de dividir polinomios para el caso especial de dividir por un factor lineal cuyo coeficiente principal es$1.$

Para ilustrar el proceso, recordemos el ejemplo al inicio de la sección.

Dividir$2x^3−3x^2+4x+5$$x+2$ usando el algoritmo de división larga.

La forma final del proceso se veía así:

\ [\ require {encerrar}\ begin {array} {rl}\ grande 2x^2 - 7x+18 &\\ [-3pt]
\ grande x+2\ encerrar {longdiv} {2x^3-3x^2+4x+5\ phantom {0}} &\\ [-3pt]
\ grande\ subrayado {-\ izquierda (2x^3 + 4x^2\ derecha)}\ hspace {4.9em} &\\ [-3pt]
\ grande -7x^2+4x\ hspace {2.8em} &\\ [-3pt]
\ grande\ subrayado {-\ izquierda (-7x^2 - 14x\ derecha)}\ hspace {2.0em} &\\ [-3pt]
\ grande 18x+\ phantom {0} 5 &\\ [-3pt]
\ grande\ subrayado {-\ izquierda (18x + 36\ derecha)}\ hespacio {-0.45em} &\\ [-3pt]
\ grande -31 &\ [8pt]
\ end {array}\ nonumber \]

Hay mucha repetición en la tabla. Si no escribimos las variables sino, en cambio, alineamos sus coeficientes en columnas bajo el signo de división y además eliminamos los productos parciales, ya tenemos una versión más sencilla de todo el problema.

$alt$

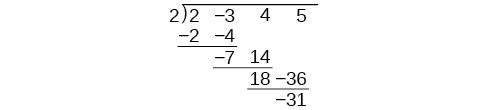
La división sintética conlleva esta simplificación incluso algunos pasos más. Contraer la mesa moviendo cada una de las filas hacia arriba para llenar cualquier lugar vacante. También, en lugar de dividir por 2, como lo haríamos en división de números enteros, luego multiplicando y restando el producto medio, cambiamos el signo del “divisor” a —2, multiplicamos y sumamos. El proceso inicia bajando el coeficiente principal.

$alt$

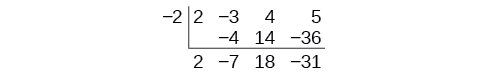
Luego lo multiplicamos por el “divisor” y agregamos, repitiendo este proceso columna por columna, hasta que no queden entradas. La fila inferior representa los coeficientes del cociente; la última entrada de la fila inferior es el resto. En este caso, el cociente es$2x^2–7x+18$ y el resto es$–31.$ El proceso se hará más claro en Ejemplo$\PageIndex{3}$.

División Sintética

La división sintética es un atajo que se puede utilizar cuando el divisor es un binomio en la forma$x−k$. En la división sintética, solo se utilizan los coeficientes en el proceso de división.

Dados dos polinomios, use división sintética para dividir

Escribir$k$ para el divisor.
Escribir los coeficientes del dividendo.
Bajar el coeficiente de plomo.
Multiplique el coeficiente de plomo por$k$. Escribe el producto en la siguiente columna.
Agregar los términos de la segunda columna.
Multiplique el resultado por$k$. Escribe el producto en la siguiente columna.
Repita los pasos 5 y 6 para las columnas restantes.
Usa los números inferiores para escribir el cociente. El número en la última columna es el resto y tiene grado 0, el siguiente número de la derecha tiene grado 1, el siguiente número de la derecha tiene grado 2, y así sucesivamente.

Ejemplo$\PageIndex{3}$: Using Synthetic Division to Divide a Second-Degree Polynomial

Usa división sintética para dividir$5x^2−3x−36$ por$x−3$.

Solución

Comience por establecer la división sintética. Escribir$k$ y los coeficientes.

$alt$

Bajar el coeficiente de plomo. Multiplique el coeficiente de plomo por$k$.

$alt$

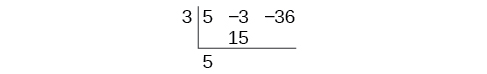
Continúa sumando los números en la segunda columna. Multiplica el número resultante por$k$ .Escribe el resultado en la siguiente columna. Después suma los números en la tercera columna.

$alt$

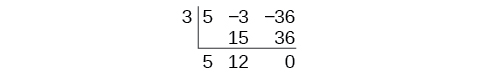
El resultado es$5x+12$. El resto es 0. Así$x−3$ es un factor del polinomio original.

Análisis

Al igual que con la división larga, podemos verificar nuestro trabajo multiplicando el cociente por el divisor y sumando el resto.

\[(x−3)(5x+12)+0=5x^2−3x−36 \nonumber\]

Ejemplo$\PageIndex{4}$: Using Synthetic Division to Divide a Third-Degree Polynomial

Usa división sintética para dividir$4x^3+10x^2−6x−20$ por$x+2$.

Solución

El divisor binomial es$x+2$ así$k=−2$. Sumar cada columna, multiplicar el resultado por —2, y repetir hasta llegar a la última columna.

\ [\ large {\ begin {array} {c} -2\\\\\
\ end {array}} {\ begin
{align*} &\\ [0pt]
& {\ begin {array} {r|}\\ [0pt]\\ [0pt]
\ [0pt]\ end {array}}\\ [1pt]
&\\ [2pt] &\ end {align*}}\! \!
{\ begin {array} {rrrr}
1 & -1 & -11 & 18\\
& 2 & 2 & -18\
\ hline 1 & 1 & -9 & 0
\ end {array}}
\ nonumber\]

El resultado es$4x^2+2x−10$.

El resto es 0. Así,$x+2$ es un factor de$4x^3+10x^2−6x−20$.

Análisis

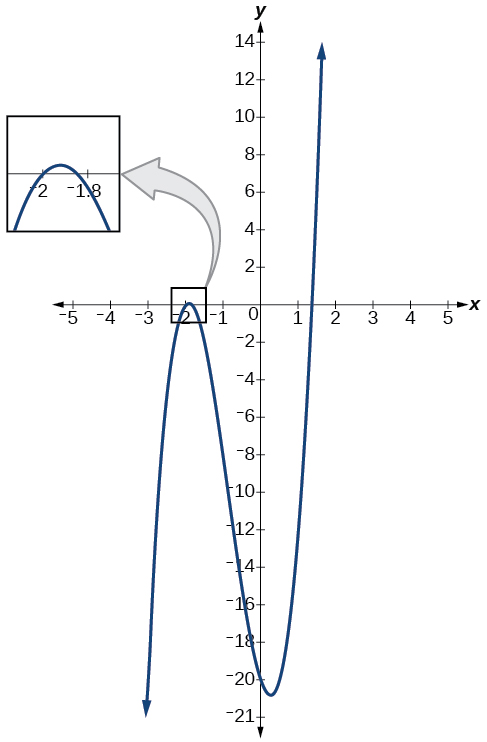
La gráfica de la función polinómica$f(x)=4x^3+10x^2−6x−20$ en la Figura$\PageIndex{2}$ muestra un cero at$x=k=−2$. Esto confirma que$x+2$ es un factor de$4x^3+10x^2−6x−20$.

Ejemplo$\PageIndex{5}$: Using Synthetic Division to Divide a Fourth-Degree Polynomial

Usa división sintética para dividir$−9x^4+10x^3+7x^2−6$ por$x−1$.

Solución

Observe que no hay$x$ -plazo. Usaremos un cero como coeficiente para ese término.

\ [\ large {\ begin {array} {c} 1\\\\\\
\ end {array}}
{\ begin {align*} &\\ [0pt]
& {\ begin {array} {r|}\\ [0pt]\
\ [0pt]\ [0pt]\ end {array}}\\ [1pt]
&\\ [2pt] &\ end {align*}}\! \!
{\ begin {array} {rrrrr}
-9 & 10 & 7 & 0 &-6\\
& -9 & 1 & 8 & 8\
\ hline -9 & 1& 8 & 8 & 2
\ end {array}}
\ nonumber\]

El resultado es$−9x^3+x^2+8x+8+\dfrac{2}{x−1}$.

¡Pruébalo! $\PageIndex{3}$

Usa división sintética para dividir$3x^4+18x^3−3x+40$ por$x+7$.

Solución: $3x^3−3x^2+21x−150+\dfrac{1090}{x+7}$

Uso de la División Polinómica para Resolver Problemas de Aplicación

La división polinómica se puede utilizar para resolver una variedad de problemas de aplicación que involucran expresiones para área y volumen. Miramos una aplicación al inicio de esta sección. Ahora vamos a resolver ese problema en el siguiente ejemplo.

Ejemplo$\PageIndex{6}$: Using Polynomial Division in an Application Problem

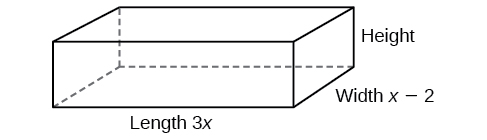
El volumen de un sólido rectangular viene dado por el polinomio$3x^4−3x^3−33x^2+54x$. La longitud del sólido viene dada por$3x$ y la anchura viene dada por$x−2$. Encuentra la altura$h$ del sólido.

Solución

Hay algunas formas de abordar este problema. Necesitamos dividir la expresión para el volumen del sólido por las expresiones para el largo y ancho. Vamos a crear un boceto como en la Figura$\PageIndex{3}$. Dejar$h$ igualar la altura de la caja.

Ahora podemos escribir una ecuación sustituyendo los valores conocidos en la fórmula por el volumen de un sólido rectangular.

\[\begin{align*} V&=l{\cdot}w{\cdot}h \\ 3x^4−3x^3−33x^2+54x&=3x{\cdot}(x−2){\cdot}h \end{align*}\]

Para resolver$h$, primero divide ambos lados por$3x$.

\[\dfrac{3x{\cdot}(x−2){\cdot}h}{3x}=\dfrac{3x^4−3x^3−33x^2+54x}{3x} \nonumber\]

\[(x-2)h=\dfrac{x^3-x^2-11x+18}{x-2} \nonumber\]

Ahora resuelve para$h$ usar división sintética.

\[h=\dfrac{x^3−x^2−11x+18}{x−2} \nonumber\]

El cociente es$x^2+x−9$ y el resto es$0.$ La altura del sólido es$x^2+x−9$.

¡Pruébalo! $\PageIndex{4}$

El área de un rectángulo viene dada por$3x^3+14x^2−23x+6$. El ancho del rectángulo viene dado por$x+6$. Encuentra una expresión para la longitud del rectángulo.

Solución: $3x^2−4x+1$

Ecuaciones Clave

Algoritmo$f(x)=d(x)q(x)+r(x)$ de división$q(x){\neq}0$

Conceptos clave

La división polinómica larga se puede utilizar para dividir un polinomio por cualquier polinomio con igual o menor grado.
El algoritmo de división nos dice que un dividendo polinómico puede escribirse como producto del divisor y el cociente agregado al resto.
La división sintética es un atajo que se puede utilizar para dividir un polinomio por un binomio en la forma$x−k.$
La división polinómica se puede utilizar para resolver problemas de aplicación, incluyendo área y volumen.

Notas al pie

$^1$Servicio de Parques Nacionales. “Lincoln Memorial Building Statistics.” www.nps.gov/linc/historycultu... statistics.htm. Accedido 04/3/2014

Glosario

algoritmo de división

dado un dividendo polinómico$f(x)$ y un divisor polinómico distinto de cero$d(x)$ donde el grado de$d(x)$ es menor o igual al grado de$f(x)$, existen polinomios únicos$q(x)$ y$r(x)$ tal que$f(x)=d(x)q(x)+r(x)$ donde$q(x)$ está el cociente y$r(x)$ es el resto. El resto es igual a cero o tiene grado estrictamente menor que$d(x)$.

división sintética

un método de atajo que se puede utilizar para dividir un polinomio por un binomio de la forma$x−k$

Search

Text Color

Text Size

Margin Size

Font Type