6.4: Funciones logarítmicas
- Page ID
- 116955
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Convertir de forma logarítmica a exponencial.
- Convertir de forma exponencial a logarítmica.
- Evaluar logaritmos.
- Utilizar logaritmos comunes.
- Utilizar logaritmos naturales.
En 2010, un gran terremoto azotó Haití, destruyendo o dañando más de 285 mil viviendas. Un año después, otro terremoto más fuerte devastó Honshu, Japón, destruyendo o dañando más de 332 mil edificios, como los que se muestran en la Figura\(\PageIndex{1}\). A pesar de que ambos causaron daños sustanciales, el sismo de 2011 fue 100 veces más fuerte que el sismo en Haití. ¿Cómo lo sabemos? Las magnitudes de los sismos se miden en una escala conocida como Escala de Richter. El sismo haitiano registró un 7.0 en la Escala Richter mientras que el sismo japonés registró un 9.0.

Figura\(\PageIndex{1}\): Devastación del terremoto del 11 de marzo de 2011 en Honshu, Japón. (crédito: Daniel Pierce).
La Escala Richter es una escala logarítmica de base diez. Es decir, un sismo de magnitud no\(8\) es el doble de grande que un sismo de magnitud\(4\). Es
\[10^{8−4}=10^4=10,000 \nonumber\]
tiempos tan grandes! En esta lección, investigaremos la naturaleza de la Escala de Richter y la función de base diez de la que depende.
Conversión de forma logarítmica a exponencial
Para analizar la magnitud de los sismos o comparar las magnitudes de dos sismos diferentes, necesitamos poder convertir entre forma logarítmica y exponencial. Por ejemplo, supongamos que la cantidad de energía liberada de un sismo fue 500 veces mayor que la cantidad de energía liberada de otro. Queremos calcular la diferencia de magnitud. La ecuación que representa este problema es\(10^x=500\), donde\(x\) representa la diferencia de magnitudes en la Escala de Richter. ¿Cómo lo resolveríamos\(x\)?
Aún no hemos aprendido un método para resolver ecuaciones exponenciales. Ninguna de las herramientas algebraicas discutidas hasta el momento es suficiente para resolver\(10^x=500\). Eso lo sabemos\({10}^2=100\) y\({10}^3=1000\), por lo que es claro que\(x\) debe haber algún valor entre 2 y 3, ya que\(y={10}^x\) va en aumento. Podemos examinar una gráfica, como en la Figura\(\PageIndex{1}\), para estimar mejor la solución.
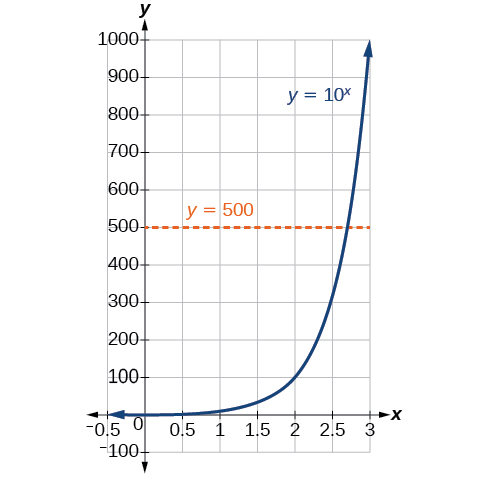
Figura\(\PageIndex{2}\)
Estimar a partir de una gráfica, sin embargo, es impreciso. Para encontrar una solución algebraica, debemos introducir una nueva función. Observe que la gráfica de la Figura\(\PageIndex{2}\) pasa la prueba de línea horizontal. La función exponencial\(y=b^x\) es uno a uno, por lo que su inversa, también\(x=b^y\) es una función. Como es el caso de todas las funciones inversas, simplemente intercambiamos\(x\)\(y\) y resolvemos\(y\) para encontrar la función inversa. Para representar\(y\) como una función de\(x\), utilizamos una función logarítmica de la forma\(y={\log}_b(x)\). El\(b\) logaritmo base de un número es el exponente por el cual debemos subir\(b\) para obtener ese número.
Leemos una expresión logarítmica como, “El logaritmo con base\(b\) de\(x\) es igual a”\(y\), o, simplificado, “log base\(b\) de\(x\) es”\(y\). También podemos decir, “\(b\)elevado al poder de\(y\) es”\(x\), porque los registros son exponentes. Por ejemplo, el\(2\) logaritmo base de\(32\) es\(5\), porque\(5\) es el exponente al que debemos aplicar\(2\) para obtener\(32\). Ya que\(2^5=32\), podemos escribir\({\log}_232=5\). Leemos esto como “base\(2\) de registro de\(32\) es”\(5\).
Podemos expresar la relación entre la forma logarítmica y su forma exponencial correspondiente de la siguiente manera:
\[\begin{align} \log_b(x)=y\Leftrightarrow b^y=x, b> 0, b\neq 1 \end{align}\]
Tenga en cuenta que la base siempre\(b\) es positiva.
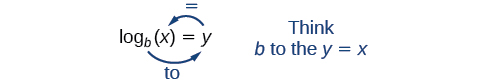
Debido a que el logaritmo es una función, se escribe más correctamente como\(\log_b(x)\), usando paréntesis para denotar la evaluación de funciones, tal como lo haríamos con\(f(x)\). Sin embargo, cuando la entrada es una sola variable o número, es común ver los paréntesis caídos y la expresión escrita sin paréntesis, como\(\log_bx\). Tenga en cuenta que muchas calculadoras requieren paréntesis alrededor del\(x\).
Podemos ilustrar la notación de logaritmos de la siguiente manera:

Observe que, comparando la función logaritmo y la función exponencial, se conmutan la entrada y la salida. Esto significa\(y={\log}^b(x)\) y\(y=b^x\) son funciones inversas.
Una base logaritmo\(b\) de un número positivo\(x\) satisface la siguiente definición.
Para\(x>0\),\(b>0\),\(b≠1\),
\[\begin{align} y={\log}_b(x)\text{ is equivalent to } b^y=x \end{align}\]
donde,
- leemos\({\log}_b(x)\) como, “el logaritmo con base\(b\) de\(x\)” o la “base logarítmica\(b\) de”\(x\).
- el logaritmo\(y\) es el exponente al que se\(b\) debe elevar para llegar\(x\).
Además, dado que las funciones logarítmica y exponencial cambian los\(y\) valores\(x\) y, el dominio y el rango de la función exponencial se intercambian por la función logarítmica. Por lo tanto,
- el dominio de la función logaritmo con base\(b\) es\((0,\infty)\).
- el rango de la función logaritmo con base\(b\) es\((−\infty,\infty)\).
No. Debido a que la base de una función exponencial es siempre positiva, ningún poder de esa base puede ser nunca negativo. Nunca podremos tomar el logaritmo de un número negativo. Además, no podemos tomar el logaritmo de cero. Las calculadoras pueden generar un log de un número negativo cuando están en modo complejo, pero el log de un número negativo no es un número real.
- Examinar la ecuación\(y={\log}_bx\) e identificar\(b\),\(y\), y\(x\).
- Reescribir\({\log}_bx=y\) como\(b^y=x\).
Escribe las siguientes ecuaciones logarítmicas en forma exponencial.
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
- \({\log}_3(9)=2\)
Solución
Primero, identificar los valores de\(b\),\(y\), y\(x\). Después, escribe la ecuación en la forma\(b^y=x\).
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\)
Aquí,\(b=6\),\(y=\dfrac{1}{2}\), y\(x=\sqrt{6}\). Por lo tanto, la ecuación\({\log}_6(\sqrt{6})=\dfrac{1}{2}\) es equivalente a
\(6^{\tfrac{1}{2}}=\sqrt{6}\)
- \({\log}_3(9)=2\)
Aquí,\(b=3\),\(y=2\), y\(x=9\). Por lo tanto, la ecuación\({\log}_3(9)=2\) es equivalente a
\(3^2=9\)
Escribe las siguientes ecuaciones logarítmicas en forma exponencial.
- \({\log}_{10}(1,000,000)=6\)
- \({\log}_5(25)=2\)
- Contestar a
-
\({\log}_{10}(1,000,000)=6\)es equivalente a\({10}^6=1,000,000\)
- Respuesta b
-
\({\log}_5(25)=2\)es equivalente a\(5^2=25\)
Conversión de forma exponencial a logarítmica
Para convertir de exponentes a logaritmos, seguimos los mismos pasos a la inversa. Identificamos la base\(b\), exponente\(x\) y salida\(y\). Entonces escribimos\(x={\log}_b(y)\).
Escribe las siguientes ecuaciones exponenciales en forma logarítmica.
- \(2^3=8\)
- \(5^2=25\)
- \({10}^{−4}=\dfrac{1}{10,000}\)
Solución
Primero, identificar los valores de\(b\),\(y\), y\(x\). Después, escribe la ecuación en la forma\(x={\log}_b(y)\).
- \(2^3=8\)
Aquí,\(b=2\),\(x=3\), y\(y=8\). Por lo tanto, la ecuación\(2^3=8\) es equivalente a\({\log}_2(8)=3\).
- \(5^2=25\)
Aquí,\(b=5\),\(x=2\), y\(y=25\). Por lo tanto, la ecuación\(5^2=25\) es equivalente a\({\log}_5(25)=2\).
- \({10}^{−4}=\dfrac{1}{10,000}\)
Aquí,\(b=10\),\(x=−4\), y\(y=\dfrac{1}{10,000}\). Por lo tanto, la ecuación\({10}^{−4}=\dfrac{1}{10,000}\) es equivalente a\({\log}_{10} \left (\dfrac{1}{10,000} \right )=−4\).
Escribe las siguientes ecuaciones exponenciales en forma logarítmica.
- \(3^2=9\)
- \(5^3=125\)
- \(2^{−1}=\dfrac{1}{2}\)
- Contestar a
-
\(3^2=9\)es equivalente a\({\log}_3(9)=2\)
- Respuesta b
-
\(5^3=125\)es equivalente a\({\log}_5(125)=3\)
- Respuesta c
-
\(2^{−1}=\dfrac{1}{2}\)es equivalente a\({\log}_2 \left (\dfrac{1}{2} \right )=−1\)
Evaluando logaritmos
Conocer los cuadrados, cubos y raíces de los números nos permite evaluar mentalmente muchos logaritmos. Por ejemplo, considere\({\log}_28\). Nos preguntamos: “¿A qué exponente\(2\) se debe elevar para conseguir 8?” Porque ya lo sabemos\(2^3=8\), se deduce de eso\({\log}_28=3\).
Ahora considera resolver\({\log}_749\) y\({\log}_327\) mentalmente.
- Nos preguntamos: “¿A qué exponente\(7\) se debe elevar para poder llegar\(49\)?” Lo sabemos\(7^2=49\). Por lo tanto,\({\log}_749=2\)
- Nos preguntamos: “¿A qué exponente\(3\) se debe elevar para poder llegar\(27\)?” Lo sabemos\(3^3=27\). Por lo tanto,\(\log_{3}27=3\)
Incluso algunos logaritmos aparentemente más complicados pueden ser evaluados sin una calculadora. Por ejemplo, evaluemos\(\log_{\ce{2/3}} \frac{4}{9}\) mentalmente.
- Nos preguntamos: “¿A qué exponente\(\ce{2/3}\) se debe elevar para poder llegar\(\ce{4/9}\)? ” Sabemos\(2^2=4\) y\(3^2=9\), por lo\[{\left(\dfrac{2}{3} \right )}^2=\dfrac{4}{9}. \nonumber\] tanto,\[{\log}_{\ce{2/3}} \left (\dfrac{4}{9} \right )=2. \nonumber\]
- Reescribir el argumento\(x\) como un poder de\(b\):\(b^y=x\).
- Utilizar conocimientos previos de poderes de\(b\) identificación\(y\) preguntando: “¿A qué exponente\(b\) se debe elevar para poder llegar\(x\)?”
Resuelve\(y={\log}_4(64)\) sin usar una calculadora.
Solución
Primero reescribimos el logaritmo en forma exponencial:\(4^y=64\). A continuación, preguntamos: “¿A qué exponente\(4\) se debe elevar para poder llegar\(64\)?”
Sabemos
\(4^3=64\)
Por lo tanto,
\({\log}_4(64)=3\)
Resuelve\(y={\log}_{121}(11)\) sin usar una calculadora.
- Contestar
-
\({\log}_{121}(11)=\dfrac{1}{2}\)(recordando que\(\sqrt{121}={(121)}^{\tfrac{1}{2}}=11)\)
Evaluar\(y={\log}_3 \left (\dfrac{1}{27} \right )\) sin usar una calculadora.
Solución
Primero reescribimos el logaritmo en forma exponencial:\(3^y=\dfrac{1}{27}\). A continuación, preguntamos: “¿A qué exponente\(3\) se debe elevar para poder llegar\(\dfrac{1}{27}\)?”
Sabemos\(3^3=27\), pero ¿qué debemos hacer para conseguir lo recíproco,\(\dfrac{1}{27}\)? Recordemos de trabajar con exponentes que\(b^{−a}=\dfrac{1}{b^a}\). Utilizamos esta información para escribir
\[\begin{align*} 3^{-3}&= \dfrac{1}{3^3}\\ &= \dfrac{1}{27} \end{align*}\]
Por lo tanto,\({\log}_3 \left (\dfrac{1}{27} \right )=−3\).
Evaluar\(y={\log}_2 \left (\dfrac{1}{32} \right )\) sin usar una calculadora.
- Contestar
-
\({\log}_2 \left (\dfrac{1}{32} \right )=−5\)
Uso de logaritmos comunes
A veces podemos ver un logaritmo escrito sin base. En este caso, suponemos que la base es\(10\). En otras palabras, la expresión\(\log(x)\) significa\({\log}_{10}(x)\). Llamamos a un\(-10\) logaritmo base un logaritmo común. Se utilizan logaritmos comunes para medir la Escala de Richter mencionada al inicio de la sección. Las escalas para medir el brillo de las estrellas y el pH de ácidos y bases también utilizan logaritmos comunes.
Un logaritmo común es un logaritmo con base\(10\). Escribimos\({\log}_{10}(x)\) simplemente como\(\log(x)\). El logaritmo común de un número positivo\(x\) satisface la siguiente definición.
Para\(x>0\),
\[\begin{align} y={\log}(x)\text{ is equivalent to } {10}^y=x \end{align}\]
Leemos\(\log(x)\) como, “el logaritmo con base\(10\) de\(x\)” o “base logarítmica\(10\) de”\(x\).
El logaritmo\(y\) es el exponente al que se\(10\) debe elevar para llegar\(x\).
- Reescribir el argumento\(x\) como un poder de\(10\):\({10}^y=x\).
- Utilizar conocimientos previos de poderes de\(10\) para identificar\(y\) preguntando: “¿A qué exponente\(10\) se debe elevar para poder llegar\(x\)?”
Evaluar\(y=\log(1000)\) sin usar una calculadora.
Solución
Primero reescribimos el logaritmo en forma exponencial:\({10}^y=1000\). A continuación, preguntamos: “¿A qué exponente\(10\) se debe elevar para poder llegar\(1000\)?” Sabemos
\({10}^3=1000\)
Por lo tanto,\(\log(1000)=3\).
Evaluar\(y=\log(1,000,000)\).
- Contestar
-
\(\log(1,000,000)=6\)
- Pulse [LOG].
- Ingresa el valor dado para\(x\), seguido de [)].
- Pulse [ENTER].
Evalúa\(y=\log(321)\) a cuatro decimales usando una calculadora.
Solución
- Pulse [LOG].
- Ingresa 321, seguido de [)].
- Pulse [ENTER].
Redondeo a cuatro decimales,\(\log(321)≈2.5065\).
Análisis
Tenga en cuenta eso\({10}^2=100\) y eso\({10}^3=1000\). Ya que\(321\) es entre\(100\) y\(1000\), sabemos que\(\log(321)\) debe ser entre\(\log(100)\) y\(\log(1000)\). Esto nos da lo siguiente:
\(100<321<1000\)
\(2<2.5065<3\)
Evalúa\(y=\log(123)\) a cuatro decimales usando una calculadora.
- Contestar
-
\(\log(123)≈2.0899\)
La cantidad de energía liberada de un sismo fue\(500\) veces mayor que la cantidad de energía liberada de otro. La ecuación\({10}^x=500\) representa esta situación, donde\(x\) está la diferencia de magnitudes en la Escala de Richter. A la milésima más cercana, ¿cuál era la diferencia de magnitudes?
Solución
Comenzamos por reescribir la ecuación exponencial en forma logarítmica.
\({10}^x=500\)
\(\log(500)=x\)Utilice la definición del registro común.
A continuación evaluamos el logaritmo usando una calculadora:
- Pulse [LOG].
- Entrar\(500\), seguido de [)].
- Pulse [ENTER].
- A la milésima más cercana,\(\log(500)≈2.699\).
La diferencia en magnitudes fue de aproximadamente\(2.699\).
La cantidad de energía liberada de un sismo fue\(8,500\) veces mayor que la cantidad de energía liberada de otro. La ecuación\({10}^x=8500\) representa esta situación, donde\(x\) está la diferencia de magnitudes en la Escala de Richter. A la milésima más cercana, ¿cuál era la diferencia de magnitudes?
- Contestar
-
La diferencia en magnitudes fue de aproximadamente\(3.929\).
Uso de logaritmos naturales
La base más utilizada para logaritmos es\(e\). Los\(e\) logaritmos base son importantes en el cálculo y algunas aplicaciones científicas; se denominan logaritmos naturales. El\(e\) logaritmo base,\({\log}_e(x)\), tiene su propia notación,\(\ln(x)\). La mayoría de los valores de solo se\(\ln(x)\) pueden encontrar usando una calculadora. La mayor excepción es que, debido a que el logaritmo de\(1\) está siempre\(0\) en cualquier base,\(\ln1=0\). Para otros logaritmos naturales, podemos utilizar la\(\ln\) clave que se puede encontrar en la mayoría de las calculadoras científicas. También podemos encontrar el logaritmo natural de cualquier potencia de\(e\) usar la propiedad inversa de logaritmos.
Un logaritmo natural es un logaritmo con base\(e\). Escribimos\({\log}_e(x)\) simplemente como\(\ln(x)\). El logaritmo natural de un número positivo\(x\) satisface la siguiente definición.
Para\(x>0\),
\(y=\ln(x)\)es equivalente a\(e^y=x\)
Leemos\(\ln(x)\) como, “el logaritmo con base\(e\) de\(x\)” o “el logaritmo natural de”\(x\).
El logaritmo\(y\) es el exponente al que se\(e\) debe elevar para llegar\(x\).
Ya que las funciones\(y=e^x\) y\(y=\ln(x)\) son funciones inversas,\(\ln(e^x)=x\) para todos\(x\) y\(e^{\ln (x)}=x\) para\(x>0\).
- Presione [LN].
- Ingresa el valor dado para\(x\), seguido de [)].
- Pulse [ENTER].
Evalúa\(y=\ln(500)\) a cuatro decimales usando una calculadora.
Solución
- Presione [LN].
- Entrar\(500\), seguido de [)].
- Pulse [ENTER].
Redondeo a cuatro decimales,\(\ln(500)≈6.2146\)
Evaluar\(\ln(−500)\).
- Contestar
-
No es posible tomar el logaritmo de un número negativo en el conjunto de números reales.
Acceda a este recurso en línea para obtener instrucción adicional y práctica con logaritmos.
Ecuaciones Clave
| Definición de la función logarítmica | Para\(x>0\),\(b>0\),\(b≠1\),\(y={\log}_b(x)\) si y sólo si\(b^y=x\). |
| Definición del logaritmo común | Para\(x>0\),\(y=\log(x)\) si y solo si\({10}^y=x\). |
| Definición del logaritmo natural | Para\(x>0\),\(y=\ln(x)\) si y solo si\(e^y=x\). |
Conceptos clave
- La inversa de una función exponencial es una función logarítmica, y la inversa de una función logarítmica es una función exponencial.
- Las ecuaciones logarítmicas se pueden escribir en una forma exponencial equivalente, utilizando la definición de un logaritmo. Ver Ejemplo\(\PageIndex{1}\).
- Las ecuaciones exponenciales se pueden escribir en su forma logarítmica equivalente usando la definición de un logaritmo Ver Ejemplo\(\PageIndex{2}\).
- Las funciones logarítmicas con base\(b\) pueden evaluarse mentalmente utilizando conocimientos previos de poderes de\(b\). Ver Ejemplo\(\PageIndex{3}\) y Ejemplo\(\PageIndex{4}\).
- Los logaritmos comunes pueden evaluarse mentalmente utilizando conocimientos previos de poderes de\(10\). Ver Ejemplo\(\PageIndex{5}\).
- Cuando los logaritmos comunes no se pueden evaluar mentalmente, se puede utilizar una calculadora. Ver Ejemplo\(\PageIndex{6}\).
- Los problemas exponenciales del mundo real con base\(10\) pueden reescribirse como un logaritmo común y luego evaluarse usando una calculadora. Ver Ejemplo\(\PageIndex{7}\).
- Los logaritmos naturales pueden ser evaluados usando una calculadora Ejemplo\(\PageIndex{8}\).


