6.9: Ajuste de modelos exponenciales a los datos

Objetivos de aprendizaje

• Construye un modelo exponencial a partir de datos.
• Construir un modelo logarítmico a partir de datos.
• Construir un modelo logístico a partir de datos.

En secciones anteriores de este capítulo, o bien se nos dio una función explícitamente para graficar o evaluar, o bien se nos dio un conjunto de puntos que se garantizaba que estaban en la curva. Luego usamos álgebra para encontrar la ecuación que se ajustaba exactamente a los puntos. En esta sección, utilizamos una técnica de modelado llamada análisis de regresión para encontrar una curva que modele los datos recopilados de observaciones del mundo real. Con el análisis de regresión, no esperamos que todos los puntos se encuentren perfectamente en la curva. La idea es encontrar un modelo que mejor se ajuste a los datos. Entonces usamos el modelo para hacer predicciones sobre eventos futuros.

No se confunda por la palabra modelo. En matemáticas, a menudo usamos los términos función, ecuación y modelo indistintamente, a pesar de que cada uno tiene su propia definición formal. El término modelo se usa típicamente para indicar que la ecuación o función se aproxima a una situación del mundo real.

Nos concentraremos en tres tipos de modelos de regresión en esta sección: exponencial, logarítmico y logístico. Haber trabajado ya con cada una de estas funciones nos da una ventaja. Conocer sus definiciones formales, el comportamiento de sus gráficas y algunas de sus aplicaciones del mundo real nos da la oportunidad de profundizar en nuestra comprensión. A medida que se presenta cada modelo de regresión, se incluyen características clave y definiciones de su función asociada para su revisión. Tómese un momento para repensar cada una de estas funciones, reflexionar sobre el trabajo que hemos realizado hasta ahora y luego explorar las formas en que se utiliza la regresión para modelar fenómenos del mundo real.

Construyendo un Modelo Exponencial a partir de Datos

Como hemos aprendido, hay multitud de situaciones que pueden modelarse mediante funciones exponenciales, como el crecimiento de la inversión, la desintegración radiactiva, los cambios de presión atmosférica y las temperaturas de un objeto de enfriamiento. ¿Qué tienen en común estos fenómenos? Por un lado, todos los modelos aumentan o disminuyen a medida que avanza el tiempo. Pero esa no es toda la historia. Es la forma en que los datos aumentan o disminuyen lo que nos ayuda a determinar si se modela mejor mediante una ecuación exponencial. Conocer el comportamiento de las funciones exponenciales en general nos permite reconocer cuándo usar la regresión exponencial, así que revisemos el crecimiento exponencial y la decadencia.

Recordemos que las funciones exponenciales tienen la forma\(y=ab^x\) o\(y=A_0e^{kx}\). Al realizar análisis de regresión, utilizamos la forma más utilizada en utilidades gráficas,\(y=ab^x\). Tómese un momento para reflexionar sobre las características que ya aprendimos sobre la función exponencial\(y=ab^x\) (asuma\(a>0\)):

• \(b\)debe ser mayor que cero y no igual a uno.
• El valor inicial del modelo es\(y=a\).
  • Si\(b>1\), la función modela el crecimiento exponencial. A medida que\(x\) aumenta, las salidas del modelo aumentan lentamente al principio, pero luego aumentan cada vez más rápidamente, sin límite.
  • Si\(0<b<1\), la función modela decaimiento exponencial. A medida que\(x\) aumenta, las salidas para el modelo disminuyen rápidamente al principio y luego se nivelan para volverse asintóticas al eje x. En otras palabras, las salidas nunca llegan a ser iguales o inferiores a cero.

Como parte de los resultados, su calculadora mostrará un número conocido como coeficiente de correlación, etiquetado por la variable\(r\), o\(r^2\). (Es posible que tenga que cambiar la configuración de la calculadora para que se muestren.) Los valores son una indicación de la “bondad de ajuste” de la ecuación de regresión a los datos. Más comúnmente usamos el valor de\(r^2\) en lugar de\(r\), pero cuanto más cerca esté cualquiera de los dos valores\(1\), mejor se aproximará la ecuación de regresión a los datos.

Regresión exponencial

La regresión exponencial se utiliza para modelar situaciones en las que el crecimiento comienza lentamente y luego se acelera rápidamente sin límite, o donde la decadencia comienza rápidamente y luego se ralentiza para acercarse cada vez más a cero. Usamos el comando “ExpreG” en una utilidad gráfica para ajustar una función exponencial a un conjunto de puntos de datos. Esto devuelve una ecuación de la forma,

\[y=ab^x\]

Tenga en cuenta que:

• \(b\)debe ser no negativo.
• cuando\(b>1\), tenemos un modelo de crecimiento exponencial.
• cuando\(0<b<1\), tenemos un modelo de decaimiento exponencial.

Cómo: Dado un conjunto de datos, realizar regresión exponencial usando una utilidad gráfica

1. Utilice el menú STAT y luego EDITAR para ingresar datos dados.
   1. Borre los datos existentes de las listas.
   2. Enumere los valores de entrada en la columna L1.
   3. Enumere los valores de salida en la columna L2.
2. Grafique y observe una gráfica de dispersión de los datos utilizando la función STATPLOT.
   1. Utilice ZOOM [9] para ajustar los ejes para ajustarse a los datos.
   2. Verificar que los datos sigan un patrón exponencial.
3. Encuentra la ecuación que modela los datos.
   1. Seleccione “ExpreG” en el menú STAT y luego CALC.
   2. Utilice los valores devueltos para a y b para registrar el modelo,\(y=ab^x\).
4. Grafique el modelo en la misma ventana que la gráfica de dispersión para verificar que es un buen ajuste para los datos.

Ejemplo\(\PageIndex{1}\): Using Exponential Regression to Fit a Model to Data

En 2007, se publicó un estudio universitario que investigaba el riesgo de accidente de conducir con problemas de alcohol. Los datos de\(2,871\) choques se utilizaron para medir la asociación del nivel de alcohol en la sangre (BAC) de una persona con el riesgo de estar en un accidente. En la tabla se\(\PageIndex{1}\) muestran los resultados del estudio. El riesgo relativo es una medida de cuántas veces más probabilidades tiene una persona de chocar. Entonces, por ejemplo, una persona con un BAC de\(0.09\) es\(3.54\) veces más probable que se estrelle como una persona que no ha estado bebiendo alcohol.

Mesa\(\PageIndex{1}\)

BAC	0	0.01	0.03	0.05	0.07	0.09
Riesgo Relativo de Choque	1	1.03	1.06	1.38	2.09	3.54
BAC	0.11	0.13	0.15	0.17	0.19	0.21
Riesgo Relativo de Choque	6.41	12.6	22.1	39.05	65.32	99.78

1. Dejar\(x\) representar el nivel de BAC, y dejar\(y\) representar el riesgo relativo correspondiente. Utilice la regresión exponencial para ajustar un modelo a estos datos.
2. Después de\(6\) las bebidas, una persona que pesa\(160\) libras tendrá un BAC de aproximadamente\(0.16\). ¿Cuántas veces más probable es que una persona con este peso se estrelle si conduce después de tener un\(6\) paquete de cerveza? Redondear a la centésima más cercana.

Solución

1. Usando el menú STAT y luego EDITAR en una utilidad gráfica, enumere los valores de BAC en L1 y los valores de riesgo relativo en L2. Luego use la función STATPLOT para verificar que la gráfica de dispersión siga el patrón exponencial que se muestra en la Figura\(\PageIndex{1}\):

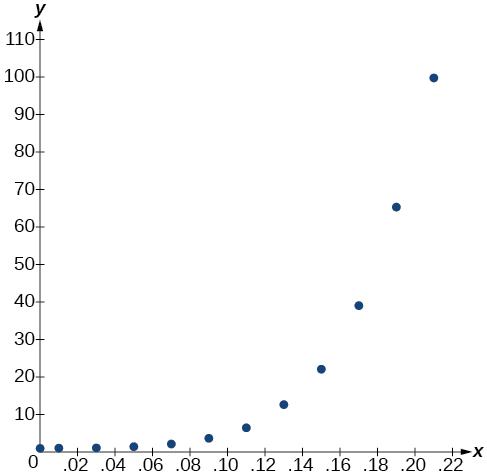
Figura\(\PageIndex{1}\)

Utilice el comando “ExpreG” del menú STAT luego CALC para obtener el modelo exponencial,

\(y=0.58304829{(2.20720213E10)}^x\)

Convirtiendo de notación científica, tenemos:

\(y=0.58304829{(22,072,021,300)}^x\)

Observe\(r^2≈0.97\) que lo que indica que el modelo es un buen ajuste a los datos. Para ver esto, grafica el modelo en la misma ventana que el diagrama de dispersión para verificar que es un buen ajuste como se muestra en la Figura\(\PageIndex{2}\):

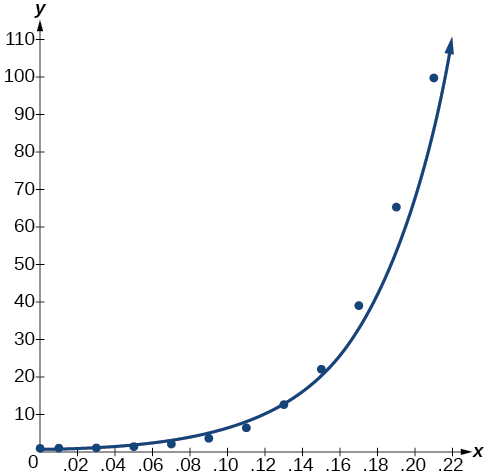
Figura\(\PageIndex{2}\)

2. Utilice el modelo para estimar el riesgo asociado a un BAC de\(0.16\). Sustituir\(0.16\)\(x\) en el modelo y resolver para\(y\).

\[\begin{align*} y&= 0.58304829{(22,072,021,300)}^x \qquad \text{Use the regression model found in part } (a)\\ &= 0.58304829{(22,072,021,300)}^{0.16} \qquad \text{Substitute 0.16 for x}\\ &\approx 26.35 \qquad \text{Round to the nearest hundredth} \end{align*}\]

Si una persona de\(160\) -libra conduce después de\(6\) tomar algo, es aproximadamente\(26.35\) veces más probable que se estrelle que si conduce sobrio.

Ejercicio\(\PageIndex{1}\)

\(\PageIndex{2}\)La tabla muestra el saldo de una tarjeta de crédito de recién egresado cada mes después de graduarse

Mesa\(\PageIndex{2}\)

Mes	1	2	3	4	5	6	7	8
Deuda ($)	620.00	761.88	899.80	1039.93	1270.63	1589.04	1851.31	2154.92

1. Utilice la regresión exponencial para ajustar un modelo a estos datos.
2. Si el gasto continúa a este ritmo, ¿cuál será la deuda de la tarjeta de crédito del egresado al año de graduarse?

Contestar a

El modelo de regresión exponencial que se ajusta a estos datos es\(y=522.88585984{(1.19645256)}^x\).

Respuesta b

Si el gasto continúa a esta tasa, la deuda de la tarjeta de crédito del egresado será\($4,499.38\) después de un año.

Q&A: ¿Es razonable suponer que un modelo de regresión exponencial representará una situación indefinidamente?

No. Recuerde que los modelos están formados por datos del mundo real recopilados para regresión. Por lo general, es razonable hacer estimaciones dentro del intervalo de observación original (interpolación). Sin embargo, cuando se usa un modelo para hacer predicciones, es importante usar habilidades de razonamiento para determinar si el modelo tiene sentido para entradas mucho más allá del intervalo de observación original (extrapolación).

Construyendo un Modelo Logarítmico a partir de Datos

Al igual que con las funciones exponenciales, hay muchas aplicaciones del mundo real para funciones logarítmicas: intensidad del sonido, niveles de pH de soluciones, rendimientos de reacciones químicas, producción de bienes y crecimiento de bebés. Al igual que con los modelos exponenciales, los datos modelados por funciones logarítmicas están siempre aumentando o siempre disminuyendo a medida que el tiempo avanza. Nuevamente, es la forma en que aumentan o disminuyen lo que nos ayuda a determinar si un modelo logarítmico es lo mejor.

Recordemos que las funciones logarítmicas aumentan o disminuyen rápidamente al principio, pero luego se ralentizan constantemente a medida que avanza el tiempo. Al reflexionar sobre las características que ya hemos aprendido sobre esta función, podemos analizar mejor las situaciones del mundo real que reflejan este tipo de crecimiento o decaimiento. Al realizar análisis de regresión logarítmica, utilizamos la forma de la función logarítmica más comúnmente utilizada en utilidades gráficas,\(y=a+b\ln(x)\). Para esta función

• Todos los valores de entrada\(x\),, deben ser mayores que cero.
• El punto\((1,a)\) está en la gráfica del modelo.
• Si\(b>0\), el modelo va en aumento. El crecimiento aumenta rápidamente al principio y luego se ralentiza constantemente con el tiempo.
• Si\(b<0\), el modelo es decreciente. La descomposición ocurre rápidamente al principio y luego se ralentiza constantemente con el tiempo.

Regresión logarít

La regresión logarítmica se utiliza para modelar situaciones en las que el crecimiento o decaimiento se acelera rápidamente al principio y luego se ralentiza Usamos el comando “LNReg” en una utilidad gráfica para ajustar una función logarítmica a un conjunto de puntos de datos. Esto devuelve una ecuación de la forma,

\[y=a+b\ln(x)\]

Tenga en cuenta que

• todos los valores de entrada\(x\),, deben ser no negativos.
• cuando\(b>0\), el modelo va en aumento.
• cuando\(b<0\), el modelo es decreciente.

Cómo: Dado un conjunto de datos, realizar regresión logarítmica usando una utilidad gráfica

1. Utilice el menú STAT y luego EDITAR para ingresar datos dados.
   1. Borre los datos existentes de las listas.
   2. Enumere los valores de entrada en la columna L1.
   3. Enumere los valores de salida en la columna L2.
2. Grafique y observe una gráfica de dispersión de los datos utilizando la función STATPLOT.
   1. Utilice ZOOM [9] para ajustar los ejes para ajustarse a los datos.
   2. Verificar que los datos sigan un patrón logarítmico.
3. Encuentra la ecuación que modela los datos.
   1. Seleccione “LNReg” en el menú STAT y luego CALC.
   2. Utilice los valores devueltos para a y b para registrar el modelo,\(y=a+b\ln(x)\).
4. Grafique el modelo en la misma ventana que la gráfica de dispersión para verificar que es un buen ajuste para los datos.

Ejemplo\(\PageIndex{2}\): Using Logarithmic Regression to Fit a Model to Data

Debido a los avances en la medicina y mayores niveles de vida, la esperanza de vida ha ido en aumento en la mayoría de los países desarrollados desde principios del ^siglo XX. En el cuadro se\(\PageIndex{3}\) muestran las expectativas de vida promedio, en años, de los estadounidenses entre 1900 y 2010.

Mesa \(\PageIndex{3}\)

Año	1900	1910	1920	1930	1940	1950
Esperanza de vida (años)	47.3	50.0	54.1	59.7	62.9	68.2
Año	1960	1970	1980	1990	2000	2010
Esperanza de vida (años)	69.7	70.8	73.7	75.4	76.8	78.7

1. Vamos a\(x\) representar el tiempo en décadas comenzando con\(x=1\) para el año 1900,\(x=2\) para el año 1910, y así sucesivamente. Dejar\(y\) representar la esperanza de vida correspondiente. Utilice regresión logarítmica para ajustar un modelo a estos datos.
2. Utilice el modelo para predecir la esperanza de vida promedio estadounidense para el año 2030.

Solución

1. Usando el menú STAT y luego EDITAR en una utilidad gráfica, enumere los años usando valores\(1–12\) en L1 y la esperanza de vida correspondiente en L2. Luego use la función STATPLOT para verificar que la gráfica de dispersión siga un patrón logarítmico como se muestra en la Figura\(\PageIndex{3}\):

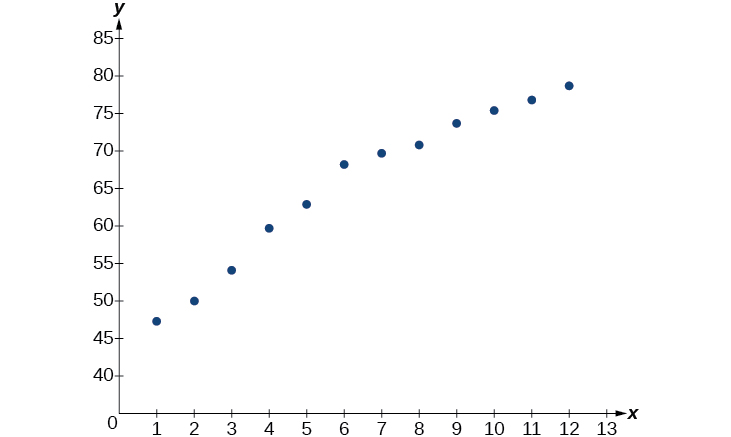
Figura\(\PageIndex{3}\)

Utilice el comando “LNReg” del menú STAT luego CALC para obtener el modelo logarítmico,

\(y=42.52722583+13.85752327\ln(x)\)

A continuación, grafica el modelo en la misma ventana que la gráfica de dispersión para verificar que es un buen ajuste como se muestra en la Figura\(\PageIndex{4}\):

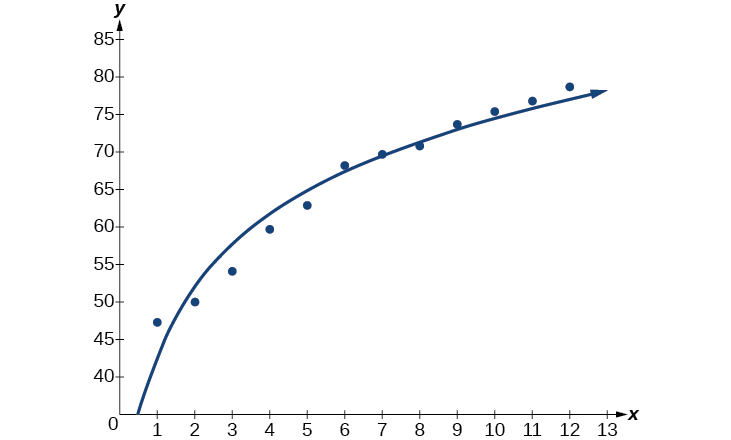
Figura\(\PageIndex{4}\)

2. Para predecir la esperanza de vida de un estadounidense en el año\(2030\), sustituir\(x=14\) a la en el modelo y resolver por\(y\):

\[\begin{align*} y&= 42.52722583+13.85752327\ln(x) \qquad \text{Use the regression model found in part } (a)\\ &= 42.52722583+13.85752327\ln(14) \qquad \text{Substitute 14 for x}\\ &\approx 79.1 \qquad \text{Round to the nearest tenth} \end{align*}\]

Si la esperanza de vida sigue aumentando a este ritmo, la esperanza de vida promedio de un estadounidense será\(79.1\) por año\(2030\).

Ejercicio\(\PageIndex{2}\)

Las ventas de un videojuego lanzado en el año 2000 despegaron al principio, pero luego se ralentizaron de manera constante a medida que avanzaba el tiempo. En la tabla se\(\PageIndex{4}\) muestra el número de juegos vendidos, en miles, de los años 2000—2010.

Mesa\(\PageIndex{4}\)

Año	2000	2001	2002	2003	2004	2005
Número Vendido (miles)	142	149	154	155	159	161
Año	2006	2007	2008	2009	2010	-
Número Vendido (miles)	163	164	164	166	167	-

Vamos a\(x\) representar el tiempo en años a\(x=1\) partir del año 2000. Vamos a\(y\) representar el número de juegos vendidos en miles.

1. Utilice regresión logarítmica para ajustar un modelo a estos datos.
2. Si los juegos siguen vendiéndose a este ritmo, ¿cuántos juegos se venderán en 2015? Redondear al mil más cercano.

Contestar a

El modelo de regresión logarítmica que se ajusta a estos datos es\(y=141.91242949+10.45366573\ln(x)\)

Respuesta b

Si las ventas continúan a este ritmo, sobre\(171,000\) los juegos se venderán en el año\(2015\).

Construyendo un Modelo Logístico a partir de Datos

Al igual que el crecimiento exponencial y logarítmico, el crecimiento logístico aumenta con el tiempo. Una de las diferencias más notables con los modelos de crecimiento logístico es que, en cierto punto, el crecimiento se ralentiza constantemente y la función se acerca a un límite superior, o valor limitante. Debido a esto, la regresión logística es la mejor para modelar fenómenos donde hay límites en la expansión, como la disponibilidad de espacio vital o nutrientes.

Cabe señalar que las funciones logísticas en realidad modelan el crecimiento exponencial limitado en recursos. Hay muchos ejemplos de este tipo de crecimiento en situaciones del mundo real, entre ellos el crecimiento poblacional y la propagación de enfermedades, rumores, e incluso manchas en la tela. Al realizar análisis de regresión logística, utilizamos la forma más utilizada en las utilidades gráficas:

\(y=\dfrac{c}{1+ae^{−bx}}\)

Recordemos que:

• \(\dfrac{c}{1+a}\)es el valor inicial del modelo.
• cuando\(b>0\), el modelo aumenta rápidamente al principio hasta alcanzar su punto de tasa máxima de crecimiento,\((\dfrac{\ln(a)}{b}, \dfrac{c}{2})\). En ese punto, el crecimiento se ralentiza constantemente y la función se vuelve asintótica al límite superior\(y=c\).
• \(c\)es el valor limitante, a veces llamado capacidad de carga, del modelo.

Regresión logística

La regresión logística se utiliza para modelar situaciones donde el crecimiento se acelera rápidamente al principio y luego se ralentiza constantemente hasta un límite superior. Utilizamos el comando “Logistic” en una utilidad gráfica para ajustar una función logística a un conjunto de puntos de datos. Esto devuelve una ecuación de la forma

\[y=\dfrac{c}{1+ae^{−bx}}\]

Tenga en cuenta que

• El valor inicial del modelo es\(\dfrac{c}{1+a}\).
• Los valores de salida para el modelo se acercan cada vez más a\(y=c\) medida que aumenta el tiempo.

Cómo: Dado un conjunto de datos, realizar regresión logística usando una utilidad gráfica

1. Utilice el menú STAT y luego EDITAR para ingresar datos dados.
   1. Borre los datos existentes de las listas.
   2. Enumere los valores de entrada en la columna L1.
   3. Enumere los valores de salida en la columna L2.
2. Grafique y observe una gráfica de dispersión de los datos utilizando la función STATPLOT.
   1. Utilice ZOOM [9] para ajustar los ejes para ajustarse a los datos.
   2. Verificar que los datos sigan un patrón logístico.
3. Encuentra la ecuación que modela los datos.
   1. Seleccione “Logística” en el menú STAT y luego CALC.
   2. Utilice los valores devueltos para\(a\)\(b\),, y\(c\) para registrar el modelo,\(y=\dfrac{c}{1+ae^{−bx}}\).
4. Grafique el modelo en la misma ventana que la gráfica de dispersión para verificar que es un buen ajuste para los datos.

Ejemplo\(\PageIndex{3}\): Using Logistic Regression to Fit a Model to Data

El servicio de telefonía móvil ha aumentado rápidamente en Estados Unidos desde mediados de la década de 1990. Hoy en día, casi todos los residentes cuentan con servicio celular. En la tabla se\(\PageIndex{5}\) muestra el porcentaje de estadounidenses con servicio celular entre los años 1995 y 2012.

Mesa\(\PageIndex{5}\)

Año	Americanos con servicio celular (%)	Año	Americanos con servicio celular (%)
1995	12.69	2004	62.852
1996	16.35	2005	68.63
1997	20.29	2006	76.64
1998	25.08	2007	82.47
1999	30.81	2008	85.68
2000	38.75	2009	89.14
2001	45.00	2010	91.86
2002	49.16	2011	95.28
2003	55.15	2012	98.17

1. Vamos a\(x\) representar el tiempo en años a\(x=0\) partir del año 1995. Dejar\(y\) representar el porcentaje correspondiente de residentes con servicio celular. Utilice la regresión logística para ajustar un modelo a estos datos.
2. Utilice el modelo para calcular el porcentaje de estadounidenses con servicio celular en el año 2013. Redondear a la décima más cercana de un porcentaje.
3. Discutir el valor devuelto para el límite superior,\(c\). ¿Qué te dice esto sobre el modelo? ¿Cuál sería el valor límite si el modelo fuera exacto?

Solución

1. Usando el menú STAT y luego EDITAR en una utilidad gráfica, enumere los años usando valores\(0–15\) en L1 y el porcentaje correspondiente en L2. Luego use la función STATPLOT para verificar que la gráfica de dispersión siga un patrón logístico como se muestra en la Figura\(\PageIndex{5}\):

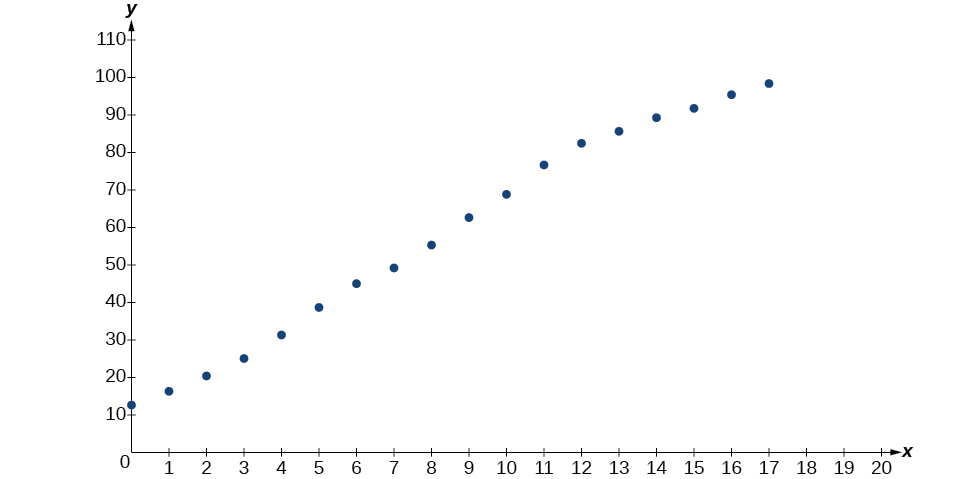
Figura\(\PageIndex{5}\)

Utilice el comando “Logistic” del menú STAT luego CALC para obtener el modelo logístico,

\[y=105.73795261+6.88328979e^{−0.2595440013x}\]

A continuación, grafica el modelo en la misma ventana como se muestra en\(\PageIndex{6}\) la Figura la gráfica de dispersión para verificar que es un buen ajuste:

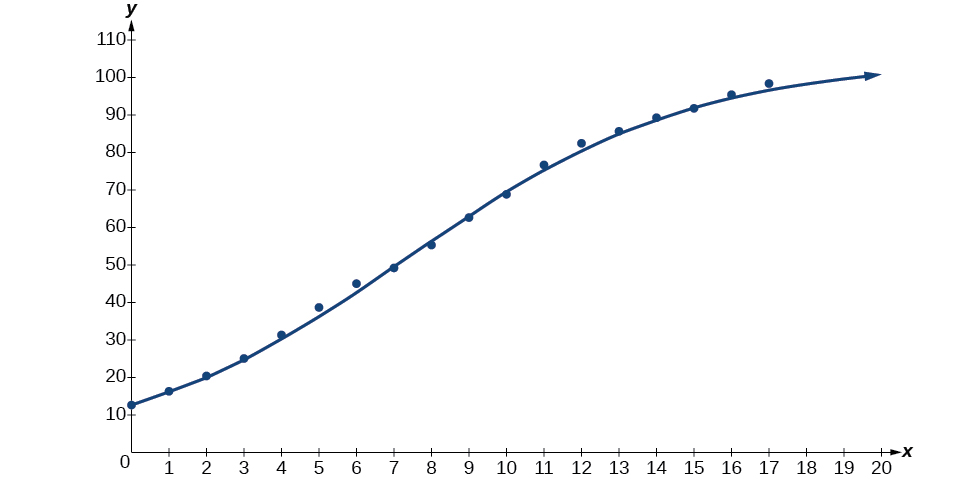
Figura\(\PageIndex{6}\)

2. Para aproximar el porcentaje de estadounidenses con servicio celular en el año 2013, sustituir\(x=18\) al en el modelo y resolver por\(y\):

\[\begin{align*} y&= \dfrac{105.7379526}{1+6.88328979e^{-0.2595440013x}} \qquad \text{Use the regression model found in part } (a)\\ &= \dfrac{105.7379526}{1+6.88328979e^{-0.2595440013(18)}} \qquad \text{Substitute 18 for x}\\ &\approx 99.3 \qquad \text{Round to the nearest tenth} \end{align*}\]

Según el modelo, alrededor del 98.8% de los estadounidenses tenían servicio celular en 2013.

3. El modelo da un valor limitante de aproximadamente\(105\). Esto quiere decir que el porcentaje máximo posible de estadounidenses con servicio celular sería\(105%\), lo cual es imposible. (¿Cómo podría más\(100%\) de una población tener servicio celular?) Si el modelo fuera exacto, el valor límite sería\(c=100\) y las salidas del modelo se acercarían mucho, pero nunca llegarían realmente\(100%\). Después de todo, ¡siempre habrá alguien ahí fuera sin servicio celular!

Ejercicio\(\PageIndex{3}\)

El cuadro\(\PageIndex{6}\) muestra la población, en miles, de focas portuarias en el Mar de Wadden durante los años 1997 a 2012.

Mesa\(\PageIndex{6}\)

Año	Población de focas (miles)	Año	Población de focas (miles)
1997	3.493	2005	19.590
1998	5.282	2006	21.955
1999	6.357	2007	22.862
2000	9.201	2008	23.869
2001	11.224	2009	24.243
2002	12.964	2010	24.344
2003	16.226	2011	24.919
2004	18.137	2012	25.108

Vamos a\(x\) representar el tiempo en años a\(x=0\) partir del año 1997. Vamos a\(y\) representar el número de sellos en miles.

1. Utilice la regresión logística para ajustar un modelo a estos datos.
2. Utilizar el modelo para predecir la población de focas para el año 2020.
3. Al número entero más cercano, ¿cuál es el valor limitante de este modelo?

Contestar a

El modelo de regresión logística que se ajusta a estos datos es\(y=\dfrac{25.65665979}{1+6.113686306e^{−0.3852149008x}}\).

Respuesta b

Si la población sigue creciendo a este ritmo, habrá alrededor de\(25,634\) sellos en 2020.

Respuesta c

Al número entero más cercano, la capacidad de carga es\(25,657\).

Medios

Acceda a este recurso en línea para obtener instrucción y práctica adicionales con modelos de funciones exponenciales.

• Regresión exponencial en una calculadora

Visite este sitio web para obtener preguntas de práctica adicionales de Learningpod.

Conceptos clave

• La regresión exponencial se utiliza para modelar situaciones donde el crecimiento comienza lentamente y luego se acelera rápidamente sin límite, o donde la decadencia comienza rápidamente y luego se ralentiza para acercarse cada vez más a cero.
• Utilizamos el comando “ExpreG” en una utilidad gráfica para ajustar la función del formulario\(y=ab^x\) a un conjunto de puntos de datos. Ver Ejemplo\(\PageIndex{1}\).
• La regresión logarítmica se utiliza para modelar situaciones en las que el crecimiento o decaimiento se acelera rápidamente al principio y luego se ralentiza
• Usamos el comando “LNReg” en una utilidad gráfica para ajustar una función del formulario\(y=a+b\ln(x)\) a un conjunto de puntos de datos. Ver Ejemplo\(\PageIndex{2}\).
• La regresión logística se utiliza para modelar situaciones donde el crecimiento se acelera rápidamente al principio y luego se ralentiza constantemente a medida que la función se acerca a un límite superior.
• Utilizamos el comando “Logistic” en una utilidad gráfica para ajustar una función del formulario\(y=\dfrac{c}{1+ae^{−bx}}\) a un conjunto de puntos de datos. Ver Ejemplo\(\PageIndex{3}\).

Colaboradores y Atribuciones

• Template:ContribOpenStaxPreCalc