19.5: Ejercicios

Última actualización
Guardar como PDF

Page ID: 111277

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

1

Dibuje el diagrama de celosía para el conjunto de potencia de$X = \{ a, b, c, d \}$ con la relación de inclusión del conjunto,$\subset\text{.}$

2

Dibuja el diagrama para el conjunto de enteros positivos que son divisores de ¿$30\text{.}$Es este poset un álgebra booleana?

3

Dibuja un diagrama de la celosía de subgrupos de${\mathbb Z}_{12}\text{.}$

4

Dejar$B$ ser el conjunto de enteros positivos que son divisores de$210\text{.}$ Definir un orden on$B$ por$a \preceq b$ si$a \mid b\text{.}$ Prove que$B$ es un álgebra booleana. Encuentra un conjunto$X$ tal que$B$ sea isomórfico para${\mathcal P}(X)\text{.}$

5

Demostrar o desmentir:${\mathbb Z}$ es un poset bajo la relación$a \preceq b$ si$a \mid b\text{.}$

6

Dibuje el circuito de conmutación para cada una de las siguientes expresiones booleanas.

$\displaystyle (a \vee b \vee a') \wedge a$
$\displaystyle (a \vee b)' \wedge (a \vee b)$
$\displaystyle a \vee (a \wedge b)$
$\displaystyle (c \vee a \vee b) \wedge c' \wedge (a \vee b)'$

7

Dibuja un circuito que se cerrará exactamente cuando solo uno de los tres interruptores$a\text{,}$$b\text{,}$ y$c$ estén cerrados.

8

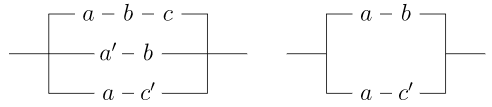
Demostrar o desacreditar que los dos circuitos mostrados son equivalentes.

$clipboard_e5662dbc2f7ce018ed67a8d7fd8774ac7.png$

9

Let$X$ Ser un conjunto finito que contiene$n$ elementos. Demostrar que$|{\cal P}(X)| = 2^n\text{.}$ Concluir que el orden de cualquier álgebra booleana finita debe ser$2^n$ para algunos$n \in {\mathbb N}\text{.}$

10

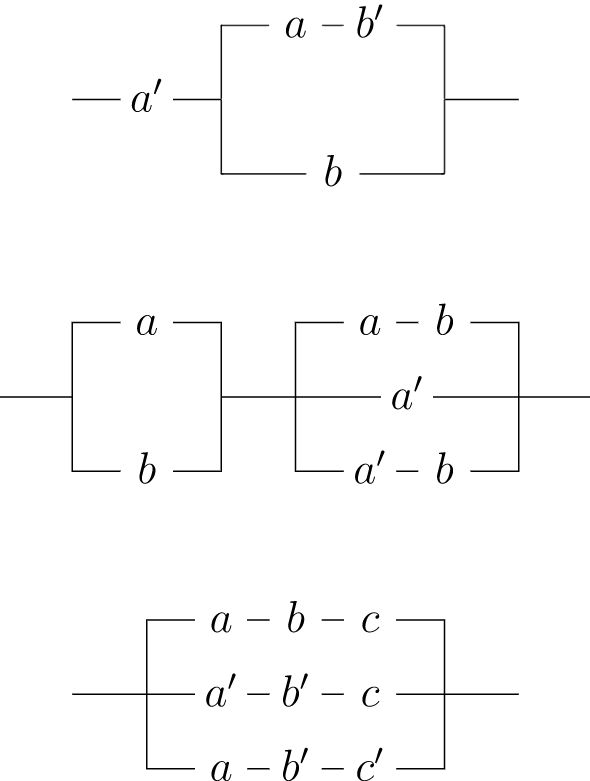
Para cada uno de los siguientes circuitos, escriba una expresión booleana. Si el circuito puede ser reemplazado por uno con menos interruptores, dé la expresión booleana y dibuje un diagrama para el nuevo circuito.

$clipboard_e71296a28342c24abfd0d3d8babc75aa2.png$

11

Demostrar o desacreditar: El conjunto de todos los enteros distintos de cero es una celosía, donde$a \preceq b$ se define por$a \mid b\text{.}$

12

$L$Sea un conjunto no vacío con dos operaciones binarias$\vee$ y que$\wedge$ satisfaga las leyes conmutativa, asociativa, idempotente y de absorción. Podemos definir un orden parcial sobre$L\text{,}$ como en Teorema$19.14$, por$a \preceq b$ si$a \vee b = b\text{.}$ Demostrar que el mayor límite inferior de$a$ y$b$ es$a \wedge b\text{.}$

13

Dejar$G$ ser un grupo y$X$ ser el conjunto de subgrupos de$G$ ordenado por inclusión set-teórica. Si$H$ y$K$ son subgrupos de$G\text{,}$ mostrar que el límite inferior superior de$H$ y$K$ es el subgrupo generado por$H \cup K\text{.}$

14

Que$R$ sea un anillo y supongamos que$X$ es el conjunto de ideales de$R\text{.}$ Show que$X$ es un poset ordenado por la inclusión teórica del conjunto,$\subset\text{.}$ Definir el encuentro de dos ideales$I$ y$J$ en$X$ por$I \cap J$ y la unión de$I$ y$J$ por $I + J\text{.}$Demostrar que el conjunto de ideales de$R$ es una celosía bajo estas operaciones.

15

$B$Sea un álgebra booleana. Demostrar cada una de las siguientes identidades.

$a \vee I = I$y$a \wedge O = O$ para todos$a \in B\text{.}$
Si$a \vee b = I$ y$a \wedge b = O\text{,}$ entonces$b = a'\text{.}$
$(a')'=a$para todos$a \in B\text{.}$
$I' = O$y$O' = I\text{.}$
$(a \vee b)' = a' \wedge b'$y$(a \wedge b)' = a' \vee b'$ (Leyes de De Morgan).

16

Al dibujar los diagramas apropiados, complete la prueba del Teorema$19.30$ para mostrar que las funciones de conmutación forman un álgebra booleana.

17

$B$Sea un álgebra booleana. Definir operaciones binarias$+$ y$\cdot$ encendido$B$ por

\ begin {alinear*} a + b & = (a\ cuña b')\ vee (a'\ cuña b)\\ a\ cdot b & = a\ cuña b\ texto {.} \ end {align*}

Demostrar que$B$ es un anillo conmutativo bajo estas operaciones satisfaciendo$a^2 = a$ para todos$a \in B\text{.}$

18

Que$X$ sea un poset tal que para cada$a$ y$b$ en$X\text{,}$ cualquiera$a \preceq b$ o$b \preceq a\text{.}$ Entonces$X$ se dice que es un conjunto totalmente ordenado.

Es$a \mid b$ un pedido total en${\mathbb N}\text{?}$
Demostrar que${\mathbb N}\text{,}$${\mathbb Z}\text{,}$${\mathbb Q}\text{,}$ y${\mathbb R}$ son conjuntos totalmente ordenados bajo el pedido habitual$\leq\text{.}$

19

Dejar$X$ y$Y$ ser posets. Un mapa$\phi : X \rightarrow Y$ es conservadora de orden si$a \preceq b$ implica que$\phi(a) \preceq \phi(b)\text{.}$ Let$L$ and$M$ be celosías. Un mapa$\psi: L \rightarrow M$ es un homomorfismo de celosía si$\psi( a \vee b ) = \psi(a) \vee \psi(b)$ y$\psi( a \wedge b ) = \psi(a) \wedge \psi(b)\text{.}$ Mostrar que cada homomorfismo de celosía es conservadora de orden, pero que no es el caso de que todo homomorfismo conservador de orden sea un homomorfismo de celosía.

20

$B$Sea un álgebra booleana. Demostrar que$a = b$ si y sólo si$(a \wedge b') \vee ( a' \wedge b) = O$ por$a, b \in B\text{.}$

21

$B$Sea un álgebra booleana. Demostrar que$a = O$ si y solo si$(a \wedge b') \vee ( a' \wedge b) = b$ por todos$b \in B\text{.}$

22

Dejar$L$ y$M$ ser celosías. Definir una relación de orden on$L \times M$ by$( a, b) \preceq (c, d)$ if$a \preceq c$ y$b \preceq d\text{.}$ Mostrar que$L \times M$ es una celosía bajo este orden parcial.