6.1: Acciones grupales

Última actualización
Guardar como PDF

Page ID: 111024

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las acciones grupales nos devuelven a nuestra visión original de los grupos como medidas de simetría. Comenzamos con una definición.

Definición 6.0.1

Let$G$ be a group. A set $S$ is a (left) $G$-set if there is a function from $G\times S\rightarrow S$ (which we will write as $g\cdot s$ for $g\in G, s\in S$) satisfying:

$(gh)\cdot s = g\cdot (h\cdot s)$ for all $g, h\in G, s\in S$, and
$1\cdot s=s$ for all $s\in S$.

Se puede escribir una definición análoga para un derecho$G$-set; a right $G$-set has a function from $S\times G\rightarrow S$.

Estas condiciones dicen, en lenguaje sencillo, que los elementos de$G$ move objects in the set to other objects, in a way which respects the group operation. (ie, it doesn't matter whether you perform the operation before or after applying the action.) Furthermore, the identity fixes every element of the set.

Lo mejor es comenzar con algunos ejemplos combinatorios fáciles.

Let$G$ be a group and $S$ be any set. The trivial action of $G$ on $S$ is given by $g\cdot s=s$ for every $g\in G, s\in S$. One can easily check that the conditions for a group action hold!
Considerar$S_n$ and a set $S$ of $n$ labelled objects. Then the permutations of the objects constitute an action of $S_n$ on $S$.
Pero$S_n$ can also act on sets with more than $n$ elements! Consider a regular deck of playing cards; each card has one of four suits (Clubs, Spades, Hearts, or Diamonds) and are numbered $1$ to $13$. (Where a Jack is $11$, Queen is $12$ and King is $13$.) We can write each card in a short form: $4D$ is short for 'four of diamonds.' Then $S_4$ acts on the deck of cards by permuting the suits of the cards. For example, consider the permutation $\sigma$ which transposes hearts and diamonds while leaving clubs and spades alone. Then $\sigma(4D)=4H$, and $\sigma(12C)=12C$.
Por otra parte,$S_{13}$ acts on the values of the cards while leaving the suits alone. For convenience, we write the action on values of cards on the right and the action on suits on the left. Let $\tau$ be the permutation in $S_{13}$ which sends $i$ to $i+1$, and $13$ to $1$. Then $4D\cdot \tau=5D$. Combining the left and right actions, we have $\sigma\cdot 4D\cdot \tau=5H$, for example.
Y$S_n$ can act on sets with fewer than $n$ elements. Consider a coin, with a 'heads' side ($H$) and a 'tails' side ($T$). We can define an action of $S_n$ where $\sigma$ flips the coin if the sign of $\sigma$ is negative, and leaves the coin alone if the sign of $\sigma$ is positive. Here the set we're acting on is actually the set of states of the coin: $\{H, T\}$.

Así como hicimos gráficas Cayley de grupos, también podemos hacer gráficas Cayley de acciones grupales. Si nuestro grupo$G$ has a generating set $\{g_1, g_2, \ldots, g_k\}$, then the Cayley graph has one vertex for each element of the set $S$ and colored edges from each $s$ to $g_i\cdot s$.

Para el ejemplo de$S_n$ acting on a coin, the Cayley graph will just have two vertices, $H$ and $T$, and arrows according to the action of the generators. If we consider the generating set of simple transpositions (which, we'll recall, exchange $i$ and $i+1$ and leave everything else alone), the Cayley graph will have arrows from $H$ to $T$ and back for each simple transposition. (Because all simple transpositions have sign $-1$.)

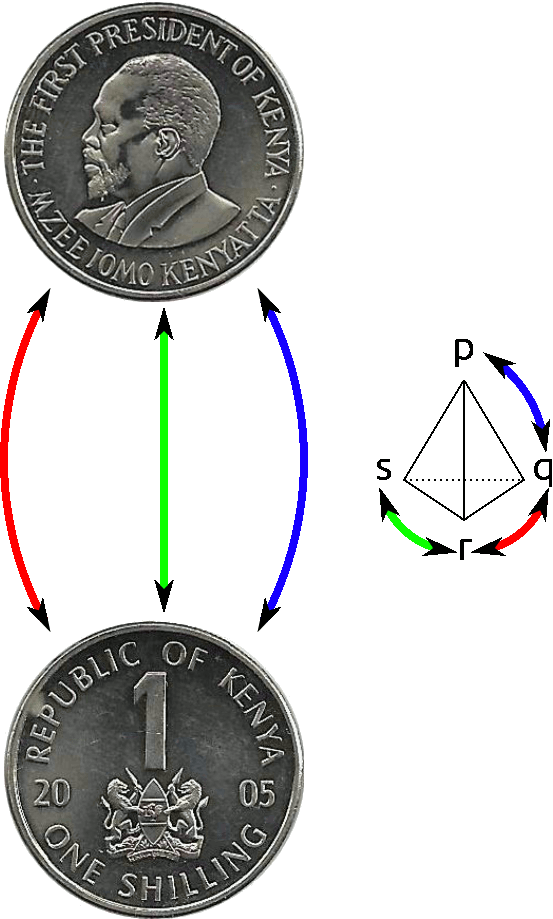
$s4coinAction.gif$

Figura 6.1: Gráfica de Cayley para la acción de$S_4$ on a coin, with generators given by the simple transpositions.

$S_n$ has another generating set consisting of the transposition $[2,1,3,4,\ldots,n]$ and the rotation $[n,1,2,\ldots,n-1]$. Draw the Cayley graph of $S_n$ acting on the coin with these generators. (Note that the Cayley graph may be different for different $n$.)

Let's build a Cayley graph for the cards, but with a smaller set of cards to make things easier to draw. Imagine our deck only has two suits - Spades and Diamonds - and only numbers $1$ through $4$. Then let $S_4$ act on the left by permuting numbers. The Cayley graph is below.

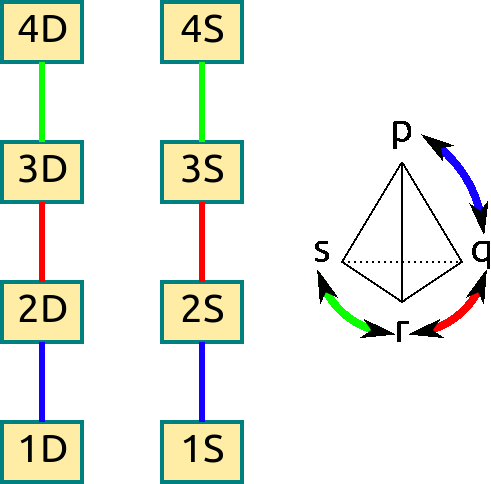
$s4CardAction.gif$

Figura 6.2: Diagrama de Cayley para$S_4$ acting on some cards numbered $1$ through $4$, whose suits are all either diamonds (D) or spades (S).

Observe que la acción se divide en dos piezas conectadas diferentes: El intercambio de números nunca nos permitirá cambiar de trajes, pero podemos cambiar los números libremente. En consecuencia, cada uno de los trajes forma un 'bloque' desde el que no se puede llegar a los otros bloques. Estos bloques se llaman órbitas; los estudiaremos intensamente en la siguiente sección.

Colaboradores y Atribuciones

Template:ContribDenton

Search

\(S_n\) has another generating set consisting of the transposition \([2,1,3,4,\ldots,n]\) and the rotation \([n,1,2,\ldots,n-1]\). Draw the Cayley graph of \(S_n\) acting on the coin with these generators. (Note that the Cayley graph may be different for different \(n\).)