1.4: Existencia y singularidad de las soluciones
- Page ID
- 116466
- T/F: Es posible que un sistema lineal tenga exactamente 5 soluciones.
- T/F: Una variable que corresponde a un 1 inicial es “libre”.
- ¿Cómo se puede saber qué tipo de solución tiene un sistema lineal de ecuaciones?
- Dar un ejemplo (diferente a los dados en el texto) de una ecuación 2, 2 sistema lineal desconocido que no es consistente.
- T/F: Una solución particular para un sistema lineal con infinitas soluciones se puede encontrar mediante la selección arbitraria de valores para las variables libres.
Hasta el momento, siempre que hemos resuelto un sistema de ecuaciones lineales, siempre hemos encontrado exactamente una solución. No siempre es así; encontraremos en esta sección que algunos sistemas no tienen solución, y otros tienen más de uno.
Empezamos con un ejemplo muy sencillo. Considera el siguiente sistema lineal: Obviamente\[x-y=0. \nonumber \] hay infinitas soluciones a este sistema; siempre y cuando\(x=y\), tengamos una solución. Podemos imaginar todas estas soluciones pensando en la gráfica de la ecuación\(y=x\) en el plano de\(x,y\) coordenadas tradicional.
Continuemos con este aspecto visual de considerar soluciones a sistemas lineales. Considerar el sistema\[\begin{align}\begin{aligned} x+y&=2\\ x-y&=0. \end{aligned}\end{align} \nonumber \] Cada una de estas ecuaciones puede verse como líneas en el plano de coordenadas, y como sus pendientes son diferentes, sabemos que se cruzarán en alguna parte (ver Figura\(\PageIndex{1}\) (a)). En este ejemplo, se cruzan en el punto\((1,1)\) —es decir, cuándo\(x=1\) y\(y=1\), ambas ecuaciones están satisfechas y tenemos una solución a nuestro sistema lineal. Dado que este es el único lugar donde se cruzan las dos líneas, esta es la única solución.
Ahora considere el sistema lineal\[\begin{align}\begin{aligned} x+y&=1\\2x+2y&=2.\end{aligned}\end{align} \nonumber \] Es claro que si bien tenemos dos ecuaciones, son esencialmente la misma ecuación; la segunda es sólo un múltiplo de la primera. Por lo tanto, cuando graficamos las dos ecuaciones, estamos graficando la misma línea dos veces (ver Figura\(\PageIndex{1}\) (b); la línea más gruesa se usa para representar dibujar la línea dos veces). En este caso, tenemos un conjunto de soluciones infinitas, igual que si solo tuviéramos la única ecuación\(x+y=1\). A menudo escribimos la solución como\(x=1-y\) para demostrar que\(y\) puede ser cualquier número real, y\(x\) se determina una vez que elegimos un valor para\(y\).
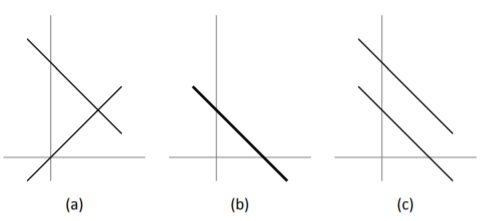
Figura\(\PageIndex{1}\): Las tres posibilidades para dos ecuaciones lineales con dos incógnitas.
Por último, considere el sistema lineal\[\begin{align}\begin{aligned} x+y&=1\\x+y&=2.\end{aligned}\end{align} \nonumber \] Debemos de inmediato detectar un problema con este sistema; si la suma de\(x\) y\(y\) es 1, ¿cómo puede ser también 2? No hay solución a tal problema; este sistema lineal no tiene solución. Podemos visualizar esta situación en la Figura\(\PageIndex{1}\) (c); las dos líneas son paralelas y nunca se cruzan.
Si tuviéramos que considerar un sistema lineal con tres ecuaciones y dos incógnitas, podríamos visualizar la solución graficando las tres líneas correspondientes. Podemos imaginar que tal vez las tres líneas se encontrarían en un punto, dando exactamente 1 solución; quizás las tres ecuaciones describen la misma línea, dando un número infinito de soluciones; quizás tenemos líneas diferentes, pero no todas se encuentran en un mismo punto, sin dar solución alguna. Además, visualizamos situaciones similares con, digamos, 20 ecuaciones con dos variables.
Si bien se vuelve más difícil de visualizar cuando agregamos variables, no importa cuántas ecuaciones y variables tengamos, las soluciones a las ecuaciones lineales siempre vienen en una de tres formas: exactamente una solución, soluciones infinitas, o ninguna solución. Este es un hecho que no vamos a probar aquí, pero merece ser declarado.
Formas de solución de sistemas lineales
Cada sistema lineal de ecuaciones tiene exactamente una solución, soluciones infinitas o ninguna solución.
Esto nos lleva a una definición. Aquí no diferenciamos entre tener una solución e infinitas soluciones, sino simplemente si existe o no una solución.
Un sistema de ecuaciones lineales es consistente si tiene una solución (quizás más de una). Un sistema lineal es inconsistente si no tiene solución.
¿Cómo podemos saber qué tipo de solución (si existe) tiene un sistema dado de ecuaciones lineales? La respuesta a esta pregunta radica en comprender adecuadamente la forma de escalón de fila reducida de una matriz. Para descubrir cuál es la solución a un sistema lineal, primero colocamos la matriz en forma de escalón de fila reducida y luego interpretamos esa forma correctamente.
Antes de comenzar con un ejemplo simple, hagamos una nota sobre cómo encontrar la forma de escalón de fila reducida de una matriz.
En la sección anterior, aprendimos a encontrar la forma de escalón de fila reducida de una matriz usando la eliminación gaussiana — a mano. Necesitamos saber cómo hacer esto; entender el proceso tiene beneficios. Sin embargo, en realidad ejecutar el proceso a mano para cada problema no suele ser beneficioso. De hecho, con sistemas grandes, calcular la forma de escalón de fila reducida a mano es efectivamente imposible. Nuestra principal preocupación es qué es “la rref”, no qué pasos exactos se utilizaron para llegar allí. Por lo tanto, se alienta al lector a emplear alguna forma de tecnología para encontrar la forma de escalón de fila reducida. Se pueden usar programas informáticos como Mathematica, MATLAB, Maple y Derive; muchas calculadoras portátiles (como las calculadoras de Texas Instruments) realizarán estos cálculos muy rápidamente.
Como regla general, cuando estamos aprendiendo una nueva técnica, lo mejor es no usar la tecnología para ayudarnos. Esto nos ayuda a aprender no solo la técnica sino algunos de sus “funcionamientos internos”. Entonces podremos usar la tecnología una vez que hayamos dominado la técnica y ahora estemos aprendiendo a usarla para resolver problemas.
De aquí en adelante, en nuestros ejemplos, cuando necesitamos la forma de escalón de fila reducida de una matriz, no vamos a mostrar los pasos involucrados. Más bien, daremos la matriz inicial, luego inmediatamente daremos la forma de escalón de fila reducida de la matriz. Confiamos en que el lector pueda verificar la exactitud de este formulario realizando los pasos necesarios a mano o utilizando alguna tecnología para hacerlo por ellos.
Nuestro primer ejemplo explora oficialmente un ejemplo rápido utilizado en la introducción de esta sección.
Encuentre la solución al sistema lineal
\[\begin{array}{ccccc} x_1 & +& x_2 & = & 1\\ 2x_1 & + & 2x_2 & = &2\end{array} . \nonumber \]
Solución
Cree la matriz aumentada correspondiente, y luego ponga la matriz en forma de escalón de fila reducida.
\[\left[\begin{array}{ccc}{1}&{1}&{1}\\{2}&{2}&{2}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{ccc}{1}&{1}&{1}\\{0}&{0}&{0}\end{array}\right] \nonumber \]
Ahora vuelve a convertir la matriz reducida en ecuaciones. En este caso, sólo tenemos una ecuación,\[x_1+x_2=1 \nonumber \] o, de manera equivalente,\[\begin{align}\begin{aligned} x_1 &=1-x_2\\ x_2&\text{ is free}. \end{aligned}\end{align} \nonumber \]
Acabamos de introducir un nuevo término, la palabra libre. Se utiliza para enfatizar esa idea que\(x_2\) puede tomar cualquier valor; somos “libres” de elegir cualquier valor para\(x_2\). Una vez elegido este valor,\(x_1\) se determina el valor de. Tenemos infinitas opciones por el valor de\(x_2\), así que por lo tanto tenemos infinitas soluciones.
Por ejemplo, si establecemos\(x_2 = 0\), entonces\(x_1 = 1\); si establecemos\(x_2 = 5\), entonces\(x_1 = -4\).
Probemos otro ejemplo, uno que usa más variables.
Encuentre la solución al sistema lineal\[\begin{array}{ccccccc} & &x_2&-&x_3&=&3\\ x_1& & &+&2x_3&=&2\\ &&-3x_2&+&3x_3&=&-9\\ \end{array}. \nonumber \]
Solución
Para encontrar la solución, ponga la matriz correspondiente en forma de escalón de fila reducida.
\[\left[\begin{array}{cccc}{0}&{1}&{-1}&{3}\\{1}&{0}&{2}&{2}\\{0}&{-3}&{3}&{-9}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{cccc}{1}&{0}&{2}&{2}\\{0}&{1}&{-1}&{3}\\{0}&{0}&{0}&{0}\end{array}\right] \nonumber \]
Ahora convierte esta matriz reducida de nuevo en ecuaciones. Tenemos\[\begin{align}\begin{aligned} x_1 + 2x_3 &= 2 \\ x_2-x_3&=3 \end{aligned}\end{align} \nonumber \] o, equivalentemente,\[\begin{align}\begin{aligned} x_1 &= 2-2x_3 \\ x_2&=3+x_3\\x_3&\text{ is free.} \end{aligned}\end{align} \nonumber \]
Estas dos ecuaciones nos dicen que los valores de\(x_1\) y\(x_2\) dependen de lo que\(x_3\) es. Como vimos antes, no hay restricción sobre lo que\(x_3\) debe ser; es “libre” asumir el valor de cualquier número real. Una vez\(x_3\) elegido, tenemos una solución. Como tenemos infinitas opciones por el valor de\(x_3\), tenemos infinitas soluciones.
Como ejemplos,\(x_1 = 2\),\(x_2 = 3\),\(x_3 = 0\) es una solución;\(x_1 = -2\),\(x_2 = 5\),\(x_3 = 2\) es otra solución. Intente volver a conectar estos valores a las ecuaciones originales para verificar que efectivamente estas son soluciones. (Por cierto, dado que existen infinitas soluciones, este sistema de ecuaciones es consistente.)
En los dos ejemplos anteriores hemos utilizado la palabra “libre” para describir ciertas variables. ¿Qué es exactamente una variable libre? ¿Cómo reconocemos qué variables son libres y cuáles no?
Mira hacia atrás a la matriz reducida en Ejemplo\(\PageIndex{1}\). Observe que solo hay un 1 principal en esa matriz, y que el 1 inicial correspondía a la\(x_1\) variable. Eso nos dijo que no\(x_1\) era una variable libre; ya que\(x_2\) no correspondía a un 1 inicial, era una variable libre.
Mira también la matriz reducida en Ejemplo\(\PageIndex{2}\). Había dos primeros 1s en esa matriz; uno correspondía\(x_1\) y el otro a\(x_2\). Esto significó que\(x_1\) y no\(x_2\) eran variables libres; como no había un 1 principal que correspondiera a\(x_3\), era una variable libre.
Definimos formalmente este y algunos otros términos en esta siguiente definición.
Considere la forma de escalón de fila reducida de una matriz aumentada de un sistema lineal de ecuaciones. Entonces:
una variable que corresponde a un 1 inicial es una variable básica o dependiente, y
una variable que no corresponde a un 1 inicial es una variable libre o independiente.
Probablemente se pueda ver que “libre” e “independiente” son relativamente sinónimos. De ello se deduce que si una variable no es independiente, debe ser dependiente; la palabra “básica” proviene de conexiones con otras áreas de las matemáticas que aquí no exploraremos.
Estas definiciones nos ayudan a entender cuándo un sistema consistente de ecuaciones lineales tendrá infinitas soluciones. Si no hay variables libres, entonces hay exactamente una solución; si hay alguna variable libre, hay soluciones infinitas.
Un sistema lineal consistente de ecuaciones tendrá exactamente una solución si y solo si hay un 1 inicial para cada variable en el sistema.
Si un sistema lineal consistente de ecuaciones tiene una variable libre, tiene infinitas soluciones.
Si un sistema lineal consistente tiene más variables que 1s iniciales, entonces el sistema tendrá infinitas soluciones.
Un sistema lineal consistente con más variables que ecuaciones siempre tendrá infinitas soluciones.
La\(\PageIndex{1}\) Idea Clave se aplica solo a sistemas consistentes. Si un sistema es inconsistente, entonces no existe solución y hablar de variables libres y básicas no tiene sentido.
Cuando un sistema consistente tiene una sola solución, cada ecuación que proviene de la forma de escalón de fila reducida de la matriz aumentada correspondiente contendrá exactamente una variable. Si el sistema consistente tiene infinitas soluciones, entonces habrá al menos una ecuación proveniente de la forma de escalón de fila reducida que contiene más de una variable. La “primera” variable será la variable básica (o dependiente); todas las demás serán variables libres.
Ahora hemos visto ejemplos de sistemas consistentes con exactamente una solución y otras con infinitas soluciones. ¿Cómo reconoceremos que un sistema es inconsistente? Vamos a averiguarlo a través de un ejemplo.
Encuentre la solución al sistema lineal\[\begin{array}{ccccccc} x_1&+&x_2&+&x_3&=&1\\ x_1&+&2x_2&+&x_3&=&2\\ 2x_1&+&3x_2&+&2x_3&=&0\\ \end{array}. \nonumber \]
Solución
Comenzamos poniendo la matriz correspondiente en forma de escalón de fila reducida.
\[\left[\begin{array}{cccc}{1}&{1}&{1}&{1}\\{1}&{2}&{1}&{2}\\{2}&{3}&{2}&{0}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{cccc}{1}&{0}&{1}&{0}\\{0}&{1}&{0}&{0}\\{0}&{0}&{0}&{1}\end{array}\right] \nonumber \]
Ahora tomemos la matriz reducida y escribamos las ecuaciones correspondientes. Las dos primeras filas nos dan las ecuaciones\[\begin{align}\begin{aligned} x_1+x_3&=0\\ x_2 &= 0.\\ \end{aligned}\end{align} \nonumber \] Hasta el momento, tan buenas. Sin embargo la última fila nos da la ecuación\[0x_1+0x_2+0x_3 = 1 \nonumber \] o, de manera más concisa,\(0=1\). Obviamente, esto no es cierto; hemos llegado a una contradicción. Por lo tanto, no existe solución; este sistema es inconsistente.
En secciones anteriores solo hemos encontrado sistemas lineales con soluciones únicas (exactamente una solución). Ahora hemos visto tres ejemplos más con diferentes tipos de soluciones. Los dos primeros ejemplos de esta sección tuvieron infinitas soluciones, y el tercero no tuvo solución. ¿Cómo podemos saber si un sistema es inconsistente?
Un sistema lineal será inconsistente sólo cuando implique que 0 es igual a 1. Podemos decir si un sistema lineal implica esto poniendo su matriz aumentada correspondiente en forma de escalón de fila reducida. Si tenemos alguna fila donde todas las entradas sean 0 excepto la entrada en la última columna, entonces el sistema implica 0=1. Más sucintamente, si tenemos un 1 líder en la última columna de una matriz aumentada, entonces el sistema lineal no tiene solución.
Un sistema de ecuaciones lineales es inconsistente si la forma de escalón de fila reducida de su matriz aumentada correspondiente tiene un 1 inicial en la última columna.
Confirmar que el sistema lineal no\[\begin{array}{ccccc} x&+&y&=&0 \\2x&+&2y&=&4 \end{array} \nonumber \] tiene solución.
Solución
Podemos verificar que este sistema no tiene solución de dos maneras. Primero, pensémoslo. Si\(x+y=0\), entonces es razonable, multiplicando ambos lados de esta ecuación por 2, eso\(2x+2y = 0\). No obstante, la segunda ecuación de nuestro sistema lo dice\(2x+2y= 4\). Ya que\(0\neq 4\), tenemos una contradicción y por lo tanto nuestro sistema no tiene solución. (No podemos elegir valores para\(x\) y para que\(y\) sean\(2x+2y\) iguales tanto a 0 como a 4.)
Ahora confirmemos esto usando la técnica prescrita desde arriba. La forma de escalón de fila reducida de la matriz aumentada correspondiente es
\[\left[\begin{array}{ccc}{1}&{1}&{0}\\{0}&{0}&{1}\end{array}\right] \nonumber \]
Tenemos un 1 líder en la última columna, por lo que por lo tanto el sistema es inconsistente.
Resumamos lo que hemos aprendido hasta este punto. Considere la forma de escalón de fila reducida de la matriz aumentada de un sistema de ecuaciones lineales. \(^{1}\)Si hay un 1 líder en la última columna, el sistema no tiene solución. De lo contrario, si hay un 1 inicial para cada variable, entonces hay exactamente una solución; de lo contrario (es decir, hay variables libres) hay infinitas soluciones.
Los sistemas con exactamente una solución o ninguna solución son los más fáciles de tratar; los sistemas con soluciones infinitas son un poco más difíciles de manejar. Por lo tanto, haremos un poco más de práctica. Primero, una definición: si hay infinitas soluciones, ¿cómo llamamos una de esas infinitas soluciones?
Considera un sistema lineal de ecuaciones con infinitas soluciones. Una solución particular es una solución del conjunto infinito de soluciones posibles.
La manera más fácil de encontrar una solución en particular es elegir valores para las variables libres que luego determina los valores de las variables dependientes. Nuevamente, se pide más práctica.
Dar la solución a un sistema lineal cuya matriz aumentada en forma de escalón de fila reducida es
\[\left[\begin{array}{ccccc}{1}&{-1}&{0}&{2}&{4}\\{0}&{0}&{1}&{-3}&{7}\\{0}&{0}&{0}&{0}&{0}\end{array}\right] \nonumber \]
y dar dos soluciones particulares.
Solución
Esencialmente podemos ignorar la tercera fila; no divulga ninguna información sobre la solución. \(^{2}\)La primera y segunda filas se pueden reescribir como las siguientes ecuaciones:\[\begin{align}\begin{aligned} x_1 - x_2 + 2x_4 &=4 \\ x_3 - 3x_4 &= 7. \\ \end{aligned}\end{align} \nonumber \] Observe cómo las variables\(x_1\) y\(x_3\) corresponden a los 1s iniciales de la matriz dada. Por lo tanto\(x_1\) y\(x_3\) son variables dependientes; todas las demás variables (en este caso,\(x_2\) y\(x_4\)) son variables libres.
Generalmente escribimos nuestra solución con las variables dependientes a la izquierda y variables y constantes independientes a la derecha. También es una buena práctica reconocer que nuestras variables libres son, de hecho, libres. Así que nuestra solución final se vería algo así como\[\begin{align}\begin{aligned} x_1 &= 4 +x_2 - 2x_4 \\ x_2 & \text{ is free} \\ x_3 &= 7+3x_4 \\ x_4 & \text{ is free}.\end{aligned}\end{align} \nonumber \]
Para encontrar soluciones particulares, elija valores para nuestras variables gratuitas. No hay una forma “correcta” de hacer esto; somos “libres” de elegir lo que queramos.
Al establecer\(x_2 = 0 = x_4\), tenemos la solución\(x_1 = 4\),\(x_2 = 0\),\(x_3 = 7\),\(x_4 = 0\). Al establecer\(x_2 = 1\) y\(x_4 = -5\), tenemos la solución\(x_1 = 15\),\(x_2 = 1\),\(x_3 = -8\),\(x_4 = -5\). Es más fácil leer esto cuando se listan las variables verticalmente, por lo que repetimos estas soluciones:
Una solución particular es:
\[\begin{align}\begin{aligned} x_1 &= 4\\ x_2 &=0 \\ x_3 &= 7 \\ x_4 &= 0. \end{aligned}\end{align} \nonumber \]
Otra solución particular es:
\[\begin{align}\begin{aligned} x_1 &= 15\\ x_2 &=1 \\ x_3 &= -8 \\ x_4 &= -5. \end{aligned}\end{align} \nonumber \]
Encuentre la solución a un sistema lineal cuya matriz aumentada en forma de escalón de fila reducida es
\[\left[\begin{array}{ccccc}{1}&{0}&{0}&{2}&{3}\\{0}&{1}&{0}&{4}&{5}\end{array}\right] \nonumber \]
y dar dos soluciones particulares.
Solución
Convertir las dos filas en ecuaciones que tenemos\[\begin{align}\begin{aligned} x_1 + 2x_4 &= 3 \\ x_2 + 4x_4&=5.\\ \end{aligned}\end{align} \nonumber \]
Vemos eso\(x_1\) y\(x_2\) son nuestras variables dependientes, pues corresponden a los 1s principales. Por lo tanto,\(x_3\) y\(x_4\) son variables independientes. Esta situación se siente un poco inusual, \(^{3}\)pues\(x_3\) no aparece en ninguna de las ecuaciones anteriores, pero no puede pasarla por alto; sigue siendo una variable libre ya que no hay un 1 inicial que le corresponda. Escribimos nuestra solución como:\[\begin{align}\begin{aligned} x_1 &= 3-2x_4 \\ x_2 &=5-4x_4 \\ x_3 & \text{ is free} \\ x_4 & \text{ is free}. \\ \end{aligned}\end{align} \nonumber \]
Para encontrar dos soluciones particulares, elegimos valores para nuestras variables libres. Nuevamente, no hay una forma “correcta” de hacer esto (de hecho, hay\(\ldots\) infinitas formas de hacerlo) así que aquí solo damos un ejemplo.
Una solución particular es:
\[\begin{align}\begin{aligned} x_1 &= 3\\ x_2 &=5 \\ x_3 &= 1000 \\ x_4 &= 0. \end{aligned}\end{align} \nonumber \]
Otra solución particular es:
\[\begin{align}\begin{aligned} x_1 &= 3-2\pi\\ x_2 &=5-4\pi \\ x_3 &= e^2 \\ x_4 &= \pi. \end{aligned}\end{align} \nonumber \]
(En la segunda solución particular elegimos valores “inusuales” para\(x_3\) y\(x_4\) solo para resaltar el hecho de que podemos.)
Encuentre la solución al sistema lineal\[\begin{array}{ccccccc}x_1&+&x_2&+&x_3&=&5\\x_1&-&x_2&+&x_3&=&3\\ \end{array} \nonumber \] y dé dos soluciones particulares.
Solución
La matriz aumentada correspondiente y su forma de escalón de fila reducida se dan a continuación.
\[\left[\begin{array}{cccc}{1}&{1}&{1}&{5}\\{1}&{-1}&{1}&{3}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{cccc}{1}&{0}&{1}&{4}\\{0}&{1}&{0}&{1}\end{array}\right] \nonumber \]
Convirtiendo estas dos filas en ecuaciones, nos hemos\[\begin{align}\begin{aligned} x_1+x_3&=4\\x_2&=1\\ \end{aligned}\end{align} \nonumber \] dado la solución\[\begin{align}\begin{aligned} x_1&= 4-x_3\\x_2&=1\\x_3 &\text{ is free}.\\ \end{aligned}\end{align} \nonumber \]
Una vez más, obtenemos una solución un poco “inusual”; si bien\(x_2\) es una variable dependiente, no depende de ninguna variable libre; en cambio, siempre es 1. (Podemos pensar en ello como dependiendo del valor de 1.) Al elegir dos valores para\(x_3\), obtenemos dos soluciones particulares.
Una solución particular es:
\[\begin{align}\begin{aligned} x_1 &= 4\\ x_2 &=1 \\ x_3 &= 0 . \end{aligned}\end{align} \nonumber \]
Otra solución particular es:
\[\begin{align}\begin{aligned} x_1 &= 3\\ x_2 &=1 \\ x_3 &= 1 . \end{aligned}\end{align} \nonumber \]
Las constantes y coeficientes de una matriz trabajan juntos para determinar si un sistema dado de ecuaciones lineales tiene una, infinita o ninguna solución. El concepto se desarrollará más en capítulos posteriores, pero en definitiva, los coeficientes determinan si una matriz tendrá exactamente una solución o no. En el caso “o no”, las constantes determinan si existen o no soluciones infinitas o ninguna solución. (Entonces, si un sistema lineal dado tiene exactamente una solución, siempre tendrá exactamente una solución incluso si se cambian las constantes). Veamos un ejemplo para hacernos una idea de cómo funcionan juntos los valores de constantes y coeficientes para determinar el tipo de solución.
¿Para qué valores de\(k\) tendrá el sistema dado exactamente una solución, infinitas soluciones o ninguna solución? \[\begin{array}{ccccc}x_1&+&2x_2&=&3\\ 3x_1&+&kx_2&=&9\end{array} \nonumber \]
Solución
Respondemos a esta pregunta formando la matriz aumentada e iniciando el proceso de ponerla en forma de escalón de fila reducida. A continuación vemos la matriz aumentada y una operación de fila elemental que inicia el proceso de eliminación gaussiana.
\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{3}&{k}&{9}\end{array}\right]\qquad\overrightarrow{-3R_{1}+R_{2}\to R_{2}}\qquad\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{k-6}&{0}\end{array}\right] \nonumber \]
Esto es lo más lejos que tenemos que llegar. Al mirar la segunda fila, vemos que si\(k=6\), entonces esa fila contiene sólo ceros y\(x_2\) es una variable libre; tenemos infinitas soluciones. Si\(k\neq 6\), entonces nuestro siguiente paso sería hacer que esa entrada de segunda fila, segunda columna sea una inicial. No nos importa particularmente la solución, solo que tendríamos exactamente una como ambas\(x_1\) y\(x_2\) corresponderíamos a una líder y por lo tanto serían variables dependientes.
Nuestro análisis final es entonces este. Si\(k\neq 6\), hay exactamente una solución; si\(k=6\), hay infinitas soluciones. En este ejemplo, no es posible no tener soluciones.
Como extensión del ejemplo anterior, consideremos la matriz aumentada similar donde la constante 9 es reemplazada por una 10. Realizar la misma operación de fila elemental da
\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{3}&{k}&{10}\end{array}\right]\qquad\overrightarrow{-3R_{1}+R_{2}\to R_{2}}\qquad\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{k-6}&{1}\end{array}\right] \nonumber \]
Como en el ejemplo anterior, si\(k\neq6\), podemos hacer que la segunda fila, la segunda columna ingrese una inicial y de ahí tengamos una solución. No obstante, si\(k=6\), entonces nuestra última fila es\([0\ 0\ 1]\), es decir, no tenemos solución.
Hemos estado estudiando las soluciones a sistemas lineales principalmente en un entorno “académico”; hemos estado resolviendo sistemas por el bien de resolver sistemas. En la siguiente sección, veremos situaciones que crean sistemas lineales que necesitan resolución (es decir, “problemas de palabras”).
Notas al pie
[1] Eso seguro parece un bocado en sí mismo. No obstante, se reduce a “mirar la forma reducida de la matriz habitual”.
[2] Entonces, ¿por qué incluirlo? Las filas de ceros a veces aparecen “inesperadamente” en las matrices después de que se han puesto en forma de escalón de fila reducida. Cuando esto sucede, sí aprendemos algo; significa que al menos una ecuación era una combinación de algunas de las otras.
[3] ¿Qué tipo de situación conduciría a una columna de todos los ceros? Para tener tal columna, la matriz original necesitaba tener una columna de todos los ceros, es decir, que si bien reconocíamos la existencia de una determinada variable, nunca la usamos realmente en ninguna ecuación. En términos prácticos, podríamos responder quitando la columna correspondiente de la matriz y solo tener en cuenta que esa variable es libre. En sistemas muy grandes, podría ser difícil determinar si realmente se usa o no una variable y uno no se preocuparía por ello.
Cuando aprendamos sobre s y s, veremos que bajo ciertas circunstancias surge esta situación. En esos casos dejamos la variable en el sistema solo para recordarnos que está ahí.


