3.4: Propiedades del Determinante

Objetivos de aprendizaje

• Tener la opción de calcular el determinante de una matriz usando la expansión de cofactores a lo largo de cualquier fila o columna es más útil cuando hay mucho de lo que en una fila o columna?
• ¿Qué operación de fila elemental no cambia el determinante de una matriz?
• ¿Por qué los matemáticos raramente sonríen?
• T/F: Cuando se utilizan computadoras para calcular el determinante de una matriz, rara vez se usa expansión de cofactores.

En la sección anterior aprendimos a calcular el determinante. En esta sección aprendemos algunas de las propiedades del determinante, y esto nos permitirá calcular los determinantes con mayor facilidad. En la siguiente sección veremos una aplicación de determinantes.

Comenzamos con un teorema que nos da más libertad a la hora de computar determinantes.

Teorema\(\PageIndex{1}\)

Expansión del cofactor a lo largo de cualquier fila o columna

\(A\)Déjese ser una\(n\times n\) matriz. El determinante de\(A\) puede calcularse usando expansión de cofactores a lo largo de cualquier fila o columna de\(A\).

Aludimos a este hecho atrás después del Ejemplo 3.3.3. Acabábamos de aprender qué era la expansión del cofactor y practicamos a lo largo de la segunda fila y bajamos por la tercera columna. Posteriormente, encontramos el determinante de esta matriz calculando la expansión del cofactor a lo largo de la primera fila. En los tres casos, conseguimos el número\(0\). Esto no fue una coincidencia. El teorema anterior establece que las tres expansiones en realidad estaban computando el determinante.

¿Cómo nos ayuda esto? Al darnos libertad para elegir cualquier fila o columna para usar para la expansión, podemos elegir una fila o columna que se vea “más atractiva”. Esto generalmente significa “tiene muchos ceros”. A continuación demostramos este principio.

Ejemplo\(\PageIndex{1}\)

Encuentra el determinante de

\[A=\left[\begin{array}{cccc}{1}&{2}&{0}&{9}\\{2}&{-3}&{0}&{5}\\{7}&{2}&{3}&{8}\\{-4}&{1}&{0}&{2}\end{array}\right]. \nonumber \]

Solución

Nuestra primera reacción bien puede ser “¡Oh, no! ¡No otro\(4\times 4\) determinante!” Sin embargo, podemos usar expansión de cofactores a lo largo de cualquier fila o columna que elijamos. La tercera columna se ve muy bien; tiene muchos ceros en ella. La expansión del cofactor a lo largo de esta columna es\[\begin{align}\begin{aligned} \text{det}(A) & = a_{1,3}C_{1,3} + a_{2,3}C_{2,3} + a_{3,3}C_{3,3}+a_{4,3}C_{4,3} \\ &= 0\cdot C_{1,3} + 0\cdot C_{2,3} + 3\cdot C_{3,3} + 0\cdot C_{4,3}\end{aligned}\end{align} \nonumber \]

Lo maravilloso aquí es que tres de nuestros cofactores se multiplican por\(0\). No vamos a molestarnos en computarlos ya que no van a contribuir al determinante. Así

\[\begin{align}\begin{aligned}\text{det}(A)&=3\cdot C_{3,3} \\ &=3\cdot (-1)^{3+3}\cdot\left|\begin{array}{ccc}{1}&{2}&{9}\\{2}&{-3}&{5}\\{-4}&{1}&{2}\end{array}\right| \\ &=3\cdot (-147)\quad\left(\begin{array}{c}{\text{we computed the determinant of the }3\times 3\text{ matrix}} \\ {\text{without showing our work; it is }-147}\end{array}\right) \\ &=-447\end{aligned}\end{align} \nonumber \]

Guau. Eso fue mucho más sencillo que computar todo lo que hicimos en el Ejemplo 3.3.6. Por supuesto, en ese ejemplo, en realidad no teníamos ningún atajo que pudiéramos haber empleado.

Ejemplo\(\PageIndex{2}\)

Encuentra el determinante de

\[A=\left[\begin{array}{ccccc}{1}&{2}&{3}&{4}&{5}\\{0}&{6}&{7}&{8}&{9}\\{0}&{0}&{10}&{11}&{12}\\{0}&{0}&{0}&{13}&{14} \\ {0}&{0}&{0}&{0}&{15}\end{array}\right]. \nonumber \]

Solución

A primera vista, pensamos “¡No quiero encontrar el determinante de una\(5\times 5\) matriz!” Sin embargo, usando nuestro conocimiento recién descubierto, vemos que las cosas no están tan mal. De hecho, este problema es muy fácil.

¿Qué fila o columna debemos elegir para encontrar el determinante a lo largo? Hay dos opciones obvias: la primera columna o la última fila. Ambos tienen 4 ceros en ellos. Elegimos la primera columna. \(^{1}\)Omitimos la mayor parte de la expansión del cofactor, ya que la mayor parte es simplemente\(0\):

\[\text{det}(A)=1\cdot (-1)^{1+1}\cdot\left|\begin{array}{cccc}{6}&{7}&{8}&{9}\\{0}&{10}&{11}&{12}\\{0}&{0}&{13}&{14}\\{0}&{0}&{0}&{15}\end{array}\right|. \nonumber \]

De igual manera, este determinante no es malo para calcular; nuevamente elegimos usar la expansión de cofactores a lo largo de la primera columna. Nota: técnicamente, esta expansión del cofactor es\(6\cdot(-1)^{1+1}A_{1,1}\); vamos a dejar caer los\((-1)^{1+1}\) términos de aquí en adelante en este ejemplo (va a aparecer mucho...).

\[\text{det}(A)=1\cdot 6\cdot\left|\begin{array}{ccc}{10}&{11}&{12}\\{0}&{13}&{14}\\{0}&{0}&{15}\end{array}\right|. \nonumber \]

Probablemente puedas ver una tendencia. Terminaremos los pasos sin explicar cada uno.

\[\begin{align}\begin{aligned}\text{det}(A)&=1\cdot 6\cdot 10\cdot\left|\begin{array}{cc}{13}&{14}\\{0}&{15}\end{array}\right| \\ &=1\cdot 6\cdot 10\cdot 13\cdot 15 \\ &=11700\end{aligned}\end{align} \nonumber \]

Vemos que el determinante final es el producto de las entradas diagonales. Esto funciona para cualquier matriz triangular (y como las matrices diagonales son triangulares, también funciona para matrices diagonales). Esta es una idea lo suficientemente importante como para que la pongamos en una caja.

Idea Clave\(\PageIndex{1}\): The Determinant of Triangular Matrices

El determinante de una matriz triangular es el producto de sus elementos diagonales.

Ahora es otra vez el momento de empezar a pensar como matemático. Recuerden, los matemáticos ven algo nuevo y a menudo preguntan “¿Cómo se relaciona esto con cosas que ya conozco?” Entonces ahora nos preguntamos: “Si cambiamos una matriz de alguna manera, ¿cómo se cambia su determinante?”

La forma estándar en que cambiamos matrices es a través de operaciones de fila elemental. Si realizamos una operación de fila elemental en una matriz, ¿cómo se comparará el determinante de la nueva matriz con el determinante de la matriz original?

Experimentemos primero y después declararemos oficialmente lo que sucede.

Ejemplo\(\PageIndex{3}\)

Let

\[A=\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]. \nonumber \]

Dejar\(B\) formarse a partir\(A\) de hacer una de las siguientes operaciones de fila elemental:

1. \(2R_{1}+R_{2}\to R_{2}\)
2. \(5R_{1}\to R_{1}\)
3. \(R_{1}\leftrightarrow R_{2}\)

Encuentra así\(\text{det}(A)\) como\(\text{det}(B)\) para cada una de las operaciones de fila anteriores.

Solución

Es sencillo de calcular\(\text{det}(A) = -2\).

Dejar que\(B\) se forme realizando la operación de fila en 1) en\(A\); así

\[B=\left[\begin{array}{cc}{1}&{2}\\{5}&{8}\end{array}\right]. \nonumber \]

Es claro que\(\text{det}(B) = -2\), lo mismo que\(\text{det}(A)\).

Ahora\(B\) déjese formar realizando la operación de fila elemental en 2) on\(A\); es decir,

\[B=\left[\begin{array}{cc}{5}&{10}\\{3}&{4}\end{array}\right]. \nonumber \]

Podemos ver eso\(\text{det}(B) = -10\), que es\(5\cdot\text{det}(A)\).

Finalmente,\(B\) déjese formar por la operación de tercera fila dada; intercambiar las dos filas de\(A\). Vemos que

\[B=\left[\begin{array}{cc}{3}&{4}\\{1}&{2}\end{array}\right] \nonumber \]

y eso\(\text{det}(B) = 2\), que es\((-1)\cdot\text{det}(A)\).

Hemos visto en el ejemplo anterior que parece haber una relación entre los determinantes de las matrices “antes y después” que son cambiadas por operaciones elementales de fila. Ciertamente, un ejemplo no es suficiente para basar una teoría, y aún no hemos probado nada. Independientemente, el siguiente teorema es cierto.

Teorema\(\PageIndex{2}\)

El Determinante y las Operaciones de Fila Primaria

Dejar\(A\) ser una\(n\times n\) matriz y dejar que\(B\) se forme realizando una operación de fila elemental en\(A\).

1. Si\(B\) se forma a partir\(A\) de la adición de un múltiplo escalar de una fila a otra, entonces\(\text{det}(B) = \text{det}(A)\).
2. Si\(B\) se forma a partir de\(A\) multiplicar una fila de\(A\) por un escalar\(k\), entonces\(\text{det}(B) = k\cdot\text{det}(A)\).
3. Si\(B\) se forma a partir de\(A\) intercambiando dos filas de\(A\), entonces\(\text{det}(B) = −\text{det}(A)\).

Pongamos este teorema a usar en un ejemplo.

Ejemplo\(\PageIndex{4}\)

Let

\[A=\left[\begin{array}{ccc}{1}&{2}&{1}\\{0}&{1}&{1}\\{1}&{1}&{1}\end{array}\right]. \nonumber \]

Calcular\(\text{det}(A)\), luego encontrar los determinantes de las siguientes matrices mediante inspección usando Teorema\(\PageIndex{2}\).

\[B=\left[\begin{array}{ccc}{1}&{1}&{1}\\{1}&{2}&{1}\\{0}&{1}&{1}\end{array}\right]\quad C=\left[\begin{array}{ccc}{1}&{2}&{1}\\{0}&{1}&{1}\\{7}&{7}&{7}\end{array}\right]\quad D=\left[\begin{array}{ccc}{1}&{-1}&{-2}\\{0}&{1}&{1}\\{1}&{1}&{1}\end{array}\right] \nonumber \]

Solución

La computación\(\text{det}(A)\) por expansión de cofactores hacia abajo de la primera columna o a lo largo de la segunda fila parece ser la mejor opción, utilizando el cero en la matriz. Podemos confirmarlo rápidamente\(\text{det}(A) = 1\).

Para calcular\(\text{det}(B)\), observe que las filas de\(A\) fueron reordenadas para formar\(B\). Hay diferentes formas de describir lo que sucedió; dicho\(R_1\leftrightarrow R_2\) fue seguido por\(R_1\leftrightarrow R_3\) produce\(B\) de\(A\). Ya que hubo dos swaps de fila,\(\text{det}(B) = (-1)(-1)\text{det}(A) = \text{det}(A) = 1\).

Observe que\(C\) se forma\(A\) a partir de multiplicar la tercera fila por\(7\). Por lo tanto\(\text{det}(C) = 7\cdot\text{det}(A) = 7\).

Se necesita un poco de reflexión, pero podemos formarnos\(D\) a partir de\(A\) por la operación\(-3R_2+R_1\rightarrow R_1\). Este tipo de operación de fila elemental no cambia los determinantes, por lo que\(\text{det}(D) = \text{det}(A)\).

Sigamos pensando como matemáticos; los matemáticos tienden a recordar “problemas” que han encontrado en el pasado, \(^{2}\)y cuando aprenden algo nuevo, en el fondo de sus mentes intentan aplicar sus nuevos conocimientos para resolver su viejo problema.

¿Qué “problema” descubrimos recientemente? Afirmamos en el último capítulo que incluso las computadoras no podían computar el determinante de matrices grandes con expansión de cofactores. ¿Cómo entonces podemos calcular el determinante de las matrices grandes?

Acabamos de aprender dos datos interesantes y útiles sobre los determinantes matriciales. Primero, el determinante de una matriz triangular es fácil de calcular: simplemente multiplicar los elementos diagonales. En segundo lugar, sabemos cómo las operaciones elementales de fila afectan al determinante. Juntar estas dos ideas: dada cualquier matriz cuadrada, podemos usar operaciones de fila elemental para poner la matriz en forma triangular, \(^{3}\)encontrar el determinante de la nueva matriz (lo cual es fácil) y luego ajustar ese número recordando qué operaciones elementales realizamos. Practicemos esto.

Ejemplo\(\PageIndex{5}\)

Encuentra el determinante de\(A\) poniéndolo primero\(A\) en una forma triangular, donde

\[A=\left[\begin{array}{ccc}{2}&{4}&{-2}\\{-1}&{-2}&{5}\\{3}&{2}&{1}\end{array}\right]. \nonumber \]

Solución

Al\(A\) poner en forma triangular, no necesitamos preocuparnos por conseguir liderar\(1\) s, sino que tiende a facilitarnos la vida a medida que resolvemos un problema a mano. Así que vamos a escalar la primera fila por\(1/2\):

\[\frac{1}{2}R_{1}\to R_{1}\quad\left[\begin{array}{ccc}{1}&{2}&{-1}\\{-1}&{-2}&{5}\\{3}&{2}&{1}\end{array}\right]. \nonumber \]

Ahora vamos a obtener\(0\) s por debajo de este líder\(1\):

\[\begin{array}{c}{R_{1}+R_{2}\to R_{2}}\\{-3R_{1}+R_{3}\to R_{3}}\end{array}\quad\left[\begin{array}{ccc}{1}&{2}&{-1}\\{0}&{0}&{4}\\{0}&{-4}&{4}\end{array}\right]. \nonumber \]

Podemos terminar en un solo paso; intercambiando filas\(2\) y\(3\) tendremos nuestra matriz en forma triangular.

\[R_{2}\leftrightarrow R_{3}\quad\left[\begin{array}{ccc}{1}&{2}&{-1}\\{0}&{-4}&{4}\\{0}&{0}&{4}\end{array}\right]. \nonumber \]

Vamos a nombrar esta última matriz\(B\). El determinante de\(B\) es fácil de calcular ya que es triangular;\(\text{det}(B) = -16\). Podemos usar esto para encontrar\(\text{det}(A)\).

Recordemos los pasos en los que nos\(A\) transformamos\(B\). Ellos son:

\[\frac 12R_1 \rightarrow R_1 \nonumber \]

\[R_1 + R_2 \rightarrow R_2 \nonumber \]

\[-3R_1+R_3\rightarrow R_3 \nonumber \]

\[R_2 \leftrightarrow R_3 \nonumber \]

La primera operación multiplicó una fila de\(A\) por\(\frac 12\). Esto significa que la matriz resultante tuvo un determinante que fue\(\frac12\) el determinante de\(A\).

Las dos operaciones siguientes no afectaron en absoluto al determinante. La última operación, el intercambio de filas, cambió el letrero. Combinando estos efectos, sabemos que\[-16 = \text{det}(B)= (-1)\frac12\text{det}(A). \nonumber \]

Resolviendo para eso\(\text{det}(A)\) tenemos\(\text{det}(A)=32\).

En la práctica, no necesitamos hacer un seguimiento de las operaciones donde agregamos múltiplos de una fila a otra; simplemente no afectan al determinante. Además, en la práctica, estos pasos los lleva a cabo una computadora, y a las computadoras no les importa liderar 1s. Por lo tanto, rara vez se utilizan operaciones de escalado de filas Lo único que hay que hacer un seguimiento son los swaps de filas, e incluso entonces lo único que nos importa es el número de swaps de filas. Un número impar de swaps de filas significa que el determinante original tiene el signo opuesto de la matriz de forma triangular; un número par de swaps de fila significa que tienen el mismo determinante.

Practicemos esto de nuevo.

Ejemplo\(\PageIndex{6}\)

La matriz\(B\) se formó a partir del\(A\) uso de las siguientes operaciones elementales de fila, aunque no necesariamente en este orden. Encuentra\(\text{det}(A)\).

\[B=\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{4}&{5}\\{0}&{0}&{6}\end{array}\right] \quad\begin{array}{c}{2R_{1}\to R_{1}} \\ {\frac{1}{3}R_{3}\to R_{3}} \\ {R_{1}\leftrightarrow R_{2}} \\ {6R_{1}+R_{2}\to R_{2}}\end{array} \nonumber \]

Solución

Es fácil de calcular\(\text{det}(B)=24\). In looking at our list of elementary row operations, we see that only the first three have an effect on the determinant. Therefore

\[24=\text{det}(B)=2\cdot\frac{1}{3}\cdot (-1)\cdot\text{det}(A) \nonumber \]

y por lo tanto

\[\text{det}(A)=-36. \nonumber \]

En el ejemplo anterior, es posible que hayamos tenido la tentación de “reconstruir”\(A\) usando las operaciones de fila elemental y luego calcular el determinante. Esto se puede hacer, pero en general es una mala idea; se necesita demasiado trabajo y es demasiado fácil cometer un error.

Pensemos un poco más como un matemático. ¿Cómo funciona el determinante con otras operaciones matriciales que conocemos? Específicamente, ¿cómo interactúa el determinante con la adición de matriz, la multiplicación escalar, la multiplicación matricial, la transposición y la traza? Nuevamente haremos un ejemplo para hacernos una idea de lo que está pasando, luego daremos un teorema para afirmar lo que es verdad.

Ejemplo\(\PageIndex{7}\)

Let

\[A=\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]\quad\text{and}\quad B=\left[\begin{array}{cc}{2}&{1}\\{3}&{5}\end{array}\right]. \nonumber \]

Encuentre los determinantes de las matrices\(A\)\(B\),\(A + B\),\(3A\),\(AB\),\(A^{T}\),\(A^{−1}\), y compare el determinante de estas matrices con su rastro.

Solución

Podemos calcular rápidamente eso\(\text{det}(A) = -2\) y aquello\(\text{det}(B) = 7\).

\[\begin{align}\begin{aligned}\text{det}(A-B)&=\text{det}\left(\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]-\left[\begin{array}{cc}{2}&{1}\\{3}&{5}\end{array}\right]\right) \\ &=\left|\begin{array}{cc}{-1}&{1}\\{0}&{-1}\end{array}\right| \\ &=1\end{aligned}\end{align} \nonumber \]

Es difícil encontrar una conexión entre\(\text{det}(A-b)\),\(\text{det}(A)\) y\(\text{det}(B)\).

\[\begin{align}\begin{aligned}\text{det}(3A)&=\left|\begin{array}{cc}{3}&{6}\\{9}&{12}\end{array}\right| \\ &=-18\end{aligned}\end{align} \nonumber \]

Podemos resolverlo; multiplicar una fila de\(A\) por\(3\) aumenta el determinante por un factor de\(3\); hacerlo de nuevo (y por lo tanto multiplicar ambas filas por\(3\)) aumenta nuevamente el determinante por un factor de\(3\). Por lo tanto\(\text{det}(3A)=3\cdot 3\cdot\text{det}(A)\), o\(3^{2}\cdot A\).

\[\begin{align}\begin{aligned}\text{det}(AB)&=\text{det}\left(\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]\left[\begin{array}{cc}{2}&{1}\\{3}&{5}\end{array}\right]\right) \\ &=\left|\begin{array}{cc}{8}&{11}\\{18}&{23}\end{array}\right| \\ &=-14\end{aligned}\end{align} \nonumber \]

Este parece claro;\(\text{det}(AB)=\text{det}(A)\text{det}(B)\).

\[\begin{align}\begin{aligned}\text{det}(A^{T})&=\left|\begin{array}{cc}{1}&{3}\\{2}&{4}\end{array}\right| \\ &=-2\end{aligned}\end{align} \nonumber \]

Obviamente\(\text{det}(A^{T})=\text{det}(A)\); ¿este siempre va a ser el caso? Si lo pensamos, podemos ver que la expansión del cofactor a lo largo de la primera fila de nos\(A\) dará el mismo resultado que la expansión del cofactor a lo largo de la primera columna de\(A\). \(^{4}\)

\[\begin{align}\begin{aligned}\text{det}(A^{-1})&=\left|\begin{array}{cc}{-2}&{1}\\{3/2}&{-1/2}\end{array}\right| \\ &=1-3/2 \\ &=-1/2\end{aligned}\end{align} \nonumber \]

Parece como si

\[\text{det}(A^{-1})=\frac{1}{\text{det}(A)}. \nonumber \]

Terminamos remarcando que no parece haber conexión alguna entre el rastro de una matriz y su determinante. Dejamos al lector calcular el rastro para algunas de las matrices anteriores y confirmar esta afirmación.

Ahora declaramos un teorema que confirmará nuestras conjeturas del ejemplo anterior.

Teorema\(\PageIndex{3}\)

Propiedades Determinantes

Dejar\(A\) y\(B\) ser\(n\times n\) matrices y dejar que\(k\) sea un escalador. Lo siguiente es cierto:

1. \(\text{det}(kA)=k^{n}\cdot\text{det}(A)\)
2. \(\text{det}(A^{T})=\text{det}(A)\)
3. \(\text{det}(AB)=\text{det}(A)\text{det}(B)\)
4. Si\(A\) es invertible, entonces
   \[\text{det}(A^{-1})=\frac{1}{\text{det}(A)}.\nonumber \]
5. Una matriz\(A\) es invertible si y solo si\(\text{det}(A)\neq 0\).

Esta última afirmación del teorema anterior es significativa: ¿qué pasa si\(\text{det}(A) = 0\)? Parece que\(\text{det}(A^{-1})="1/0"\), que no está definido. En realidad no hay problema aquí; resulta que si\(\text{det}(A)=0\), entonces no\(A\) es invertible (de ahí la parte 5 del Teorema\(\PageIndex{3}\)). Esto nos permite sumar a nuestro Teorema de Matriz Invertible.

Teorema\(\PageIndex{4}\)

Teorema de Matriz Invertible

\(A\)Déjese ser una\(n\times n\) matriz. Las siguientes declaraciones son equivalentes.

1. \(A\)es invertible.
2. \(\text{det}(A)\neq 0\).

Esta nueva adición al Teorema de Matriz Invertible es muy útil; volveremos a referirnos a ella en el Capítulo 4 cuando discutamos los valores propios.

Terminamos esta sección con un atajo para computar los determinantes de\(3\times 3\) las matrices. Considera la matriz\(A\):

\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{4}&{5}&{6}\\{7}&{8}&{9}\end{array}\right]. \nonumber \]

Podemos calcular su determinante usando expansión de cofactores como hicimos en el Ejemplo 3.3.4. Una vez que uno se vuelve competente en este método, calcular el determinante de a\(3\times3\) no es tan difícil. Un método que muchos encuentran más fácil, sin embargo, comienza con reescribir la matriz sin los corchetes, y repitiendo la primera y segunda columnas al final como se muestra a continuación. \[\begin{array}{ccccc} 1&2&3&1&2 \\ 4 & 5 & 6&4&5\\7&8&9&7&8\end{array} \nonumber \]

En esta\(3\times 5\) matriz de números, hay 3 diagonales completas “superior izquierda a inferior derecha”, y 3 diagonales completas de “superior derecha a inferior izquierda”, como se muestra a continuación con las flechas.

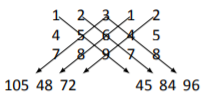
Los números que aparecen en los extremos de cada una de las flechas se calculan multiplicando los números encontrados a lo largo de las flechas. Por ejemplo, el\(105\) viene de multiplicar\(3\cdot5\cdot7=105\). El determinante se encuentra sumando los números de la derecha y restando la suma de los números de la izquierda. Es decir,\[\text{det}(A) = (45+84+96) - (105+48+72) = 0. \nonumber \]

Para ayudarnos a recordar este atajo, lo convertiremos en una Idea Clave.

Idea Clave\(\PageIndex{2}\): \(3\times 3\) Determinant Shortcut

\(A\)Déjese ser una\(3\times 3\) matriz. Cree una\(3\times 5\) matriz repitiendo las primeras\(2\) columnas y considere los productos de las diagonales\(3\) “derecha” y las diagonales de\(3\) “mano izquierda” como se muestra anteriormente. Entonces

\[\begin{align}\begin{aligned}\text{det}(A)&=\text{"(the sum of the right hand numbers)} \\ & -\text{(the sum of the left hand numbers)".}\end{aligned}\end{align} \nonumber \]

Practicaremos una vez más en el contexto de un ejemplo.

Ejemplo\(\PageIndex{8}\)

Encuentre el determinante de\(A\) usar el atajo descrito anteriormente, donde

\[A=\left[\begin{array}{ccc}{1}&{3}&{9}\\{-2}&{3}&{4}\\{-5}&{7}&{2}\end{array}\right]. \nonumber \]

Solución

Reescribiendo la primera\(2\) columns, drawing the proper diagonals, and multiplying, we get:

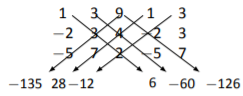
Sumando los números de la derecha y restando la suma de los números de la izquierda, obtenemos\[\text{det}(A) = (6-60-126) - ( -135+28-12) = -61. \nonumber \]

In the next section we’ll see how the determinant can be used to solve systems of linear equations.

Footnotes

[1] We do not choose this because it is the better choice; both options are good. We simply had to make a choice.

[2] which is why mathematicians rarely smile: they are remembering their problems

[3] or echelon form

[4] This can be a bit tricky to think out in your head. Try it with a 3\(\times 3\) matrix \(A\) and see how it works. All the \(2\times 2\) submatrices that are created in \(A^{T}\) are the transpose of those found in \(A\); this doesn’t matter since it is easy to see that the determinant isn’t affected by the transpose in a \(2\times 2\) matrix.