5.1: Transformaciones del Plano Cartesiano

Última actualización
Guardar como PDF

Page ID: 116530

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Para entender cómo el plano cartesiano se ve afectado por la multiplicación por una matriz, ayuda a estudiar cómo se ve afectado ¿qué es lo que se ve afectado?
Transformar el plano cartesiano a través de la multiplicación matricial transforma las líneas rectas en ¿qué tipo de líneas?
T/F: Si se dibuja una imagen de una oveja en el plano cartesiano, después se transforma el plano usando la matriz
\[\left[\begin{array}{cc}{-1}&{0}\\{0}&{1}\end{array}\right], \nonumber \]
se podría decir que la oveja fue “esquilada.

Se estudió en la Sección 2.3 cómo visualizar vectores y cómo se pueden representar gráficamente ciertas operaciones aritméticas matriciales. Limitamos nuestra comprensión visual de la multiplicación matricial a graficar un vector, multiplicarlo por una matriz y luego graficar el vector resultante. En esta sección exploraremos estas ideas de multiplicación con mayor profundidad. En lugar de multiplicar vectores individuales por una matriz$A$, estudiaremos qué sucede cuando multiplicamos por cada vector en los planes cartesianos$A$. $^{1}$

Debido a la Propiedad Distributiva, demostrada hace mucho tiempo en el Ejemplo 2.3.11, podemos decir que el plano cartesiano se transformará de una manera muy agradable, predecible. Las líneas rectas se transformarán en otras líneas rectas (y no se volverán curvas, ni dentadas, ni rotas). Las líneas curvas se transformarán en otras líneas curvas (quizás la curva se volverá “recta”, pero no se volverá irregular o quebrada).

Una forma de estudiar cómo todo el plano cartesiano se ve afectado por la multiplicación por una matriz$A$ es estudiar cómo se ve afectado el cuadrado unitario. El cuadrado unitario es el cuadrado con esquinas en los puntos$(0,0)$,$(1,0)$,$(1,1)$, y$(0,1)$. Cada esquina puede ser representada por el vector que apunta a ella; multiplicar cada uno de estos vectores por$A$ y podemos hacernos una idea de cómo$A$ afecta a todo el plano cartesiano.

Vamos a probar un ejemplo.

Ejemplo$\PageIndex{1}$

Trazar los vectores del cuadrado unitario antes y después de que hayan sido multiplicados por$A$, donde

\[A=\left[\begin{array}{cc}{1}&{4}\\{2}&{3}\end{array}\right]. \nonumber \]

Solución

Las cuatro esquinas de la unidad cuadrada pueden ser representadas por los vectores

\[\left[\begin{array}{c}{0}\\{0}\end{array}\right],\quad\left[\begin{array}{c}{1}\\{0}\end{array}\right],\quad\left[\begin{array}{c}{1}\\{1}\end{array}\right],\quad\left[\begin{array}{c}{0}\\{1}\end{array}\right]. \nonumber \]

Multiplicar cada uno por$A$ da los vectores

\[\left[\begin{array}{c}{0}\\{0}\end{array}\right],\quad\left[\begin{array}{c}{1}\\{2}\end{array}\right],\quad\left[\begin{array}{c}{5}\\{5}\end{array}\right],\quad\left[\begin{array}{c}{4}\\{3}\end{array}\right]. \nonumber \]

respectivamente.

(Pista: una forma de usar tu calculadora para hacer esto por ti rápidamente es hacer una$2\times 4$ matriz cuyas columnas sean cada uno de estos vectores. En este caso, crear una matriz

\[B=\left[\begin{array}{cccc}{0}&{1}&{1}&{0}\\{0}&{0}&{1}&{1}\end{array}\right]. \nonumber \]

Luego multiplique$B$ por$A$ y lea los vectores transformados de las columnas respectivas:

\[AB=\left[\begin{array}{cccc}{0}&{1}&{5}&{4}\\{0}&{2}&{5}&{3}\end{array}\right]. \nonumber \]

Esto ahorra tiempo, especialmente si realiza un procedimiento similar para múltiples matrices$A$. Por supuesto, podemos ahorrar más tiempo omitiendo la primera columna; ya que es la columna de ceros, quedará la columna de ceros después de multiplicar por$A$.)

El cuadrado unitario y su transformación se grafican en la Figura$\PageIndex{1}$, donde los vértices conformados se corresponden entre sí a través de las dos gráficas. Observe cómo el cuadrado se convirtió en algún tipo de cuadrilátero (en realidad es un paralelogramo). Algo realmente interesante es cómo los vértices triangulares y cuadrados parecen haber cambiado de lugar —es como si el cuadrado, además de estar estirado fuera de forma, se volteó.

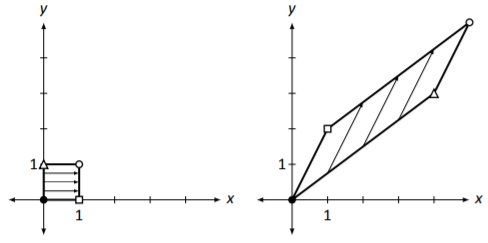
$clipboard_ee653c51c10d0511e537d75cd4beaa05c.png$

Figura$\PageIndex{1}$: Transformar el cuadrado unitario por multiplicación matricial en Ejemplo$\PageIndex{1}$.

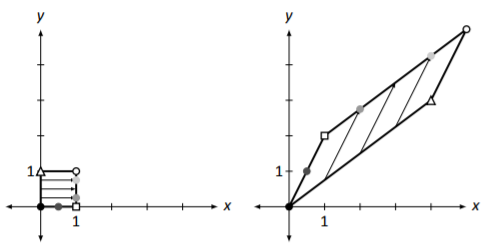
$clipboard_ebdb152c9ef703017e6ca3a101d7998db.png$

Figura$\PageIndex{2}$: Enfatizando líneas rectas yendo a líneas rectas en Ejemplo$\PageIndex{1}$.

Para enfatizar cómo “las líneas rectas se transforman en líneas rectas”, considere Figura$\PageIndex{2}$. Aquí, el cuadrado unitario tiene algunos puntos adicionales dibujados en él que corresponden a los puntos sombreados en el paralelogramo transformado. Observe cómo también se conservan las distancias relativas; el punto a medio camino entre los puntos negros y cuadrados se transforma a una posición a lo largo de la línea, a medio camino entre los puntos negros y cuadrados.

Mucho más se puede decir sobre este ejemplo. Antes de ahondar en esto, sin embargo, probemos un ejemplo más.

Ejemplo$\PageIndex{2}$

Trazar la unidad cuadrada transformada después de que haya sido transformada por$A$, donde

\[A=\left[\begin{array}{cc}{0}&{-1}\\{1}&{0}\end{array}\right]. \nonumber \]

Solución

Pondremos los vectores que corresponden a cada esquina en una matriz$B$ como antes y luego la multiplicaremos a la izquierda por$A$. Hacerlo da:

\[\begin{align}\begin{aligned}AB&=\left[\begin{array}{cc}{0}&{-1}\\{1}&{0}\end{array}\right]\left[\begin{array}{cccc}{0}&{1}&{1}&{0}\\{0}&{0}&{1}&{1}\end{array}\right] \\ &=\left[\begin{array}{cccc}{0}&{0}&{-1}&{-1}\\{0}&{1}&{1}&{0}\end{array}\right]\end{aligned}\end{align} \nonumber \]

En$\PageIndex{3}$ la Figura se dibuja nuevamente el cuadrado unitario junto con su transformación por$A$.

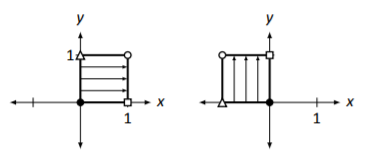
$clipboard_ed312dd7935f512d62a7b13a285c3fa9f.png$

Figura$\PageIndex{3}$: Transformar el cuadrado unitario por multiplicación matricial en Ejemplo$\PageIndex{2}$.

Toma nota de cómo se movió el cuadrado. No se limitó a “deslizarse” hacia la izquierda; $^{2}$ni se “volteó” a través del$y$ eje. Más bien, se giró en sentido antihorario sobre el origen$90^\circ$. En una rotación, la forma de un objeto no cambia; en nuestro ejemplo, el cuadrado quedó un cuadrado del mismo tamaño.

Hemos abordado el tema de cómo se puede transformar el plano cartesiano a través de la multiplicación por una$2\times 2$ matriz$A$. Hemos visto dos ejemplos hasta ahora, y nuestra intuición en cuanto a cómo se cambia el plano se ha informado sólo al ver cómo cambia el cuadrado unitario. Exploremos esto más a fondo investigando dos preguntas:

Supongamos que queremos transformar el plano cartesiano de una manera conocida (por ejemplo, es posible que queramos rotar el plano en sentido antihorario$180^\circ$). ¿Cómo encontramos la matriz (si existe una) que realiza esta transformación?
¿Cómo es que saber cómo se transforma la unidad cuadrada ayuda realmente a entender cómo se transforma todo el plano?

Estas preguntas están estrechamente relacionadas, y a medida que respondamos una, ayudaremos a responder a la otra.

Para comenzar con la primera pregunta, mire hacia atrás en Ejemplos$\PageIndex{1}$$\PageIndex{2}$ y considere nuevamente cómo se transformó el cuadrado unitario. En particular, ¿existe alguna correlación entre dónde terminaron los vértices y la matriz$A$?

Si solo estás leyendo, y en realidad no has vuelto atrás y miraste los ejemplos, vuelve ahora y trata de hacer algún tipo de conexión. De lo contrario, es posible que hayas notado algunas de las siguientes cosas:

El vector cero ($\vec{0}$, la esquina “negra”) nunca se movió. Eso tiene sentido, aunque;$A\vec{0}=\vec{0}$.
La esquina “cuadrada”, es decir, la esquina correspondiente al vector$\left[\begin{array}{c}{1}\\{0}\end{array}\right]$, siempre se transforma en el vector en la primera columna de$A$!
Así mismo, la esquina “triangular”, es decir, la esquina correspondiente al vector$\left[\begin{array}{c}{0}\\{1}\end{array}\right]$, siempre se transforma en el vector en la segunda columna de$A$! $^{3}$
La esquina del “punto blanco” siempre se transforma a la suma de los dos vectores de columna de$A$. $^{4}$

Tomemos ahora el tiempo para entender estos cuatro puntos. El primer punto debe ser claro; siempre$\vec{0}$ se transformará a$\vec{0}$ través de la multiplicación matricial. (De ahí la pista en medio de Ejemplo$\PageIndex{1}$, donde se nos dice que podemos ignorar entrar en la columna de ceros en la matriz$B$.)

Podemos entender el segundo y tercer puntos simultáneamente. Vamos

\[A=\left[\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}\right],\quad\vec{e_{1}}=\left[\begin{array}{c}{1}\\{0}\end{array}\right]\quad\text{and}\quad\vec{e_{2}}=\left[\begin{array}{c}{0}\\{1}\end{array}\right]. \nonumber \]

¿Qué son$A\vec{e_{1}}$ y$A\vec{e_{2}}$?

\[\begin{align}\begin{aligned}A\vec{e_{1}}&=\left[\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}\right]\left[\begin{array}{c}{1}\\{0}\end{array}\right] \\ &=\left[\begin{array}{c}{a}\\{c}\end{array}\right]\end{aligned}\end{align} \nonumber \]

\[\begin{align}\begin{aligned}A\vec{e_{2}}&=\left[\begin{array}{cc}{a}&{b}\\{c}&{d}\end{array}\right]\left[\begin{array}{c}{0}\\{1}\end{array}\right] \\ &=\left[\begin{array}{c}{b}\\{d}\end{array}\right]\end{aligned}\end{align} \nonumber \]

Entonces, por mera mecánica de multiplicación matricial, la esquina cuadrada$\vec{e_{1}}$ se transforma en la primera columna de$A$, y la esquina triangular$\vec{e_{2}}$ se transforma en la segunda columna de$A$. Un argumento similar demuestra por qué la esquina del punto blanco se transforma en la suma de las columnas de$A$. $^{5}$

Vuelva a visitar ahora la pregunta “¿Cómo encontramos la matriz que realiza una transformación dada en el plano cartesiano?” La respuesta se desprende de lo que acabamos de hacer. Piense en la transformación dada y cómo transformaría las esquinas de la unidad cuadrada. Hacer la primera columna$A$ del vector donde$\vec{e_{1}}$ va, y hacer la segunda columna$A$ del vector donde$\vec{e_{2}}$ va.

Practicemos esto en el contexto de un ejemplo.

Ejemplo$\PageIndex{3}$

Encuentra la matriz$A$ que voltea el plano cartesiano alrededor del$x$ eje y luego estira el plano horizontalmente por un factor de dos.

Solución

Primero consideramos$\vec{e_{1}}=\left[\begin{array}{c}{1}\\{0}\end{array}\right]$. ¿A dónde va este rincón bajo la transformación dada? Voltear el plano a través del$x$ eje no cambia$\vec{e_{1}}$ en absoluto; estirar el plano envía$\vec{e_{1}}$ a$\left[\begin{array}{c}{2}\\{0}\end{array}\right]$. Por lo tanto, la primera columna de$A$ es$\left[\begin{array}{c}{2}\\{0}\end{array}\right]$.

Ahora considere$\vec{e_{2}}=\left[\begin{array}{c}{0}\\{1}\end{array}\right]$. Voltear el plano alrededor del$x$ eje se envía$\vec{e_{2}}$ al vector$\left[\begin{array}{c}{0}\\{-1}\end{array}\right]$; posteriormente estirar el plano horizontalmente no afecta a este vector. Por lo tanto la segunda columna de$A$ es$\left[\begin{array}{c}{0}\\{-1}\end{array}\right]$.

Armando esto da

\[A=\left[\begin{array}{cc}{2}&{0}\\{0}&{-1}\end{array}\right]. \nonumber \]

Para ayudar a visualizar esto, considere Figura$\PageIndex{4}$ donde una forma se transforma bajo esta matriz. Observe cómo se pone boca abajo y se estira horizontalmente por un factor de dos. (Las líneas de la cuadrícula se dan como ayuda visual).

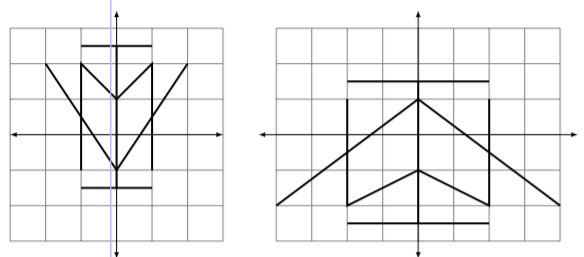
$clipboard_e5e0b2bb8579f849df2d123963ef15990.png$

Figura$\PageIndex{4}$: Transformando el plano cartesiano en Ejemplo$\PageIndex{3}$.

Hace un tiempo hicimos dos preguntas. El primero fue “¿Cómo encontramos la matriz que realiza una transformación dada?” Acabamos de responder a esa pregunta (aunque haremos más para explorarla en el futuro). La segunda pregunta fue “¿Cómo es que saber cómo se transforma realmente la unidad cuadrada nos ayuda a entender cómo se transforma todo el plano?”

Considere Figura$\PageIndex{5}$ donde se muestra el cuadrado unitario (con vértices marcados con formas como antes) transformado bajo una matriz desconocida. ¿Cómo nos ayuda esto a entender cómo se transforma todo el plano cartesiano? Por ejemplo, ¿cómo podemos usar esta imagen para averiguar cómo se$(2,3)$ transformará el punto?

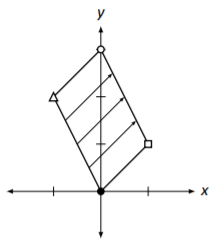
$clipboard_ed369caec0be23384c1b5a441677bd4b2.png$

Figura$\PageIndex{5}$: El cuadrado unitario bajo una transformación desconocida.

Hay dos formas de considerar la solución a esta cuestión. Primero, ahora sabemos cómo calcular la matriz de transformación; la nueva posición de$\vec{e_{1}}$ es la primera columna de$A$, y la nueva posición de$\vec{e_{2}}$ es la segunda columna de$A$. Por lo tanto, al mirar la figura, podemos deducir que $^{6}$

\[A=\left[\begin{array}{cc}{1}&{-1}\\{1}&{2}\end{array}\right]. \nonumber \]

Para encontrar dónde$(2,3)$ se envía el punto, simplemente multiplique

\[\left[\begin{array}{cc}{1}&{-1}\\{1}&{2}\end{array}\right]\left[\begin{array}{c}{2}\\{3}\end{array}\right]=\left[\begin{array}{c}{-1}\\{8}\end{array}\right]. \nonumber \]

Hay otra forma de hacer esto que no es tan computacional, no implica computar la matriz de transformación. Considera las siguientes igualdades:

\[\begin{align}\begin{aligned}\left[\begin{array}{c}{2}\\{3}\end{array}\right]&=\left[\begin{array}{c}{2}\\{0}\end{array}\right]+\left[\begin{array}{c}{0}\\{3}\end{array}\right] \\ &=2\left[\begin{array}{c}{1}\\{0}\end{array}\right] +3\left[\begin{array}{c}{0}\\{1}\end{array}\right] \\ &=2\vec{e_{1}}+3\vec{e_{2}}\end{aligned}\end{align} \nonumber \]

Esta última igualdad afirma algo que es algo obvio: para llegar al vector$\left[\begin{array}{c}{2}\\{3}\end{array}\right]$, hay que ir$2$ unidades en la$\vec{e_{1}}$ dirección y$3$ unidades en la$\vec{e_{2}}$ dirección. Para encontrar dónde$(2,3)$ se transforma el punto, hay que ir$2$ unidades en la nueva$\vec{e_{1}}$ dirección y$3$ unidades en la nueva$\vec{e_{2}}$ dirección. Esto se demuestra en la Figura$\PageIndex{6}$.

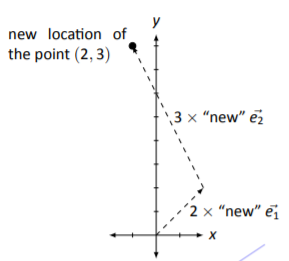
$clipboard_eb692aa98eef5c0a0a87b43e7ca82ee9a.png$

Figura$\PageIndex{6}$: Encontrar la nueva ubicación del punto$(2,3)$.

Estamos llegando a entender cómo funcionan las transformaciones matriciales. Hicimos dos preguntas básicas: “¿Cómo encontramos la matriz para una transformación dada?” y “¿Cómo entendemos la transformación sin la matriz?” , y hemos respondido a cada uno acompañado de un ejemplo. Hagamos otro ejemplo que demuestre ambas técnicas a la vez.

Ejemplo$\PageIndex{4}$

Primero, encuentra la matriz$A$ que transforma el plano cartesiano estirándolo verticalmente por un factor de$1.5$, luego lo estira horizontalmente por un factor de$0.5$, luego lo gira en sentido horario alrededor del origen$90^{\circ}$. En segundo lugar, utilizando las nuevas ubicaciones de$\vec{e_{1}}$ y$\vec{e_{2}}$, encontrar la ubicación transformada del punto$(−1, 2)$.

Solución

Para encontrar$A$, primero considere la nueva ubicación de$\vec{e_{1}}$. Estirar el plano verticalmente no afecta$\vec{e_{1}}$; estirar el plano horizontalmente por un factor de$0.5$ cambios$\vec{e_{1}}$ a$\left[\begin{array}{c}{1/2}\\{0}\end{array}\right]$, y luego girarlo$90^\circ$ alrededor del origen lo mueve hacia$\left[\begin{array}{c}{0}\\{-1/2}\end{array}\right]$. Esta es la primera columna de$A$.

Ahora considere la nueva ubicación de$\vec{e_{2}}$. Estirar el plano verticalmente lo cambia a$\left[\begin{array}{c}{0}\\{3/2}\end{array}\right]$; estirarlo horizontalmente no lo afecta, y girar lo$90^\circ$ mueve hacia$\left[\begin{array}{c}{3/2}\\{0}\end{array}\right]$. Esta es entonces la segunda columna de$A$. Esto da

\[A=\left[\begin{array}{cc}{0}&{3/2}\\{-1/2}&{0}\end{array}\right]. \nonumber \]

¿A dónde se envía el punto$(-1,2)$? El vector correspondiente$\left[\begin{array}{c}{-1}\\{2}\end{array}\right]$ se encuentra yendo$-1$ unidades en la$\vec{e_{1}}$ dirección y$2$ unidades en la$\vec{e_{2}}$ dirección. Por lo tanto, la transformación enviará el vector a$-1$ unidades en la nueva$\vec{e_{1}}$ dirección y$2$ unidades en la nueva$\vec{e_{2}}$ dirección. Esto se esboza en la Figura$\PageIndex{7}$, junto con el cuadrado unitario transformado. También podemos comprobar esto multiplicativamente:

\[\left[\begin{array}{cc}{0}&{3/2}\\{-1/2}&{0}\end{array}\right]\left[\begin{array}{c}{-1}\\{2}\end{array}\right]=\left[\begin{array}{c}{3}\\{1/2}\end{array}\right]. \nonumber \]

La figura$\PageIndex{8}$ muestra los efectos de la transformación en otra forma.

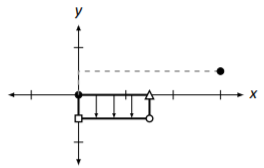
$clipboard_e301aac0f1bc051d646c4502ef742b9e3.png$

Figura$\PageIndex{7}$: Entendiendo la transformación en Ejemplo$\PageIndex{4}$.

$clipboard_e47c2f051910b3740b023d4c1b6388f2f.png$

Figura$\PageIndex{8}$: Transformando el plano cartesiano en Ejemplo$\PageIndex{4}$.

Ahora mismo nos estamos enfocando en transformar el plano cartesiano — estamos haciendo transformaciones 2D. Saber cómo hacer esto proporciona una base para transformar el espacio 3D, $^{7}$lo cual, entre otras cosas, es muy importante a la hora de producir gráficos por computadora 3D. Las formas básicas se pueden dibujar y luego rotar, estirar y/o mover a otras regiones del espacio. Esto también permite cosas como “mover la vista de la cámara”.

¿Qué tipo de transformaciones son posibles? Ya hemos visto algunas de las cosas que son posibles: rotaciones, estiramientos y volteretas. También hemos mencionado algunas cosas que no son posibles. Por ejemplo, afirmamos que las líneas rectas siempre se transforman en rectas. Por lo tanto, no podemos transformar el cuadrado unitario en un círculo usando una matriz.

Veamos algunas transformaciones comunes del plano cartesiano y las matrices que realizan estas operaciones. En las siguientes figuras, se dará una matriz de transformación junto con una imagen del cuadrado unitario transformado. (El cuadrado unitario original también se dibuja ligeramente para servir como referencia).

Transformaciones de Matriz 2D

Estiramiento horizontal por un factor de$k$.

\[\left[\begin{array}{cc}{k}&{0}\\{0}&{1}\end{array}\right]\nonumber \]

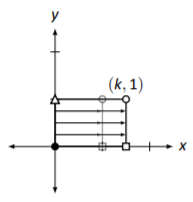$clipboard_ed9ab4c9ad25a6366ef0d300ab175bf94.png$

Estiramiento vertical por un factor de$k$.

\[\left[\begin{array}{cc}{1}&{0}\\{0}&{k}\end{array}\right]\nonumber \]

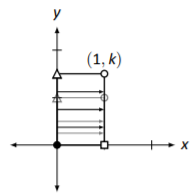$clipboard_edc6a947e626924b2d0cac3d0ab59f523.png$

Cizalla horizontal por un factor de$k$.

\[\left[\begin{array}{cc}{1}&{k}\\{0}&{1}\end{array}\right]\nonumber \]

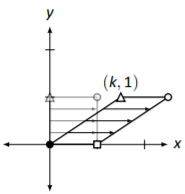$clipboard_eb6abfdce07bb93f3817f7d412dcf98e5.png$

Cizalla vertical por un factor de$k$.

\[\left[\begin{array}{cc}{1}&{0}\\{k}&{1}\end{array}\right]\nonumber \]

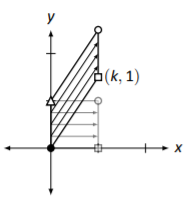$clipboard_ef603a700420a3cc4e10a45ec239e3835.png$

Reflexión horizontal a través del$y$ eje

\[\left[\begin{array}{cc}{-1}&{0}\\{0}&{1}\end{array}\right]\nonumber \]

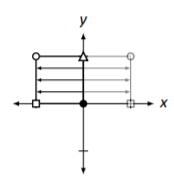$clipboard_e7cd824a8abea122d523f2c4c1adc32f2.png$

Reflexión vertical a través del$x$ eje.

\[\left[\begin{array}{cc}{1}&{0}\\{0}&{-1}\end{array}\right]\nonumber \]

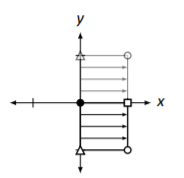$clipboard_e437a8776f2c2dd42deca9cb391706469.png$

Reflexión diagonal a través de la línea$y=x$.

\[\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right]\nonumber \]

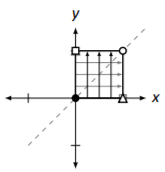$clipboard_e42478112c5b6409e2e67b5d2e0cd37b1.png$

Rotación alrededor del origen por un ángulo de$\theta$.

\[\left[\begin{array}{cc}{\cos\theta}&{-\sin\theta} \\ {\sin\theta}&{\cos\theta}\end{array}\right]\nonumber \]

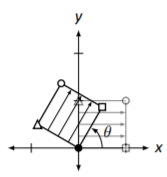$clipboard_e32cae881e4b87cdc2cf1c4a8b563cb0f.png$

Proyección sobre el$x$ eje.

(Observe cómo el cuadrado está “aplastado” en el$x$ eje -axis.)

\[\left[\begin{array}{cc}{1}&{0}\\{0}&{0}\end{array}\right]\nonumber \]

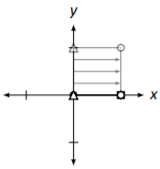$clipboard_e230040d2ea452eb7319ff946848d45bd.png$

Proyección sobre el$y$ eje.

(Observe cómo el cuadrado está “aplastado” sobre el$y$ eje -axis.)

\[\left[\begin{array}{cc}{0}&{0}\\{0}&{1}\end{array}\right]\nonumber \]

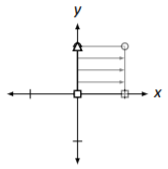$clipboard_e406f2c30ebb0cf4924a77a2f2ece8fa8.png$

Ahora que hemos visto una lista saludable de transformaciones que podemos realizar en el plano cartesiano, practiquemos algunas veces más creando la matriz que da la transformación deseada. En el siguiente ejemplo, desarrollamos nuestro entendimiento un paso más crítico.

Ejemplo$\PageIndex{5}$

Encuentra la matriz$A$ que transforma el plano cartesiano realizando las siguientes operaciones en orden:

Cizalla vertical por un factor de$0.5$
Roation en sentido antihorario sobre el origen por un ángulo de$\theta=30^{\circ}$
Estiramiento horizontal por un factor de$2$
Reflexión diagonal a través de la línea$y=x$

Solución

¡Guau! Ya sabemos cómo hacer esto —algo así como. Sabemos que podemos encontrar las columnas de$A$ trazando dónde$\vec{e_{1}}$ y$\vec{e_{2}}$ terminar, pero esto también parece difícil. Hay tanto que está pasando. Afortunadamente, podemos lograr lo que necesitamos sin mucha dificultad siendo sistemáticos.

Primero, vamos a realizar la cizalla vertical. La matriz que realiza esto es

\[A_{1}=\left[\begin{array}{cc}{1}&{0}\\{0.5}&{1}\end{array}\right]. \nonumber \]

Después de eso, queremos rotar todo en sentido horario por$30^\circ$. Para ello, utilizamos

\[A_{2}=\left[\begin{array}{cc}{\cos 30^{\circ}}&{-\sin 30^{\circ}} \\ {\sin 30^{\circ}}&{\cos 30^{\circ}}\end{array}\right] =\left[\begin{array}{cc}{\sqrt{3}/2}&{-1/2}\\{1/2}&{\sqrt{3}/2}\end{array}\right]. \nonumber \]

Para hacer ambas operaciones, en orden, multiplicamos$A_{2}A_{1}$.$^{8}$

Para realizar las dos últimas operaciones, observamos que

\[A_{3}=\left[\begin{array}{cc}{2}&{0}\\{0}&{1}\end{array}\right]\quad\text{\and}\quad A_{4}= \left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right] \nonumber \]

realizar el estiramiento horizontal y la reflexión diagonal, respectivamente. Así, para realizar todas las operaciones “a la vez”, necesitamos multiplicar por

\[\begin{align}\begin{aligned}A&=A_{4}A_{3}A_{2}A_{1} \\ &=\left[\begin{array}{cc}{0}&{1}\\{1}&{0}\end{array}\right]\left[\begin{array}{cc}{2}&{0}\\{0}&{1}\end{array}\right]\left[\begin{array}{cc}{\sqrt{3}/2}&{-1/2} \\ {1/2}&{\sqrt{3}/2}\end{array}\right]\left[\begin{array}{cc}{1}&{0}\\{0.5}&{1}\end{array}\right] \\ &=\left[\begin{array}{cc}{(\sqrt{3}+2)/4}&{\sqrt{3}/2} \\ {(2\sqrt{3}-1)/2}&{-1}\end{array}\right] \\ &\approx\left[\begin{array}{cc}{0.933}&{0.866} \\ {1.232}&{-1}\end{array}\right].\end{aligned}\end{align} \nonumber \]

Consideremos esto de cerca. Supongamos que quiero saber dónde$\vec{x}$ termina un vector. Afirmamos que podemos encontrar la respuesta multiplicando$A\vec{x}$. ¿Por qué funciona esto? Considerar:

\[\begin{align}\begin{aligned}A\vec{x}&=A_{4}A_{3}A_{2}A_{1}\vec{x} \\ &=A_{4}A_{3}A_{2}(A_{1}\vec{x}) &\text{(performs the vertical shear)} \\ &=A_{4}A_{3}(A_{2}\vec{x_{1}}) &\text{(performs the rotation)} \\ &=A_{4}(A_{3}\vec{x_{2}}) &\text{(performs the horizontal stretch)} \\ &=A_{4}\vec{x_{3}} &\text{(performs the diagonal reflection)} \\ &=\vec{x_{4}} &\text{(the result of transforming }\vec{x}\text{)}\end{aligned}\end{align} \nonumber \]

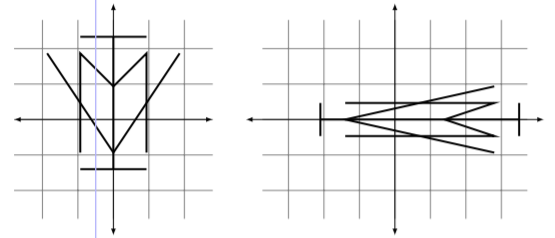
La mayoría de los lectores no son capaces de visualizar exactamente lo que la lista dada de operaciones le hace al plano cartesiano. En Figura$\PageIndex{9}$ esbozamos el cuadrado unitario transformado; en Figura$\PageIndex{10}$ esbozamos una forma y su transformación.

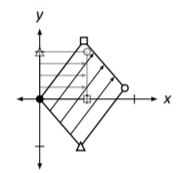
$clipboard_e8b80ae527996806fe9fcaae8bbfa521e.png$

Figura$\PageIndex{9}$: El cuadrado unitario transformado en Ejemplo$\PageIndex{5}$.

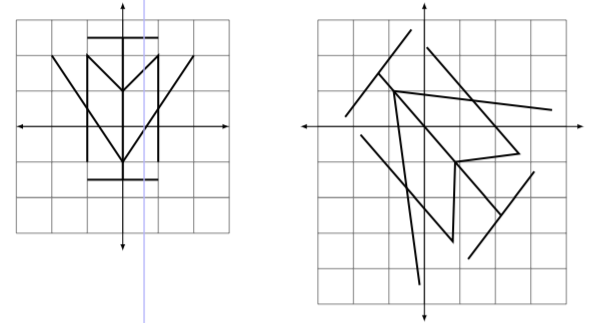
$clipboard_e0e9b602ea6619536720981e170ad2e2e.png$

Figura$\PageIndex{10}$: Una forma transformada en Ejemplo$\PageIndex{5}$.

Una vez que sabemos qué matrices realizan las transformaciones básicas, $^{9}$realizar transformaciones complejas en el plano cartesiano realmente no es tan$\ldots$ complejo. Se reduce a multiplicar por una serie de matrices.

Hemos mostrado muchos ejemplos de transformaciones que podemos hacer, y hemos mencionado solo algunos que no podemos —por ejemplo, no podemos convertir un cuadrado en un círculo. ¿Por qué no? ¿Por qué es que las líneas rectas se envían a líneas rectas? Pasamos mucho tiempo dentro de este texto mirando matrices invertibles; ¿qué conexiones, si las hay, $^{10}$hay entre las matrices invertibles y sus transformaciones en el plano cartesiano?

Todas estas preguntas requieren que pensemos como matemáticos —se nos está pidiendo que estudiemos las propiedades de un objeto del que acabamos de aprender y sus conexiones con cosas que ya hemos aprendido. Haremos todo esto (¡y más!) en la siguiente sección.

Notas al pie

[1] No, no los haremos uno por uno.

[2] matemáticamente, eso se llama traducción

[3] Aunque esto es menos sorpresa, dado el resultado del punto anterior.

[4] Esta observación es un poco más oscura que las tres primeras. De ello se desprende que esta esquina del cuadrado unitario es la “suma” de las otras dos esquinas distintas de cero.

[5] Otra forma de ver todo esto es considerar lo que$A\cdot I$ es: claro, es justo$A$. ¿De qué son las columnas$I$? Justo$\vec{e_{1}}$ y$\vec{e_{2}}$.

[6] Al menos,$A$ está cerca de eso. La esquina cuadrada en realidad podría estar en el punto$(1.01, .99)$.

[7] En realidad, proporciona una base para hacerlo en 4D, 5D,$\ldots$, 17D, etc. Esos son simplemente más difíciles de visualizar.

[8] El lector podría preguntar: “¿Es importante hacer multiplicar estos en ese orden? ¿Podríamos haber multiplicado$A_{1}A_{2}$ en su lugar?” Nuestra respuesta comienza con “¿La multiplicación matricial es conmutativa?” La respuesta a nuestra pregunta es “No”, por lo que las respuestas a las preguntas del lector son “Sí” y “No”, respectivamente.

[9] o saber dónde encontrarlos

[10] A estas alturas, el lector debería esperar que existan conexiones.

Search

Ejemplo\(\PageIndex{5}\)

Objetivos de aprendizaje

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)

Ejemplo\(\PageIndex{4}\)

Transformaciones de Matriz 2D

Ejemplo\(\PageIndex{5}\)

Notas al pie