5.1.1: Ejercicios 5.1

Última actualización
Guardar como PDF

Page ID: 116549

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En Ejercicios$\PageIndex{1}$ -$\PageIndex{4}$, se da un boceto del cuadrado unitario transformado. Encuentra la matriz$A$ que realiza esta transformación.

Ejercicio$\PageIndex{1}$

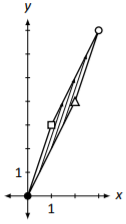
$clipboard_e2895a3158a3263c1c6bbb7b29f87703b.png$

Contestar: $A=\left[\begin{array}{cc}{1}&{2}\\{3}&{4}\end{array}\right]$

Ejercicio$\PageIndex{2}$

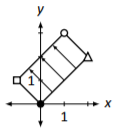
$clipboard_e9a13b70e3e27d7531429f3dae7fdf330.png$

Contestar: $A=\left[\begin{array}{cc}{-1}&{2}\\{1}&{2}\end{array}\right]$

Ejercicio$\PageIndex{3}$

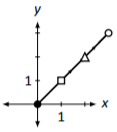
$clipboard_ee821ea81eef56e37593704bd0d24854a.png$

Contestar: $A=\left[\begin{array}{cc}{1}&{2}\\{1}&{2}\end{array}\right]$

Ejercicio$\PageIndex{4}$

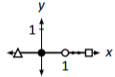
$clipboard_e434bf5cdd4a31c6b5671db2de6967e2d.png$

Contestar: $A=\left[\begin{array}{cc}{2}&{-1}\\{0}&{0}\end{array}\right]$

En Ejercicios$\PageIndex{5}$ —$\PageIndex{10}$, se da una lista de transformaciones. Encuentra la matriz$A$ que realiza esas transformaciones, en orden, en el plano cartesiano.

Ejercicio$\PageIndex{5}$

cizallamiento vertical por un factor de$2$
cizallamiento horizontal por un factor de$2$

Contestar: $A=\left[\begin{array}{cc}{5}&{2}\\{2}&{1}\end{array}\right]$

Ejercicio$\PageIndex{6}$

cizallamiento horizontal por un factor de$2$
cizallamiento vertical por un factor de$2$

Contestar: $A=\left[\begin{array}{cc}{1}&{2}\\{2}&{5}\end{array}\right]$

Ejercicio$\PageIndex{7}$

estiramiento horizontal por un factor de$3$
reflexión a través de la línea$y = x$

Contestar: $A=\left[\begin{array}{cc}{0}&{1}\\{3}&{0}\end{array}\right]$

Ejercicio$\PageIndex{8}$

rotación en sentido antihorario por un ángulo de$45^{\circ}$
estiramiento vertical por un factor de$1/2$

Contestar: $A=\left[\begin{array}{cc}{0.707}&{-0.707}\\{0.354}&{0.354}\end{array}\right]$

Ejercicio$\PageIndex{9}$

rotación en sentido horario por un ángulo de$90^{\circ}$
reflexión horizontal a través del$y$ eje
cizallamiento vertical por un factor de$1$

Contestar: $A=\left[\begin{array}{cc}{0}&{-1}\\{-1}&{-1}\end{array}\right]$

Ejercicio$\PageIndex{10}$

reflexión vertical a través del$x$ eje
reflexión horizontal a través del$y$ eje
reflexión diagonal a través de la línea$y = x$

Contestar: $A=\left[\begin{array}{cc}{0}&{-1}\\{-1}&{0}\end{array}\right]$

En Ejercicios$\PageIndex{11}$ —$\PageIndex{14}$, se dan dos conjuntos de transformaciones. Esboce el cuadrado unitario transformado debajo de cada conjunto de transformaciones. ¿Las transformaciones son las mismas? Explica por qué/ por qué no.

Ejercicio$\PageIndex{11}$

una reflexión horizontal a través del$y$ eje, seguida de una reflexión vertical a través del$x$ eje, en comparación con
una rotación en sentido antihorario de$180^{\circ}$

Contestar: Sí, estos son los mismos; la matriz de transformación en cada uno es$\left[\begin{array}{cc}{-1}&{0}\\{0}&{-1}\end{array}\right]$.

Ejercicio$\PageIndex{12}$

un estiramiento horizontal por un factor de$2$ seguido de una reflexión a través de la línea$y = x$, en comparación con
un estiramiento vertical por un factor de$2$

Contestar: No, estos son diferentes. El primero produce una matriz de transformación$\left[\begin{array}{cc}{0}&{1}\\{2}&{0}\end{array}\right]$, que el segundo produce$\left[\begin{array}{cc}{1}&{0}\\{0}&{2}\end{array}\right]$.

Ejercicio$\PageIndex{13}$

un estiramiento horizontal por un factor de$1/2$ seguido de un estiramiento vertical por un factor de$3$, comparado con
las mismas operaciones pero en orden opuesto

Contestar: Sí, estos son los mismos. Cada uno produce la matriz de transformación$\left[\begin{array}{cc}{1/2}&{0}\\{0}&{3}\end{array}\right]$.

Ejercicio$\PageIndex{14}$

una reflexión a través de la línea$y = x$ seguida de una reflexión a través del$x$ eje, en comparación con
una reflexión a través del$y$ eje, seguida de una reflexión a través de la línea$y = x$.

Contestar: Sí, estos son los mismos. Cada uno produce la matriz de transformación$\left[\begin{array}{cc}{0}&{1}\\{-1}&{0}\end{array}\right]$.

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)