5.E: Ejercicios

Ejercicio\(\PageIndex{1}\)

Mostrar el mapa\(T\):\(\mathbb{R}^n → \mathbb{R}^m\) definido por\(T (\vec{x}) = A\vec{x}\) donde\(A\) es una\(m\times n\) matriz y\(\vec{x}\) es un vector de\(m\times 1\) columna es una transformación lineal.

Contestar

Este resultado se desprende de las propiedades de la multiplicación matricial.

Ejercicio\(\PageIndex{2}\)

Mostrar que la función\(T_{\vec{u}}\) definida por\(T_{\vec{u}} (\vec{v}) =\vec{v}−proj_{\vec{u}} (\vec{v})\) es también una transformación lineal.

Contestar

\[\begin{aligned}T_{\vec{u}}(a\vec{v}+b\vec{w})&=a\vec{v}+b\vec{w}-\frac{(a\vec{v}+b\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=a\vec{v}-a\frac{(\vec{v}\bullet\vec{u})}{||\vec{u}||^2}\vec{u}+b\vec{w}-b\frac{(\vec{w}\bullet\vec{u})}{||\vec{u}||^2}\vec{u} \\ &=aT_{\vec{u}}(\vec{v})+bT_{\vec{u}}(\vec{w})\end{aligned}\]

Ejercicio\(\PageIndex{3}\)

Dejar\(\vec{u}\) ser un vector fijo. La función\(T_{\vec{u}}\) definida por\(T_{\vec{u}}\vec{v} =\vec{u}+\vec{v}\) tiene el efecto de traducir todos los vectores sumando\(\vec{u}\neq\vec{0}\). Mostrar que esto no es una transformación lineal. Explique por qué no es posible representar\(T_{\vec{u}}\) en\(\mathbb{R}^3\) multiplicando por una\(3×3\) matriz.

Contestar

Transformaciones lineales llevan\(\vec{0}\) a\(\vec{0}\) lo que\(T\) no. También\(T_{\vec{a}} (\vec{u}+\vec{v})\neq T_{\vec{a}}\vec{u}+T_{\vec{a}}\vec{v}\).

Ejercicio\(\PageIndex{4}\)

Considera las siguientes funciones que mapean\(\mathbb{R}^n\) a\(\mathbb{R}^n\).

1. \(T\)multiplica el componente\(j\) th de\(\vec{x}\) por un número distinto de cero\(b\).
2. \(T\)reemplaza el componente\(i\) th\(\vec{x}\) de\(b\) por veces el componente\(j\) th agregado al componente\(i\) th.
3. \(T\)cambia los componentes\(i\) th y\(j\) th.

Mostrar estas funciones son transformaciones lineales y describir sus matrices de\(A\) tal manera que\(T (\vec{x}) = A\vec{x}\).

Contestar

1. La matriz de\(T\) es la matriz elemental que multiplica la entrada diagonal\(j\) th de la matriz de identidad por\(b\).
2. La matriz de\(T\) es la matriz elemental que toma\(b\) veces la fila\(j\) th y se suma a la fila\(i\) th.
3. La matriz de\(T\) es la matriz elemental que cambia las filas\(i\) th y\(j\) th donde los dos componentes están en las posiciones\(i\) th y\(j\) th.

Ejercicio\(\PageIndex{5}\)

Se te da una transformación lineal\(T\):\(\mathbb{R}^n → \mathbb{R}^m\) y sabes que\[T(A_i)=B_i\nonumber\] donde\([A_1\cdots a_n]^{-1}\) existe. Demostrar que la matriz de\(T\) es de la forma\[[B_1\cdots B_n][A_1\cdots A_n]^{-1}\nonumber\]

Contestar

Supongamos\[\left[\begin{array}{c}\vec{c}_1^{T} \\ \vdots \\ \vec{c}_n^T \end{array}\right]=\left[\begin{array}{ccc}\vec{a}_1&\cdots &\vec{a}_n\end{array}\right]^{-1}\nonumber\] Así\(\vec{c}_i^T\vec{a}_j=\delta_{ij}\). Por lo\[\begin{aligned} \left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i&=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{c}\vec{c}_1^T \\ \vdots \\ \vec{c}_n^T\end{array}\right]\vec{a}_i\\ &=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\vec{e}_i \\ &=\vec{b}_i\end{aligned}\] tanto, así\(T\vec{a}_i=\left[\begin{array}{ccc}\vec{b}_1&\cdots&\vec{b}_n\end{array}\right]\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]^{-1}\vec{a}_i=A\vec{a}_i\). Si\(\vec{x}\) es arbitrario, entonces como la matriz\(\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\) es invertible, existe una única\(\vec{y}\) tal que\(\left[\begin{array}{ccc}\vec{a}_1&\cdots&\vec{a}_n\end{array}\right]\vec{y}=\vec{x}\) De ahí\[T\vec{x}=T\left(\sum\limits_{i=1}^n y_i\vec{a}_i\right)=\sum\limits_{i=1}^n y_iT\vec{a}_i=\sum\limits_{i=1}^n y_iA\vec{a}_i=A\left(\sum\limits_{i=1}^ny_i\vec{a}_i\right)=A\vec{x}\nonumber\]

Ejercicio\(\PageIndex{6}\)

Supongamos que\(T\) es una transformación lineal tal que\[\begin{aligned}T\left[\begin{array}{r}1\\2\\-6\end{array}\right]&=\left[\begin{array}{r}5\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\5\end{array}\right]&=\left[\begin{array}{r}1\\1\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-2\end{array}\right]\end{aligned}\] Encuentra la matriz de\(T\). Eso es encontrar\(A\) tal que\(T(\vec{x}) = A\vec{x}\).

Contestar

\[\left[\begin{array}{ccc}5&1&5\\1&1&3\\3&5&-2\end{array}\right]\left[\begin{array}{ccc}3&2&1\\2&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}37&17&11 \\ 17&7&5\\11&14&6\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{7}\)

Supongamos que\(T\) es una transformación lineal tal que\[\begin{aligned}T\left[\begin{array}{r}1\\1\\-8\end{array}\right]&=\left[\begin{array}{r}1\\3\\1\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}2\\4\\1\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\3\end{array}\right]&=\left[\begin{array}{r}6\\1\\-1\end{array}\right]\end{aligned}\] Encuentra la matriz de\(T\). Eso es encontrar\(A\) tal que\(T(\vec{x})=A\vec{x}\).

Contestar

\[\left[\begin{array}{ccc}1&2&6\\3&4&1\\1&1&-1\end{array}\right]\left[\begin{array}{ccc}6&3&1\\5&3&1\\6&2&1\end{array}\right]=\left[\begin{array}{ccc}52&21&9\\44&23&8\\5&4&1\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{8}\)

Supongamos que\(T\) es una transformación lineal tal que\[\begin{aligned}T\left[\begin{array}{r}1\\3\\-7\end{array}\right]&=\left[\begin{array}{r}-3\\1\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\-2\\6\end{array}\right]&=\left[\begin{array}{r}1\\3\\-3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}5\\3\\-3\end{array}\right]\end{aligned}\] Encuentra la matriz de\(T\). Eso es encontrar\(A\) tal que\(T(\vec{x})=A\vec{x}\).

Contestar

\[\left[\begin{array}{ccc}-3&1&5\\1&3&3\\3&-3&-3\end{array}\right]\left[\begin{array}{ccc}2&2&1\\1&2&1\\4&1&1\end{array}\right]=\left[\begin{array}{ccc}15&1&3\\17&11&7\\-9&-3&-3\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{9}\)

Supongamos que\(T\) es una transformación lineal tal que\[\begin{aligned}T\left[\begin{array}{r}1\\1\\-7\end{array}\right]&=\left[\begin{array}{r}3\\3\\3\end{array}\right] \\ T\left[\begin{array}{r}-1\\0\\6\end{array}\right]&=\left[\begin{array}{r}1\\2\\3\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\2\end{array}\right]&=\left[\begin{array}{r}1\\3\\-1\end{array}\right]\end{aligned}\] Encuentra la matriz de\(T\). Eso es encontrar\(A\) tal que\(T(\vec{x})=A\vec{x}\).

Contestar

\[\left[\begin{array}{ccc}3&1&1\\3&2&3\\3&3&-1\end{array}\right]\left[\begin{array}{ccc}6&2&1\\5&2&1\\6&1&1\end{array}\right]=\left[\begin{array}{ccc}29&9&5\\46&13&8\\27&11&5\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{10}\)

Supongamos que\(T\) es una transformación lineal tal que\[\begin{aligned}T\left[\begin{array}{r}1\\2\\-18\end{array}\right]&=\left[\begin{array}{r}5\\2\\5\end{array}\right] \\ T\left[\begin{array}{r}-1\\-1\\15\end{array}\right]&=\left[\begin{array}{r}3\\3\\5\end{array}\right] \\ T\left[\begin{array}{r}0\\-1\\4\end{array}\right]&=\left[\begin{array}{r}2\\5\\-2\end{array}\right]\end{aligned}\] Encuentra la matriz de\(T\). Eso es encontrar\(A\) tal que\(T(\vec{x})=A\vec{x}\).

Contestar

\[\left[\begin{array}{ccc}5&3&2\\2&3&5\\5&5&-2\end{array}\right]\left[\begin{array}{ccc}11&4&1\\10&4&1\\12&3&1\end{array}\right]=\left[\begin{array}{ccc}109&38&10\\112&35&10\\81&34&8\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{11}\)

Considera las siguientes funciones\(T : \mathbb{R}^3 → \mathbb{R}^2\). Demostrar que cada uno es una transformación lineal y determinar para cada uno la matriz\(A\) tal que\(T(\vec{x}) = A\vec{x}\).

1. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y-3x+z\end{array}\right]\)
2. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}7x+2y+z \\ 3x-11y+2z\end{array}\right]\)
3. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}3x+2y+z \\ x+2y+6z\end{array}\right]\)
4. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}2y-5x+z \\ x+y+z\end{array}\right]\)

Ejercicio\(\PageIndex{12}\)

Considera las siguientes funciones\(T : \mathbb{R}^3 → \mathbb{R}^2\). Explique por qué cada una de estas funciones no\(T\) es lineal.

1. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z+1 \\ 2y-3x+z\end{array}\right]\)
2. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y^2+3z \\ 2y+3x+z\end{array}\right]\)
3. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}\sin x+2y+3z \\ 2y+3x+z\end{array}\right]\)
4. \(T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}x+2y+3z \\ 2y+3x-\ln z\end{array}\right]\)

Ejercicio\(\PageIndex{13}\)

Supongamos que\[ [A_1\cdots A_n]^{-1}\nonumber\] existe donde cada uno\(A_j ∈ \mathbb{R}^n\) y dejar vectores\(\{B_1,\cdots ,B_n\}\) en\(\mathbb{R}^m\) ser dados. Demostrar que siempre existe una transformación lineal\(T\) tal que\(T(A_i) = B_i\).

Ejercicio\(\PageIndex{14}\)

Encuentra la matriz para\(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) dónde\(\vec{v}=\left[\begin{array}{ccc}1&-2&3\end{array}\right]^T\).

Contestar

Recordemos que\(proj_{\vec{u}}(\vec{v})=\frac{\vec{v}\bullet\vec{u}}{||\vec{u}||^2}\vec{u}\) y así la matriz deseada tiene\(i\) th columna igual a\(proj_{\vec{u}}(\vec{e}_i)\). Por lo tanto, la matriz deseada es\[\frac{1}{14}\left[\begin{array}{ccc}1&-2&3\\-2&4&-6\\3&-6&9\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{15}\)

Encuentra la matriz para\(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) dónde\(\vec{v}=\left[\begin{array}{ccc}1&5&3\end{array}\right]^T\).

Contestar

\[\frac{1}{35}\left[\begin{array}{ccc}1&5&3\\5&25&15\\3&15&9\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{16}\)

Encuentra la matriz para\(T (\vec{w}) = proj_{\vec{v}}(\vec{w})\) dónde\(\vec{v}=\left[\begin{array}{ccc}1&0&3\end{array}\right]^T\).

Contestar

\[\frac{1}{10}\left[\begin{array}{ccc}1&0&3\\0&0&0\\3&0&9\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{17}\)

Mostrar que si una función\(T :\mathbb{R}^n → \mathbb{R}^m\) es lineal, entonces siempre es el caso que\(T(\vec{0})=\vec{0}\).

Ejercicio\(\PageIndex{18}\)

Dejar\(T\) ser una transformación lineal inducida por la matriz\(A=\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]\) y\(S\) una transformación lineal inducida por\(B=\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\). Encontrar matriz de\(S\circ T\) y buscar\((S\circ T)(\vec{x})\) para\(\vec{x}=\left[\begin{array}{r}2\\-1\end{array}\right]\).

Contestar

La matriz de\(S\circ T\) está dada por\(BA\). \[\left[\begin{array}{cc}0&-2\\4&2\end{array}\right]\left[\begin{array}{cc}3&1\\-1&2\end{array}\right]=\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\nonumber\]Ahora,\((S\circ T)(\vec{x})=(BA)\vec{x}\). \[\left[\begin{array}{cc}2&-4\\10&8\end{array}\right]\left[\begin{array}{c}2\\-1\end{array}\right]=\left[\begin{array}{c}8\\12\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{19}\)

Dejar\(T\) ser una transformación lineal y supongamos\(T\left(\left[\begin{array}{r}1\\-4\end{array}\right]\right)=\left[\begin{array}{r}2\\-3\end{array}\right]\). Supongamos que\(S\) es una transformación lineal inducida por la matriz\(B=\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\). Encuentra\((S\circ T)(\vec{x})\) para\(\vec{x}=\left[\begin{array}{r}1\\-4\end{array}\right]\).

Contestar

Para encontrar\((S\circ T)(\vec{x})\) calculamos\(S(T(\vec{x}))\). \[\left[\begin{array}{cc}1&2\\-1&3\end{array}\right]\left[\begin{array}{c}2\\-3\end{array}\right]=\left[\begin{array}{c}-4\\-11\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{20}\)

Dejar\(T\) ser una transformación lineal inducida por la matriz\(A=\left[\begin{array}{cc}2&3\\1&1\end{array}\right]\) y\(S\) una transformación lienar inducida por\(B=\left[\begin{array}{cc}-1&3\\1&-2\end{array}\right]\). Encontrar matriz de\(S\circ T\) y buscar\((S\circ T)(\vec{x})\) para\(\vec{x}=\left[\begin{array}{c}5\\6\end{array}\right]\).

Ejercicio\(\PageIndex{21}\)

Dejar\(T\) ser una transformación lineal inducida por la matriz\(A=\left[\begin{array}{cc}2&1\\5&2\end{array}\right]\). Encuentra la matriz de\(T^{-1}\).

Contestar

La matriz de\(T^{-1}\) es\(A^{-1}\). \[\left[\begin{array}{cc}2&1\\5&2\end{array}\right]^{-1}=\left[\begin{array}{cc}-2&1\\5&-2\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{22}\)

Dejar\(T\) ser una transformación lineal inducida por la matriz\(A=\left[\begin{array}{cc}4&-3\\2&-2\end{array}\right]\). Encuentra la matriz de\(T^{-1}\).

Ejercicio\(\PageIndex{23}\)

Dejar\(T\) ser una transformación lineal y supongamos\(T\left(\left[\begin{array}{c}1\\2\end{array}\right]\right)=\left[\begin{array}{c}9\\8\end{array}\right],\:T\left(\left[\begin{array}{r}0\\-1\end{array}\right]\right)=\left[\begin{array}{c}-4\\-3\end{array}\right]\). Encuentra la matriz de\(T^{-1}\).

Ejercicio\(\PageIndex{24}\)

Encuentra la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) en un ángulo de\(π/3\).

Contestar

\(\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\)

Ejercicio\(\PageIndex{25}\)

Encuentra la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) en un ángulo de\(π/4\).

Contestar

\(\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\)

Ejercicio\(\PageIndex{26}\)

Encuentra la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) en un ángulo de\(-π/3\).

Contestar

\(\left[\begin{array}{cc}\cos\left(-\frac{\pi}{3}\right)&-\sin\left(-\frac{\pi}{3}\right) \\ \sin\left(-\frac{\pi}{3}\right)&\cos\left(-\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&\frac{1}{2}\sqrt{3} \\ -\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\)

Ejercicio\(\PageIndex{27}\)

Encuentra la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) en un ángulo de\(2π/3\).

Contestar

\(\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\)

Ejercicio\(\PageIndex{28}\)

Encuentra la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) en un ángulo de\(π/12\). Pista: Tenga en cuenta que\(\pi /12=\pi /3-\pi /4\).

Contestar

\[\begin{aligned}&\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right] \\ =&\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}-\frac{1}{4}\sqrt{2}\sqrt{3} \\ \frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}\end{array}\right]\end{aligned}\]

Ejercicio\(\PageIndex{29}\)

Encuentre la matriz para la transformación lineal que gira cada vector en\(\mathbb{R}^2\) un ángulo de\(2π/3\) y luego se refleja a través del\(x\) eje.

Contestar

\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&\frac{1}{2}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{30}\)

Encuentre la matriz para la transformación lineal que gira cada vector en\(\mathbb{R}^2\) un ángulo de\(π/3\) y luego se refleja a través del\(x\) eje.

Contestar

\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{3}\right)&-\sin\left(\frac{\pi}{3}\right) \\ \sin\left(\frac{\pi}{3}\right)&\cos\left(\frac{\pi}{3}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}&-\frac{1}{2}\sqrt{3}\\-\frac{1}{2}\sqrt{3}&-\frac{1}{2}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{31}\)

Encuentre la matriz para la transformación lineal que gira cada vector en\(\mathbb{R}^2\) un ángulo de\(π/4\) y luego se refleja a través del\(x\) eje.

Contestar

\[\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\\-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{32}\)

Encuentre la matriz para la transformación lineal que gira cada vector en\(\mathbb{R}^2\) un ángulo de\(π/6\) y luego se refleja a través del\(x\) eje seguido de una reflexión a través del\(y\) eje.

Contestar

\[\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&\frac{1}{2}\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{33}\)

Encuentre la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) a través del\(x\) eje y luego gira cada vector a través de un ángulo de\(\pi /4\).

Contestar

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{34}\)

Encuentre la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) a través del\(y\) eje y luego gira cada vector a través de un ángulo de\(\pi /4\).

Contestar

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{4}\right)&-\sin\left(\frac{\pi}{4}\right) \\ \sin\left(\frac{\pi}{4}\right)&\cos\left(\frac{\pi}{4}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{2}&-\frac{1}{2}\sqrt{2} \\ -\frac{1}{2}\sqrt{2}&\frac{1}{2}\sqrt{2}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{35}\)

Encuentre la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) a través del\(x\) eje y luego gira cada vector a través de un ángulo de\(\pi /6\).

Contestar

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}\sqrt{3}&\frac{1}{2} \\ \frac{1}{2}&-\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{36}\)

Encuentre la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) a través del\(y\) eje y luego gira cada vector a través de un ángulo de\(\pi /6\).

Contestar

\[\left[\begin{array}{cc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right) \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)\end{array}\right]\left[\begin{array}{cc}-1&0\\0&1\end{array}\right]=\left[\begin{array}{cc}-\frac{1}{2}\sqrt{3}&-\frac{1}{2} \\ -\frac{1}{2}&\frac{1}{2}\sqrt{3}\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{37}\)

Encuentra la matriz para la transformación lineal que gira cada vector\(\mathbb{R}^2\) en un ángulo de\(5\pi /12\). Pista: Tenga en cuenta que\(5\pi /12=2\pi /3-\pi /4\).

Contestar

\[\left[\begin{array}{cc}\cos\left(\frac{2\pi}{3}\right)&-\sin\left(\frac{2\pi}{3}\right) \\ \sin\left(\frac{2\pi}{3}\right)&\cos\left(\frac{2\pi}{3}\right)\end{array}\right]\left[\begin{array}{cc}\cos\left(-\frac{\pi}{4}\right)&-\sin\left(-\frac{\pi}{4}\right) \\ \sin\left(-\frac{\pi}{4}\right)&\cos\left(-\frac{\pi}{4}\right)\end{array}\right]=\nonumber\]\[\left[\begin{array}{cc}\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}&-\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2} \\ \frac{1}{4}\sqrt{2}\sqrt{3}+\frac{1}{4}\sqrt{2}&\frac{1}{4}\sqrt{2}\sqrt{3}-\frac{1}{4}\sqrt{2}\end{array}\right]\nonumber\]Tenga en cuenta que no importa el orden en este caso.

Ejercicio\(\PageIndex{38}\)

Encuentre la matriz de la transformación lineal que gira cada vector en sentido\(\mathbb{R}^3\) contrario a las agujas del reloj alrededor del\(z\) eje cuando se ve desde el\(z\) eje positivo a través de un ángulo de\(30^◦\) y luego se refleja a través del\(xy\) plano.

Contestar

\[\left[\begin{array}{ccc}1&0&0\\0&1&0\\0&0&-1\end{array}\right]\left[\begin{array}{ccc}\cos\left(\frac{\pi}{6}\right)&-\sin\left(\frac{\pi}{6}\right)&0 \\ \sin\left(\frac{\pi}{6}\right)&\cos\left(\frac{\pi}{6}\right)&0 \\ 0&0&1\end{array}\right]=\left[\begin{array}{ccc}\frac{1}{2}\sqrt{3}&-\frac{1}{2}&0\\ \frac{1}{2}&\frac{1}{2}\sqrt{3}&0\\0&0&-1\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{39}\)

Dejar\(\vec{u}=\left[\begin{array}{c}a\\b\end{array}\right]\) ser un vector de unidad en\(\mathbb{R}^2\). Encuentre la matriz que refleja todos los vectores a través de este vector, como se muestra en la siguiente imagen.

Figura\(\PageIndex{1}\)

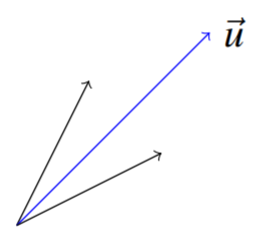
Pista: Observe que\(\left[\begin{array}{c}a\\b\end{array}\right]=\left[\begin{array}{c}\cos\theta \\ \sin\theta\end{array}\right]\) para algunos\(\theta\). Primero rote a través\(-\theta\). A continuación reflexionar a través del\(x\) eje. Finalmente rote a través\(\theta\).

Contestar

\[\begin{aligned} &\left[\begin{array}{cc}\cos (\theta )&-\sin(\theta) \\ \sin(\theta)&\cos(\theta)\end{array}\right]\left[\begin{array}{cc}1&0\\0&-1\end{array}\right]\left[\begin{array}{cc}\cos(-\theta)&-\sin(\theta) \\ \sin(-\theta)&\cos(-\theta)\end{array}\right] \\ =&\left[\begin{array}{cc}\cos^2\theta-\sin^2\theta &2\cos\theta\sin\theta \\ 2\cos\theta\sin\theta&\sin^2\theta-\cos^2\theta\end{array}\right]\end{aligned}\]Ahora para escribir en términos de\((a,b)\), tenga en cuenta que\(a/\sqrt{a^2+b^2}=\cos\theta\),\(b/\sqrt{a^2+b^2}=\sin\theta\). Ahora enchufa esto a lo anterior. El resultado es\[\left[\begin{array}{cc}\frac{a^2-b^2}{a^2+b^2}&2\frac{ab}{a^2+b^2} \\ 2\frac{ab}{a^2+b^2}&\frac{b^2-a^2}{a^2+b^2}\end{array}\right]=\frac{1}{a^2+b^2}\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber\] Dado que se trata de un vector unitario,\(a^2+b^2=1\) y así se obtiene\[\left[\begin{array}{cc}a^2-b^2&2ab \\ 2ab&b^2-a^2\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{40}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}2&1\\0&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] ¿Es\(T\) uno a uno? ¿Está\(T\) onto?

Ejercicio\(\PageIndex{41}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}-1&2\\2&1\\1&4\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] ¿Es\(T\) uno a uno? ¿Está\(T\) onto?

Ejercicio\(\PageIndex{42}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}2&0&1\\1&2&-1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] ¿Es\(T\) uno a uno? ¿Está\(T\) onto?

Ejercicio\(\PageIndex{43}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&3&-5\\2&0&2\\2&4&-6\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] ¿Es\(T\) uno a uno? ¿Está\(T\) onto?

Ejercicio\(\PageIndex{44}\)

Dé un ejemplo de una\(3\times 2\) matriz con la propiedad de que la transformación lineal determinada por esta matriz es uno a uno pero no sobre.

Contestar

\[\left[\begin{array}{cc}1&0\\0&1\\0&0\end{array}\right]\nonumber\]

Ejercicio\(\PageIndex{45}\)

Supongamos que\(A\) es una\(m\times n\) matriz en la que\(m ≤ n\). Supongamos también que el rango de\(A\) iguales\(m\). Mostrar que la transformación\(T\) determinada por\(A\) mapas\(\mathbb{R}^n\) en\(\mathbb{R}^m\). Pista: Los vectores\(\vec{e}_1,\cdots ,\vec{e}_m\) aparecen como columnas en la forma de escalón de fila-escalón reducido para\(A\).

Contestar

Esto dice que las columnas de\(A\) tienen un subconjunto de\(m\) vectores que son linealmente independientes. Por lo tanto, este conjunto de vectores es una base para\(\mathbb{R}^m\). De ello se deduce que el lapso de las columnas es todo de\(\mathbb{R}^m\). Así\(A\) está sobre.

Ejercicio\(\PageIndex{46}\)

Supongamos que\(A\) es una\(m\times n\) matriz en la que\(m ≥ n\). Supongamos también que el rango de\(A\) iguales\(n\). Demostrar que\(A\) es uno a uno. Pista: Si no, existe un vector,\(\vec{x}\) tal que\(A\vec{x} = 0\), y esto implica al menos una columna de\(A\) es una combinación lineal de las otras. Mostrar esto requeriría que el rango sea menor que\(n\).

Contestar

Las columnas son independientes. Por lo tanto,\(A\) es uno a uno.

Ejercicio\(\PageIndex{47}\)

Explique por qué una\(n\times n\) matriz\(A\) es a la vez uno a uno y sobre si y solo si su rango es\(n\).

Contestar

El rango es\(n\) es lo mismo que decir que las columnas son independientes lo cual es lo mismo que decir\(A\) es uno a uno que es lo mismo que decir que las columnas son una base. Por lo tanto, el lapso de las columnas de\(A\) es todo\(\mathbb{R}^n\) y así\(A\) está encendido. Si\(A\) está on, entonces las columnas deben ser linealmente independientes ya que de lo contrario el lapso de estas columnas tendría una dimensión menor que\(n\) y así la dimensión de\(\mathbb{R}^n\) sería menor que\(n\).

Ejercicio\(\PageIndex{48}\)

Dejar\(V\) y\(W\) ser subespacios de\(\mathbb{R}^n\) y\(\mathbb{R}^m\) respectivamente y dejar\(T : V → W\) ser una transformación lineal. Supongamos que\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) es linealmente independiente. Demostrar que debe ser el caso que también\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) sea linealmente independiente.

Contestar

Si\(\sum_i^r a_i\vec{v}_r=0\), entonces usando las propiedades de linealidad de\(T\) obtenemos\[0=T(0)=T\left(\sum\limits_i^ra_i\vec{v}_r\right)=\sum\limits_i^ra_iT(\vec{v}_r).\nonumber\] Ya que asumimos que\(\{T\vec{v}_a,\cdots ,T\vec{v}_r\}\) es linealmente independiente, debemos tener todo\(a_i = 0\), y por lo tanto concluimos que también\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) es linealmente independiente.

Ejercicio\(\PageIndex{49}\)

\[V=span\left\{\left[\begin{array}{c}1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\0\\1\end{array}\right]\right\}\nonumber\]Let Let\(T\vec{x}=A\vec{x}\) donde\(A\) esta la matriz\[\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber\] Dar una base para\(im(T)\).

Ejercicio\(\PageIndex{50}\)

\[V=span\left\{\left[\begin{array}{c}1\\0\\0\\1\end{array}\right],\:\left[\begin{array}{c}1\\1\\1\\1\end{array}\right],\:\left[\begin{array}{c}1\\4\\4\\1\end{array}\right]\right\}\nonumber\]Let Let\(T\vec{x}=A\vec{x}\) donde\(A\) esta la matriz\[\left[\begin{array}{cccc}1&1&1&1\\0&1&1&0\\0&1&2&1\\1&1&1&2\end{array}\right]\nonumber\] Encontrar una base para\(im(T)\). En este caso, los vectores originales no forman un conjunto independiente.

Contestar

Dado que el tercer vector es una combinación lineal de los dos primeros, entonces la imagen del tercer vector también será una combinación lineal de la imagen de los dos primeros. Sin embargo, la imagen de los dos primeros vectores son linealmente independientes (¡check!) , y de ahí formar una base de la imagen.

Por lo tanto, una base para\(im(T)\) es:\[V=span\left\{\left[\begin{array}{c}2\\0\\1\\3\end{array}\right],\:\left[\begin{array}{c}4\\2\\4\\5\end{array}\right]\right\}\nonumber\]

Ejercicio\(\PageIndex{51}\)

Si\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) es linealmente independiente y\(T\) es una transformación lineal uno a uno, mostrar que también\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) es linealmente independiente. Dar un ejemplo que demuestre que si sólo\(T\) es lineal, puede suceder que, aunque\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) es linealmente independiente, no lo\(\{T\vec{v}_1,\cdots ,T\vec{v}_r\}\) es. De hecho, muestran que puede suceder que cada uno de los\(T\vec{v}_j\) iguales\(0\).

Ejercicio\(\PageIndex{52}\)

Dejar\(V\) y\(W\) ser subespacios de\(\mathbb{R}^n\) y\(\mathbb{R}^m\) respectivamente y dejar\(T : V → W\) ser una transformación lineal. Demuestre que si\(T\) está\(W\) encendido y si\(\{\vec{v}_1,\cdots ,\vec{v}_r\}\) es una base para\(V\), entonces\(span\{T\vec{v}_1,\cdots ,T\vec{v}_r\} = W\).

Ejercicio\(\PageIndex{53}\)

Definir\(T\): de\(\mathbb{R}^4\to\mathbb{R}^3\) la siguiente manera. \[T\vec{x}=\left[\begin{array}{cccc}3&2&1&8\\2&2&-2&6\\1&1&-1&3\end{array}\right]\vec{x}\nonumber\]Encuentra una base para\(im(T)\). También encuentra una base para\(\text{ker}(T)\).

Ejercicio\(\PageIndex{54}\)

Definir\(T\): de\(\mathbb{R}^3\to\mathbb{R}^3\) la siguiente manera. \[T\vec{x}=\left[\begin{array}{ccc}1&2&0\\1&1&1\\0&1&1\end{array}\right]\vec{x}\nonumber\]donde a la derecha, es solo la multiplicación matricial del vector\(\vec{x}\) que se entiende. Explicar por qué\(T\) es un isomorfismo de\(\mathbb{R}^3\) a\(\mathbb{R}^3\).

Ejercicio\(\PageIndex{55}\)

Supongamos\(T\):\(\mathbb{R}^3\to\mathbb{R}^3\) es una transformación lineal dada por\[T\vec{x}=A\vec{x}\nonumber\] donde\(A\) es una\(3\times 3\) matriz. Demostrar que\(T\) es un isomorfismo si y sólo si\(A\) es invertible.

Ejercicio\(\PageIndex{56}\)

Supongamos\(T\):\(\mathbb{R}^n\to\mathbb{R}^m\) es una transformación lineal dada por\[T\vec{x}=A\vec{x}\nonumber\] donde\(A\) es una\(m\times n\) matriz. Demostrar que nunca\(T\) es un ismorfismo si\(m\neq n\). En particular, mostrar que si\(m>n\),\(T\) no puede estar encendido y si\(m<n\), entonces\(T\) no puede ser uno a uno.

Ejercicio\(\PageIndex{57}\)

Definir\(T\): de\(\mathbb{R}^2\to\mathbb{R}^3\) la siguiente manera. \[T\vec{x}=\left[\begin{array}{cc}1&0\\1&1\\0&1\end{array}\right]\vec{x}\nonumber\]donde a la derecha, es solo la multiplicación matricial del vector\(\vec{x}\) que se entiende. Demostrar que\(T\) es uno a uno. Siguiente vamos\(W = im(T)\). Demostrar que\(T\) es un isomorfismo de\(\mathbb{R}^2\) y\(im (T)\).

Ejercicio\(\PageIndex{58}\)

En el problema anterior, encuentra una\(2\times 3\) matriz\(A\) tal que la restricción de\(A\) a\(im(T)\) da el mismo resultado que\(T^{−1}\) on\(im(T)\). Pista: Podrías dejar\(A\) ser tal que\[A\left[\begin{array}{c}1\\1\\0\end{array}\right]=\left[\begin{array}{c}1\\0\end{array}\right],\:A\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\end{array}\right]\nonumber\] ahora encuentre otro vector\(\vec{v}\in\mathbb{R}^3\) tal que\[\left\{\left[\begin{array}{c}1\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right],\:\vec{v}\right\}\nonumber\] sea una base. Podrías escoger\[\vec{v}=\left[\begin{array}{c}0\\0\\1\end{array}\right]\nonumber\] por ejemplo. Explica por qué este funciona o uno de tu elección funciona. Entonces podrías definir\(A\vec{v}\) para igualar algún vector en\(\mathbb{R}^2\). Explique por qué habrá más de una matriz de este tipo\(A\) que entregará el isomorfismo inverso\(T^{−1}\) sobre\(im(T)\).

Ejercicio\(\PageIndex{59}\)

Ahora vamos\(V\) equan\(span\left\{\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\right\}\) y vamos\(T\):\(V\to W\) ser una transformación lineal donde\[W=span\left\{\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\right\}\nonumber\] y\[T\left[\begin{array}{c}1\\0\\1\end{array}\right]=\left[\begin{array}{c}1\\0\\1\\0\end{array}\right],\:T\left[\begin{array}{c}0\\1\\1\end{array}\right]=\left[\begin{array}{c}0\\1\\1\\1\end{array}\right]\nonumber\] Explique por qué\(T\) es un isomorfismo. Determinar una matriz\(A\) que, cuando se multiplica a la izquierda da el mismo resultado que\(T\) on\(V\) y una matriz\(B\) que entrega\(T^{−1}\) encendido\(W\). Pista: Necesitas tener\[A\left[\begin{array}{cc}1&0\\0&1\\1&1\end{array}\right]=\left[\begin{array}{cc}1&0\\0&1\\1&1\\0&1\end{array}\right]\nonumber\] Ahora agrandar\(\left[\begin{array}{c}1\\0\\1\end{array}\right],\:\left[\begin{array}{c}0\\1\\1\end{array}\right]\) para obtener una base para\(\mathbb{R}^3\). Podrías agregar\(\left[\begin{array}{c}0\\0\\1\end{array}\right]\) por ejemplo, y luego elegir otro vector\(\mathbb{R}^4\) y dejar que\(A\left[\begin{array}{c}0\\0\\1\end{array}\right]\) sea igual a este otro vector. Entonces tendrías\[A\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&1\end{array}\right]=\left[\begin{array}{ccc}1&0&0\\0&1&0\\1&1&0\\0&1&1\end{array}\right]\nonumber\] Esto implicaría escoger para el nuevo vector en\(\mathbb{R}^4\) el vector\(\left[\begin{array}{cccc}0&0&0&1\end{array}\right]^T\). Entonces podrías encontrar\(A\). Se puede hacer algo similar para encontrar una matriz para\(T^{−1}\) denotada como\(B\).

Ejercicio\(\PageIndex{60}\)

Let\(V=\mathbb{R}^3\) y let\[W=span(S),\text{ where }S=\left\{\left[\begin{array}{r}1\\-1\\1\end{array}\right],\:\left[\begin{array}{r}-2\\2\\-2\end{array}\right],\:\left[\begin{array}{r}-1\\1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\\3\end{array}\right]\right\}\nonumber\] Encuentra una base de\(W\) que consiste en vectores en\(S\).

Contestar

En este caso\(\text{dim}(W) = 1\) y se\(S\) puede obtener una base para\(W\) constar de vectores en tomando cualquier vector (distinto de cero) de\(S\).

Ejercicio\(\PageIndex{61}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&1\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Encontrar una base para\(\text{ker}(T)\) y\(im(T)\).

Contestar

Una base para\(\text{ker}(T)\) es\(\left\{\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\) y una base para\(im(T)\) es\(\left\{\left[\begin{array}{c}1\\1\end{array}\right]\right\}\). Hay muchas otras posibilidades para las bases específicas, pero en este caso\(\text{dim}(\text{ker}(T))=1\) y\(\text{dim}(im(T))=1\).

Ejercicio\(\PageIndex{62}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\end{array}\right]=\left[\begin{array}{cc}1&0\\1&1\end{array}\right]\left[\begin{array}{c}x\\y\end{array}\right]\nonumber\] Encontrar una base para\(\text{ker}(T)\) y\(im(T)\).

Contestar

En este caso\(\text{ker}(T)=\{0\}\) y\(im(T)=\mathbb{R}^2\) (escoger cualquier base de\(\mathbb{R}^2\)).

Ejercicio\(\PageIndex{63}\)

Dejar\(V=\mathbb{R}^3\) y dejar\[W=span\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right]\right\}\nonumber\] Extender esta base de\(W\) a una base de\(V\).

Contestar

Hay muchas posibles extensiones de este tipo, una es (¿cómo sabemos?) :\[\left\{\left[\begin{array}{c}1\\1\\1\end{array}\right],\:\left[\begin{array}{r}-1\\2\\-1\end{array}\right],\:\left[\begin{array}{c}0\\0\\1\end{array}\right]\right\}\nonumber\]

Ejercicio\(\PageIndex{64}\)

Dejar\(T\) ser una transformación lineal dada por\[T\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{ccc}1&1&1\\1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]\nonumber\] ¿Qué es\(\text{dim}(\text{ker}(T))\)?

Contestar

Eso lo podemos ver fácilmente\(\text{dim}(im(T))=1\), y así\(\text{dim}(\text{ker}(T))=3-\text{dim}(im(T))=3-1=2\).

Ejercicio\(\PageIndex{65}\)

Dejar\(B=\left\{\left[\begin{array}{r}2\\-1\end{array}\right],\:\left[\begin{array}{r}3\\2\end{array}\right]\right\}\) ser una base de\(\mathbb{R}^2\) y dejar\(\vec{x}=\left[\begin{array}{r}5\\-7\end{array}\right]\) ser un vector en\(\mathbb{R}^2\). Encuentra\(C_B(\vec{x})\).

Ejercicio\(\PageIndex{66}\)

Dejar\(B=\left\{\left[\begin{array}{r}1\\-1\\2\end{array}\right],\:\left[\begin{array}{r}2\\1\\2\end{array}\right],\:\left[\begin{array}{r}-1\\0\\2\end{array}\right]\right\}\) ser una base de\(\mathbb{R}^3\) y dejar\(\vec{x}=\left[\begin{array}{r}5\\-1\\4\end{array}\right]\) ser un vector en\(\mathbb{R}^2\). Encuentra\(C_B(\vec{x})\).

Contestar

\(C_B(\vec{x})=\left[\begin{array}{r}2\\1\\-1\end{array}\right]\)

Ejercicio\(\PageIndex{67}\)

Let\(T\):\(\mathbb{R}^2→\mathbb{R}^2\) ser una transformación lineal definida por\(T\left(\left[\begin{array}{c}a\\b\end{array}\right)\right]=\left[\begin{array}{c}a+b\\a-b\end{array}\right]\).

Considera las dos bases\[B_1=\{\vec{v}_1,\vec{v}_2\}=\left\{\left[\begin{array}{c}1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\end{array}\right]\right\}\nonumber\] y\[B_2=\left\{\left[\begin{array}{c}1\\1\end{array}\right],\:\left[\begin{array}{r}1\\-1\end{array}\right]\right\}\nonumber\]

Encuentra la matriz\(M_{B_2,B_1}\) de\(T\) con respecto a las bases\(B_1\) y\(B_2\).

Contestar

\(M_{B_2B_1}=\left[\begin{array}{rr}1&0\\-1&1\end{array}\right]\)

Ejercicio \(\PageIndex{68}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-3\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}_3\in\mathbb{R}\). Una base para el espacio de solución es\(\left[\begin{array}{r}-3\\-1\\1\end{array}\right]\nonumber\)

Ejercicio\(\PageIndex{69}\)

Utilizando Exercise\(\PageIndex{68}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{rrr}1&-1&2\\1&-2&1\\3&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber\]

Contestar

Tenga en cuenta que esto tiene la misma matriz que el problema anterior. La solución es:\(\left[\begin{array}{r}-3\hat{t}_3 \\ -\hat{t}_3 \\ \hat{t}_3\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}_3\in\mathbb{R}\)

Ejercicio \(\PageIndex{70}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]\), Una base es\(\left[\begin{array}{c}3\\2\\1\end{array}\right]\)

Ejercicio\(\PageIndex{71}\)

Utilizando Exercise\(\PageIndex{70}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{rrr}0&-1&2\\1&-2&1\\1&-4&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{c}3\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right] +\left[\begin{array}{c}-3\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Ejercicio \(\PageIndex{72}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores. \[\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]\). Una base es\(\left[\begin{array}{r}-4\\-2\\1\end{array}\right]\)

Ejercicio\(\PageIndex{73}\)

Utilizando Exercise\(\PageIndex{72}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{ccc}1&-1&2\\1&-2&0\\3&-4&4\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\2\\4\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-4\hat{t} \\ -2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}0\\-1\\0\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Ejercicio \(\PageIndex{74}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Ejercicio\(\PageIndex{75}\)

Utilizando Exercise\(\PageIndex{74}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{ccc}0&-1&2\\1&0&1\\1&-2&5\end{array}\right]\left[\begin{array}{c}x\\y\\z\end{array}\right]=\left[\begin{array}{c}1\\-1\\1\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-\hat{t} \\ 2\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}-1\\-1\\0\end{array}\right]\)

Ejercicio \(\PageIndex{76}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right],\:\hat{t}\in\mathbb{R}\)

Ejercicio\(\PageIndex{77}\)

Utilizando Exercise\(\PageIndex{76}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{cccc}1&0&1&1\\1&-1&1&0\\3&-1&3&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}0\\ -\hat{t} \\ -\hat{t} \\ \hat{t}\end{array}\right]+\left[\begin{array}{r}2\\-1\\-1\\0\end{array}\right]\)

Ejercicio \(\PageIndex{78}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{cccc}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&0&0&0\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{c}-s-t \\ s\\s\\t\end{array}\right],\:s,t\in\mathbb{R}\). Una base es\[\left\{\left[\begin{array}{r}-1\\1\\1\\0\end{array}\right],\:\left[\begin{array}{r}-1\\0\\0\\1\end{array}\right]\right\}\nonumber\]

Ejercicio\(\PageIndex{79}\)

Utilizando Exercise\(\PageIndex{78}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\[\left[\begin{array}{r}-\hat{t}\\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{c}-8\\5\\0\\5\end{array}\right]\nonumber\]

Ejercicio \(\PageIndex{80}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\[\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber\] para\(s,t\in\mathbb{R}\). Una base es\[\left\{\left[\begin{array}{r}-1\\1\\2\\0\end{array}\right],\:\left[\begin{array}{r}-1\\1\\0\\1\end{array}\right]\right\}\nonumber\]

Ejercicio\(\PageIndex{81}\)

Utilizando Exercise\(\PageIndex{80}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{rrrr}1&1&0&1\\1&-1&1&0\\3&1&1&2\\3&3&0&3\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}1\\2\\4\\3\end{array}\right]\nonumber\]

Contestar

La solución es:\[\left[\begin{array}{r}\frac{3}{2} \\ -\frac{1}{2}\\0\\0\end{array}\right]+\left[\begin{array}{c}-\frac{1}{2}s-\frac{1}{2}t \\ \frac{1}{2}s-\frac{1}{2}t \\ s\\t\end{array}\right]\nonumber\]

Ejercicio \(\PageIndex{82}\)

Escriba el conjunto de soluciones del siguiente sistema como una combinación lineal de vectores\[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{c}0\\0\\0\\0\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]\), una base es\(\left[\begin{array}{c}1\\1\\1\\0\end{array}\right]\).

Ejercicio\(\PageIndex{83}\)

Utilizando Exercise\(\PageIndex{82}\) encuentra la solución general al siguiente sistema lineal. \[\left[\begin{array}{rrrr}1&1&0&1\\2&1&1&2\\1&0&1&1\\0&-1&1&1\end{array}\right]\left[\begin{array}{c}x\\y\\z\\w\end{array}\right]=\left[\begin{array}{r}2\\-1\\-3\\1\end{array}\right]\nonumber\]

Contestar

La solución es:\(\left[\begin{array}{r}-\hat{t} \\ \hat{t} \\ \hat{t}\\0\end{array}\right]+\left[\begin{array}{r}-9\\5\\0\\6\end{array}\right],t\in\mathbb{R}\).

Ejercicio\(\PageIndex{84}\)

Supongamos que\(A\vec{x}=\vec{b}\) tiene una solución. Explique por qué la solución es única precisamente cuando solo\(A\vec{x}=\vec{0}\) tiene la solución trivial.

Contestar

De no ser así, entonces habría infinitamente muchas soluciones a\(A\vec{x}=\vec{0}\) y cada una de estas sumadas a una solución para\(A\vec{x}=\vec{b}\) ser una solución para\(A\vec{x}=\vec{b}\).