3.4: Coloración de dominio

Retratos de fase compleja

Una forma de visualizar funciones complejas\(f:\mathbb{C}\rightarrow \mathbb{C}\) es usando retratos de fase. A un número complejo se le puede asignar un color de acuerdo a su argumento/fase. Los números positivos son de color rojo; los números negativos se colorean en cian y los números con una parte imaginaria diferente de cero se colorean como en la Figura 1, que muestra un retrato de fase para la función\(f(z)=z\).

Figura 1: Retrato de fase de\(f(z)=z\).

En su libro Visual Complex Functions, Elias Wegert emplea retratos de fase con curvas de nivel de fase y módulo (retratos de fase mejorados) para el estudio de la teoría de funciones complejas. Consulte por ejemplo las Figuras 2 y 3 para la función\(f(z)=z\).

Figura 2: Líneas de contorno de fase.

Figura 3: Líneas de contorno de módulo.

Decimos que una funcion compleja\(f\) tiene una raíz (o un cero) en\(z_{0}\), si\(f\left ( z_{0} \right )\). Decimos que\(z_{0}\) es un polo cuando\(f\left ( z_{0} \right )\) está indefinido. Con el uso de retratos de fase mejorados, las raíces y los polos de una función compleja se\(f(z)\) pueden ver fácilmente en los puntos donde se encuentran todos los colores. Las figuras 4 y 5 muestran el retrato de fase mejorado de las funciones.

\(f(z)=z\)y\(g(z)=1/z\),

respectivamente. Observe el contraste entre las curvas de nivel de módulo en cada caso.

Figura 4: Raíz en\(z=0\).

Figura 5: Polo en\(z=0\).

Consideremos ahora la función

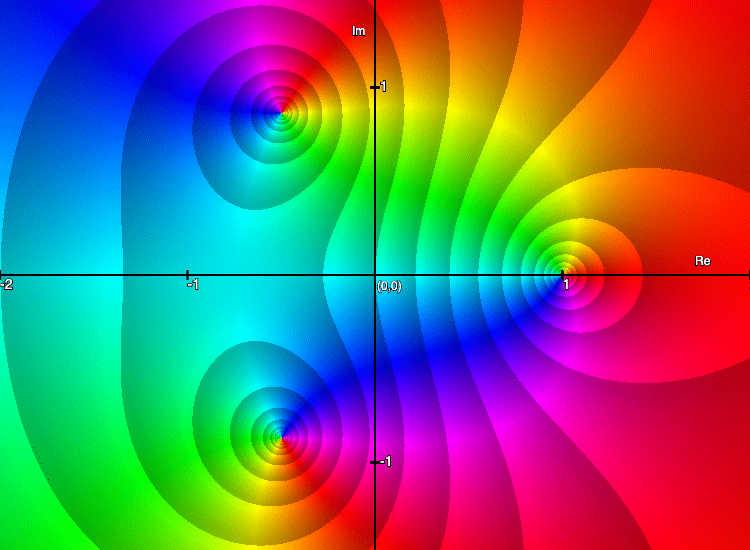
\(f\left ( z \right )=\frac{z-1}{z^{2}+z+1}\)(1)

que tiene una raíz en\(z_{0}=1\) y dos polos en

\(z_{1}=\frac{-1+\sqrt{3}i}{2}\)y\(z_{2}=\frac{-1-\sqrt{3}i}{2}\).

La Figura 6 muestra el retrato mejorado de (1) con curvas de nivel del módulo. Observe el comportamiento de las curvas de nivel del módulo alrededor de la raíz (lado derecho) y los polos (lado izquierdo). ¿Ves la diferencia?

Figura 6: Gráfica de curvas\(f(z)=(z−1)/(z2+z+1)\) con nivel del módulo.

---

Explora funciones complejas

Utilice el applet a continuación para explorar retratos de fase mejorados de funciones complejas.

GRAFO INTERACTIVO

---

¡Advertencia!

Si no imponemos restricciones adicionales, como continuidad o diferenciabilidad, los conjuntos isocromáticos de funciones complejas pueden ser arbitrarios, pero esto no es así para las funciones analíticas, que son los objetos de primer interés en este texto.

De hecho, las funciones analíticas están (casi) singularmente determinadas por sus retratos de fase (puros), pero esto no es así para las funciones generales. Por ejemplo, las funciones\(f\) (analíticas) y\(g\) (no analíticas) definidas por

\(f\left ( z \right )=\frac{z-1}{z^{2}+z+1}\),\(g\left ( z \right )=\left ( z-1 \right )\left ( \bar{z} ^{2}+\bar{z}+1\right )\) (2)

tienen la misma fase (excepto en sus ceros y polos) aunque son completamente diferentes.

Dado que los retratos de fase pura no siempre muestran suficiente información para explorar funciones complejas generales, recomiendo el uso de sus versiones mejoradas con curvas de nivel de módulo y fase en tales casos. La Figura 7 muestra dos retratos de las funciones\(f\) (izquierda) y\(g\) (derecha) definidas en (2).

Figura 7: Retratos de fase mejorados de\(f\) (izquierda) y\(g\) (derecha). Deslizador de arrastre.

Una distinción notable entre los dos retratos es la forma de los azulejos. En la imagen de la izquierda la mayoría de ellos son casi cuadrados y tienen esquinas en ángulo recto. Por el contrario, muchas fichas en el retrato de\(g\) son proladas y sus ángulos difieren significativamente de\(\pi /2\) - en algunos puntos las líneas de contorno del módulo y la fase son incluso mutuamente tangentes.