5.1: Serie
- Page ID
- 114087
Serie
Convergencia de Secuencias
Una secuencia infinita\(\left\{z_1,z_2,z_3 \ldots\right\}\) de números complejos tiene un límite\(z\) si, para cada número positivo\(ε\), existe un entero positivo\(n_0\) tal que
\ (\ begin {eqnarray}\ label {seq}
\ izquierda|z_n-z\ derecha|<\ varepsilon\ quad\ text {whenever}\ quad n > n_0.
\ end {eqnarray}\)
Geométricamente, esto significa que para valores suficientemente grandes de\(n\), los puntos se\(z_n\) encuentran en cualquier\(ε\) vecindario dado de\(z\) (Figura 1). Dado que podemos elegir\(ε\) lo pequeño que queramos, se deduce que los puntos\(z_n\) se acercan arbitrariamente a\(z\) medida que aumentan sus subíndices. Tenga en cuenta que el valor de\(n_0\) que se necesite dependerá, en general, del valor de\(ε\).
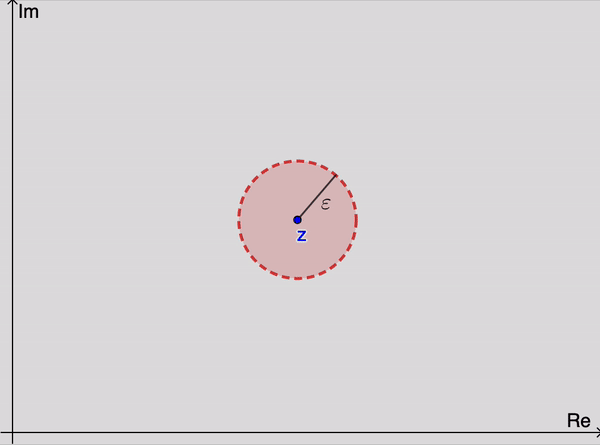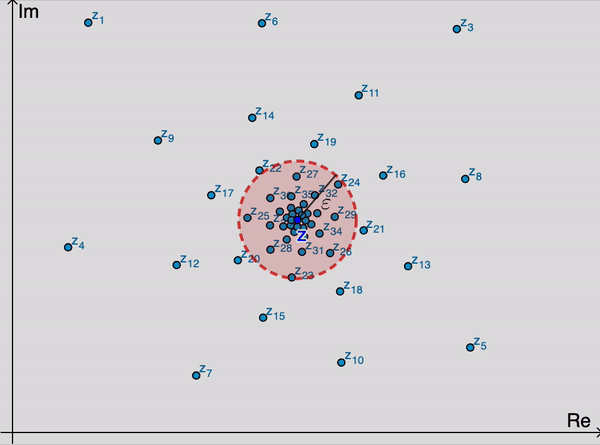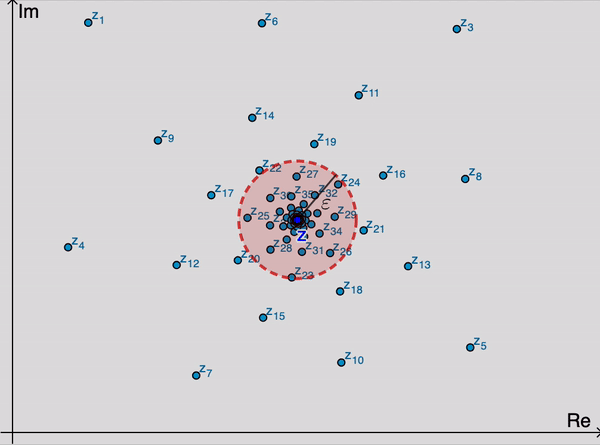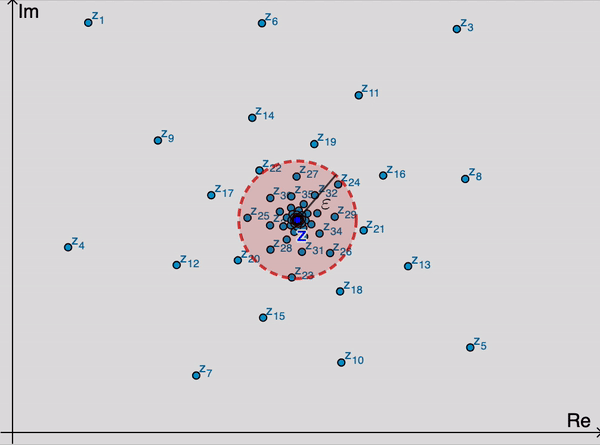
La secuencia\(\left\{z_n\right\}_{n=1}^{\infty}\) puede tener como máximo un límite. Es decir, un límite\(z\) es único si existe. Cuando ese límite existe, se dice que la secuencia converge a\(z\); y escribimos
\ (\ begin {eqnarray*}
\ lim_ {n\ rightarrow\ infty} z_n=z
\ end {eqnarray*}\)
Si la secuencia no tiene límite, diverge.
Teorema\(\PageIndex{1}\)
Supongamos que\(z_n=x_n+iy_n\left ( n=1,2,3,\ldots \right )\) y\(z=x+iy\). Entonces
\ (\ begin {eqnarray}\ label {teoseq01}
\ lim_ {n\ rightarrow\ infty} z_n=z
\ end {eqnarray}\)
si y solo si
\ (\ begin {eqnarray}\ label {teoseq02}
\ lim_ {n\ rightarrow\ infty} x_n=x\ quad\ text {y}\ quad\ lim_ {n\ rightarrow\ infty} y_n=y.
\ end {eqnarray}\)
- Prueba
-
Para probar este teorema, primero asumimos que las condiciones (3) se mantienen. Es decir, existen, para cada uno\(ε>0\), enteros positivos\(n_1\) y\(n_2\) tales que
\(|x_n-x|<\frac{\varepsilon}{2}\quad \text{whenever} \quad n>n_1\)
y\(|y_n-y|<\frac{\varepsilon}{2}\quad \text{whenever} \quad n>n_2.\)
De ahí\(n_0\) que si es el mayor de los dos enteros\(n_1\) y\(n_2\),\ (|x_n-x|<\ frac {\ varepsilon} {2}\ quad\ texto {y}\ quad |y_n-y|<\ frac {\ varepsilon} {2}\ quad
Desde
\ texto {siempre}\ quad n > n_0.\)\(|(x_n+iy_n)-(x+iy)|=|(x_n-x)+(y_n-y)|\leq |x_n-x|+|y_n-y|,\)
entonces\(|z_n-z|< \frac{\varepsilon}{2}+\frac{\varepsilon}{2} \quad \text{whenever} \quad n > n_0.\)
Por lo tanto la condición (2) se mantiene.Por el contrario, si empezamos con la condición (2), sabemos que para cada número positivo\(\varepsilon\), existe un entero positivo\(n_0\) tal que
\(|(x_n+iy_n)-(x+iy)|<\varepsilon \quad \text{whenever} \quad n>n_0.\)
Sin embargo\(|x_n-x|\leq |(x_n-x)+(y_n-y)|=|(x_n+iy_n)-(x+iy)|\)
y\(|y_n-y|\leq |(x_n-x)+(y_n-y)|=|(x_n+iy_n)-(x+iy)|.\)
Consecuentemente\ (|x_n-x|<\ varepsilon\ quad\ text {y}\ quad |y_n-y|<\ varepsilon\ quad\ texto {siempre}\ quad n
> n_0.\)Por lo tanto, se cumplen las condiciones (3). ■
Convergencia de Serie
Una serie infinita
\ (\ begin {eqnarray}\ label {series01}
\ suma_ {n=1} ^ {\ infty} z_n=z_1+z_2+z_3+\ cdots
\ end {eqnarray}\)
de números complejos converge a la suma\(S\) si la secuencia
\ (\ begin {eqnarray}\ label {suma parcial}
\ suma_ {n=1} ^ {N} z_n=z_1+z_2+z_3+\ cdots +z_n\ quad (N=1,2,3,\ ldots)
\ end {eqnarray}\)
de sumas parciales converge a\(S\); luego escribimos
\(\sum_{n=1}^{\infty}z_n=S.\)
Tenga en cuenta que como una secuencia puede tener como máximo un límite, una serie puede tener como máximo una suma. Cuando una serie no converge, decimos que diverge.
Teorema\(\PageIndex{2}\)
Supongamos que\(z_n=x_n+iy_n\left ( n=1,2,3,\ldots \right )\) y\(S=X+iY\). Entonces
\ (\ begin {eqnarray}\ label {teo01}
\ sum_ {n=1} ^ {\ infty} z_n=s
\ end {eqnarray}\)
si y solo si
\ (\ begin {eqnarray}\ label {teo02}
\ suma_ {n=1} ^ {\ infty} x_n=x\ quad\ texto {y}\ quad\ suma_ {n=1} ^ {\ infty} Y_n=y.
\ end {eqnarray}\)
- Prueba
-
Para probar este teorema, primero escribimos las sumas parciales (5) como
\ (\ begin {eqnarray}\ label {teo03}
donde
S_N = x_n+iy_n,
\ end {eqnarray}\)\(X_N = \sum_{n=1}^{N}x_n \quad \text{and}\quad Y_N = \sum_{n=1}^{N}y_n.\)
Ahora la declaración (6) es verdadera si y solo si\ (\ begin {eqnarray}\ label {teo04}
y, en vista de la relación (8) y el teorema 1 sobre las secuencias, limit (9) se mantiene si y solo si
\ lim_ {N\ rightarrow\ infty} S_N = S;
\ end {eqnarray}\)\ (\ begin {eqnarray}\ label {teo05}
\ lim_ {N\ rightarrow\ infty} X_N=X\ quad\ text {y}\ quad\ lim_ {N\ rightarrow\ infty} Y_N=Y.
\ end {eqnarray}\)Límites (10) por lo tanto implican declaración (6), y a la inversa. Dado que\(X_N=X\) y\(Y_N=Y\) son sumas parciales de la serie (7), se prueba el teorema. ■
Este teorema puede ser útil para demostrar que una serie de propiedades familiares de las series en el cálculo se trasladan a series cuyos términos son números complejos.
Propiedad 1: Si converge una serie de números complejos, el\(n\) -ésimo término converge a cero como\(n\) tiende al infinito.
De la Propiedad 1 se deduce que los términos de las series convergentes están acotados. Es decir, cuando la serie (4) converge, existe una constante positiva\(M\) tal que
\(|z_n| \leq M \; \text{ for each positive integer } n.\)
Otra propiedad importante de series de números complejos que se desprende de una propiedad correspondiente en cálculo es la siguiente.
Propiedad 2: La convergencia absoluta de una serie de números complejos implica la convergencia de esa serie.
Recordemos que la serie (4) se dice que es absolutamente convergente si la serie
\ (\ begin {eqnarray*}\ label {series02}
\ suma_ {n=1} ^ {\ infty} |z_n|=\ suma_ {n=1} ^ {\ infty}\ sqrt {x^2_n+y^2_n}\ quad\ quad (z_n=x_n+iy_n)
\ end {eqnarray*}\)
de números reales\(\sqrt{x^2_n+y^2_n}\) converge.
Para establecer el hecho de que la suma de una serie es un número dado\(S\), a menudo es conveniente definir el resto\(ρN\) después de\(N\) términos, utilizando las sumas parciales:
\ (\ begin {eqnarray*}\ label {series03}
\ rho_n=s-s_n
\ end {eqnarray*}\)
Por lo tanto\(S=S_N+\rho_N\). Ahora\(|S_N-S|=|\rho_N-0|\), desde entonces una serie converge a un número\(S\) si y sólo si la secuencia de restos tiende a cero.
Ejemplo\(\PageIndex{1}\)
Con la ayuda de restos, es fácil verificar que
\ (\ begin {eqnarray*}
\ sum_ {n=0} ^ {\ infty} z^n=\ frac {1} {1-z}\ quad\ text {siempre}\ quad |z|< 1
\ end {eqnarray*}\)
Solo necesitamos recordar la identidad
\(1+z+z^2+\cdots+z^n=\frac{1-z^{n+1}}{1-z}\)
escribir las sumas parciales
\ (\ begin {eqnarray}
S_N (z) =\ suma_ {n=0} ^ {\ infty} z^n=1+z+z^2+\ cdots+z^ {N-1}\ quad\ quad (z\ neq 1)
\ end {eqnarray}\)
como
\(S_N(z)=\frac{1-z^N}{1-z}.\)
Si
\(S(z)=\frac{1}{1-z}\)
entonces
\(\rho_N(z)=S(z)-S_N(z)=\frac{z^N}{1-z}\quad\quad(z\neq 1).\)
Por lo tanto
\(\left|\rho_N\right|=\frac{|z|^N}{|1-z|}\rightarrow 0\quad\text{only when}\quad |z|<1.\)
En este caso, es claro que los restos\(\rho_N\) tienden a cero cuando\(|z|<1\) pero no cuando\(|z|\geq 1\)
Exploración de series geométricas
La serie introducida en el ejemplo anterior
\ (\ begin {eqnarray*}
\ sum_ {n=0} ^ {\ infty} z^n=\ frac {1} {1-z}\ quad\ text {siempre}\ quad |z|< 1
\ end {eqnarray*}\)
se conoce como la serie geométrica.
Utilice el siguiente applet para explorar esta serie. Arrastre el punto\(z\) alrededor. Observe lo que sucede cuando está dentro, afuera o en el borde del círculo unitario. Arrastre el control deslizante para mostrar la suma parcial.
- Código
-
Ingresa el siguiente script en GeoGebra para explorarlo tú mismo y hacer tu propia versión. El símbolo # indica comentarios.
#Complex number Z = 0.72 + ί * 0.61 #Circle of radius 1 c = Circle((0,0), 1) #Number of terms of the partial series n = Slider(0, 250, 1, 1, 150, false, true, false, false) SetValue(n, 250) #Define the sequence z^n S = Join({0 + ί * 0, 1 + ί * 0}, Sequence(Z^j, j, 1, n)) #Define partial sum SP = Sequence(Sum(S, j), j, 1, n + 2) #Finally join the points of the partial sum L = Sequence(Segment(Element(SP, j), Element(SP, j + 1)), j, 1, n + 1)


