5.2: Serie Taylor

Para funciones reales

Dejar\(a\in \mathbb R\) y\(f(x)\) ser y función infinitamente diferenciable en un intervalo\(I\) que contiene\(a\). Entonces la serie unidimensional Taylor de\(f\) alrededor\(a\) viene dada por

\(f(x)=f(a)+f’(a)(x-a)+\frac{f’’(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots\)

que se puede escribir en la forma más compacta:

\(f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n.\)

Recordemos que, en análisis real, el teorema de Taylor da una aproximación de una función diferenciable de\(k\) tiempos alrededor de un punto dado por un polinomio Taylor de orden\(k\) -ésimo.

Por ejemplo, la mejor aproximación lineal para\(f(x)\) es

\(f(x)\approx f(a)+f′(a)(x−a).\)

Esta aproximación lineal se ajusta\(f(x)\) con una línea a través\(x=a\) que coincide con la pendiente de\(f\) at\(a\).

Para una mejor aproximación podemos agregar otros términos en la expansión. Por ejemplo, la mejor aproximación cuadrática es

\(f(x)\approx f(a)+f’(a)(x−a)+\frac12 f’’(a)(x−a)^2.\)

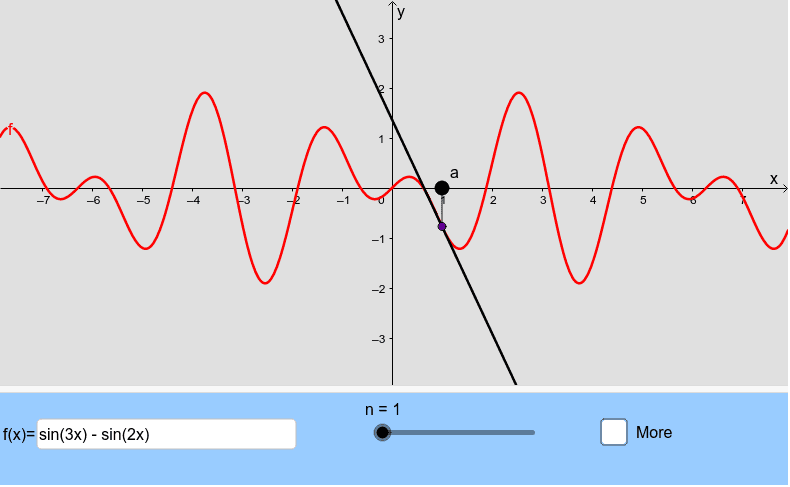
El siguiente applet muestra las sumas parciales de la serie Taylor para una función dada. Arrastre el control deslizante para mostrar más términos de la serie. Arrastre el punto a o cambie la función.

 

GRAFO INTERACTIVO

 

---

Para funciones complejas

Supongamos que una función\(f\) es analítica a lo largo de un disco\(|z -z_0|< R\), centrada en\(z_0\) y con el radio\(R_0\). Luego\(f(z)\) tiene la representación de la serie de potencia

\ (\ begin {eqnarray}\ label {seriefunction}
f (z) =\ suma_ {n=0} ^ {\ infty} a_n (z-z_0) ^n,\ quad |z-z_0|<r,
\ end {eqnarray}\)

donde

\ (\ begin {eqnarray}
a_n=\ frac {f^ {(n)} (z_0)} {n!} ,\ quad n=0,1,2,\ ldots
\ end {eqnarray}
\)

Es decir, la serie (1) converge a\(f(z)\) cuando\(z\) yace en el disco abierto declarado.

Cada serie de potencia compleja (1) tiene un radio de convergencia. Análogamente al concepto de intervalo de convergencia para series de potencia real, una serie de potencias complejas (1) tiene un círculo de convergencia, que es el círculo centrado en\(z_0\) el radio más grande\(R>0\) para el cual (1) converge en cada punto dentro del círculo\(|z−z_0|=R\). Una serie de poder converge absolutamente en todos los puntos\(z\) dentro de su círculo de convergencia, es decir, para todos\(z\) satisfactorios\(|z−z_0|<R\), y diverge en todos los puntos\(z\) exteriores al círculo, es decir, para todos\(z\) satisfactorios\(|z−z_0|>R\). El radio de convergencia puede ser:

1. \(R=0\)(en cuyo caso (1) converge sólo en su centro\(z=z_0\)),
2. \(R\)un número positivo finito (en cuyo caso (1) converge en todos los puntos interiores del círculo\(|z−z_0|<R\), o
3. \(R=∞\)(en cuyo caso (1) converge para todos\(z\)).

El radio de convergencia se puede calcular usando la prueba de relación de convergece. Por ejemplo, si:

1. \(\displaystyle \lim_{n\rightarrow \infty} \left| \frac{a_{n+1}}{a_n}\right| = L\neq 0\), el radio de convergencia es\(R=\dfrac{1}{L}\);
2. \(\displaystyle \lim_{n\rightarrow \infty}  \left| \frac{a_{n+1}}{a_n}\right|= 0\), el radio de convergencia es\(R=∞\);
3. \(\displaystyle \lim_{n\rightarrow \infty}  \left| \frac{a_{n+1}}{a_n}\right|= \infty\), el radio de convergencia es\(R=0\).

---

Exploración Dinámica

Utilice el siguiente applet para explorar las representaciones de la serie Taylor y su radio de convergencia que depende del valor de\(z_0\).

En el lado izquierdo del applet de abajo, se muestra un retrato de fase de una función compleja. En el lado derecho, se puede ver la aproximación de la función a través de sus polinomios Taylor en el punto base azul\(z_0\). Se puede modificar la función compleja\(z_0\), el punto base, el orden del polinomio (deslizador vertical) y el zoom (deslizador horizontal).

 

GRAFO INTERACTIVO

 

 

---

Serie Maclaurin

Una serie Taylor con centro\(z_0=0\)

\(f(z) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}z^n\)

se conoce como serie Maclaurin.

Algunas series importantes de Maclaurin son:

\ (\ begin {eqnarray*}
\ displaystyle\ frac {1} {1-z} &=&\ sum_ {n=0} ^ {\ infty} z^n,\ quad |z|\ lt 1;\\
\ displaystyle e^z &=&\ sum_ {n=0} ^ {\ infty}\ frac {z^n} {n!} \ quad |z|\ lt\ infty;\\
\ displaystyle\ sin z &=&\ sum_ {n=0} ^ {\ infty} (-1) ^n\ frac {z^ {2n+1}} {n!} \ quad |z|\ lt\ infty;\\
\ displaystyle\ cos z &=&\ sum_ {n=0} ^ {\ infty} (-1) ^n\ frac {z^ {2n}} {n!} \ quad |z|\ lt\ infty;\\
\ displaystyle\ sinh z &=&\ sum_ {n=0} ^ {\ infty}\ frac {z^ {2n+1}} {n!} \ quad |z|\ lt\ infty;\\
\ displaystyle\ cosh z &=&\ sum_ {n=0} ^ {\ infty}\ frac {z^ {2n}} {n!} \ quad |z|\ lt\ infty;
\ end {eqnarray*}\)

Ejercicio\(\PageIndex{1}\)

Ejercicio: Encuentra la expansión de la función en serie Maclaurin

\(f(z)=\frac{z}{z^4+9}\)

y calcular el radio de convergencia.

---

Nota

El applet fue originalmente escrito por Aaron Montag usando CindyJS. La fuente se puede encontrar en GitHub.