3.7: Semicontinuidad Inferior y Semicontinuidad Superior
- Page ID
- 107857
El concepto de semicontinuidad es conveniente para el estudio de máximos y mínimos de algunas funciones discontinuas.
Dejar\(f: D \rightarrow \mathbb{R}\) y dejar\(\bar{x} \in D\). Decimos que\(f\) es menor semicontinuo (l.s.c.) en\(\bar{x}\) si por cada\(\varepsilon > 0\), existe\(\delta > 0\) tal que
\[f(\bar{x})-\varepsilon<f(x) \text { for all } x \in B(\bar{x} ; \delta) \cap D .\]
Del mismo modo, decimos que\(f\) es semicontinuo superior (e.s.c.) en\(\bar{x}\) si por cada\(\varepsilon > 0\), existe\(\delta > 0\) tal que
\[f(x)<f(\bar{x})+\varepsilon \text { for all } x \in B(\bar{x} ; \delta) \cap D .\]
Está claro que\(f\) es continuo en\(\bar{x}\) si y sólo si\(f\) es semicontinuo inferior y semicontinuo superior en este punto.
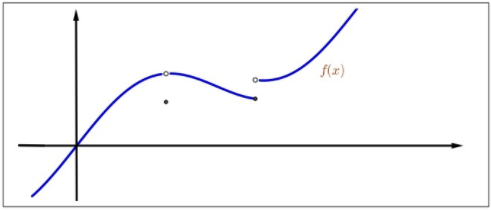
Figura\(3.6\): Semicontinuidad inferior.
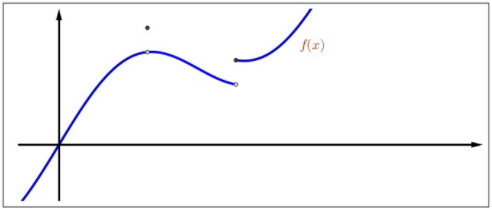
Figura\(3.7\): Semicontinuidad superior.
Dejar\(f: D \rightarrow \mathbb{R}\) y dejar\(\bar{x} \in D\) ser un punto límite de\(D\). Entonces\(f\) es menor semicontinuo en\(\bar{x}\) si y solo si
\[\liminf _{x \rightarrow \bar{x}} f(x) \geq f(\bar{x}) .\]
Del mismo modo,\(f\) es semicontinuo superior en\(\bar{x}\) si y solo si
\[\limsup _{x \rightarrow \bar{x}} f(x) \leq f(\bar{x}) .\]
- Prueba
-
Supongamos que\(f\) es menor semiconítono en\(\bar{x}\). Vamos\(\varepsilon > 0\). Entonces existe\(\delta_{0}>0\) tal que
\[f(\bar{x})-\varepsilon<f(x) \text { for all } x \in B\left(\bar{x} ; \delta_{0}\right) \cap D .\]
Esto implica
\[f(\bar{x})-\varepsilon \leq h\left(\delta_{0}\right),\]
donde
\[h(\delta)=\inf _{x \in B_{0}(\bar{x} ; \delta) \cap D} f(x) .\]
Por lo tanto,
\[\liminf _{x \rightarrow \bar{x}} f(x)=\sup _{\delta>0} h(\delta) \geq h\left(\delta_{0}\right) \geq f(\bar{x})-\varepsilon .\]
Ya que\(\varepsilon\) es arbitrario, obtenemos\(\liminf _{x \rightarrow \bar{x}} f(x) \geq f(\bar{x})\).
Ahora demostramos lo contrario. Supongamos
\[\liminf _{x \rightarrow \bar{x}} f(x)=\sup _{\delta>0} h(\delta) \geq f(\bar{x})\]
y vamos\(\varepsilon > 0\). Desde
\[\sup _{\delta>0} h(\delta)>f(\bar{x})-\varepsilon ,\]
existe\(\delta > 0\) tal que\(h(\delta)>f(\bar{x})-\varepsilon\). Esto implica
\[f(x)>f(\bar{x})-\varepsilon \text { for all } x \in B_{0}(\bar{x} ; \delta) \cap D .\]
Dado que esto también es cierto para\(x = \bar{x}\), la función\(f\) es menor semicontinua en\(\bar{x}\).
La prueba para la caja semicontinua superior es similar. \(\square\)
Dejar\(f: D \rightarrow \mathbb{R}\) y dejar\(\bar{x} \in D\). Entonces\(f\) es l.s.c. en\(\bar{x}\) si y sólo si por cada secuencia\(\left\{x_{k}\right\}\) en\(D\) que converge a\(\bar{x}\),
\[\liminf _{k \rightarrow \infty} f\left(x_{k}\right) \geq f(\bar{x}) .\]
Del mismo modo,\(f\) es u.s.c. en\(\bar{x}\) si y solo si por cada secuencia\(\left\{x_{k}\right\}\) en\(D\) que converge a\(\bar{x}\),
\[\limsup _{k \rightarrow \infty} f\left(x_{k}\right) \leq f(\bar{x}) .\]
- Prueba
-
Supongamos que\(f\) es l.s.c. en\(\bar{x}\). Entonces para cualquiera\(\varepsilon > 0\), existe\(\delta > 0\) tal que (3.12) sostiene. Ya que\(\left\{x_{k}\right\}\) converge a\(\bar{x}\), tenemos\(x_{k} \in B(\bar{x} ; \delta)\) cuando\(k\) es suficientemente grande. Por lo tanto,
\[f(\bar{x})-\varepsilon<f\left(x_{k}\right)\]
para tal\(k\). De ello se deduce que\(f(\bar{x})-\varepsilon \leq \liminf _{k \rightarrow \infty} f\left(x_{k}\right)\). Ya que\(\varepsilon\) es arbitrario, de ello se deduce que\(f(\bar{x}) \leq \liminf _{k \rightarrow \infty} f\left(x_{k}\right)\).
Ahora demostramos lo contrario. Supongamos\(\liminf _{k \rightarrow \infty} f\left(x_{k}\right) \geq f(\bar{x})\) y asumamos, a modo de contradicción, que no\(f\) es l.s.c. at\(\bar{x}\). Entonces existe\(\bar{\varepsilon}>0\) tal que para cada\(\delta > 0\), existe\(x_{\delta} \in B(\bar{x} ; \delta) \cap D\) con
\[f(\bar{x})-\bar{\varepsilon} \geq f\left(x_{\delta}\right) .\]
Aplicando esto para\(\delta_{k}=\frac{1}{k}\), obtenemos una secuencia\(\left\{x_{k}\right\}\) en la\(D\) que converge a\(\bar{x}\) con
\[f(\bar{x})-\bar{\varepsilon} \geq f\left(x_{k}\right) \text { for every } \mathrm{k} .\]
Esto implica
\[f(\bar{x})-\bar{\varepsilon} \geq \liminf _{k \rightarrow \infty} f\left(x_{k}\right) .\]
Esto es una contradicción. \(\square\)
Vamos\(f: D \rightarrow \mathbb{R}\). Decimos que\(f\) es menor semicontinuo en\(D\) (o menor semicontinuo si no se produce confusión) si es menor semicontinuo en cada punto de\(D\).
Supongamos que\(D\) es un conjunto compacto de\(\mathbb{R}\) y\(f: D \rightarrow \mathbb{R}\) es semicontinuo inferior. Entonces\(f\) tiene un mínimo absoluto encendido\(D\). Eso significa que existe\(\bar{x} \in D\) tal que
\[f(x) \geq f(\bar{x}) \text { for all } x \in D .\]
- Prueba
-
Primero probamos que\(f\) está acotado a continuación. Supongamos por contradicción que para cada\(k \in \mathbb{N}\), existe\(x_{k} \in D\) tal que
\[f\left(x_{k}\right)<-k .\]
Dado que\(D\) es compacto, existe una subsecuencia\(\left\{x_{k_{\ell}}\right\}\) de la\(\left\{x_{k}\right\}\) que converge a\(x_{0} \in D\). Dado que\(f\) es l.s.c., por Teorema 3.7.2
\[\liminf _{\ell \rightarrow \infty} f\left(x_{k_{\ell}}\right) \geq f\left(x_{0}\right) .\]
Esto es una contracción porque\(\liminf _{\ell \rightarrow \infty} f\left(x_{k_{\ell}}\right)=-\infty\). Estos espectáculos\(f\) se acotan a continuación. Definir
\[\gamma=\inf \{f(x): x \in D\} .\]
Dado que el conjunto no\(\{f(x): x \in D\}\) está vacío y delimitado por debajo,\(\gamma \in \mathbb{R}\).
Que\(\left\{u_{k}\right\}\) sea una secuencia en\(D\) tal que\(\left\{f\left(u_{k}\right)\right\}\) converja a\(\gamma\). Por la compacidad de\(D\), la secuencia\(\left\{u_{k}\right\}\) tiene una subsecuencia convergente\(\left\{u_{k_{\ell}}\right\}\) que converge a algunos\(\bar{x} \in D\). Entonces
\[\gamma=\lim _{\ell \rightarrow \infty} f\left(u_{k_{\ell}}\right)=\liminf _{\ell \rightarrow \infty} f\left(u_{k_{\ell}}\right) \geq f(\bar{x}) \geq \gamma .\]
Esto implica\(\gamma=f(\bar{x})\) y, por lo tanto,
\[f(x) \geq f(\bar{x}) \text { for all } x \in D .\]
La prueba ya está completa. \(\square\)
El siguiente teorema se demuestra de manera similar.
Supongamos que\(D\) es un subconjunto compacto de\(\mathbb{R}\) y\(f: D \rightarrow \mathbb{R}\) es semicontinuo superior. Entonces\(f\) tiene un máximo absoluto encendido\(D\). Es decir, existe\(\bar{x} \in D\) tal que
\[f(x) \leq f(\bar{x}) \text { for all } x \in D .\]
Para cada\(a \in \mathbb{R}\), defina
\[\mathscr{L}_{a}(f)=\{x \in D: f(x) \leq a\}\]
y
\[\mathscr{L}_{a}(f)=\{x \in D: f(x) \leq a\} .\]
- Prueba
-
Agrega prueba aquí y automáticamente se ocultará
Vamos\(f: D \rightarrow \mathbb{R}\). Entonces\(f\) es menor semicontinuo si y solo si\(\mathscr{L}_{a}(f)\) se cierra en\(D\) para cada\(a \in \mathbb{R}\). Del mismo modo,\(f\) es semicontinuo superior si y solo si\(\mathscr{U}_{a}(f)\) está cerrado en\(D\) para cada\(a \in \mathbb{R}\).
- Prueba
-
Supongamos que\(f\) es menor semicontinuo. Usando Corolario 2.6.10, vamos a demostrar que por cada secuencia\(\left\{x_{k}\right\}\) en\(\mathscr{L}_{a}(f)\) que converja a un punto\(\bar{x} \in D\), obtenemos\(\bar{x} \in \mathscr{L}_{a}(f)\). Por cada\(k\), ya que\(x_{k} \in \mathscr{L}_{a}(f)\),\(f\left(x_{k}\right) \leq a\).
Dado que\(f\) es menor semicontinuo en\(\bar{x}\),
\[f(\bar{x}) \leq \liminf _{k \rightarrow \infty} f\left(x_{k}\right) \leq a .\]
Así,\(\bar{x} \in \mathscr{L}_{a}(f)\). De ello se deduce que\(\mathscr{L}_{a}(f)\) está cerrado.
Ahora demostramos lo contrario. Arreglar cualquier\(\bar{x} \in D\) y\(\varepsilon > 0\). Luego el conjunto
\[G=\{x \in D: f(x)>f(\bar{x})-\varepsilon\}=D \backslash \mathscr{L}_{f(x)-\varepsilon(f)}\]
está abierto en\(D\) y\(\bar{x} \in G\). Así, existe\(\delta > 0\) tal que
\[B(\bar{x} ; \delta) \cap D \subset G .\]
De ello se deduce que
\[f(\bar{x})-\varepsilon<f(x) \text { for all } x \in B(\bar{x} ; \delta) \cap D .\]
Por lo tanto,\(f\) es menor semicontinua. La prueba para la caja semicontinua superior es similar. \(\square\)
Para cada\(a \in \mathbb{R}\), también definimos
\[L_{a}(f)=\{x \in D: f(x)<a\}\]
y
\[U_{a}(f)=\{x \in D: f(x)>a\} .\]
Vamos\(f: D \rightarrow \mathbb{R}\). Entonces\(f\) es menor semicontinuo si y sólo si\(U_{a}(f)\) está abierto en\(D\) para cada\(a \in \mathbb{R}\). Del mismo modo,\(f\) es semicontinuo superior si y solo si\(L_{a}(f)\) está abierto en\(D\) para cada\(a \in \mathbb{R}\).
- Prueba
-
Agrega prueba aquí y automáticamente se ocultará
Vamos\(f: D \rightarrow \mathbb{R}\). Entonces\(f\) es continuo si y solo si para cada uno\(a,b \in \mathbb{R}\) con\(a < b\). el conjunto
\[O_{a, b}=\{x \in D: a<f(x)<b\}=f^{-1}((a, b))\]
es una entrada abierta\(D\).
- Prueba
-
Supongamos que\(f\) es continuo. Luego\(f\) es semicontinuo inferior y semicontinuo superior. Arreglar\(a,b \in \mathbb{R}\) con\(a < b\). Entonces
\[O_{a, b}=L_{b} \cap U_{a} .\]
Por Teorema 3.7.6, el conjunto\(O_{a, b}\) está abierto ya que es la intersección de dos conjuntos abiertos\(L_{a}\) y\(U_{b}\).
Demostremos lo contrario. Solo mostraremos que\(f\) es semicontinua inferior ya que la prueba de semicontinuidad superior es simiilar. Para cada\(a \in \mathbb{R}\), tenemos
\[U_{a}(f)=\{x \in D: f(x)>a\}=\cup_{n \in \mathbb{N}} f^{-1}((a, a+n))\]
Así,\(U_{a}(f)\) está abierto en\(D\) ya que es una unión de conjuntos abiertos en\(D\). Por lo tanto,\(f\) es menor semicontinuo por Corolario 3.7.6. \(\square\)
Ejercicio\(\PageIndex{1}\)
Dejar\(f\) ser la función dada por
\ [f (x) =\ left\ {\ begin {array} {ll}
x^ {2}, &\ text {if} x\ neq 0\ text {;}\\
-1, &\ text {if} x=0\ text {.}
\ end {array}\ derecho.\]
Demostrar que\(f\) es menor semicontinuo.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{2}\)
Dejar\(f\) ser la función dada por
\ [f (x) =\ left\ {\ begin {array} {ll}
x^ {2}, &\ text {if} x\ neq 0\ text {;}\\
1, &\ text {if} x=0\ text {.}
\ end {array}\ derecho.\]
Demostrar que\(f\) es semicontinuo superior.
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{3}\)
Dejar\(f, g: D \rightarrow \mathbb{R}\) ser funciones semicontinuas inferiores y dejar que\(k > 0\) sea una constante. Demostrar que\(f + g\) y\(kf\) son funciones semicontinuas inferiores en\(D\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Ejercicio\(\PageIndex{4}\)
Dejar\(f: \mathbb{R} \rightarrow \mathbb{R}\) ser una función semicontinua inferior tal que
\[\lim _{x \rightarrow \infty} f(x)=\lim _{x \rightarrow-\infty} f(x)=\infty .\]
Demostrar que\(f\) tiene un mínimo absoluto en algunos\(x_{0} \in \mathbb{R}\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.


