5.1: Límites

Dejar\(A \subset \mathbb{R}\) y dejar\(x\) ser un punto límite de\(A .\) En lo siguiente, vamos a dejar\(S(A, x)\) denotar el conjunto de todas las secuencias convergentes\(\left\{x_{n}\right\}_{n \in I}\) tal que\(x_{n} \in A\)\(n \in I, x_{n} \neq x\) para todos para todos\(n \in I,\) y\(\lim _{n \rightarrow \infty} x_{n}=x .\) Vamos a dejar\(S^{+}(A, x)\) ser el subconjunto\(S(A, x)\) de secuencias \(\left\{x_{n}\right\}_{n \in I}\)para el cual\(x_{n}>x\) para todos\(n \in I\) y\(S^{-}(A, x)\) ser el subconjunto\(S(A, x)\) de secuencias\(\left\{x_{n}\right\}_{n \in I}\) para las cuales\(x_{n}<x\) para todos\(n \in I .\)

Definición

Vamos\(D \subset \mathbb{R}, f: D \rightarrow \mathbb{R}, L \in \mathbb{R},\) y supongamos que\(a\) es un punto límite de\(D .\) Decimos que\(a\) se\(L,\) denota el límite de\(f\) como\(x\) enfoques

\[\lim _{x \rightarrow a} f(x)=L ,\]

si por cada secuencia\(\left\{x_{n}\right\}_{n \in I} \in S(D, a)\),

\[\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L .\]

Si\(S^{+}(D, a) \neq \emptyset,\) decimos que se\(L,\) denota el límite desde el derecho de\(f\) como\(x\) enfoques\(a\)

\[\lim _{x \rightarrow a+} f(x)=L ,\]

si por cada secuencia\(\left\{x_{n}\right\}_{n \in I} \in S^{+}(D, a)\),

\[\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L ,\]

y, si\(S^{-}(D, a) \neq \emptyset,\) decimos el límite desde la izquierda de\(f\) como\(a\) se\(x\) acerca se\(L,\) denota

\[\lim _{x \rightarrow a-} f(x)=L ,\]

si por cada secuencia\(\left\{x_{n}\right\}_{n \in I} \in S^{-}(D, a)\),

\[\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L .\]

También podemos denotar

\[\lim _{x \rightarrow a} f(x)=L\]

por escrito

\[f(x) \rightarrow L \text { as } x \rightarrow a .\]

Del mismo modo, podemos denotar

\[\lim _{x \rightarrow a^{+}} f(x)=L\]

por escrito

\[f(x) \rightarrow L \text { as } x \downarrow a\]

y

\[\lim _{x \rightarrow a^{-}} f(x)=L\]

por escrito

\[f(x) \rightarrow L \text { as } x \uparrow a\]

También dejamos

\[f(a+)=\lim _{x \rightarrow a^{+}} f(x)\]

y

\[f(a-)=\lim _{x \rightarrow a^{-}} f(x).\]

Debe quedar claro que si\(\lim _{x \rightarrow a} f(x)=L\) y\(S^{+}(D, a) \neq \emptyset,\) entonces\(f(a+)=L\). Del mismo modo, si\(\lim _{x \rightarrow a} f(x)=L\) y\(S^{-}(D, a) \neq \emptyset,\) entonces\(f(a-)=L\).

Proposición\(\PageIndex{1}\)

Supongamos\(D \subset \mathbb{R}, f: D \rightarrow \mathbb{R},\) y\(a\) es un punto límite de\(D\). Si\(f(a-)=f(a+)=L,\) entonces\(\lim _{x \rightarrow a} f(x)=L\).

Prueba

Supongamos\(\left\{x_{n}\right\}_{n=m}^{\infty} \in S(D, a) .\) Let

\[J^{-}=\left\{n: n \in \mathbb{Z}, x_{n}<a\right\}\]

y

\[J^{+}=\left\{n: n \in \mathbb{Z}, x_{n}>a\right\}.\]

Supongamos que\(J^{-}\) está vacío o finito y deja que\(k=m-1\) si\(J^{-}=\emptyset\) y, de lo contrario, deje\(k\) ser el entero más grande en\(J^{-} .\) Entonces\(\left\{x_{n}\right\}_{n=k+1}^{\infty} \in S^{+}(D, a),\) y así

\[\lim _{n \rightarrow \infty} f\left(x_{n}\right)=f(a+)=L.\]

Un argumento similar muestra que si\(J^{+}\) está vacío o finito, entonces

\[\lim _{n \rightarrow \infty} f\left(x_{n}\right)=f(a-)=L.\]

Si ni\(J^{-}\) ni\(J^{+}\) es finito o vacío, entonces\(\left\{x_{n}\right\}_{n \in J}-\) y\(\left\{x_{n}\right\}_{n \in J}+\) son subsecuencias de\(\left\{x_{n}\right\}_{n=m}^{\infty}\) con\(\left\{x_{n}\right\}_{n \in J^{-}} \in S^{-}(D, a)\) y\(\left\{x_{n}\right\}_{n \in J+} \in S^{+}(D, a) .\) Por lo tanto, dado cualquiera\(\epsilon>0,\) podemos encontrar números enteros\(N\) y\(M\) tal que

\[\left|f\left(x_{n}\right)-L\right|<\epsilon\]

cuando\(n \in\left\{j: j \in J^{-}, j>N\right\}\) y

\[\left|f\left(x_{n}\right)-L\right|<\epsilon\]

siempre que\(n \in\left\{j: j \in J^{+}, j>M\right\} .\)\(P\) sea el más grande de\(N\) y\(M .\) Ya que\(J^{-} \cup J^{+}=\left\{j: j \in \mathbb{Z}^{+}, j \geq m\right\},\) se deduce que

\[\left|f\left(x_{n}\right)-L\right|<\epsilon\]

siempre que\(n>P .\) De ahí\(\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L,\) y así\(\lim _{x \rightarrow a} f(x)=L\). \(\quad\)Q.E.D.

Proposición\(\PageIndex{2}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D,\) y\(f: D \rightarrow \mathbb{R}\). Si\(\lim _{x \rightarrow a} f(x)=L\) y\(\alpha \in \mathbb{R},\) entonces

\[\lim _{x \rightarrow a} \alpha f(x)=\alpha L.\]

Prueba

Supongamos\(\left\{x_{n}\right\}_{n \in I} \in S(D, a) .\) Entonces

\[\lim _{n \rightarrow \infty} \alpha f\left(x_{n}\right)=\alpha \lim _{n \rightarrow \infty} f\left(x_{n}\right)=\alpha L.\]

De ahí\(\lim _{x \rightarrow a} \alpha f(x)=\alpha L\). \(\quad\)Q.E.D.

Proposición\(\PageIndex{3}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R},\) y\(g: D \rightarrow \mathbb{R} .\) Si\(\lim _{x \rightarrow a} f(x)=L\) y\(\lim _{x \rightarrow a} g(x)=M,\) luego

\[\lim _{x \rightarrow a}(f(x)+g(x))=L+M.\]

Prueba

Supongamos\(\left\{x_{n}\right\}_{n \in I} \in S(D, a) .\) Entonces

\[\lim _{n \rightarrow \infty}\left(f\left(x_{n}\right)+g\left(x_{n}\right)\right)=\lim _{n \rightarrow \infty} f\left(x_{n}\right)+\lim _{n \rightarrow \infty} g\left(x_{n}\right)=L+M.\]

De ahí\(\lim _{x \rightarrow a}(f(x)+g(x))=L+M\). \(\quad\)Q.E.D.

Proposición\(\PageIndex{4}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R},\) y\(g: D \rightarrow \mathbb{R} .\) Si\(\lim _{x \rightarrow a} f(x)=L\) y\(\lim _{x \rightarrow a} g(x)=M,\) luego

\[\lim _{x \rightarrow a} f(x) g(x)=L M.\]

Ejercicio\(\PageIndex{1}\)

Demostrar la proposición anterior.

Proposición\(\PageIndex{5}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R}\),\(g: D \rightarrow \mathbb{R},\) y\(g(x) \neq 0\) para todos\(x \in D .\) Si\(\lim _{x \rightarrow a} f(x)=L, \lim _{x \rightarrow a} g(x)=M,\) y\(M \neq 0,\) luego

\[\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\frac{L}{M}.\]

Ejercicio\(\PageIndex{2}\)

Demostrar la proposición anterior.

Proposición\(\PageIndex{6}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R},\) y\(f(x) \geq 0\) para todos\(x \in D .\) Si\(\lim _{x \rightarrow a} f(x)=L,\) entonces

\[\lim _{x \rightarrow a} \sqrt{f(x)}=\sqrt{L}.\]

Ejercicio\(\PageIndex{3}\)

Demostrar la proposición anterior.

Dado\(D \subset \mathbb{R}, f: D \rightarrow \mathbb{R},\) y\(A \subset D,\) dejamos

\[f(A)=\{y: y=f(x) \text { for some } x \in A\}.\]

En particular,\(f(D)\) denota el rango de\(f\).

Proposición\(\PageIndex{7}\)

Supongamos que\(D \subset \mathbb{R}, E \subset \mathbb{R}, a\) es un punto límite de\(D, g: D \rightarrow \mathbb{R}\),\(f: E \rightarrow \mathbb{R},\) y\(g(D) \subset E .\) Por otra parte, supongamos\(\lim _{x \rightarrow a} g(x)=b\) y, para algunos\(\epsilon>0\),\(g(x) \neq b\) para todos\(x \in(a-\epsilon, a+\epsilon) \cap D .\) Si\(\lim _{x \rightarrow b} f(x)=L,\) entonces

\[\lim _{x \rightarrow a} f \circ g(x)=L.\]

Prueba

Supongamos\(\left\{x_{n}\right\}_{n \in I} \in S(D, a) .\) Entonces

\[\lim _{n \rightarrow \infty} g\left(x_{n}\right)=b.\]

Que\(N \in \mathbb{Z}^{+}\) tal que\(\left|x_{n}-a\right|<\epsilon\) cada vez que\(n>N .\) Entonces

\[\left\{g\left(x_{n}\right)\right\}_{n=N+1}^{\infty} \in S(E, b),\]

por lo

\[\lim _{n \rightarrow \infty} f\left(g\left(x_{n}\right)\right)=L.\]

Así\(\lim _{x \rightarrow a} f \circ g(x)=L\). \(\quad\)Q.E.D.

Ejemplo\(\PageIndex{1}\)

Let

\[g(x)=\left\{\begin{array}{ll}{0,} & {\text { if } x \neq 0,} \\ {1,} & {\text { if } x=0.}\end{array}\right.\]

Si\(f(x)=g(x),\) entonces

\[f \circ g(x)=\left\{\begin{array}{ll}{1,} & {\text { if } x \neq 0,} \\ {0,} & {\text { if } x=0.}\end{array}\right.\]

De ahí\(\lim _{x \rightarrow 0} f \circ g(x)=1,\) aunque\(\lim _{x \rightarrow 0} g(x)=0\) y\(\lim _{x \rightarrow 0} f(x)=0\).

5.1.1 Límites de polinomios y funciones racionales

Ejemplo\(\PageIndex{2}\)

Si\(c \in \mathbb{R}\) y\(f: \mathbb{R} \rightarrow \mathbb{R}\) es dado por\(f(x)=c\) para todos\(x \in \mathbb{R}\), entonces claramente\(\lim _{x \rightarrow a} f(x)=c\) para cualquiera\(a \in \mathbb{R}\).

Ejemplo\(\PageIndex{3}\)

Supongamos que\(f: \mathbb{R} \rightarrow \mathbb{R}\) está definido por\(f(x)=x\) para todos\(x \in \mathbb{R} .\) Si, para cualquier\(a \in \mathbb{R},\left\{x_{n}\right\}_{n \in I} \in S(\mathbb{R}, a),\) entonces

\[\lim _{n \rightarrow \infty} f\left(x_{n}\right)=\lim _{n \rightarrow \infty} x_{n}=a.\]

De ahí\(\lim _{x \rightarrow a} x=a\).

Ejemplo\(\PageIndex{4}\)

Supongamos\(n \in \mathbb{Z}^{+}\) y\(f: \mathbb{R} \rightarrow \mathbb{R}\) está definido por\(f(x)=x^{n}\). Entonces

\[\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} x^{n}=\prod_{i=1}^{n} \lim _{x \rightarrow a} x=a^{n}.\]

Definición

Si\(n \in \mathbb{Z}, n \geq 0,\) y\(b_{0}, b_{1}, \ldots, b_{n}\) son números reales con\(b_{n} \neq 0,\) entonces llamamos a la función\(p: \mathbb{R} \rightarrow \mathbb{R}\) definida por

\[p(x)=b_{n} x^{n}+b_{n-1} x^{n-1}+\cdots+b_{1} x+b_{0}\]

un polinomio de grado\(n\).

Ejercicio\(\PageIndex{4}\)

Demostrar que si\(f\) es un polinomio y\(a \in \mathbb{R},\) luego\(\lim _{x \rightarrow a} f(x)=f(a)\).

Definición

Supongamos\(p\) y\(q\) son polinomios y

\[D=\{x: x \in \mathbb{R}, q(x) \neq 0\}.\]

Llamamos a la función\(r: D \rightarrow \mathbb{R}\) definida por

\[r(x)=\frac{p(x)}{q(x)}\]

una función racional.

Ejercicio\(\PageIndex{5}\)

Mostrar que si\(f\) es una función racional y\(a\) está en el dominio de\(f,\) entonces\(\lim _{x \rightarrow a} f(x)=f(a)\).

Ejercicio\(\PageIndex{6}\)

Supongamos que\(D \subset \mathbb{R}, a \in D\) es un punto límite de\(D,\) y\(\lim _{x \rightarrow a} f(x)=L\). Si\(E=D \backslash\{a\}\) y\(g: E \rightarrow \mathbb{R}\) está definido por\(g(x)=f(x)\) para todos\(x \in E,\) muestran que\(\lim _{x \rightarrow a} g(x)=L .\)

Ejercicio\(\PageIndex{7}\)

Evaluar

\[\lim _{x \rightarrow 1} \frac{x^{5}-1}{x^{3}-1}.\]

Ejercicio\(\PageIndex{8}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R}, g: D \rightarrow \mathbb{R}\),\(h: D \rightarrow \mathbb{R},\) y\(f(x) \leq h(x) \leq g(x)\) para todos\(x \in D .\) si\(\lim _{x \rightarrow a} f(x)=L\) y\(\lim _{x \rightarrow a} g(x)=L,\) mostrar que\(\lim _{x \rightarrow a} h(x)=L .\) (Este es el teorema squeeze para límites de funciones.)

Obsérvese que los resultados anteriores que se hayan señalado para los límites se mantendrán también para los límites unilaterales apropiados, es decir, límites desde la derecha o desde la izquierda.

Ejercicio\(\PageIndex{9}\)

Supongamos

\[f(x)=\left\{\begin{array}{ll}{x+1,} & {\text { if } x<0,} \\ {4,} & {\text { if } x=0,} \\ {x^{2},} & {\text { if } x>0.}\end{array}\right.\]

Evaluar\(f(0), f(0-),\) y\(f(0+) .\) ¿\(\lim _{x \rightarrow 0} f(x)\)Existe?

5.1.2 Definiciones equivalentes

Proposición\(\PageIndex{8}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D,\) y\(f: D \rightarrow \mathbb{R}\). Entonces\(\lim _{x \rightarrow a} f(x)=L\) si y solo si por cada\(\epsilon>0\) existe\(\delta>0\) tal que

\[|f(x)-L|<\epsilon \text { whenever } x \neq a \text { and } x \in(a-\delta, a+\delta) \cap D.\]

Prueba

\(\lim _{x \rightarrow a} f(x)=L .\)Supongamos que existe\(\epsilon>0\) tal que por cada\(\delta>0\) existe\(x \in(a-\delta, a+\delta) \cap D, x \neq a,\) para el cual existe\(|f(x)-L| \geq \epsilon\). Para\(n=1,2,3, \ldots,\) elegir

\[x_{n} \in\left(a-\frac{1}{n}, a+\frac{1}{n}\right) \cap D,\]

\(x_{n} \neq a,\)tal que\(\left|f\left(x_{n}\right)-L\right| \geq \epsilon .\) Entonces\(\left\{x_{n}\right\}_{n=1}^{\infty} \in S(D, a),\) pero\(\left\{f\left(x_{n}\right)\right\}_{n=1}^{\infty}\) no converge para\(L,\) contradecir la suposición de que\(\lim _{x \rightarrow a} f(x)=L\).

Ahora supongamos que por cada\(\epsilon>0\) existe\(\delta>0\) tal que\(|f(x)-L|<\epsilon\) cuando\(x \neq a\) y\(x \in(a-\delta, a+\delta) \cap D .\) Let\(\left\{x_{n}\right\}_{n \in I} \in S(D, a) .\) Given\(\epsilon>0\),\(\delta>0\) sea tal que\(|f(x)-L|<\epsilon\) cuando\(x \neq a\) y\(x \in(a-\delta, a+\delta) \cap D .\) Escoja\(N \in \mathbb{Z}\) tal que\(\left|x_{n}-a\right|<\delta\) siempre\(n>N .\) Entonces \(\left|f\left(x_{n}\right)-L\right|<\epsilon\)para todos\(n>N .\) De ahí\(\lim _{n \rightarrow \infty} f\left(x_{n}\right)=L,\) y así\(\lim _{x \rightarrow a} f(x)=L .\)\(\quad\) Q.E.D.

Las pruebas de las dos proposiciones siguientes son análogas.

Proposición\(\PageIndex{9}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R},\) y\(S^{-}(D, a) \neq \emptyset .\) Entonces\(\lim _{x \rightarrow a^{-}} f(x)=L\) si y solo si por cada\(\epsilon>0\) existe\(\delta>0\) tal que

\[|f(x)-L|<\epsilon \text { whenever } x \in(a-\delta, a) \cap D.\]

Proposición\(\PageIndex{10}\)

Supongamos que\(D \subset \mathbb{R}, a\) es un punto límite de\(D, f: D \rightarrow \mathbb{R},\) y\(S^{+}(D, a) \neq \emptyset .\) Entonces\(\lim _{x \rightarrow a^{+}} f(x)=L\) si y solo si por cada\(\epsilon>0\) existe\(\delta>0\) tal que

\[|f(x)-L|<\epsilon \text { whenever } x \in(a, a+\delta) \cap D.\]

5.1.3 Ejemplos

Ejemplo\(\PageIndex{5}\)

Definir\(f: \mathbb{R} \rightarrow \mathbb{R}\) por

\[f(x)=\left\{\begin{array}{ll}{1,} & {\text { if } x \text { is rational, }} \\ {0,} & {\text { if } x \text { is irrational. }}\end{array}\right.\]

Dejar\(a \in \mathbb{R} .\) Dado que cada intervalo abierto contiene números tanto racionales como irracionales, para cualquier\(\delta>0\) y cualquier elección de\(L \in \mathbb{R},\) allí existirá\(x \in(a-\delta, a+\delta),\)\(x \neq a,\) tal que

\[|f(x)-L| \geq \frac{1}{2}.\]

De ahí\(\lim _{x \rightarrow a} f(x)\) que no exista para ningún número real\(a\).

Ejemplo\(\PageIndex{6}\)

Definir\(f: \mathbb{R} \rightarrow \mathbb{R}\) por

\[f(x)=\left\{\begin{array}{ll}{x,} & {\text { if } x \text { is rational, }} \\ {0,} & {\text { if } x \text { is irrational. }}\end{array}\right.\]

Entonces\(\lim _{x \rightarrow 0} f(x)=0\) desde, dado\(\epsilon>0,|f(x)|<\epsilon\) siempre\(|x|<\epsilon\).

Ejercicio\(\PageIndex{9}\)

Mostrar que si\(f\) es como se da en el ejemplo anterior y\(a \neq 0\), entonces\(\lim _{x \rightarrow a} f(x)\) no existe.

Ejercicio\(\PageIndex{11}\)

Definir\(f: \mathbb{R} \rightarrow \mathbb{R}\) por

\[f(x)=\left\{\begin{array}{ll}{\frac{1}{q},} & {\text { if } x \text { is rational and } x=\frac{p}{q},} \\ {0,} & {\text { if } x \text { is irrational, }}\end{array}\right.\]

donde\(p\) y\(q\) se toman para ser números enteros relativamente primos con\(q>0,\) y tomamos\(q=1\) cuando\(x=0 .\) Mostrar eso, para cualquier número real\(a, \lim _{x \rightarrow a} f(x)=0\).

Ejemplo\(\PageIndex{7}\)

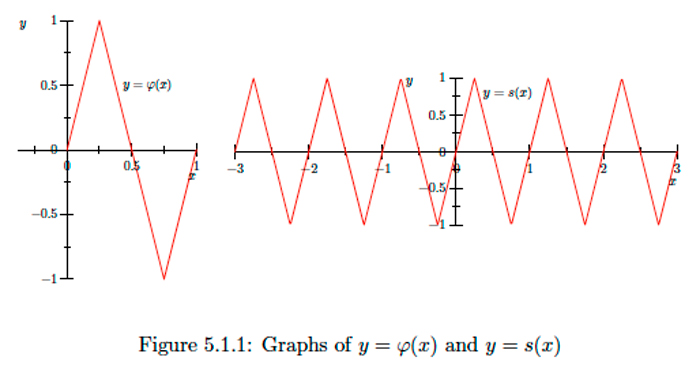
Definir\(\varphi:[0,1] \rightarrow[-1,1]\) por

\[\varphi(x)=\left\{\begin{array}{ll}{4 x,} & {\text { if } 0 \leq x \leq \frac{1}{4},} \\ {2-4 x,} & {\text { if } \frac{1}{4}<x<\frac{3}{4},} \\ {4 x-4,} & {\text { if } \frac{3}{4} \leq x \leq 1.}\end{array}\right.\]

Siguiente definir\(s: \mathbb{R} \rightarrow \mathbb{R}\) por\(s(x)=\varphi(x-\lfloor x\rfloor),\) donde\(\lfloor x\rfloor\) denota el entero más grande menor que o igual a\(x\) (es decir,\(\lfloor x\rfloor\) es el piso de\(x\)). La función\(s\) es un ejemplo de una función de diente de sierra. Ver las gráficas de\(\varphi\) y\(s\) en la Figura\(5.1 .1 .\) Tenga en cuenta que para cualquier\(n \in \mathbb{Z}\),

\[s([n, n+1])=[-1,1].\]

Ahora vamos\(D=\mathbb{R} \backslash\{0\}\) y definamos\(\sigma: D \rightarrow \mathbb{R}\) por

\[\sigma(x)=s\left(\frac{1}{x}\right).\]

Ver la gráfica de\(\sigma\) en la Figura\(5.1 .2 .\) Tenga en cuenta que para cualquier\(n \in \mathbb{Z}^{+}\),

\[\sigma\left(\left[\frac{1}{n+1}, \frac{1}{n}\right]\right)=s([n, n+1])=[-1,1].\]

De ahí que para cualquier\(\epsilon>0, \sigma((0, \epsilon))=[-1,1],\) y así\(\lim _{x \rightarrow 0^{+}} \sigma(x)\) no existe. De igual manera,\(\lim _{x \rightarrow 0^{-}} \sigma(x)\) ni tampoco\(\lim _{x \rightarrow 0} \sigma(x)\) existen.

Ejemplo\(\PageIndex{8}\)

Dejar\(s\) ser la función de diente de sierra del ejemplo anterior y dejar\(D=\mathbb{R} \backslash\{0\} .\) Definir\(\psi: D \rightarrow \mathbb{R}\) por

\[\psi(x)=x s\left(\frac{1}{x}\right).\]

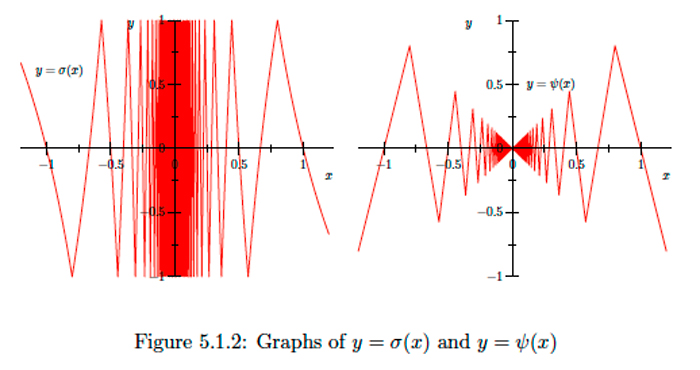
Ver Figura 5.1 .2 para la gráfica de\(\psi .\) Entonces para todos\(x \in D\),

\[-|x| \leq \psi(x) \leq|x|,\]

y así\(\lim _{x \rightarrow 0} \psi(x)=0\) por el teorema squeeze.

Definición

Vamos\(D \subset \mathbb{R}\) y\(f: D \rightarrow \mathbb{R} .\) Decimos\(f\) está acotado si existe un número real\(B\) tal que\(|f(x)| \leq B\) para todos\(x \in D\).

Ejercicio\(\PageIndex{12}\)

Supongamos que\(f: \mathbb{R} \rightarrow \mathbb{R}\) está acotado. \(\lim _{x \rightarrow 0} x f(x)=0\)Demuéstralo.